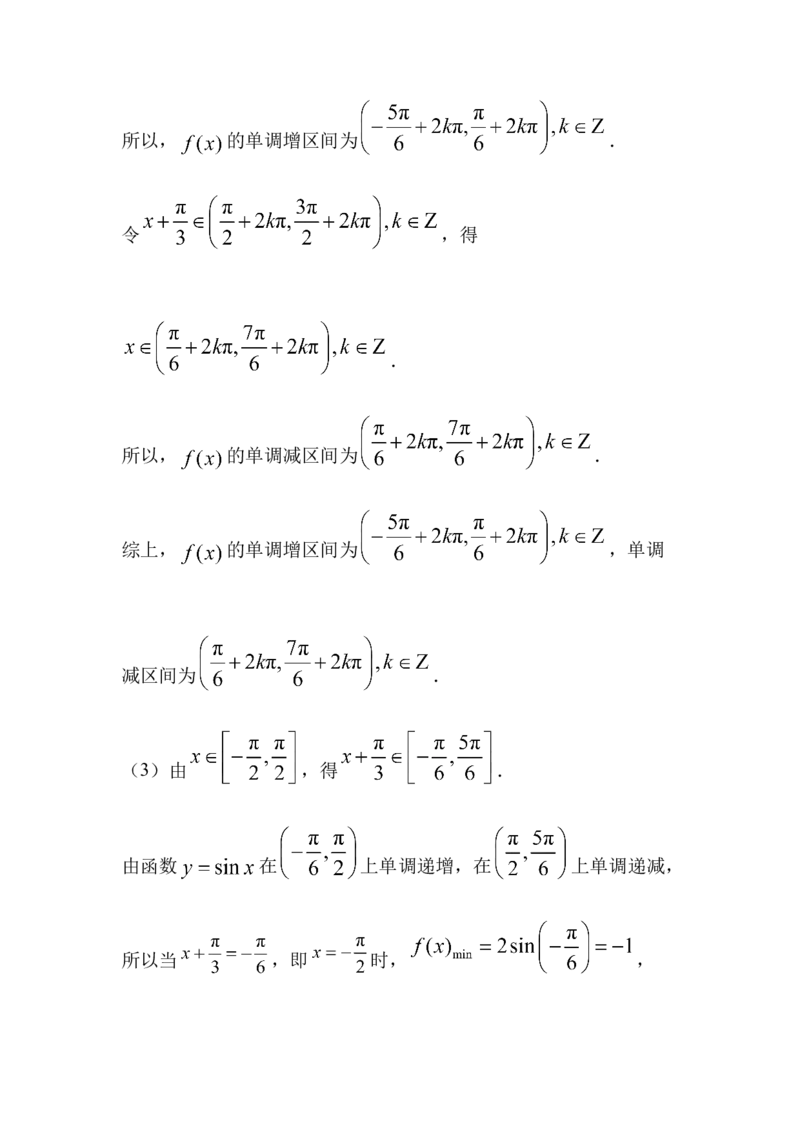文档内容
2025 年 3 月高一月考数学试卷
一、单选题
1. 的终边在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.下列函数是偶函数的是( )
A. B.
C. D.
3.tan585°=( )
A.− B.− C. D.
4.已知圆心角为 的扇形的半径为2,则该扇形的面积为( )
A. B. C. D.
5.在下列四个函数中,以 为最小正周期,且在区间 上单调递减的
是( )
A. B. C. D.
6. 的值为( )
A. B. C. D.
7. 的值为( )A. B. C. D.1
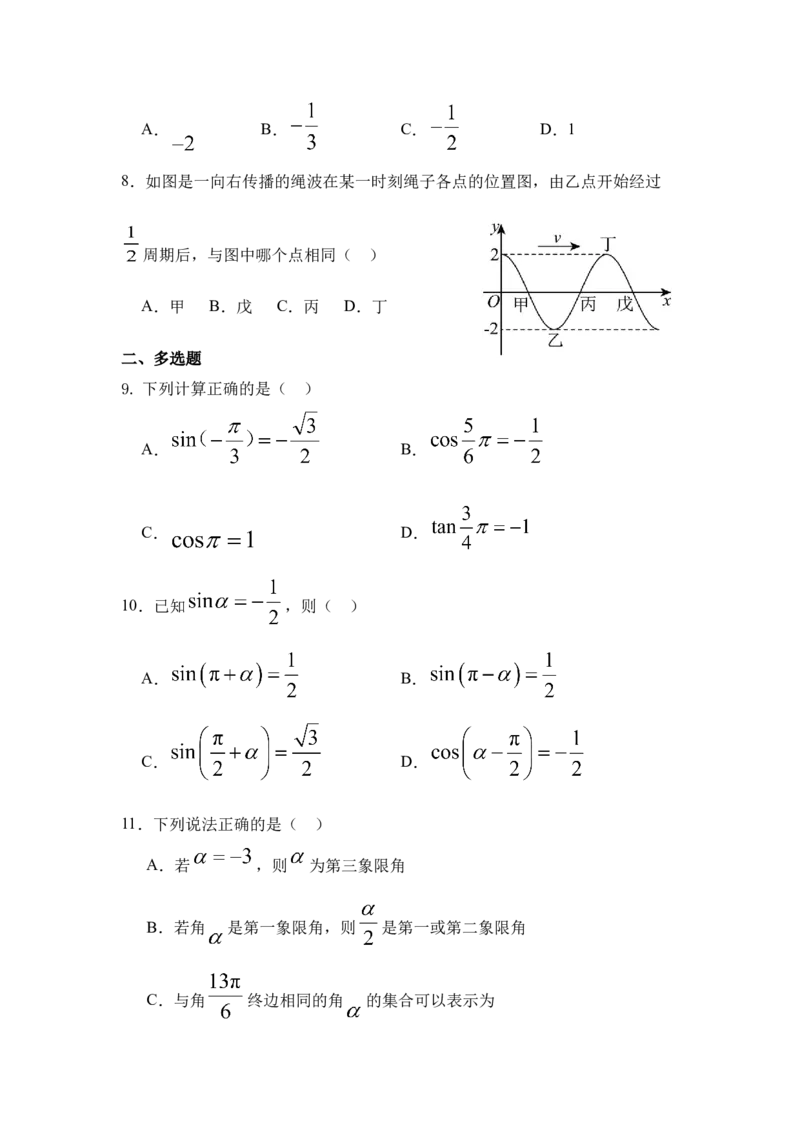
8.如图是一向右传播的绳波在某一时刻绳子各点的位置图,由乙点开始经过
周期后,与图中哪个点相同( )
A.甲 B.戊 C.丙 D.丁
二、多选题
9. 下列计算正确的是( )
A. B.
C. D.
10.已知 ,则( )
A. B.
C. D.
11.下列说法正确的是( )
A.若 ,则 为第三象限角
B.若角 是第一象限角,则 是第一或第二象限角
C.与角 终边相同的角 的集合可以表示为D.小于 的角一定是锐角
三、填空题
12.已知 , ,则 = .
13.已知 ,则 .
14.化简: .
四、解答题
15.(1) 为 的内角,已知 ,求 , 的值;
(2)已知 ,求 的值.
16.已知角 的顶点与原点 重合,始边与 轴的非负半轴重合,它的终边
过点 .(1)求 的值;
(2)若钝角 满足 ,求 的值.
17.设函数 , .
(1)解方程: ;
(2)求 的单调区间;
(3)求 在区间 上的值域.
18.已知函数 ,
(1)用五点法在平面直角坐标系中画出 在 上的图像;
(2)求函数 的值域;
(3)求不等式 的解集.
19.已知函数 .
(1)求 的定义域和最小正周期.
(2)求 的对称中心.《2025年3月3日高中数学作业》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B C B A C D D AD AC
11.AC
12. /
13.
14.
15.(1) , (2)
16.(1)
(2)
17.(1) 或
(2)单调减区间为 ,单调增区间为
(3)【详解】(1)由 ,即得 ,
从而 或者 ,解得 或者
,
所以方程 的解集为 或 .
(2)因为 关于 在 上单调递增,
在 上单调递减, 关于 在 上单调
递增.
令 ,得
.所以, 的单调增区间为 .
令 ,得
.
所以, 的单调减区间为 .
综上, 的单调增区间为 ,单调
减区间为 .
(3)由 ,得 .
由函数 在 上单调递增,在 上单调递减,
所以当 ,即 时, ,当 ,即 时, ,
因此, 在区间 的值域为 .
18.
【详解】(1)由函数 ,可得完成表格如下:
0
1 0 0 1
可得 在 的大致图象:如下图
(2)由 ,可得 得值域为 .
(3)由 ,可得 ,即
,当 时,由 ,得
.又由函数 的最小正周期为 ,
所以原不等式的解集为 .
19.(1)定义域为 ,最小正周期是 ;
(2)
【详解】(1) 函数 , ,
,
即 , ,
的定义域为 ,
, 的最小正周期是 ;
(2)令 , ,解得 , ,
此时 ;
函数 的对称中心为 .