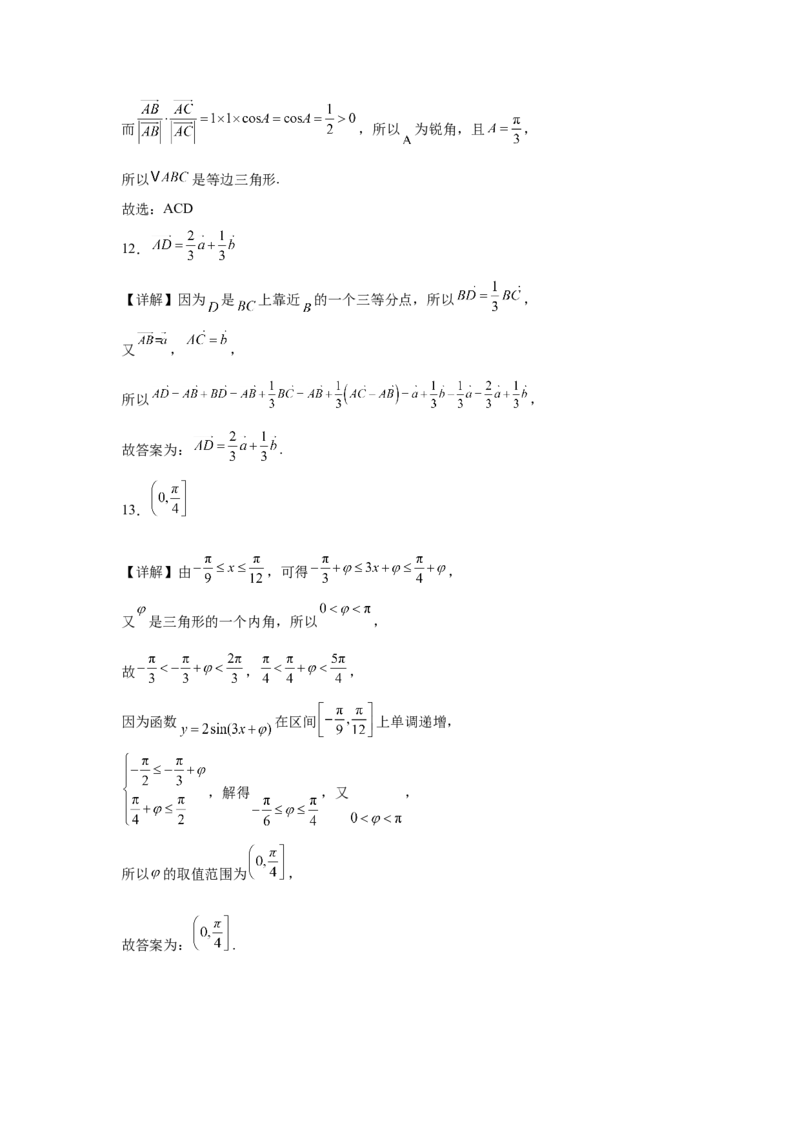文档内容
河南省信阳市2024-2025学年高一下学期4月期中数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知 是虚数单位, ( )
A. B. C. D.
2. 的值等于( )
A. B.1 C.0 D.
3.已知向量 , 的夹角为 ,且 ,则 在 上的投影向量为( )
A. B. C. D.
4.函数 , 的单调递增区间是( )
A. B.
C. 和 D. 和
5.已知向量 , 满足 , ,且 ,则 ( )
A. B.4 C.5 D.
6.已知函数 ,则下列说法错误的是( )
A.函数 的最小正周期为B.函数 的定义域为
C.函数 的图象的对称中心为 ,
D.函数 的单调递增区间为 ,
7.将函数 图象上所有点的横坐标缩小为原来的 (纵坐标不变),
再将所得曲线上所有的点向左平移 个单位长度,得到函数 的图象,若 的
图象关于 轴对称,则 的最小值是( )
A. B. C. D.
8.在 中,角 , , 的对边分别为 , , ,且面积为 .若
, ,则角 等于( )
A. B. C. D.
二、多选题
9.已知 是虚数单位,复数 ,则下列说法正确的是( )
A.复数 的虚部为 B.
C. D. 在复平面内对应的点在第二象限
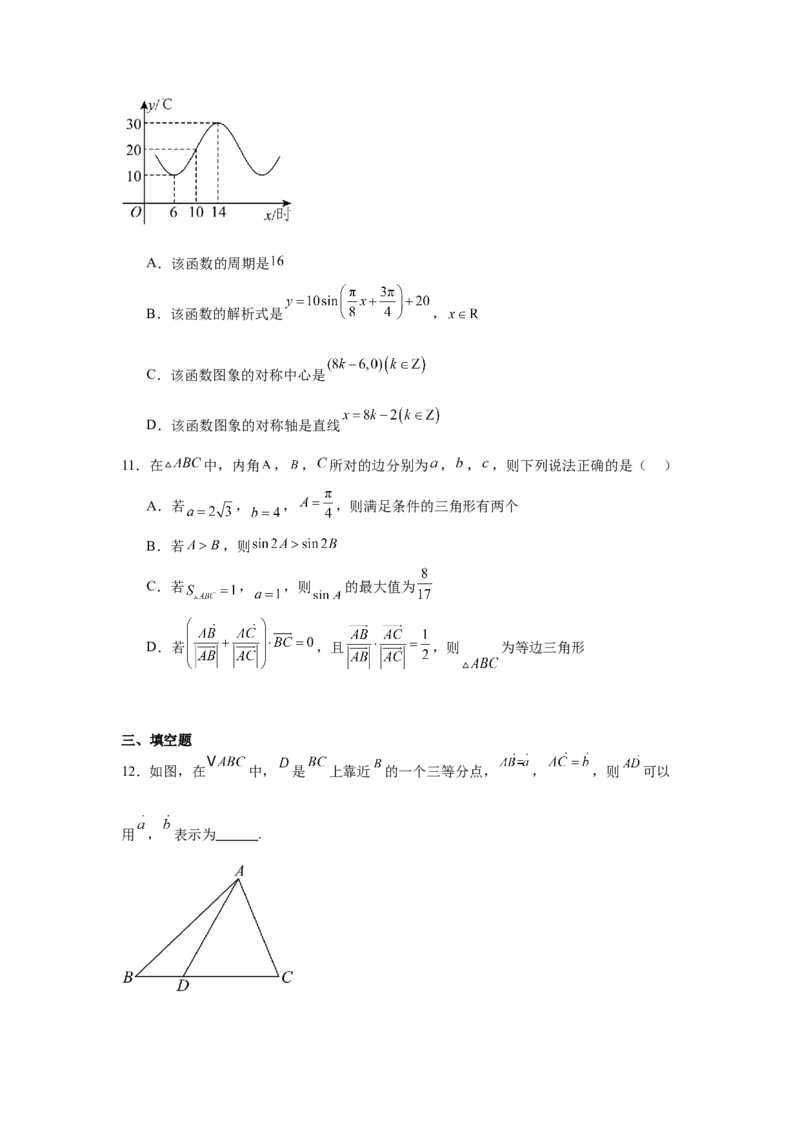
10.信阳是中国十佳宜居城市之一,气候宜人,环境优美.如图是信阳市夏季某一天的温度
变化曲线,若该曲线近似地满足函数 , 的部分图象,则下
列说法正确的是( )A.该函数的周期是
B.该函数的解析式是 ,
C.该函数图象的对称中心是
D.该函数图象的对称轴是直线
11.在 中,内角 , , 所对的边分别为 , , ,则下列说法正确的是( )
A.若 , , ,则满足条件的三角形有两个
B.若 ,则
C.若 , ,则 的最大值为
D.若 ,且 ,则 为等边三角形
三、填空题
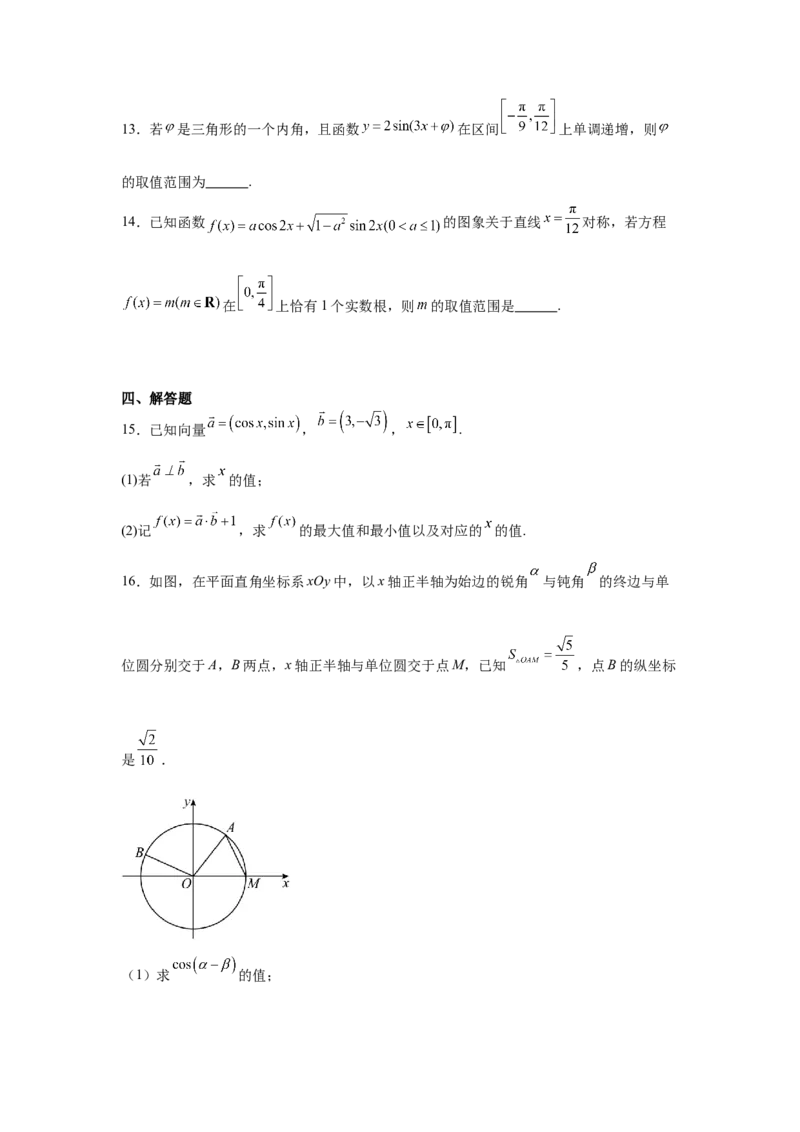
12.如图,在 中, 是 上靠近 的一个三等分点, , ,则 可以
用 , 表示为 .13.若 是三角形的一个内角,且函数 在区间 上单调递增,则
的取值范围为 .
14.已知函数 的图象关于直线 对称,若方程
在 上恰有1个实数根,则 的取值范围是 .
四、解答题
15.已知向量 , , .
(1)若 ,求 的值;
(2)记 ,求 的最大值和最小值以及对应的 的值.
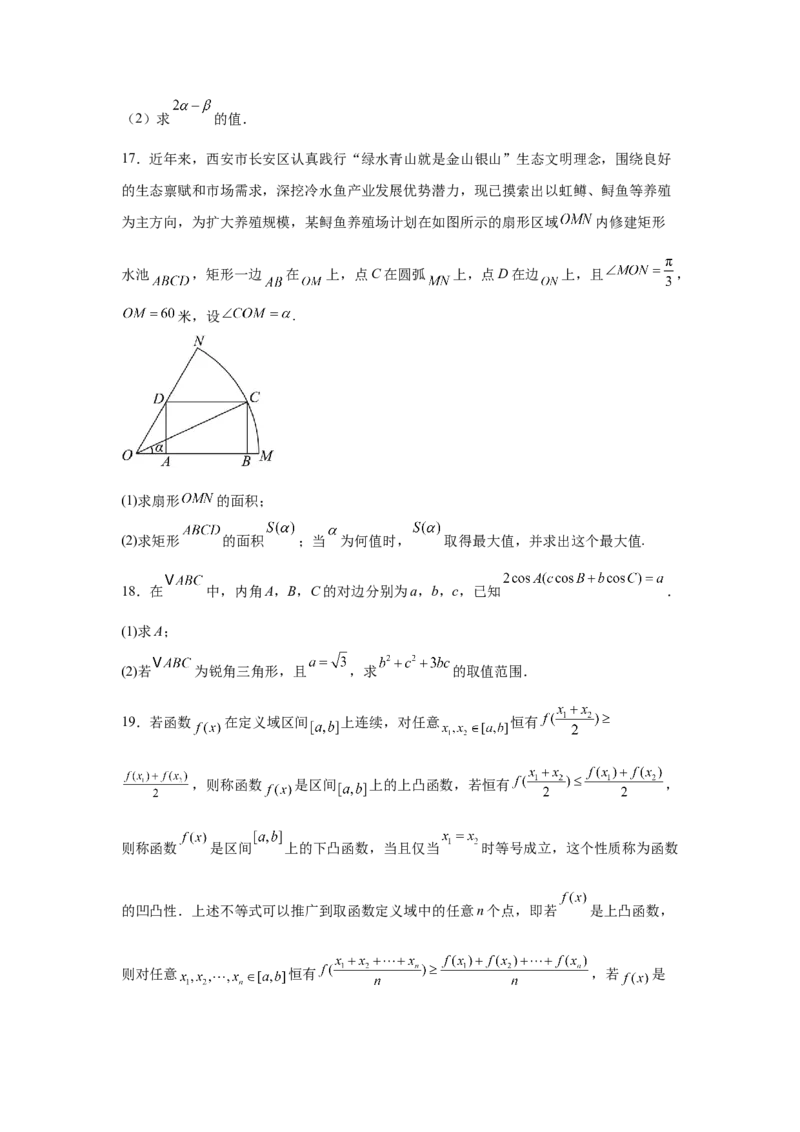
16.如图,在平面直角坐标系xOy中,以x轴正半轴为始边的锐角 与钝角 的终边与单
位圆分别交于A,B两点,x轴正半轴与单位圆交于点M,已知 ,点B的纵坐标
是 .
(1)求 的值;(2)求 的值.
17.近年来,西安市长安区认真践行“绿水青山就是金山银山”生态文明理念,围绕良好
的生态禀赋和市场需求,深挖冷水鱼产业发展优势潜力,现已摸索出以虹鳟、鲟鱼等养殖
为主方向,为扩大养殖规模,某鲟鱼养殖场计划在如图所示的扇形区域 内修建矩形
水池 ,矩形一边 在 上,点C在圆弧 上,点D在边 上,且 ,
米,设 .
(1)求扇形 的面积;
(2)求矩形 的面积 ;当 为何值时, 取得最大值,并求出这个最大值.
18.在 中,内角A,B,C的对边分别为a,b,c,已知 .
(1)求A;
(2)若 为锐角三角形,且 ,求 的取值范围.
19.若函数 在定义域区间 上连续,对任意 恒有
,则称函数 是区间 上的上凸函数,若恒有 ,
则称函数 是区间 上的下凸函数,当且仅当 时等号成立,这个性质称为函数
的凹凸性.上述不等式可以推广到取函数定义域中的任意n个点,即若 是上凸函数,
则对任意 恒有 ,若 是下凸函数,则对任意 恒有 ,
当且仅当 时等号成立.应用以上知识解决下列问题:
(1)判断函数 ( , ), , 在定义域上是上凸
函数还是下凸函数;(只写出结论,不需证明)
(2)利用(1)中的结论,在 中,求 的最大值;
(3)证明函数 是上凸函数.河南省信阳市2024-2025学年高一下学期4月期中数学试题参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B A C A C A D BC ABD
题号 11
答案 ACD
1.C
【详解】 ,
故选:C.
2.B
【详解】 ,
故选:B.
3.A
【详解】 在 上的投影向量为 .
故选:A
4.C
【详解】 ,
令 ,
函数 的单调递减区间为 .
由 ,
得 ,
而 ,所以所求单调递增区间是 和 .
故选:C.
5.A【详解】因为 , , ,
所以 ,则 ,故 ,
所以 ,则 .
故选:A.
6.C
【详解】对于A,函数 的最小正周期 ,A正确;
对于B,由 , ,得 , ,
所以函数 的定义域为 ,B正确;
对于C,由 , ,得 , ,
所以函数 的对称中心为 , ,C错误;
对于D,由 , ,得 , ,
所以函数 的单调递增区间为 , ,D正确.
故选:C
7.A
【详解】 可化为 ,
所以 ,
由条件可得 ,因为函数 的图象关于 轴对称,所以函数 为偶函数,
所以 , ,
所以 , ,又 ,
所以 的最小值为 ,
故选:A.
8.D
【详解】因为 ,
所以由正弦定理得 ,
所以 ,
因为 ,所以 ,
因为 ,所以 ,
因为 ,
所以 ,
因为 ,
所以 ,
所以 ,
故选:D
9.BC
【详解】因为 ,
所以复数 的虚部为 ,A错误;
因为 ,所以 ,B正确,
因为 ,所以 ,C正确;复数 在复平面内对应的点的坐标为 ,该点位于复平面的第一象限内,D错误;
故选:BC.
10.ABD
【详解】对于A选项,由图象可知,该函数的最小正周期为 ,A选项正
确;
对于B选项,由图象可得 ,解得 ,
,
图象经过点 ,
,
.
, ,则 , ,
所以,函数解析式为 , ,B选项正确;
对于C选项,令 , ,可得 , ,
所以函数 图象的对称中心为 ,C选项错误;
对于D选项,令 , ,可得 , ,
所以函数 图象的对称轴是直线 ,故D选项正确.
故选:ABD.
11.ACD【详解】A选项,若 , , ,
则 ,所以 ,
所以满足条件的三角形有两个,所以A选项正确.
B选项,若 ,如 , , , ,
则 , ,故 ,所以B选项错误.
C选项, , ,
余弦定理得 ,故
,
即 ,当且仅当 时等号成立,
由于三角形中, ,所以 ,
则 ,又 ,
即 ,整理得 ,
记得 ,所以 的最大值为 ,所以C选项正确.
D选项, 表示 方向的单位向量; 表示 方向的单位向量,
根据平面向量加法的几何意义可知 与 的角平分线共线,
由 可知 的角平分线与 垂直,
所以三角形 是等腰三角形.而 ,所以 为锐角,且 ,
所以 是等边三角形.
故选:ACD
12.
【详解】因为 是 上靠近 的一个三等分点,所以 ,
又 , ,
所以 ,
故答案为: .
13.
【详解】由 ,可得 ,
又 是三角形的一个内角,所以 ,
故 , ,
因为函数 在区间 上单调递增,
,解得 ,又 ,
所以 的取值范围为 ,
故答案为: .14.
【详解】因为 ,其中 ,
又函数 的图像关于直线 对称,且 ,
所以 ,解得 ,
所以 ,
当 时,令 ,
因为方程 在 上恰有1个实数根,且函数 在 上单调递
增,在 上单调递减,
,
所以 .
故答案为:
15.(1)
(2) 时, 的最大值为4; 时, 的最小值为
【详解】(1)因为 , , ,所以 .
若 ,则 ,与 矛盾,
故 ,于是 .又 ,
所以 .
(2)
.
因为 ,所以 ,从而 .
所以 ,
于是,当 ,即 时, 取到最大值 ;
当 ,即 时, 取到最小值 .
16.(1) ;(2) .
【详解】解:(1)由题意, .
, 为锐角,
, .
又点B的纵坐标是 且 为钝角,
, ..
(2) ,
,
, , .
又 ,
故 .
17.(1) 平方米;
(2) ,当 时, 取得最大值 平
方米.
【详解】(1)依题意, ,扇形半径即 米,
则扇形OMN的面积为 平方米.
(2)在 中, , ,
在 中, ,则 ,
于是 ,
则矩形 面积, ,
所以 ;
由 ,得 ,则当 时,即 时, ,
所以当 时, 取得最大值,最大值为 平方米.
18.(1)
(2)
【详解】(1)根据题意,由正弦定理得
,
又在 中,有 ,所以 ,
所以 ,所以 .
(2)结合(1)可得 , ,
由 ,则根据正弦定理有 ,得 , ,
根据余弦定理有 ,得 ,
所以
,
又 为锐角三角形,则有 , ,得 ,所以 ,所以 ,
故 .
19.(1)答案见解析;
(2) ;
(3)证明见解析.
【详解】(1)函数 , , ,
,
当 时, , 是下凸函数;
当 时, , 是上凸函数,
,
,显然 ,则 ,
因此 ,函数 是上凸函数.
(2)由(1)知函数 , 是上凸函数,
在 中, ,
即 ,当且仅当 取等号,
所以 的最大值是 .(3)函数 的定义域是 ,
要证函数 是上凸函数,即证 , ,
因为
= ,
显然 ,则 ,
而 ,即 ,则 ,
又 ,有 ,则 , ,