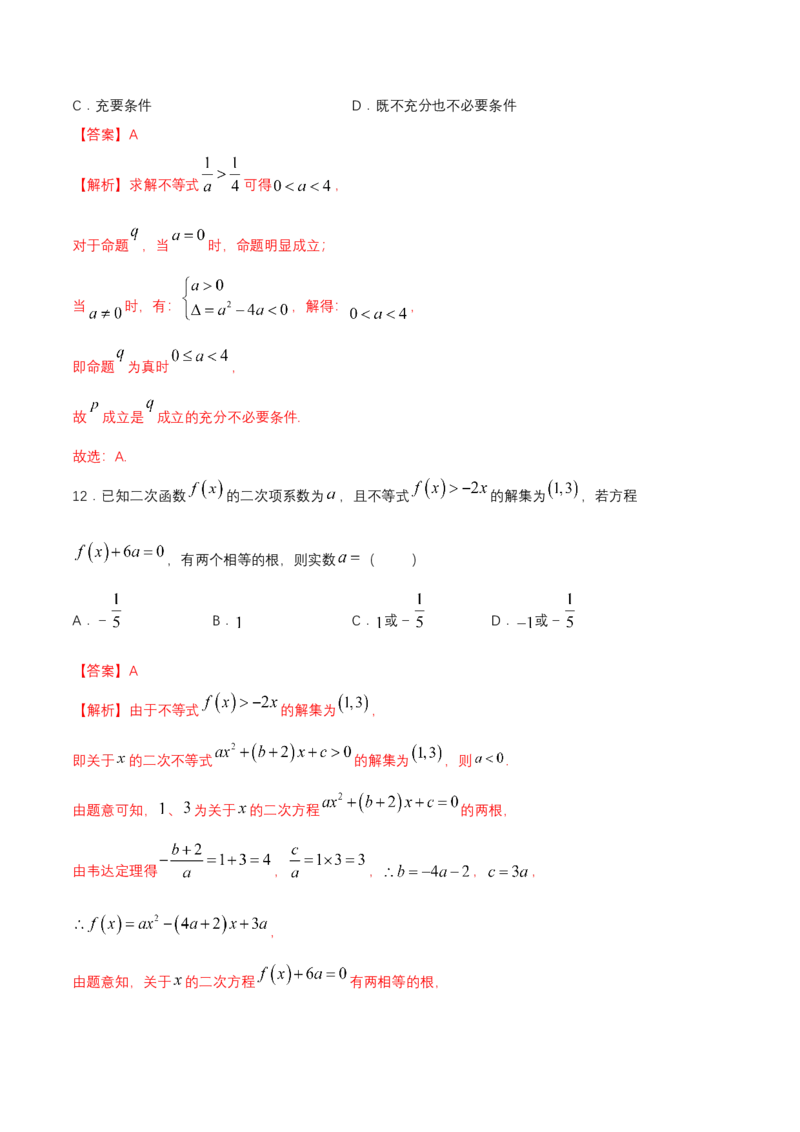文档内容
第二章 一元二次函数、方程和不等式
总分:120分时间:120分钟
一、单选题(总分48分,每题4分)
1.不等式 的解集为
A. B.
1
−
C. 2 或 D. 或
【答案】A
【解析】根据二次函数 的图象可知,不等式的解是 ,故选A.
2.已知正数 满足 ,则 的最小值是 ( )
A. B. C. D.
【答案】C
【解析】因为 ,所以 ,当且仅当 时,等号
成立,所以 的最小值为 .
故答案为:C.
3.若 且 ,则下列不等式成立的是( )
A. B. C. D.
【答案】D
【解析】选项A: ,符合 ,但不等式 不成立,故本选项是错误的;
选项B:当 符合已知条件,但零没有倒数,故 不成立 ,故本选项是错误的;
选项C:当 时, 不成立,故本选项是错误的;选项D:因为 ,所以根据不等式的性质,由 能推出 ,故本选项是正确的,因
此本题选D.
4.不等式x(x+2)<3的解集是( ).
A.{x|-13} D.¿,或x>1}
【答案】B
【解析】由题意x(x+2)<3,∴x2+2x-3<0即(x+3)(x-1)<0,解得:-3b>0)
A.当 时, 的最小值为 B.当 时, a2 b2
x2 y2
C: + =1(a>b>0)
C.当 无最大值 D.当 且 时, a2 b2
【答案】B
【解析】对于A,x+ 在[2,+∞)上单调增,所以x=2时, 的最小值为 ,故A错误;
对于B,当x>0时, ,当且仅当x=1时,等号成立,故B成立;对于C, 在(0,2]上单调增,所以x=2时, 取得最大值,故C不成立;
对于D,当0<x<1时,lgx<0, <0,结论不成立;
故选B
7.已知实数 ,则( )
A. B.
C. D.
【答案】C
【解析】 , , , ,
由于 ,在不等式上同时乘以 得 ,因此, ,故选:A.
8.已知 ,则 的最小值为
A.3 B.4 C.5 D.6
【答案】C
【解析】由题意,因为 ,则 ,
所以 ,
当且仅当 时,即 时取等号,
所以 的最小值为5,故选C.
9.某市原来居民用电价为0.52元 ,换装分时电表后,峰时段(早上八点到晚上九点)的电价0.55元,谷时段(晚上九点到次日早上八点)的电价为0.35元 .对于一个平均每月用电量为
的家庭,换装分时电表后,每月节省的电费不少于原来电费的 ,则这个家庭每月在峰时段
的平均用电量至多为 ( )
A. B. C. D.
【答案】C
【解析】设每月峰时段的平均用电量为 ,则谷时段的用电量为 ;
根据题意,得: ,
解得 .
所以这个家庭每月峰时段的平均用电量至多为 ,
故选C.
10.已知正数 满足
x+y=1
,则 的最小值为( )
14
A.5 B. 3 C. D.2
【答案】C
【解析∵正数 满足 ,∴ ,
∴
当且仅当 即 , 时,等号成立,即 的最小值为 ,故选C.
11.已知命题 ,命题 , ,则 成立是 成立的( )
A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件
【答案】A
【解析】求解不等式 可得 ,
对于命题 ,当 时,命题明显成立;
当 时,有: ,解得: ,
即命题 为真时 ,
故 成立是 成立的充分不必要条件.
故选:A.
12.已知二次函数 的二次项系数为 ,且不等式 的解集为 ,若方程
,有两个相等的根,则实数 ( )
A.- B. C. 或- D. 或-
【答案】A
【解析】由于不等式 的解集为 ,
即关于 的二次不等式 的解集为 ,则 .
由题意可知, 、 为关于 的二次方程 的两根,
由韦达定理得 , , , ,
,
由题意知,关于 的二次方程 有两相等的根,即关于 的二次方程 有两相等的根,
则 , ,解得 ,故选:A.
二、填空题(总分16分,每题4分)
13.已知a、b是正实数,且满足ab=a+b+3,则a+b的取值范围是________.
【答案】a+b≥6
【解析】∵a、b是正实数且ab=a+b+3,故a、b可视为一元二次方程x2-mx+m+3=0的两个根,其
中a+b=m,ab=m+3,要使方程有两个正根,应有
,得m≥6,
即a+b≥6,故a+b的取值范围是a+b≥6.
14.已知实数 、 ,满足 ,则 的取值范围是_____________.
【答案】-2