1996年黑龙江高考文科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_黑龙江

1996 年黑龙江高考文科数学真题及答案 第Ⅰ卷（选择题共65分） 注意事项： 1．答案Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡 上． 2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡 皮擦干净后，在选涂其它答案，不能答在试题卷上． 3．考试结束，监考人将本试卷和答题卡一并收回． 一．选择题：本大题共15小题；第1—10题每小题4分，第11—15题每小题5分，共65 分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1．设全集I 1,2,3,4,5,6,7，集合A1,3,5,7,B3,5．则 A．I  A B B．I  A B C．I  A B D．I  A B     【答案】C 【解析】显然C正确． 2．当a 1时，在同一坐标系中，函数y ax与y log x的图像 a 【答案】A 【解析】当a 1时，函数 y ax是减函数，且过点(0,1)；而函数 y log x为增函数， a 且过点(1,0)． 3．若sin2 xcos2 x，则x的取值范围是 第1页 | 共13页 3 1  A．x2k  x  2k ,kZ  4 4   1 5  B．x2k  x  2k ,kZ  4 4   1 1  C．xk  x  k ,kZ  4 4   1 3  D．xk  x  k ,kZ  4 4  【答案】D 1 2 2  【解析】sin2 xcos2 xsin2 x sinx 或sinx ，解得2k  x 2 2 2 4 3 3   2k (kZ)或2k  x2k (kZ)，即(2k1)  x(2k1) 4 4 4 4 3  1 3   (kZ)，所以x的取值范围是xk  x  k ,kZ． 4  4 4  (22i)4 4．复数 等于 (1 3i)5 A．1 3i B．1 3i C．1 3i D．1 3i 【答案】B (22i)4 24(1i)4 (2i)2 【解析】   1 3i． (1 3i)5 1 3 2()5 25(  i)5 2 2 5．6名同学排成一排，其中甲、乙两人必须排在一起的不同排法有 A．720种 B．360种 C．240种 D．120种 【答案】C 【解析】将甲、乙两人捆绑在一起，不同的排法有A5A2 240． 5 2 24  6．已知是第三象限角且sin ，则tan  25 2 第2页 | 共13页4 3 3 4 A． B． C． D． 3 4 4 3 【答案】D   sin 2sin2 7  1cos 2 2 【解析】由已知得cos ，所以tan    25 2    sin cos 2sin cos 2 2 2 7 1( ) 25 4   ． 24 3  25 7．如果直线l,m与平面,,满足：l  ,l//,m和m，那么必  有 A．且l m B．且m// C．m//且l m D．//且 【答案】A 【解析】略．   8．当  x 时，函数 f(x)sinx 3cosx的 2 2 1 A．最大值是1，最小值是1 B．最大值是1，最小值是 2 C．最大值是2，最小值是2 D．最大值是2，最小值是1 【答案】D    5 【解析】因为 f(x)sinx 3cosx2sin(x )，由已知  x  ．故当 3 6 3 6       x  ，即x 时， f(x)有最大值是2；当x  ，即x 时， f(x)有 3 2 6 3 6 2 最小值是1． 1 9．中心在原点，准线方程为x4，离心率为 的椭圆方程是 2 x2 y2 x2 y2 A ．  1 B ．  1 4 3 3 4 第3页 | 共13页x2 y2 C．  y2 1 D．x2  1 4 4 【答案】A a2 c 1 x2 y2 【解析】由题设可得 4,  ，解得a2,c1，所以椭圆方程是  1． c a 2 4 3 10．圆锥母线长为1，侧面展开图圆心角为240，该圆锥的体积是 2 2 8 4 5 10 A． B． C． D． 81 81 81 81 【答案】C 2r 240 2 【解析】设圆锥底面半径为 r，则  2，得 r  ，则圆锥高为 1 360 3 2 5 1( )2  ， 3 3 1 2 5 4 5 圆锥的体积是 ( )2  ． 3 3 3 81 11．椭圆25x2 150x9y2 18y90的两个焦点坐标是 A．(3,5),(3,3) B．(3,3),(3,5) C．(1,1),(7,1) D．(7,1),(1,1) 【答案】B (y1)2 (x3)2 y2 x2 【解析】椭圆的标准方程为  1，而  1的焦点为(0,4)，所以 52 32 52 32 (y1)2 (x3)2  1的焦点坐标是(3,3),(3,5)． 52 32 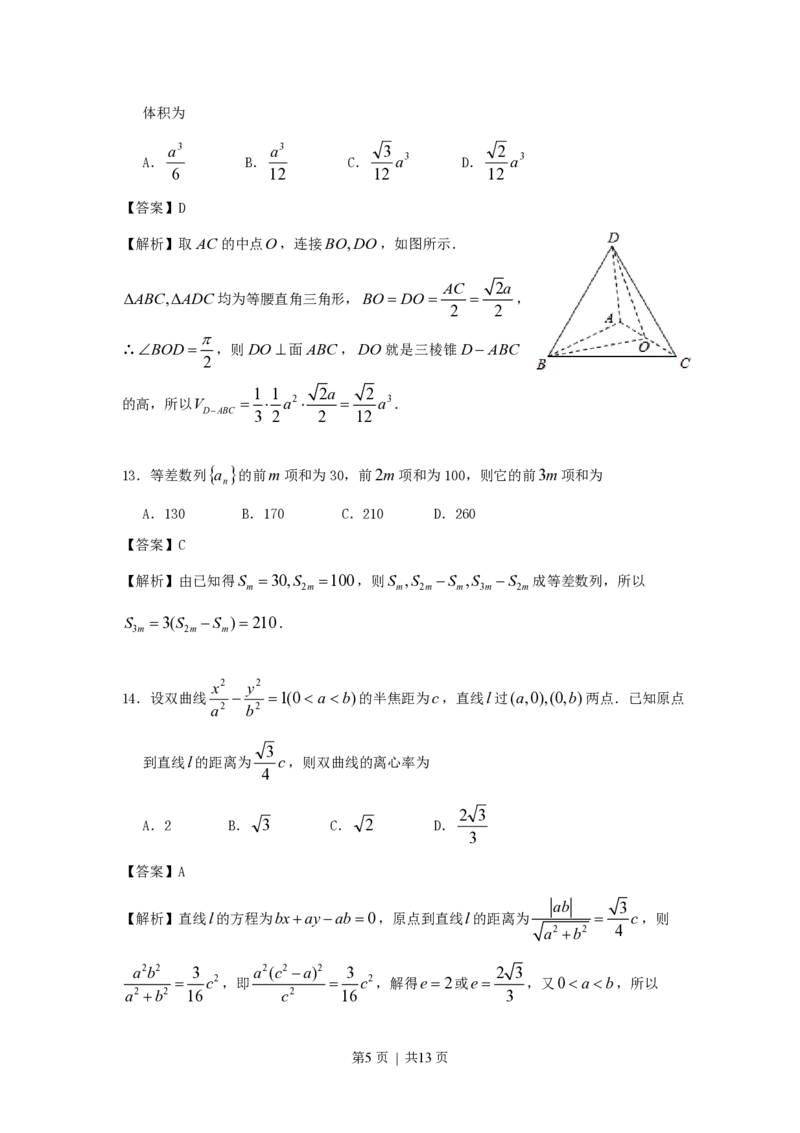12．将边长为a的正方形ABCD沿对角线AC折起，使得BDa，则三棱锥DABC的 第4页 | 共13页体积为 a3 a3 3 2 A． B． C． a3 D． a3 6 12 12 12 【答案】D 【解析】取AC的中点O，连接BO,DO，如图所示． AC 2a ABC,ADC均为等腰直角三角形，BO DO  ， 2 2  ∴BOD ，则DO面 ABC，DO就是三棱锥DABC 2 1 1 2a 2 的高，所以V   a2  a3． DABC 3 2 2 12   13．等差数列 a 的前m项和为30，前2m项和为100，则它的前3m项和为 n A．130 B．170 C．210 D．260 【答案】C 【解析】由已知得S 30,S 100，则S ,S S ,S S 成等差数列，所以 m 2m m 2m m 3m 2m S 3(S S )210． 3m 2m m x2 y2 14．设双曲线  1(0 a b)的半焦距为c，直线l过(a,0),(0,b)两点．已知原点 a2 b2 3 到直线l的距离为 c，则双曲线的离心率为 4 2 3 A．2 B． 3 C． 2 D． 3 【答案】A ab 3 【解析】直线l的方程为bxayab0，原点到直线l的距离为  c，则 a2 b2 4 a2b2 3 a2(c2 a)2 3 2 3  c2，即  c2，解得e2或e ，又0ab，所以 a2 b2 16 c2 16 3 第5页 | 共13页a2 b2 b2 2 3 e  1  2，所以e 不合题意． a2 a2 3 15． f(x)是(,)上的奇函数， f(x2)f(x)，当0 x1时， f(x) x，则 f(7.5) 等于 A．0.5 B．0.5 C．1.5 D．1.5 【答案】B 【解析】 f(7.5) f(5.52)f(5.5)[f(3.5)] f(3.5)f(1.5)[f(0.5)] f(0.5)0.5． 第Ⅱ卷（非选择题共85分） 注意事项： 1．第Ⅱ卷共6页，用钢笔或圆珠笔直接答在试题卷中． 2．答卷前将密封线内的项目填写清楚． 二．填空题：本大题共4小题；每小题4分，共16分．把答案填在题中横线上． 16．已知点(2,3)与抛物线y2  2px(p 0)的焦点的距离是5，则 p  ． 【答案】4 p 【解析】由已知得 ( 2)2 32 5，解得 p4． 2 17．正六边形的中心和顶点共7个点，以其中3个点为顶点的三角形共有 个．（用 数字作答） 【答案】32 【解析】从7个点中取3个点有C3种取法，3个点共线的有3种，三角形共有C3 332 7 7 个． 第6页 | 共13页18．tg20 tg40  3tg20tg40的值是 ． 【答案】 3 tg20 tg40 【解析】∵tg(20 40)  3，∴tg20 tg40  3(1-tg20tg40)， 1tg20tg40 tg20 tg40  3tg20tg40  3． 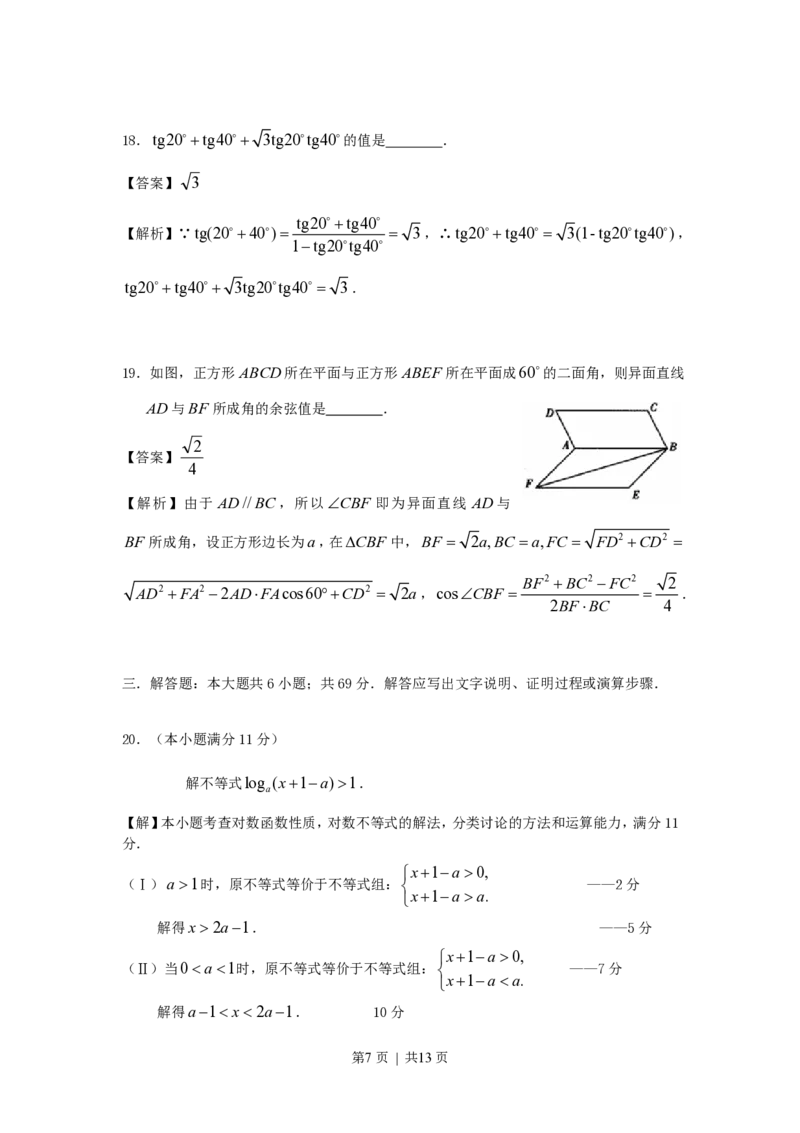19．如图，正方形ABCD所在平面与正方形ABEF所在平面成60的二面角，则异面直线 AD与BF 所成角的余弦值是 ． 2 【答案】 4 【解析】由于 AD//BC，所以CBF 即为异面直线 AD与 BF 所成角，设正方形边长为a，在CBF 中，BF  2a,BC a,FC  FD2 CD2  BF2 BC2 FC2 2 AD2 FA2 2ADFAcos60CD2  2a，cosCBF   ． 2BFBC 4 三．解答题：本大题共6小题；共69分．解答应写出文字说明、证明过程或演算步骤． 20．（本小题满分11分） 解不等式log (x1a)1． a 【解】本小题考查对数函数性质，对数不等式的解法，分类讨论的方法和运算能力，满分11 分． x1a0, （Ⅰ）a 1时，原不等式等价于不等式组： ——2分 x1aa. 解得x2a1． ——5分 x1a0, （Ⅱ）当0a1时，原不等式等价于不等式组： ——7分 x1aa. 解得a1 x2a1． 10分 第7页 | 共13页  综上，当a 1时，不等式的解集为 x x2a1 ；   当0a1时，不等式的解集为 x a1 x2a1 ． ——11分 21．（本小题满分12分） 设等比数列a 的前n项和为S ．若S S 2S ，求数列的公比q． n n 3 6 9 【解】本小题主要考查等比数列的基础知识，逻辑推理能力和运算能力．满分12分． 若q 1，则有S 3a ,S 6a ,S 9a ．但a 0， 3 1 6 1 9 1 1 即得S S 2S ，与题设矛盾，故q 1． ——2分 3 6 9 a (1q3) a (1q6) 2a (1q9) 又依题意S S 2S 可得 1  1  1 ． 3 6 9 1q 1q 1q 整理得q3(2q6 q3 1)0． 由q 0得方程2q6 q310．(2q3 1)(q3 1)0， —— 9分 3 4 ∵ q1,q3 1，∴2q310，∴q  ． ——12分 2 22．（本小题满分11分） 1 1 2 已知ABC的三个内角A,B,C满足：AC  2B,    ，求 cosA cosC cosB AC cos 的值． 2 解法一：由题设条件知B60,AC 120． ——2分  2 1 1 ∵ 2 2 ，∴   2 2． cos60 cosA cosC 将上式化为cosAcosC  2 2cosAcosC ． 利用和差化积及积化和差公式，上式可化为 AC AC 2cos cos   2[cos(AC)cos(AC)]． ——6分 2 2 第8页 | 共13页AC 1 1 将cos cos60  ,cos(AC)   代入上式得 2 2 2 AC 2 cos   2cos(AC)． 2 2 AC 将cos(AC)  2cos2( )1代入上式并整理得 2 AC AC 4 2cos2( )2cos( )3 2 0 ——9分 2 2 AC AC (2cos  2)(2 2cos 3)0， 2 2 AC AC ∵2 2cos 30，∴2cos  2 0． 2 2 AC 2 从而得cos  ． ——12分 2 2 解法二：由题设条件知B60,AC 120． AC 设 ，则AC 2，可得A60 ,C 60 ， ——3分 2 1 1 1 1 所以    cosA cosC cos(60 ) cos(60 ) 1 1   1 3 1 3 cos sin cos sin 2 2 2 2 cos cos   ． ——7分 1 3 3 cos2 sin2 cos2 4 4 4 cos  2 依题设条件有  ， 3 cosB cos2 4 1 cos ∵cosB  ，∴  2 2 ． 2 3 cos2 4 整理得4 2cos22cos3 2 0, ——9分 (2cos 2)(2 2cos3)0， ∵2 2cos3 0，∴2cos 2 0． 第9页 | 共13页AC 2 从而得cos  ． ——11分 2 2 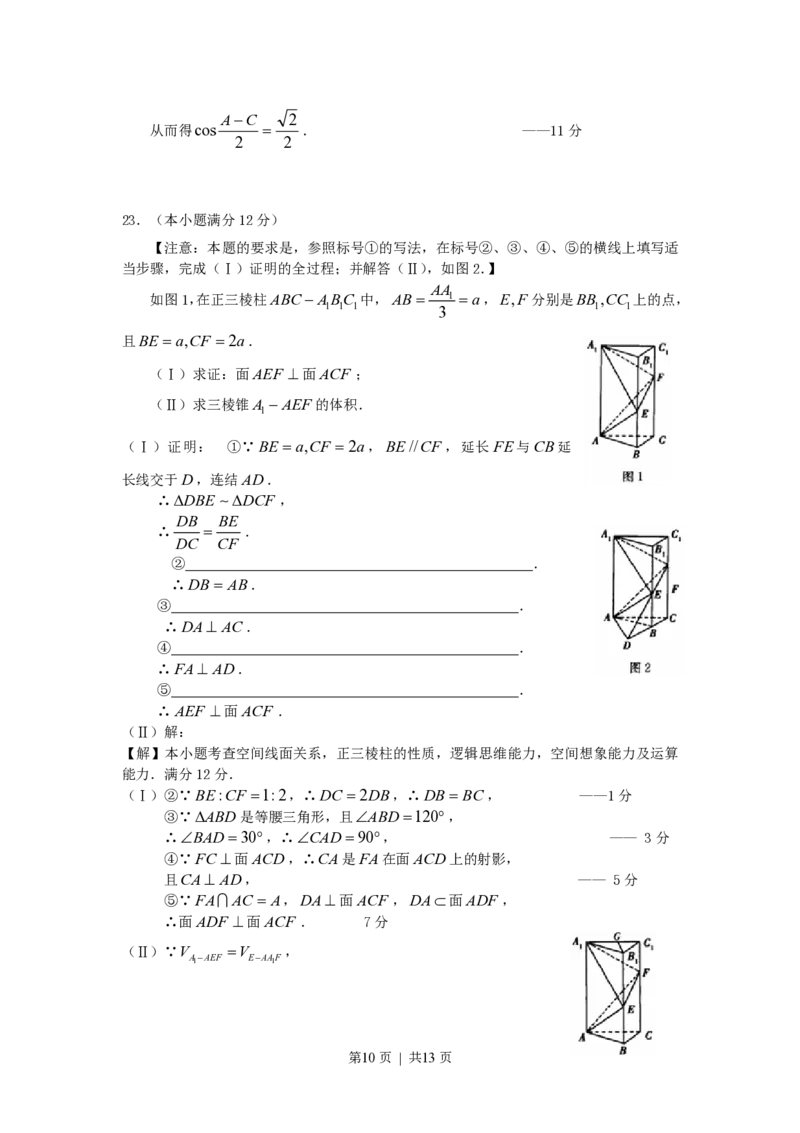23．（本小题满分12分） 【注意：本题的要求是，参照标号①的写法，在标号②、③、④、⑤的横线上填写适 当步骤，完成（Ⅰ）证明的全过程；并解答（Ⅱ），如图2．】 AA 如图1，在正三棱柱ABCABC 中，AB 1 a，E,F分别是BB,CC 上的点， 1 1 1 3 1 1 且BE a,CF 2a． （Ⅰ）求证：面AEF 面ACF ； （Ⅱ）求三棱锥A AEF的体积． 1 （Ⅰ）证明： ①∵BE a,CF 2a，BE//CF，延长FE与CB延 长线交于D，连结AD． ∴DBE DCF ，  DB BE ∴  ． DC CF ② ． ∴DB AB． ③ ． ∴DA AC． ④ ． ∴FA AD． ⑤ ． ∴AEF 面ACF ． （Ⅱ）解： 【解】本小题考查空间线面关系，正三棱柱的性质，逻辑思维能力，空间想象能力及运算 能力．满分12分． （Ⅰ）②∵BE:CF 1:2，∴DC 2DB，∴DB BC， ——1分 ③∵ABD是等腰三角形，且ABD120， ∴BAD30，∴CAD90， —— 3分 ④∵FC 面ACD，∴CA是FA在面ACD上的射影， 且CA AD， —— 5分 ⑤∵FA AC  A，DA面ACF ，DA面ADF，  ∴面ADF 面ACF ． 7分 （Ⅱ）∵V V ， AAEF EAAF 1 1 第10页 | 共13页3a 在面ABC 内作BG  AC ，垂足为G．BG  ． 1 1 1 1 1 1 1 2 面ABC 面AC，∴BG 面AC， 1 1 1 1 1 1 3a ∵EBB ，而BB //面AC，∴三棱柱EAAF 的高为 ．——9分 1 1 1 1 2 1 3a2 S  AA AC  ． ——10分 A 1 FA 2 1 2 3a3 ∴V V  ． ——12分 A 1 AEF EAA 1 F 4 24．（本小题满分10分） 某地现有耕地10000公顷，规划10年后粮食单产比现在增加22%，人均粮食占有量比 现在提高10%．如果人口年增长率为1%，那么耕地平均每年至多只能减少多少公顷（精确到 总产量 总产量 1公顷）?（粮食单产= ，人均粮食占有量= ） 耕地面积 总人口数 【解】本小题主要考查运用数学知识和方法解决实际问题的能力，指数函数和二项式定理的 应用，近似计算的方法和能力．满分10分． 设耕地平均每年至多只能减少x公顷，又设该地区现有人口为P人，粮食单产为M 吨/ 公顷． M (122%)(104 10x) M 104 依题意得不等式  (110%)．——5分 P(11%)10 P 1.1(10.01)10 化简得x 103 [1 ]． ——7分 1.22 1.1(10.01)10 1.1 ∵103[1 ]103[1 (1C1 0.01C2 0.012  )] 1.22 1.22 10 10  1.1 103[1 1.1045]4.1． —— 9分 1.22 ∴x4（公顷）． 答：按规划该地区耕地平均每年至多只能减少4公顷． ——10分 第11页 | 共13页25．（本小题满分12分） 已知l ,l 是过点P( 2,0)的两条互相垂直的直线，且l ,l 与双曲线y2 x2 1各有两 1 2 1 2 个交点，分别为A,B 和A ,B ． 1 1 2 2 （Ⅰ）求l 的斜率k 的取值范围； 1 1 （Ⅱ）若A恰是双曲线的一个顶点，求 A B 的值． 1 2 2 【解】本小题主要考查直线与双曲线的性质，解析几何的基本思想，以及综合运用知识的 能力．满分12分． （Ⅰ）依题设，l ,l 的斜率都存在，因为l 过点P( 2,0)且与双曲线有两个交点，故方程 1 2 1  y k (x 2)(k 0), 组 1 1 ① ——1分 y2 x2 1. 有两个不同的解． 在方程组①中消去y，整理得(k2 1)x2 2 2k2x2k2 10． ② 1 1 1 若k2 10，则方程组①只有一个解，即l 与双曲线只有一个交点，与题设矛盾，故 1 1 k2 1 0，即 k 1，方程②的判别式为 1 1  (2 2k2)2 4(k2 1)(2k2 1)4(3k2 1)． 1 1 1 1 1 设l 的斜率为k ，因为l 过点P( 2,0)且与双曲线有两个交点，故方程组 2 2 2  y  k (x 2)(k  0),  2 2 ③  y2 x2 1. 有两个不同的解．在方程组③中消去y，整理得 (k2 1)x2 2 2k2x2k2 10． ④ 2 2 2 同理有k2 1 0,  4(3k2 1)． 2 2 2 又因为l l ，所以有l l 1． ——4分 1 2 1 2 第12页 | 共13页3k2 10, 1  3k2 10, 于是，l ,l 与双曲线各有两个交点，等价于 2 1 2 k k  1,  1 2  k 1.  1  3   k  3, 解得 3 1 ——6分  k 1.  1 3 3 ∴k ( 3,1) (1, ) ( ,1) (1, 3)． ——7分 1  3  3  （Ⅱ）双曲线y2 x2 1的顶点为(0,1),(0,1)． 取A(0,1)时，有k (0 2)1， 1 1 2 1 解得k  ．从而k   2． ——8分 1 2 2 k 1 将k  2代入方程④得x2 4 2x30． ⑤ 2 记l 与双曲线的两交点为A (x ,y ),B (x ,y )，则 2 2 1 1 2 2 2 A B 2 (x x )2 (y y )2 3(x x )2 3[(x x )2 4x x ]． 2 2 1 2 2 1 2 1 2 1 2 由⑤知x x )4 2,x x 3． 1 2 1 2 2 ∴ A B 60, A B 2 15． ——11分 2 2 2 2 当取A(0,1)时，由双曲线y2 x2 1关于x轴的对称性，知 A B 2 15． 1 2 2 所以l 过双曲线的一个顶点时， A B 2 15． ——12分 1 2 2 第13页 | 共13页