文档内容
第四章 指数函数与对数函数
复习与小结
一、选择题
1.(2019·广东佛山一中高一期中)函数 的定义域为( )
A. B. C. D.
【答案】C
【解析】:要使函数有意义 需满足: ,
得 ,且 ,故函数的定义域为 .故选:C
2.(2019·贵州高一期中)计算: ( )
A. B. C. D.
【答案】C
【解析】原式 .故选:C
3.(2019·广西高一期中)以下函数在 上是减函数的是( )
A. B. C. D.
【答案】D
【解析】选项A:在 上先增后减;
选项B:定义域为:(0,+∞),在(0,+∞)上是减函数,不满足在 上是减函数;
选项C:定义域中就没有0,不满足在 上是减函数;选项D正确.故选:D.
4.(2019·吉林高一期中) 的零点所在区间为( )A. B. C. D.
【答案】C
【解析】 , ,
,
,根据零点存在性定理可得 ,则
的零点所在区间为 故选:C
5.(2019·江西宜春九中高一期中)若 则,它们的大小关系正确的
是( )
A. B. C. D.
【答案】A
【解析】∵y 为减函数,y 为减函数,
∴a 1,c 0,
又y=log x为增函数,∴0=log 1<b=log 2<log 3=1,∴a>b>c.故选:A.
3 3 3 3
6.(2019·山东高一期中)若 ,则 的取值范围是( )
A. B. C. D.
【答案】C
【解析】当 时, ,成立,当 时, , ,
综上 .故选:C.7.(2019·河北邯郸一中高一期中)已知函数 是奇函数,且当 时, ,则
的值为( )
A. B. C. D.
【答案】B
【解析】 ;
又x<0时,f(x)=5﹣x﹣1,且f(x)为奇函数;
∴ 2.故选:B.
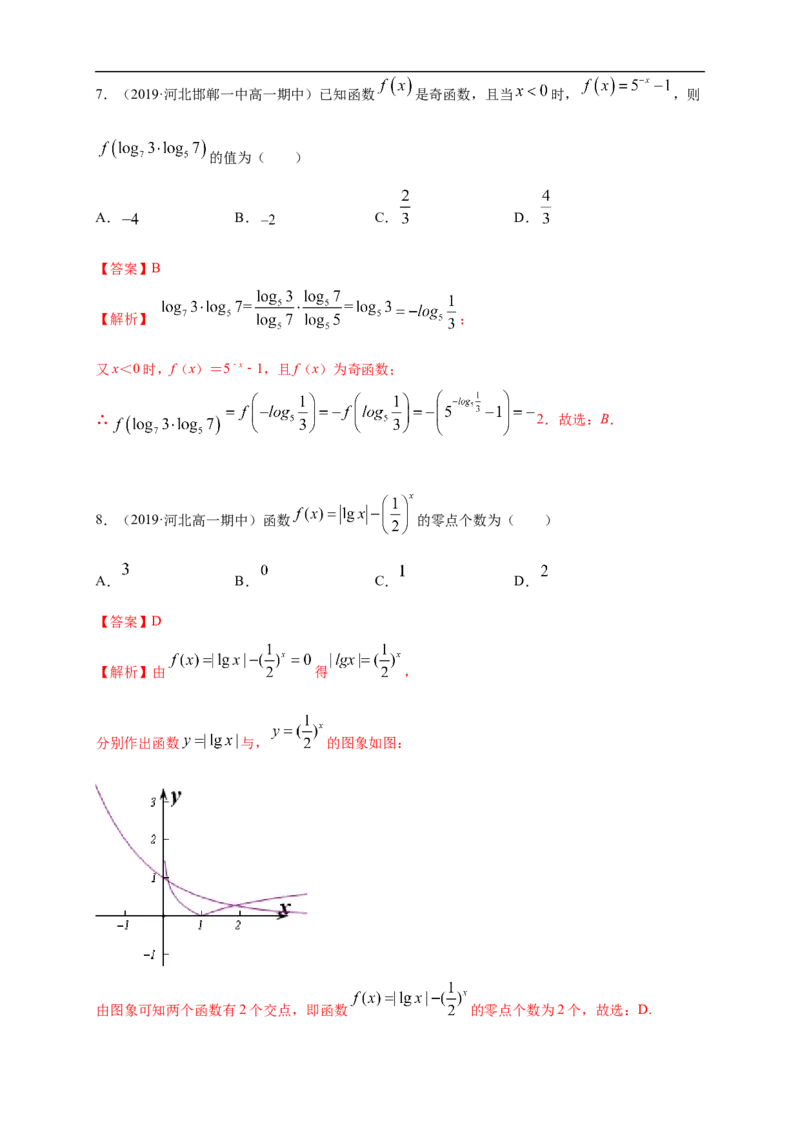
8.(2019·河北高一期中)函数 的零点个数为( )
A. B. C. D.
【答案】D
【解析】由 得 ,
分别作出函数 与, 的图象如图:
由图象可知两个函数有2个交点,即函数 的零点个数为2个,故选:D.9.(2019·江苏高一期中)数学学习的最终目标:让学习者会用数学眼光观察世界,会用数学思维
思考世界,会用数学语言表达世界.“双11”就要到了,电商的优惠活动很多,某同学借助于已学数
学知识对“双11”相关优惠活动进行研究.已知2019年“双11”期间某商品原价为 元,商家准备在
节前连续2次对该商品进行提价且每次提价 ,然后在“双11”活动期间连续2次对该商品进行
降价且每次降价 .该同学得到结论:最后该商品的价格与原来价格 元相比( ).
A.相等 B.略有提高 C.略有降低 D.无法确定
【答案】C
【解析】设现价为 ,则 ,则 ,则该商品的价格与原来
价格相比略有降低,故选:C.
10.(2019·福建厦门外国语学校高一期中)一元二次方程 的两根均大于 ,则实
数 的取值范围是( )
A. B. C. D.
【答案】C
【解析】设 ,则二次函数 的图象开口向上,
对称轴为直线 .由于一元二次方程 的两根均大于 ,
则 ,解得 ,因此,实数 的取值范围是 .
二、填空题
11.(2019·陕西高一期中)已知函数 ,若 ,则
【答案】3
【解析】 ;.故f(x)+ ,则
12.(2017·北京清华附中高一期中)已知函数 ,给出下列命题:
①若 ,则 ;
②对于任意的 , , ,则必有 ;
③若 ,则 ;
④若对于任意的 , , ,则 ,其中所有正确命题
的序号是_____.
【答案】②④
【解析】 ,
对于①,当 时, ,故①错误.
对于②, 在 上单调递减,所以当 时 ,
即: ,故②正确.
对于③ 表示图像上的点与原点连线的斜率,由 的图像可知,
当 时, ,即: ,故③错误.
对于④,由 得图像可知, ,故④正确.
综上所述,正确命题的序号是②④.13.(2017·天津高一期中)若关于 的不等式 在 内恒成立,则 的取值范
围是__________.
【答案】
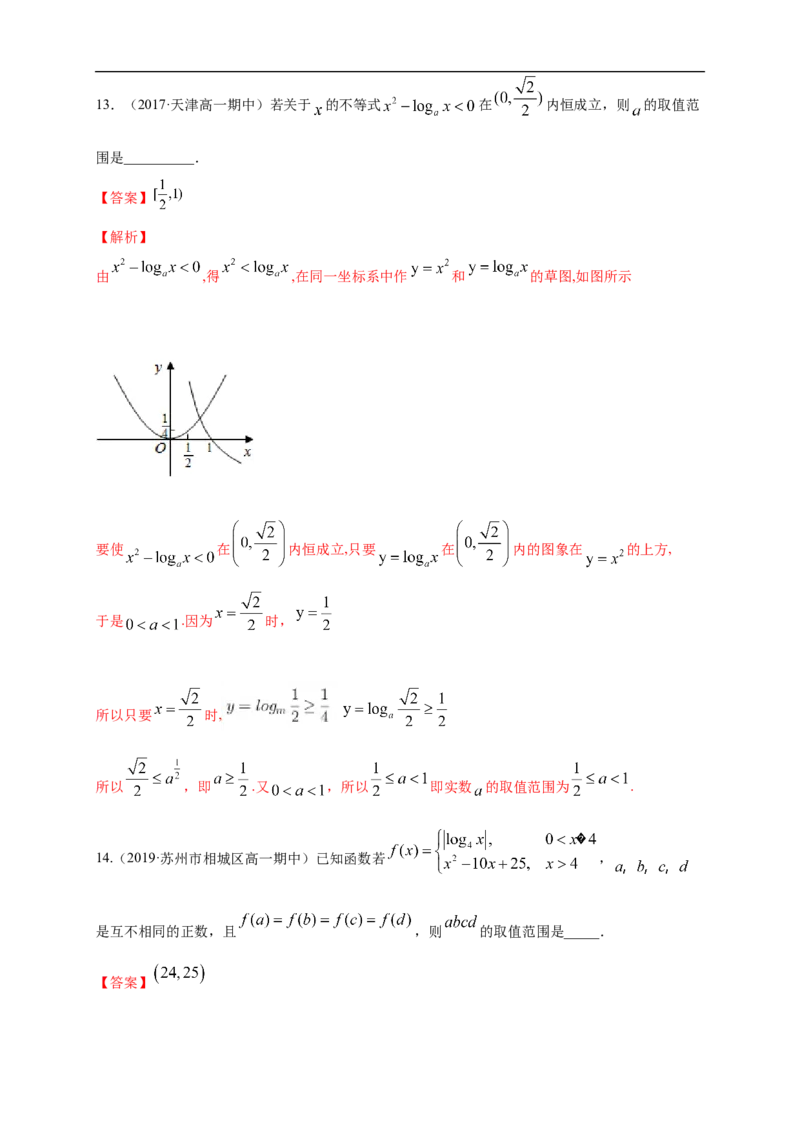
【解析】
由 ,得 ,在同一坐标系中作 和 的草图,如图所示
要使 在 内恒成立,只要 在 内的图象在 的上方,
于是 .因为 时,
所以只要 时,
所以 ,即 .又 ,所以 即实数 的取值范围为 .
14.(2019·苏州市相城区高一期中)已知函数若 ,
是互不相同的正数,且 ,则 的取值范围是_____.
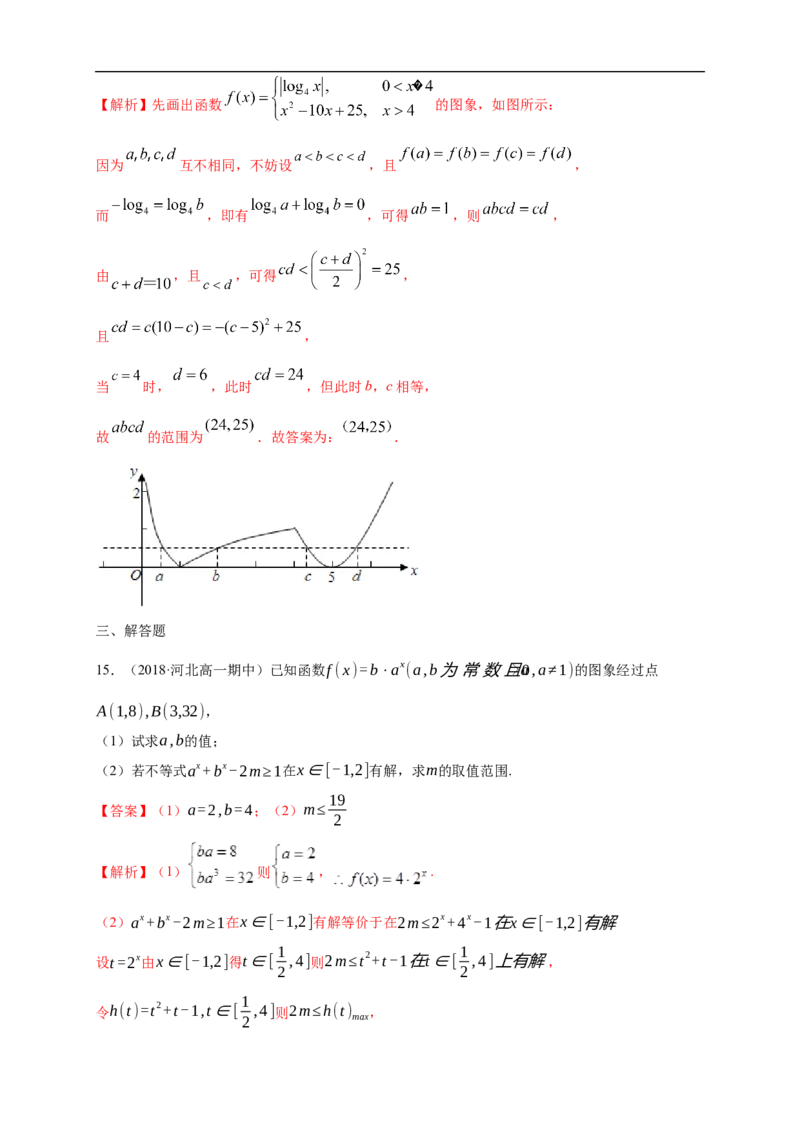
【答案】【解析】先画出函数 的图象,如图所示:
因为 互不相同,不妨设 ,且 ,
而 ,即有 ,可得 ,则 ,
由 ,且 ,可得 ,
且 ,
当 时, ,此时 ,但此时b,c相等,
故 的范围为 .故答案为: .
三、解答题
15.(2018·河北高一期中)已知函数f(x)=b⋅ax (a,b为常数且>a0,a≠1)的图象经过点
A(1,8),B(3,32),
(1)试求a,b的值;
(2)若不等式ax+bx-2m≥1在x∈[-1,2]有解,求m的取值范围.
19
【答案】(1)a=2,b=4;(2)m≤
2
【解析】(1) 则 , .
(2)ax+bx-2m≥1在x∈[-1,2]有解等价于在2m≤2x+4x-1在x∈[-1,2]有解
1 1
设t=2x由x∈[-1,2]得t∈[ ,4]则2m≤t2+t-1在t∈[ ,4]上有解,
2 2
1
令h(t)=t2+t-1,t∈[ ,4]则2m≤h(t) ,
2 max1 2 5 1
又h(t)=t2+t-1=(t+ ) - 在[ ,4]上为增函数,
2 4 2
19
所以h(t) =h(4)=19所以2m≤19,所 以m≤ .
max 2
16.(2019·湖北高一期中)已知A, B两地的距离是130 km,每辆汽车的通行费为50元.按交通法规
规定, A, B两地之间的公路车速应限制在50~100 km/h.假设汽油的价格是7元/L , 一辆汽车的耗油
率
(L/h)与车速的平方成正比,如果此车的速度是90 km/h,那么汽车的耗油率为22.5 L/h,司机每小时的工
资是70元.从A地到B地最经济的车速是多少?如果不考虑其它费用,这次行车的总费用是多少(精确
到1元)?
【答案】最经济的车速是60 km/h,此时的行车总费用约为 元.
【解析】设车速为 ,油耗率为 ,行车总费用为 ,
因为一辆汽车的耗油率(L/h)与车速的平方成正比,所以 ( ),
又此车的速度是90 km/h时,汽车的耗油率为22.5 L/h,
所以 ,解得 ,故 ,
因此,由题意可得,
,
当且仅当 ,即 时, 取最小值.
因此,从A地到B地最经济的车速是60 km/h,此时的行车总费用约为 元.
17.(2019·广东实验中学高一期中)已知定义域为 的函数 是奇函数
(1)求 的值
(2)判断并证明该函数在定义域 上的单调性
(3)若对任意的 ,不等式 恒成立,求实数 的取值范围。【答案】(1) (2)减函数,证明见解析(3)
【解析】(1)由题设,需 。经验证, 为奇函数,
(2)减函数.证明:任取 , ,
, ,所以 在 上是减函数.
(3)由 得 ,
是奇函数, ,由(2)知 在是减函数,
故原问题可化为 即: 对任意 恒成立,
,解得 .
18.(2019·江苏高一期中)已知函数 ,其中 ,记函数
的定义域为 .
(1)求函数 的定义域 ;
(2)若函数 的最大值为 ,求 的值;
(3)若对于 内的任意实数 ,不等式 恒成立,求实数 的取值范围.
【答案】(1) .(2) .(3) .
【解析】(1)要使函数有意义:则有 ,解得-2<x<1,∴ 函数的定义域 为
(2)因为 , 所以
因为 ,所以 ,
即 , 由 ,得 ,
(3)由 在 恒成立,
得 ,因为 ,所以
所以 在 恒成立
设 ,令 ,则
即 ,因为 ,
所以 (当且仅当 时,取等号
所以 ,所以