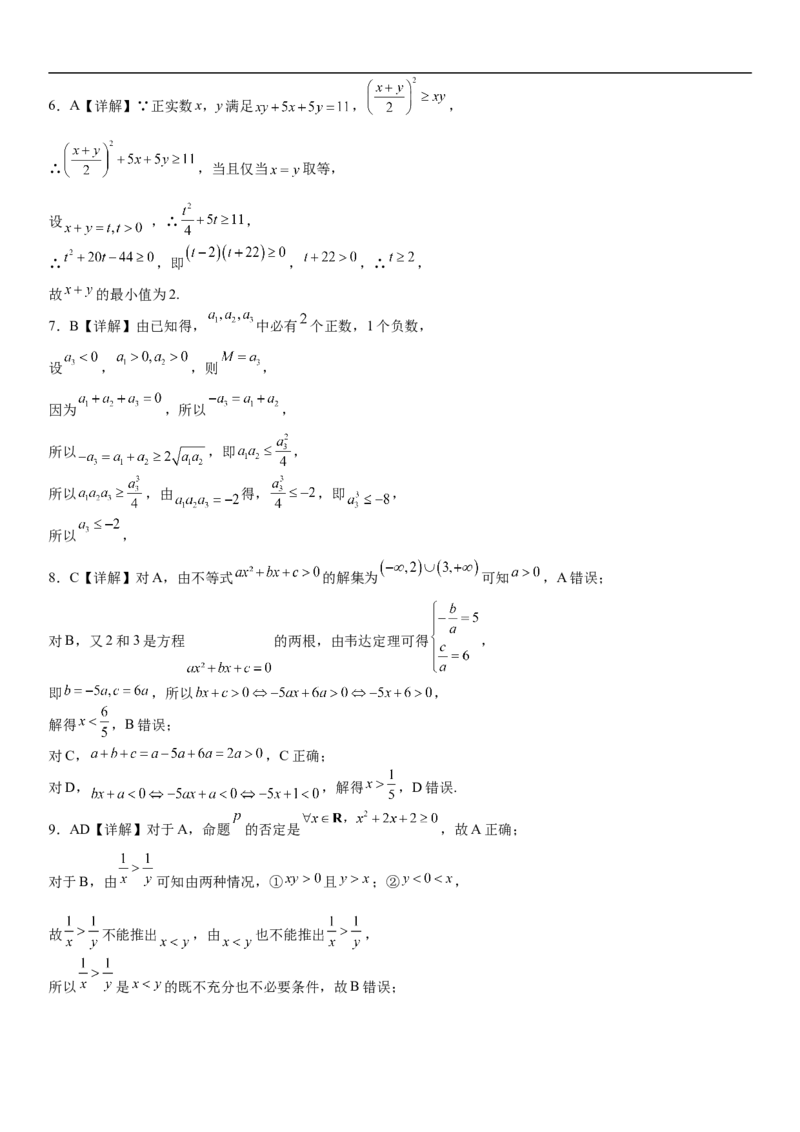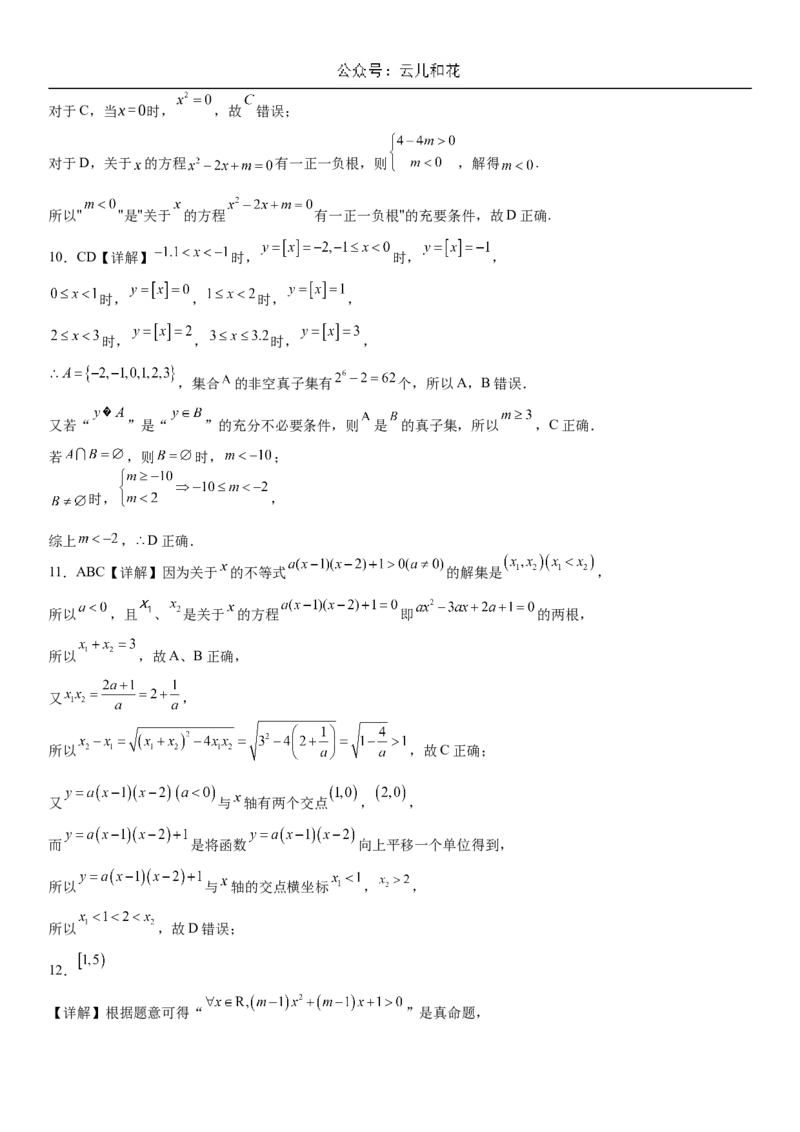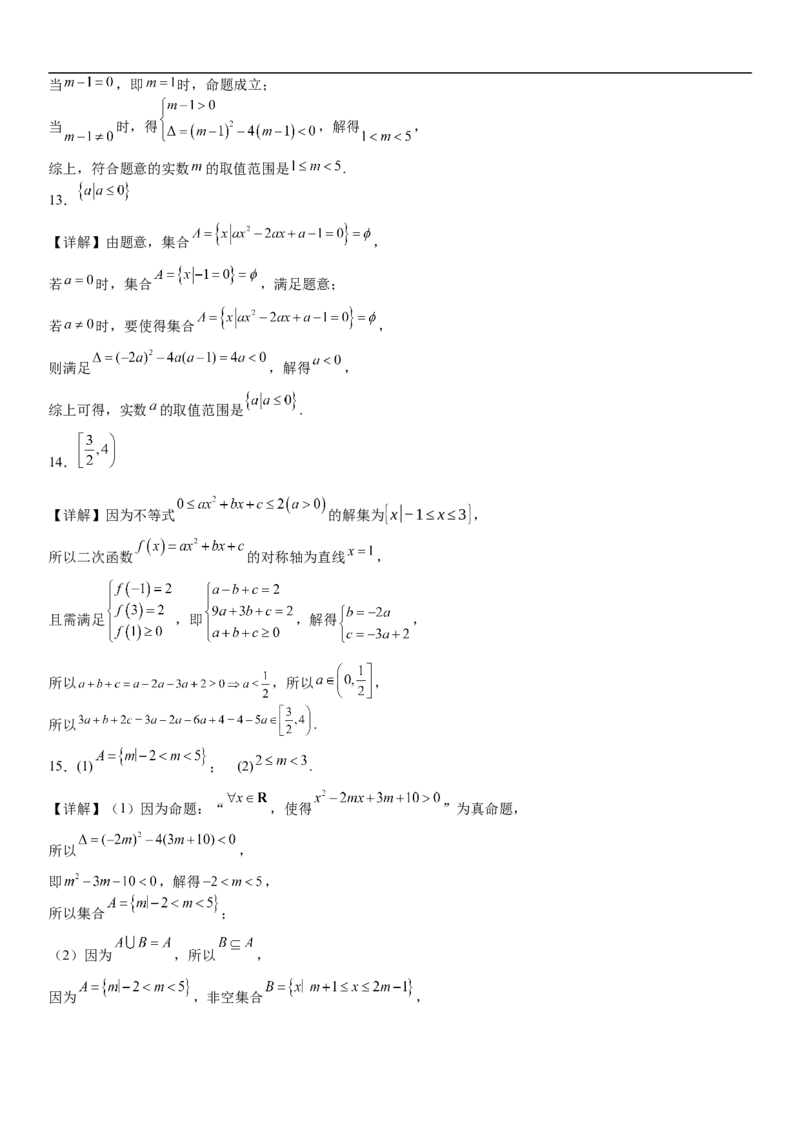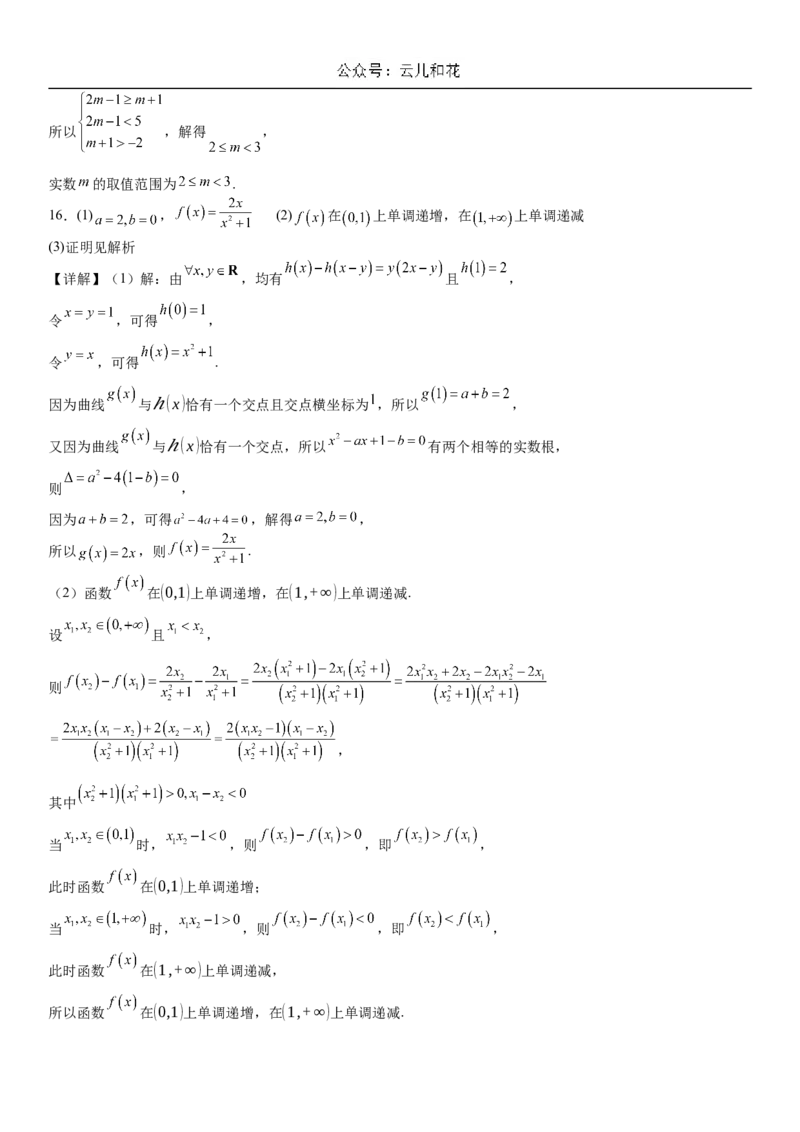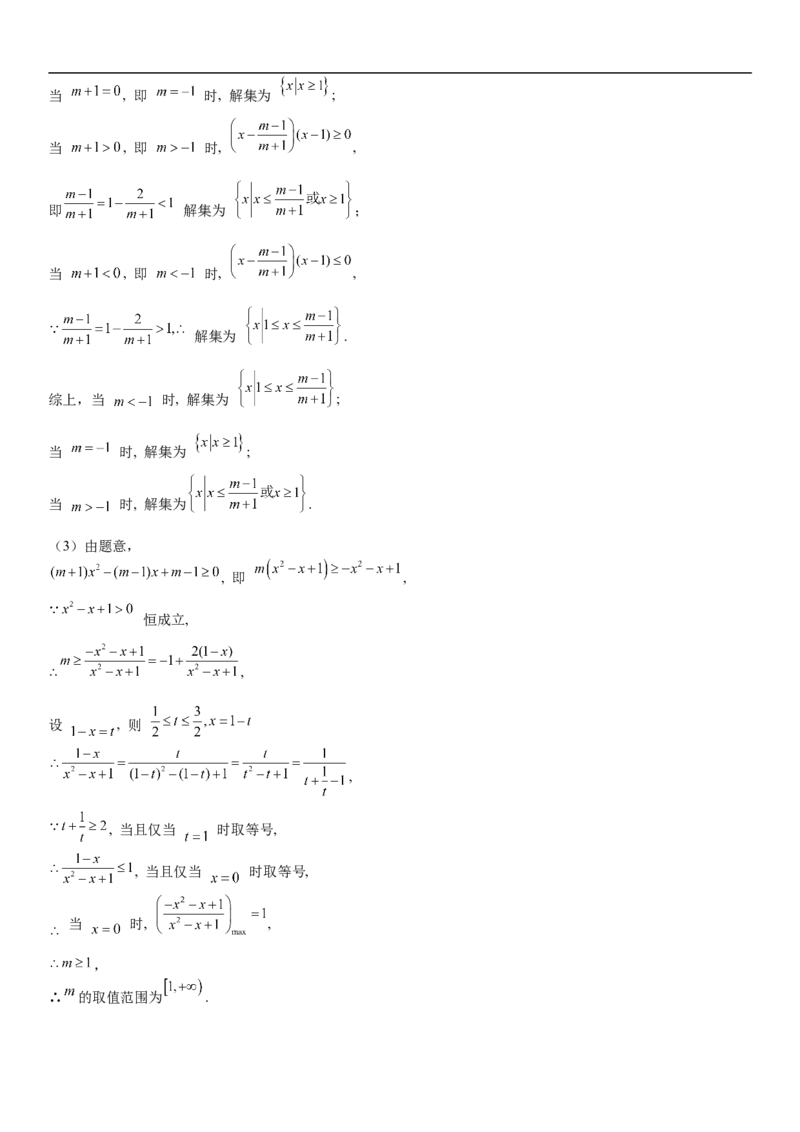文档内容
2024-2025 学年高一上学期 10 月检测
数 学
注意事项:
1.答卷前,考生务必将自己的姓名和座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡皮擦干净
后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡的相应位置上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一.选择题(共8小题,每小题5分,共40分,每小题给出的四个选项中,只有一项是符合题目要求的。)
1.已知函数 的定义域为 ,则函数 的定义域为( )
A. B. C. D.
2.设命题 ,则 为( )
A. B.
C. D.
3.下列各组函数是同一个函数的是( )
A. 与 B. 与
C. 与 D. 与
4.当一个非空数集 满足“如果 ,则 , , ,且 时, ”时,我们称 就是一个
数域,以下四个数域的命题:
①0是任何数域的元素:②若数域 有非零元素,则 ;
③集合 是一个数域
④有理数集是一个数域
其中真命题的个数为( )
A.1 B.2 C.3 D.4
5.定义运算: .若关于 的不等式 恒成立,则实数 的取值范围为( )
A. B.
C. D.
6.若正实数 , 满足 ,则 的最小值为( )
A.2 B.3 C.4 D.5
7.存在三个实数 ,使其分别满足下述两个等式:
(1) (2)
其中M表示三个实数 中的最小值,则( )
A.M的最大值是 B.M的最大值是
C.M的最小值是 D.M的最小值是
8.已知关于 的不等式 的解集为 ,则( )
A. B.不等式 的解集是C. D.不等式 的解集为 或
二.多选题(共3小题,每题6分,共18分。在每题给出的选项中,有多项符合题目要求。全部选对得6分,部
分选对得3分,有选错的得0分。)
9.下列说法中正确的有()
A.命题 , ”则命题 的否定是
B.“ ”是“ ”的必要不充分条件
C.命题“ ”是真命题
D.“ ”是“关于 的方程 有一正一负根”的充要条件
10.已知 表示不超过 的最大整数,例如: ,
,下列说法正确的是( )
A.集合
B.集合 的非空真子集的个数是30个
C.若“ ”是“ ”的充分不必要条件,则
D.若 ,则
11.已知关于 的不等式 的解集是 ,则( )
A. B. C. D.
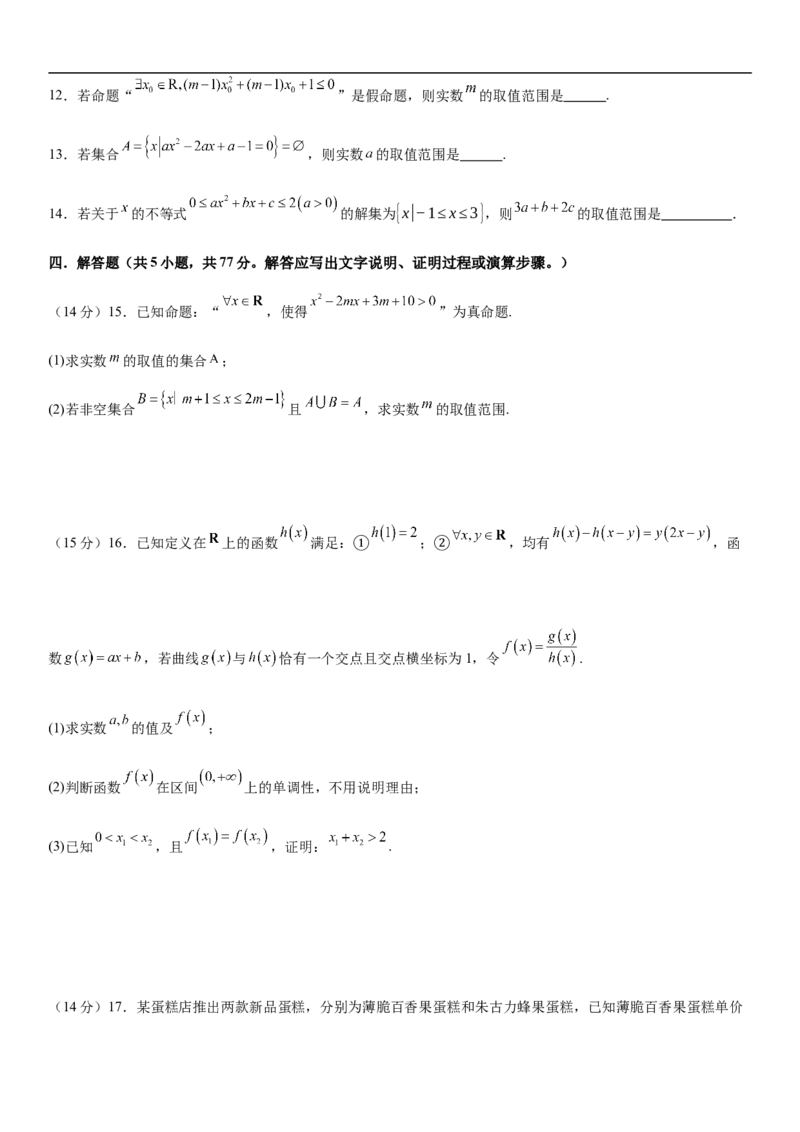
三.填空题(共3小题,每题5分,共15分。)12.若命题“ ”是假命题,则实数 的取值范围是 .
13.若集合 ,则实数 的取值范围是 .
14.若关于 的不等式 的解集为{x|−1≤x≤3},则 的取值范围是 .
四.解答题(共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。)
(14分)15.已知命题:“ ,使得 ”为真命题.
(1)求实数 的取值的集合 ;
(2)若非空集合 且 ,求实数 的取值范围.
(15分)16.已知定义在 上的函数 满足: ; ,均有 ,函
① ②
数 ,若曲线 与 恰有一个交点且交点横坐标为1,令 .
(1)求实数 的值及 ;
(2)判断函数 在区间 上的单调性,不用说明理由;
(3)已知 ,且 ,证明: .
(14分)17.某蛋糕店推出两款新品蛋糕,分别为薄脆百香果蛋糕和朱古力蜂果蛋糕,已知薄脆百香果蛋糕单价为x元,朱古力蜂果蛋糕单位为y元,现有两种购买方案:
方案一:薄脆百香果蛋糕购买数量为a个,朱古力蜂果蛋糕购买数量为b个,花费记为 ;
方案二:薄脆百香果蛋糕购买数量为b个,朱古力蜂果蛋糕购买数量为a个,花费记为 .
(其中 )
(1)试问哪种购买方案花费更少?请说明理由;
(2)若a,b,x,y同时满足关系 ,求这两种购买方案花费的差值S最小值(注:差值
花费较大值-花费较小值).
(16分)18.已知命题 , ,命题 , .
(1)当命题 为假命题时,求实数 的取值范围;
(2)若命题 和 中有且仅有一个是假命题,求实数 的取值范围.
(18分)19.已知函数 .
(1)若不等式 的解集为 ,求 的取值范围;
(2)解关于 的不等式 ;
(3)若不等式 对一切 恒成立,求 的取值范围.数学答案
1.B【详解】由题意得: ,解得: ,
由 ,解得: ,
故函数的定义域是 ,
2.B【详解】由全称命题的否定为特称命题,则原命题的否定为 .
3.D【详解】对于A,函数 的定义域为 , 的定义域为 ,两个函数的定义域不同,
所以不是同一个函数,所以A不符合题意;对于B,函数 , ,所以两个函数的对
应关系不同,所以不是同一个函数,所以B不符合题意;对于C,函数 的定义域为 , 的定义
域为 ,两个函数的定义域不同,所以不是同一个函数,所以C不符合题意;
对于D,由函数 与 的定义域与对应关系都相同,所以是同一个函数,所以D符合题意.
4.C【详解】①因数域G是非空数集,取其中任意元素 ,则由数域定义 ,故①正确;②因数域G有
非零元素,设为 ,则由数域定义 ,因 ,则 , ,
类推可得任意正整数都在数域中,故②正确;
③ 表示全体被3整除的整数,则 ,但 ,故③错误;
④设 ,则 , , ,当 时, ,则有理数集是一个数域,故④正确.
5.B【详解】由题意 可变形为
,
即 ,
化简可得 恒成立,
所以 恒成立,
化简可得 ,
解得 ,
所以实数 的取值范围为 ,6.A【详解】∵正实数x,y满足 , ,
∴ ,当且仅当 取等,
设 ,∴ ,
∴ ,即 , ,∴ ,
故 的最小值为2.
7.B【详解】由已知得, 中必有 个正数,1个负数,
设 , ,则 ,
因为 ,所以 ,
所以 ,即 ,
所以 ,由 得, ,即 ,
所以 ,
8.C【详解】对A,由不等式 的解集为 可知 ,A错误;
对B,又2和3是方程 的两根,由韦达定理可得 ,
即 ,所以 ,
解得 ,B错误;
对C, ,C正确;
对D, ,解得 ,D错误.
9.AD【详解】对于A,命题 的否定是 ,故A正确;
对于B,由 可知由两种情况,① 且 ;② ,
故 不能推出 ,由 也不能推出 ,
所以 是 的既不充分也不必要条件,故B错误;对于C,当x=0时, ,故 错误;
对于D,关于 的方程 有一正一负根,则 ,解得 .
所以" "是"关于 的方程 有一正一负根"的充要条件,故D正确.
10.CD【详解】 时, 时, ,
时, , 时, ,
时, , 时, ,
,集合 的非空真子集有 个,所以A,B错误.
又若“ ”是“ ”的充分不必要条件,则 是 的真子集,所以 ,C正确.
若 ,则 时, ;
时, ,
综上 , D正确.
11.ABC【详解】因为关于 的不等式 的解集是 ,
所以 ,且 、 是关于 的方程 即 的两根,
所以 ,故A、B正确,
又 ,
所以 ,故C正确;
又 与 轴有两个交点 , ,
而 是将函数 向上平移一个单位得到,
所以 与 轴的交点横坐标 , ,
所以 ,故D错误;
12.
【详解】根据题意可得“ ”是真命题,当 ,即 时,命题成立;
当 时,得 ,解得 ,
综上,符合题意的实数 的取值范围是 .
13.
【详解】由题意,集合 ,
若 时,集合 ,满足题意;
若 时,要使得集合 ,
则满足 ,解得 ,
综上可得,实数 的取值范围是 .
14.
【详解】因为不等式 的解集为{x|−1≤x≤3},
所以二次函数 的对称轴为直线 ,
且需满足 ,即 ,解得 ,
所以 ,所以 ,
所以 .
15.(1) ; (2) .
【详解】(1)因为命题:“ ,使得 ”为真命题,
所以 ,
即 ,解得 ,
所以集合 ;
(2)因为 ,所以 ,
因为 ,非空集合 ,所以 ,解得 ,
实数 的取值范围为 .
16.(1) , (2) 在 上单调递增,在 上单调递减
(3)证明见解析
【详解】(1)解:由 ,均有 且 ,
令 ,可得 ,
令 ,可得 .
因为曲线 与ℎ(x)恰有一个交点且交点横坐标为 ,所以 ,
又因为曲线 与ℎ(x)恰有一个交点,所以 有两个相等的实数根,
则 ,
因为 ,可得 ,解得 ,
所以 ,则 .
(2)函数 在(0,1)上单调递增,在(1,+∞)上单调递减.
设 且 ,
则
,
其中
当 时, ,则 ,即 ,
此时函数 在(0,1)上单调递增;
当 时, ,则 ,即 ,
此时函数 在(1,+∞)上单调递减,
所以函数 在(0,1)上单调递增,在(1,+∞)上单调递减.(3)证明:因为 ,
由 ,可得 ,即 ,
所以 ,整理得 ,
又因为 ,由基本不等式,可得 .
17.(1)采用方案二;理由见解析 (2)24
【详解】(1)解:方案一的总费用为 (元);
方案二的总费用为 (元),
由 ,
因为 ,可得 ,所以 ,
即 ,所以 ,所以采用方案二,花费更少.
(2)解:由(1)可知 ,
令 ,则 ,
所以 ,当 时,即 时,等号成立,
又因为 ,可得 ,
所以 ,
当且仅当 时,即 时,等号成立,
所以差 的最小值为 ,当且仅当 时,等号成立,
所以两种方案花费的差值 最小为24元.
18.(1) (2)
【详解】(1)命题 为假命题,则 : , 为真命题.
得 或 ;
(2)由(1)若命题 为假命题,则 ,则若其为真命题,则 ;
若命题 为真命题,则 ,
则若命题 为假命题,则 .
又命题 和 中有且仅有一个是假命题,则命题 和 一真一假.
若 真 假,则 ;
若 假 真,则 .
综上, .
19.(1)
(2)当 时, 解集为 ;
当 时, 解集为 ;
当 时, 解集为 .
(3)
【详解】(1)由题意,
当 , 即 时, , 解集不为 , 不合题意;
当 , 即 时, 的解集为 ,
,即
故 时, .
综上, .
(2)由题意得,
在 , 即 ,当 , 即 时, 解集为 ;
当 , 即 时, ,
即 解集为 ;
当 , 即 时, ,
解集为 .
综上,当 时, 解集为 ;
当 时, 解集为 ;
当 时, 解集为 .
(3)由题意,
, 即 ,
恒成立,
∴ ,
设 , 则
,
, 当且仅当 时取等号,
, 当且仅当 时取等号,
当 时, ,
,
∴ 的取值范围为 .