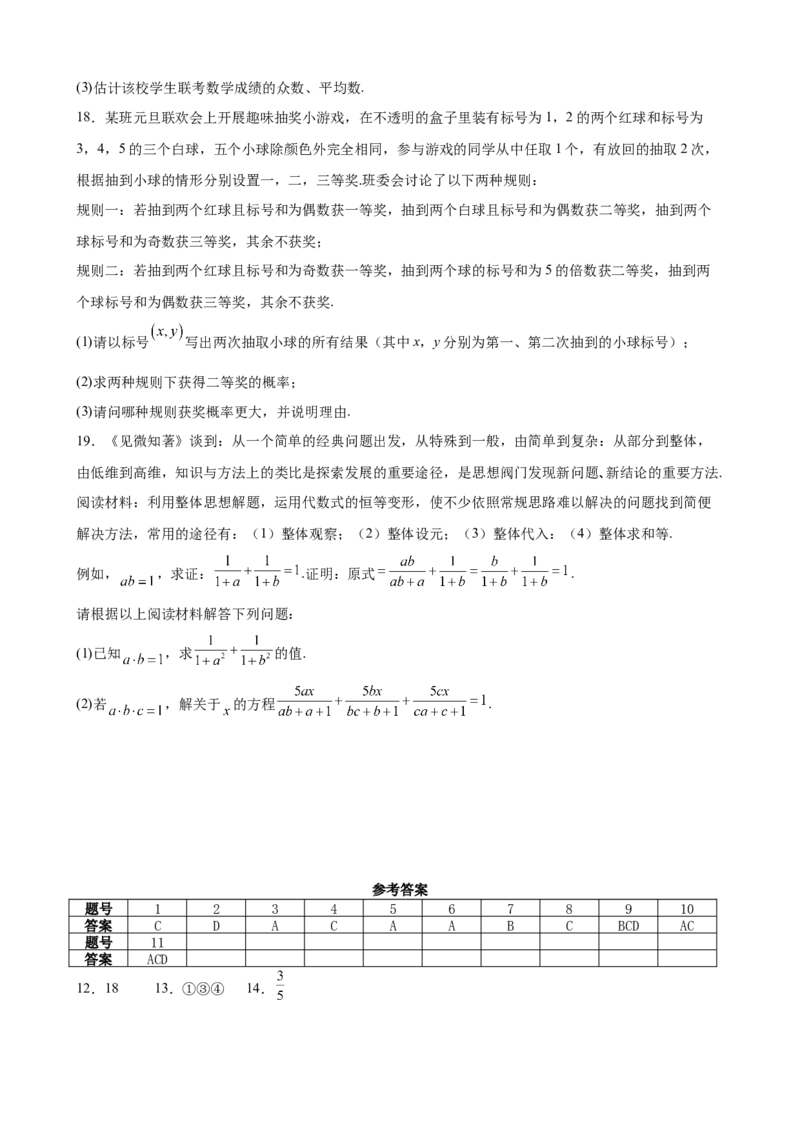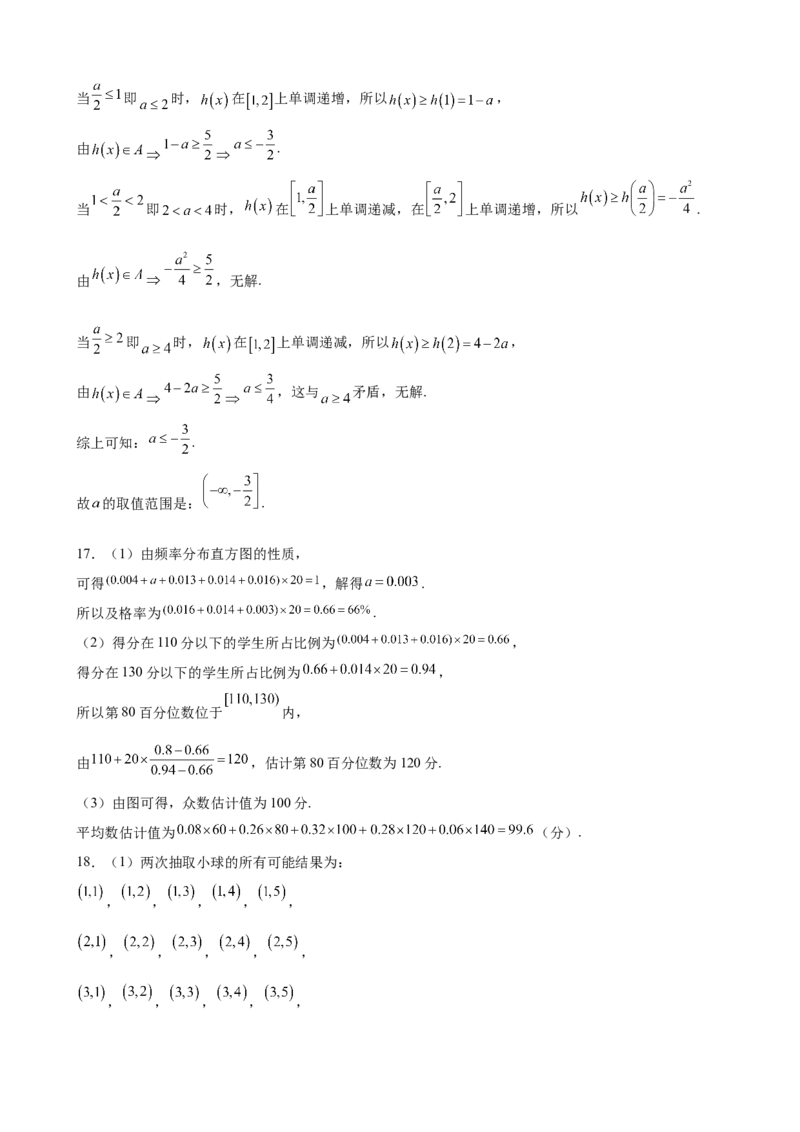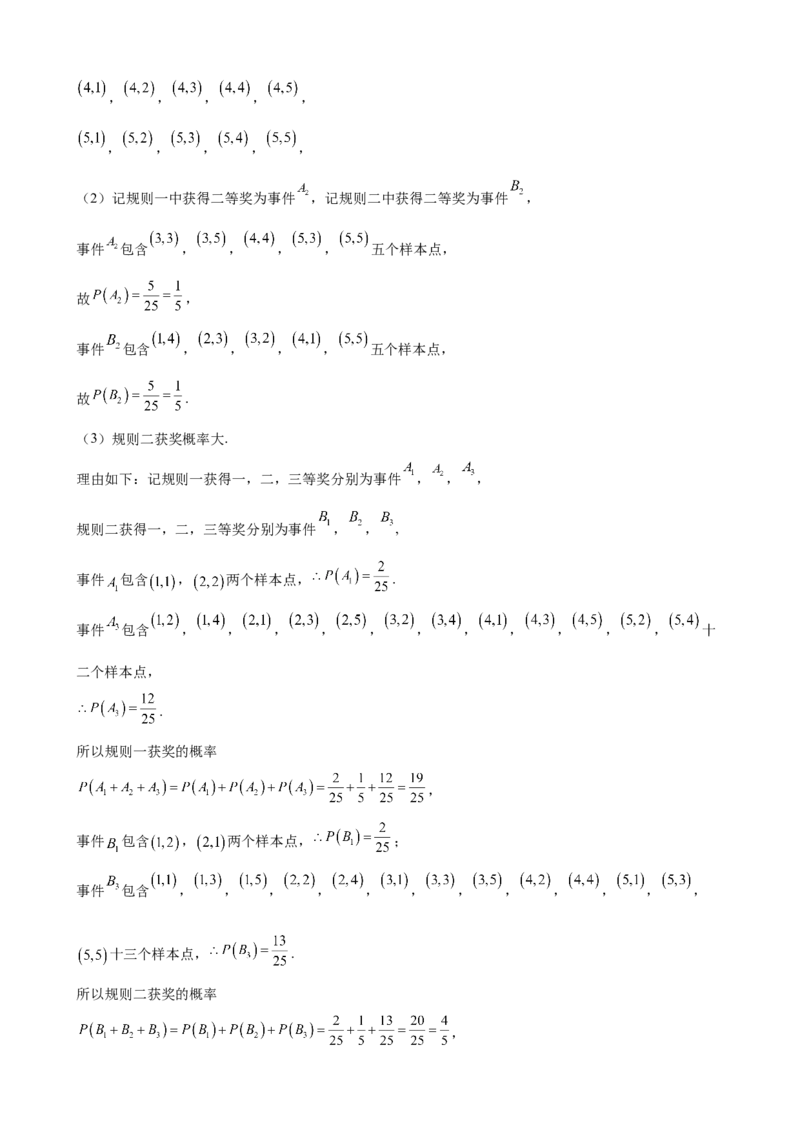文档内容
新蔡县第一高级中学 2024-2025 学年高一下学期 3 月份月考数学试题
一、单选题
1.已知 ,则函数 的解析式为( )
A. B.
C. D.
2.已知 ,则 的最小值为( )
A. B. C. D.
3.若函数 在区间 上单调递增,则实数 的取值范围是( )
A. B. C. D.
4.已知数据87,89,90,90,91,92,93,94,则( )
A.极差为6 B.中位数为90
C.第70%分位数为92 D.平均数为90.25
5.现有甲,乙两支篮球队进行比赛,甲队每场获胜的概率为 ,且各场比赛互不影响.若比赛采用“三
局两胜”制,则甲队获得胜利的概率为( )
A. B. C. D.
6.函数 的图象大致为( )
A. B.
C. D.7.设集合 ,那么( )
A. B. C. D.
8.如图所示,两动点 在以坐标原点 为圆心,半径为1的圆上从点 处同时出发做匀速圆周运
动.已知点 按逆时针方向每秒钟转 弧度,点 按顺时针方向每秒钟转 弧度 ,且
两点在第2秒末第一次相遇于点 处,则它们从出发后到第2次相遇时,点 走过的总路程为
( )
A. B. C. D.
二、多选题
9.在平面直角坐标系 中,已知角 的终边经过点 ,下列说法正确的有( )
A. B.
C. D.
10.下列关于角 的说法正确的是( )
A.终边在第二象限的角的集合为
B.与 终边相同的角的集合为
C.若角 ,则角 是第四象限角D.若角 是三角形的一个内角,则角 必是第一、二象限角
11.已知函数 ,则方程 的根的个数可能为( )
A.2 B.6 C.5 D.4
三、填空题
12. .
13.生态学研究发现:当种群数量较少时,种群近似呈指数增长,而当种群增加到一定数量后,增长率
就会随种群数量的增加而逐渐减小.为了刻画这种现象,生态学上提出了著名的逻辑斯蒂模型:
,其中 是正常数, 表示初始时刻种群数量, 叫做种群的内秉增长率,
是环境容纳量. 可以近似刻画 时刻的种群数量.给出下列四个结论: 如果 ,那么存在
①
;
如果 ,那么存在 ;
②
如果 ,那么对任意 ;
③
如果 ,那么存在 ,任意 .
④
其中所有正确结论的序号是 .
14.中国传统折扇文化有着极其深厚的底蕴,“数摺聚清风,一捻生秋意”是宋朝朱翌描写折扇的诗句.
如图,假设这把折扇是从一个圆面中剪下的扇形制作而成,制作扇子的扇形面积为 ,圆面中剩余部分
的面积为 .当扇子扇形的圆心角的度数为 时,扇面看上去形状较为美观,则此时 .四、解答题
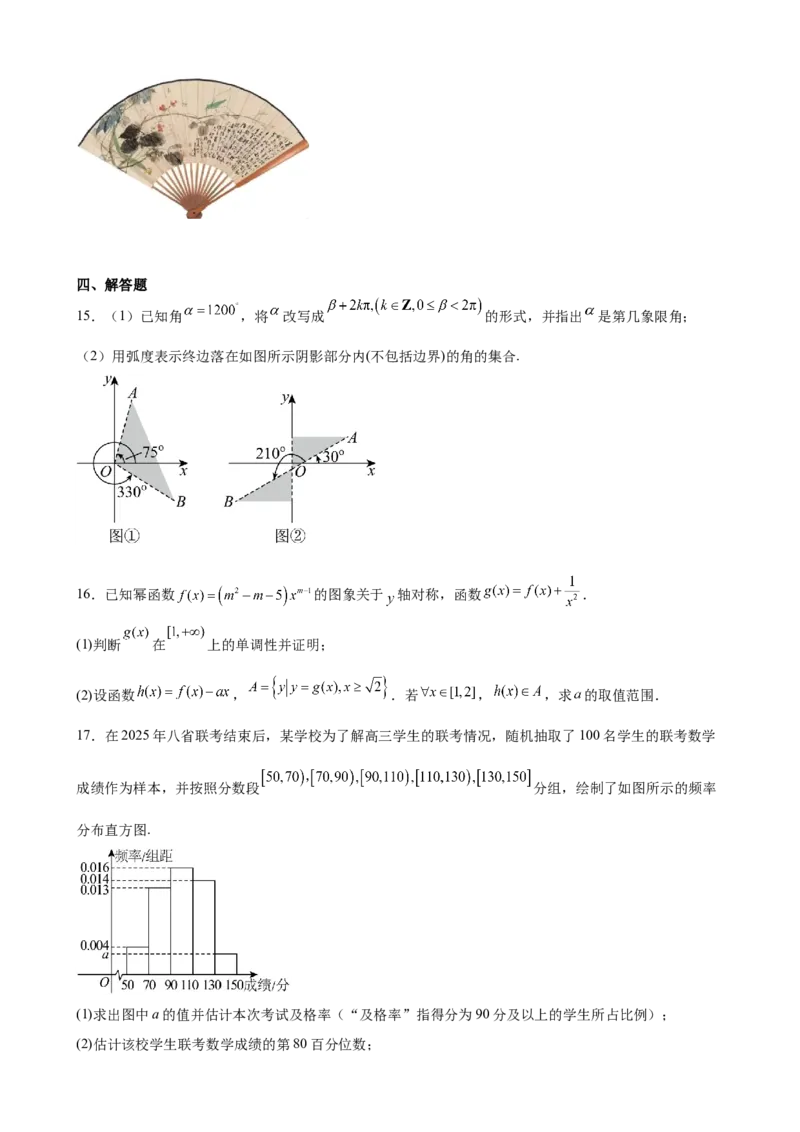
15.(1)已知角 ,将 改写成 的形式,并指出 是第几象限角;
(2)用弧度表示终边落在如图所示阴影部分内(不包括边界)的角的集合.
16.已知幂函数 的图象关于 轴对称,函数 .
(1)判断 在 上的单调性并证明;
(2)设函数 , .若 , ,求 的取值范围.
17.在2025年八省联考结束后,某学校为了解高三学生的联考情况,随机抽取了100名学生的联考数学
成绩作为样本,并按照分数段 分组,绘制了如图所示的频率
分布直方图.
(1)求出图中a的值并估计本次考试及格率(“及格率”指得分为90分及以上的学生所占比例);
(2)估计该校学生联考数学成绩的第80百分位数;(3)估计该校学生联考数学成绩的众数、平均数.
18.某班元旦联欢会上开展趣味抽奖小游戏,在不透明的盒子里装有标号为1,2的两个红球和标号为
3,4,5的三个白球,五个小球除颜色外完全相同,参与游戏的同学从中任取1个,有放回的抽取2次,
根据抽到小球的情形分别设置一,二,三等奖.班委会讨论了以下两种规则:
规则一:若抽到两个红球且标号和为偶数获一等奖,抽到两个白球且标号和为偶数获二等奖,抽到两个
球标号和为奇数获三等奖,其余不获奖;
规则二:若抽到两个红球且标号和为奇数获一等奖,抽到两个球的标号和为5的倍数获二等奖,抽到两
个球标号和为偶数获三等奖,其余不获奖.
(1)请以标号 写出两次抽取小球的所有结果(其中x,y分别为第一、第二次抽到的小球标号);
(2)求两种规则下获得二等奖的概率;
(3)请问哪种规则获奖概率更大,并说明理由.
19.《见微知著》谈到:从一个简单的经典问题出发,从特殊到一般,由简单到复杂:从部分到整体,
由低维到高维,知识与方法上的类比是探索发展的重要途径,是思想阀门发现新问题、新结论的重要方法.
阅读材料:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便
解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入:(4)整体求和等.
例如, ,求证: .证明:原式 .
请根据以上阅读材料解答下列问题:
(1)已知 ,求 的值.
(2)若 ,解关于 的方程 .
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D A C A A B C BCD AC
题号 11
答案 ACD
12.18 13.①③④ 14.15.(1)因为 ,
所以角 与 的终边相同,且 ,所以角 是第二象限角;
(2)图①:因为 ,
所以阴影部分内(不包括边界)的角的集合 ;
图②:因为 ,
所以阴影部分内(不包括边界)的角的集合 .
16.(1)由 ,所以 或 ,
由幂函数 的图象关于 轴对称,所以 .
故 .所以 .
函数 在 上单调递增,下面用单调性定义证明:设 ,
则 .
因为 ,所以 , , ,所以 ,
所以 ,即 .
所以函数 在 上单调递增.
(2)因为函数 在 上单调递增,且 ,
所以 , .
对 , .当 即 时, 在 上单调递增,所以 ,
由 .
当 即 时, 在 上单调递减,在 上单调递增,所以 .
由 ,无解.
当 即 时, 在 上单调递减,所以 ,
由 ,这与 矛盾,无解.
综上可知: .
故 的取值范围是: .
17.(1)由频率分布直方图的性质,
可得 ,解得 .
所以及格率为 .
(2)得分在110分以下的学生所占比例为 ,
得分在130分以下的学生所占比例为 ,
所以第80百分位数位于 内,
由 ,估计第80百分位数为120分.
(3)由图可得,众数估计值为100分.
平均数估计值为 (分).
18.(1)两次抽取小球的所有可能结果为:
, , , , ,
, , , , ,
, , , , ,, , , , ,
, , , , ,
(2)记规则一中获得二等奖为事件 ,记规则二中获得二等奖为事件 ,
事件 包含 , , , , 五个样本点,
故 ,
事件 包含 , , , , 五个样本点,
故 .
(3)规则二获奖概率大.
理由如下:记规则一获得一,二,三等奖分别为事件 , , ,
规则二获得一,二,三等奖分别为事件 , , ,
事件 包含 , 两个样本点, .
事件 包含 , , , , , , , , , , , 十
二个样本点,
.
所以规则一获奖的概率
,
事件 包含 , 两个样本点, ;
事件 包含 , , , , , , , , , , , ,
十三个样本点, .
所以规则二获奖的概率
,,∴所以规则二获奖的概率大.
19.(1)已知 ,则有 .
(2)由 ,
关于 的方程 ,
可化为: ,
即: ,
∴ ,即 ,解得: .