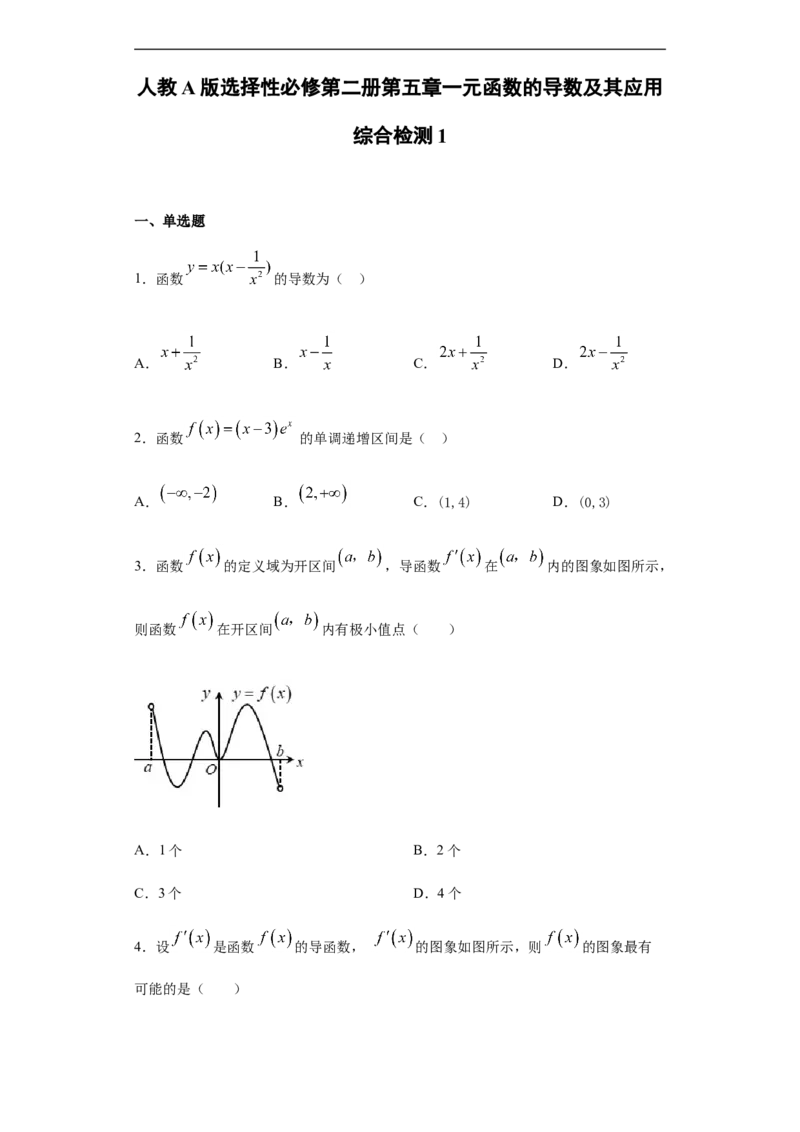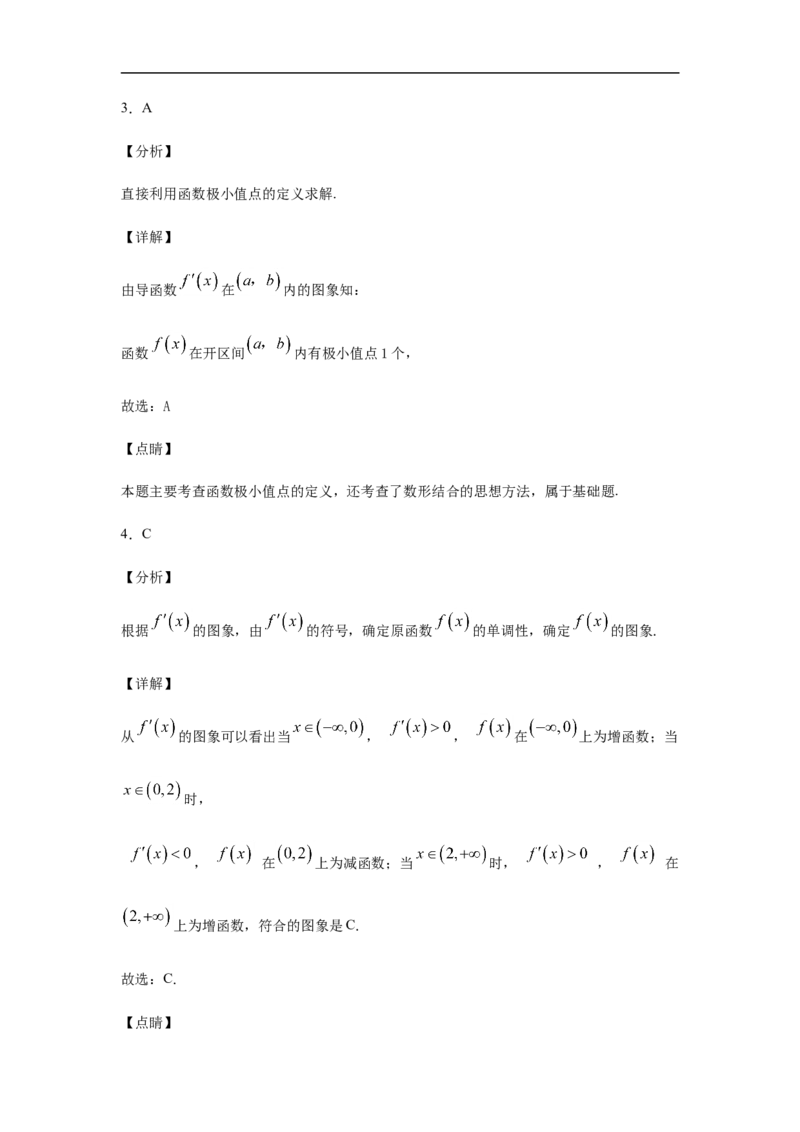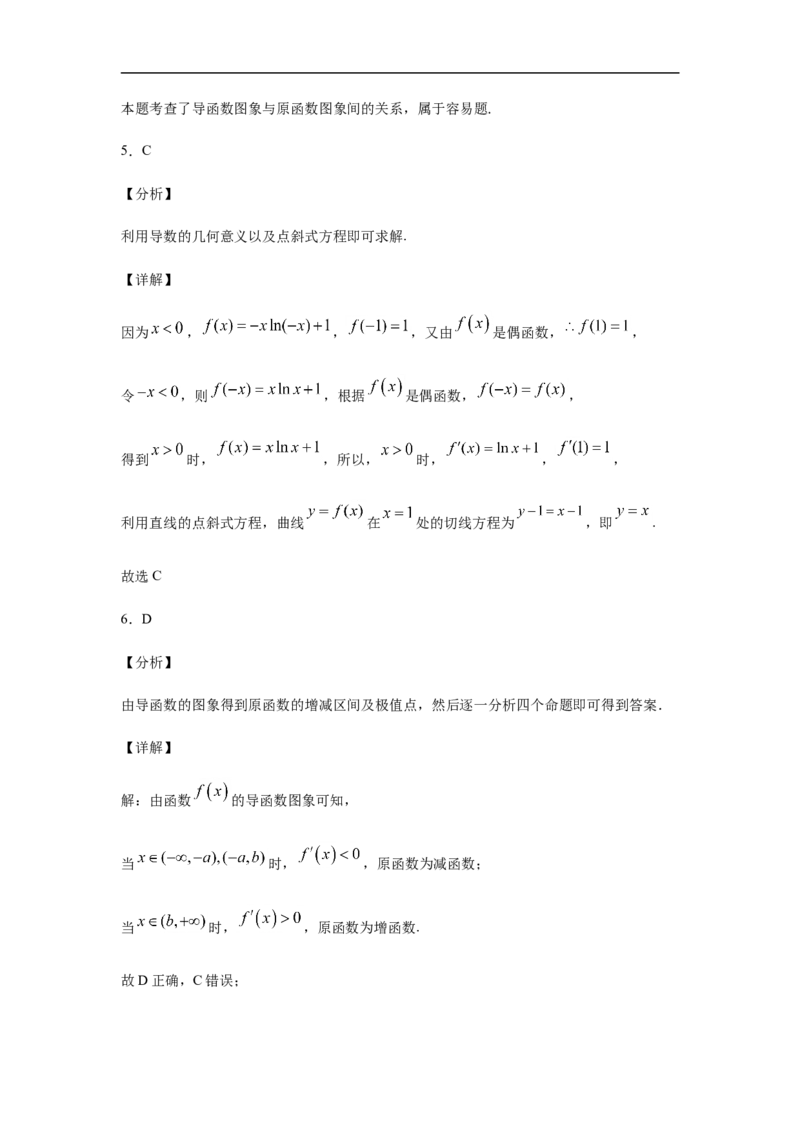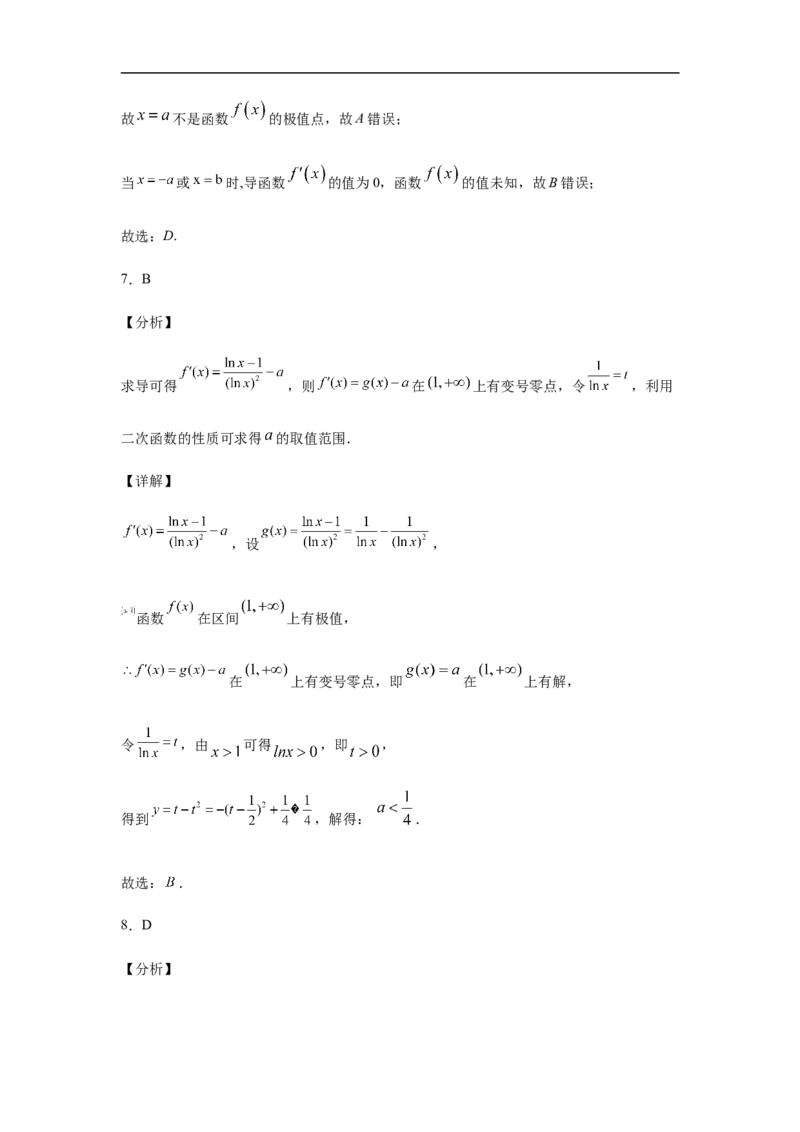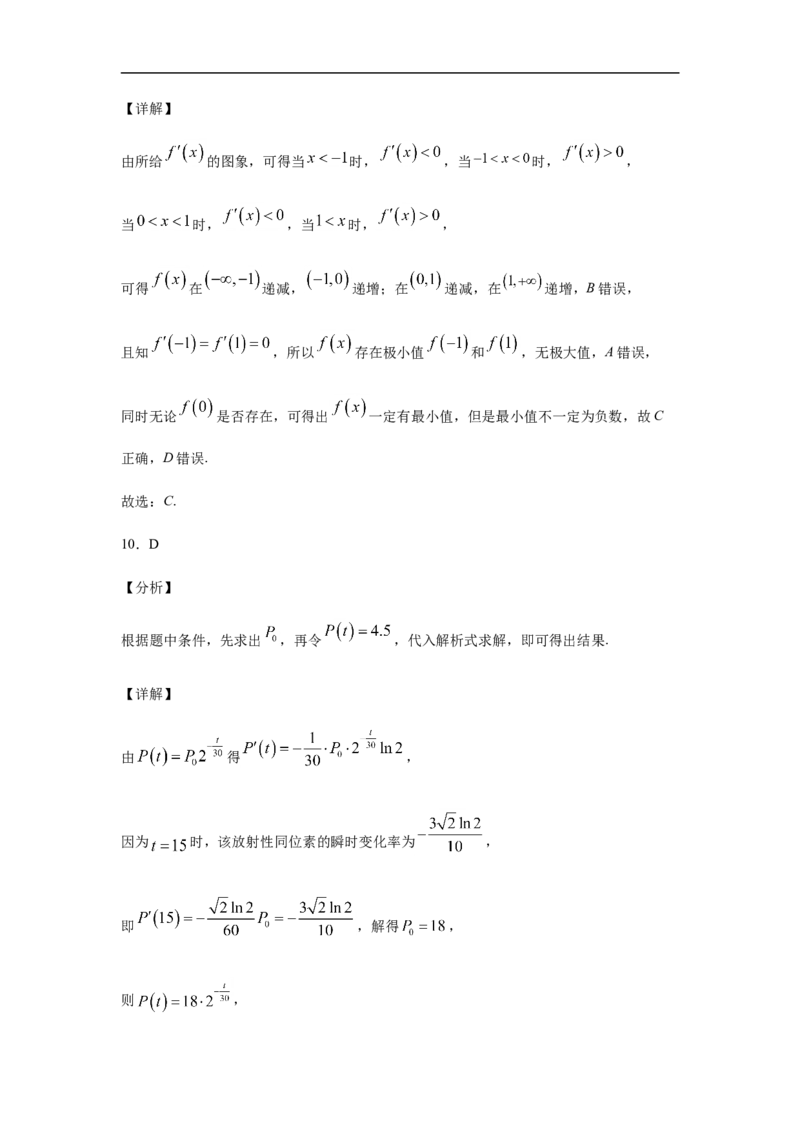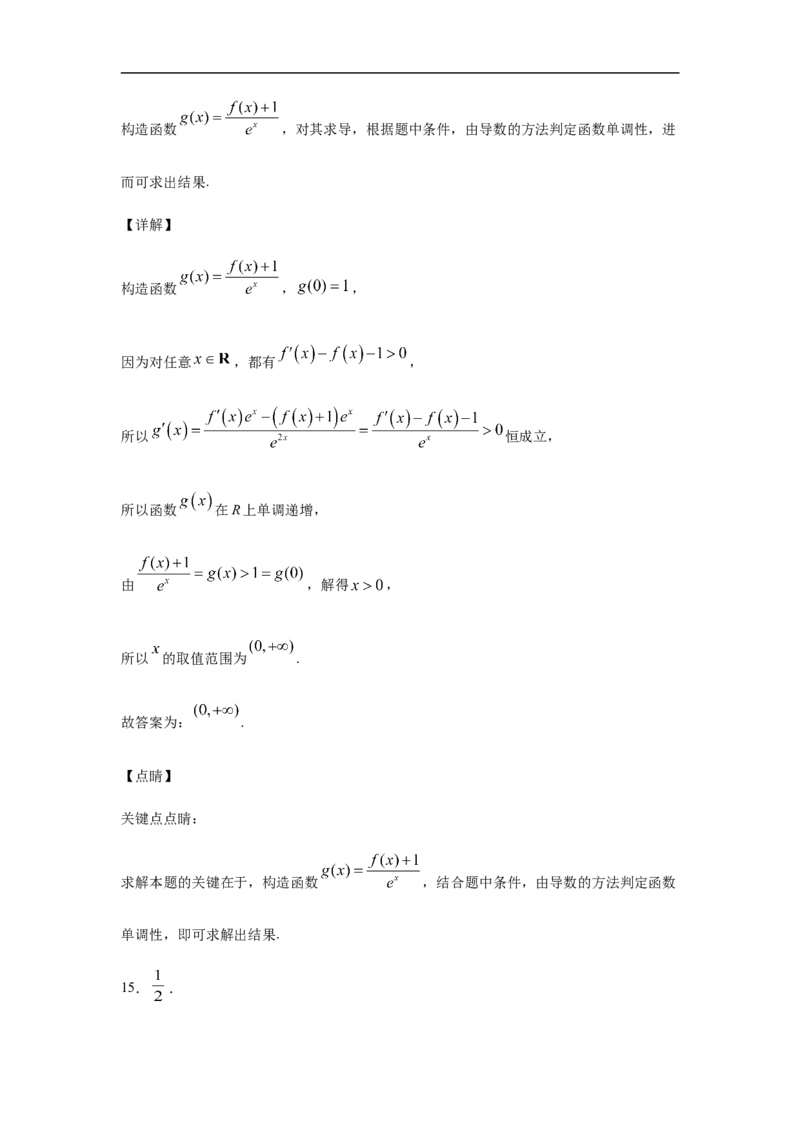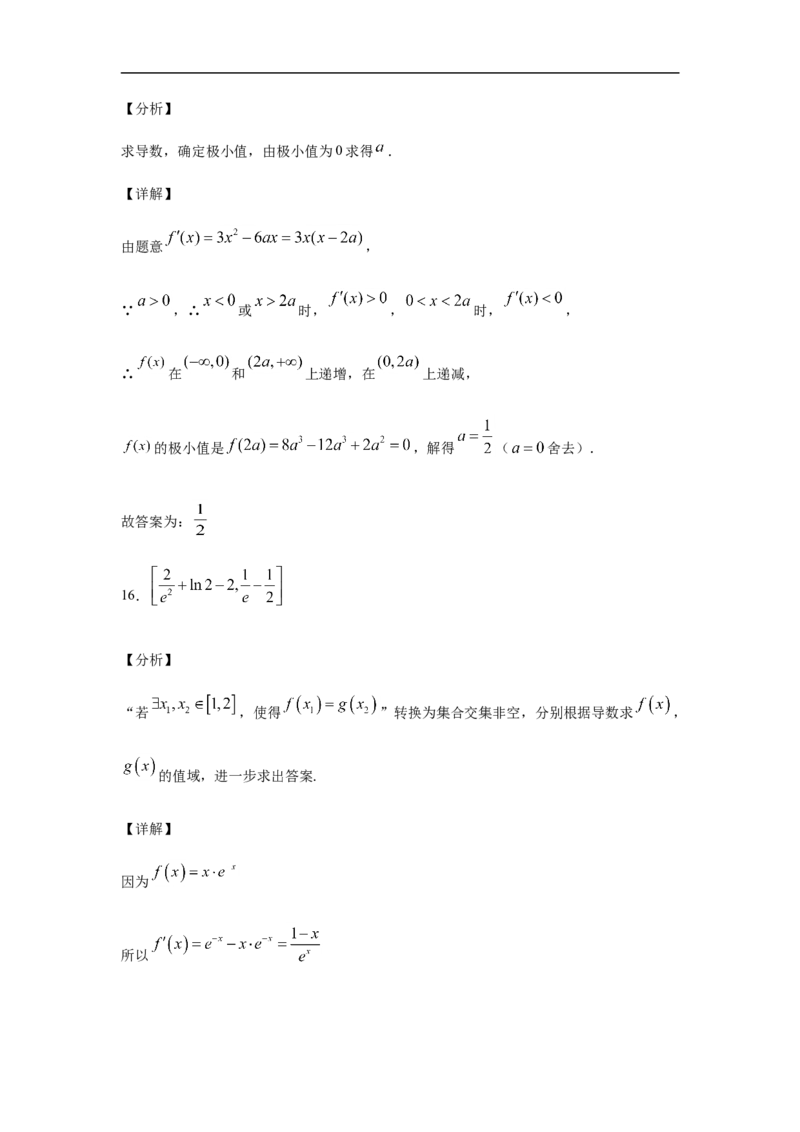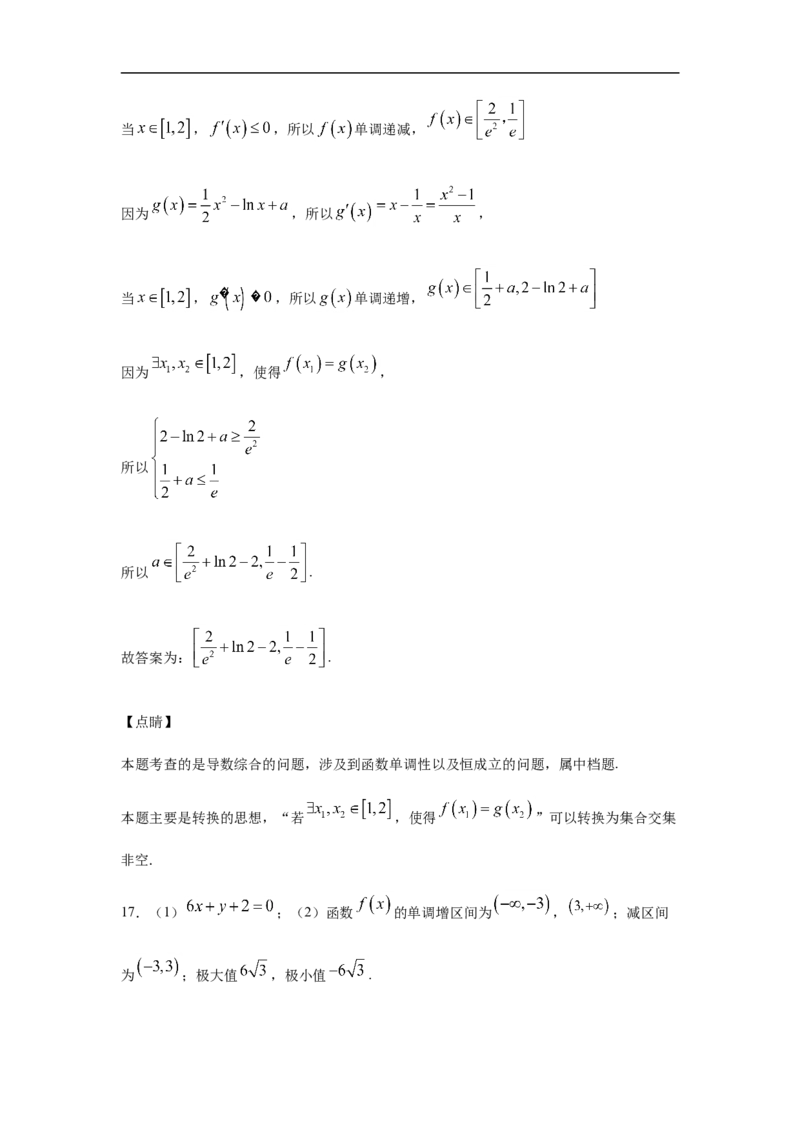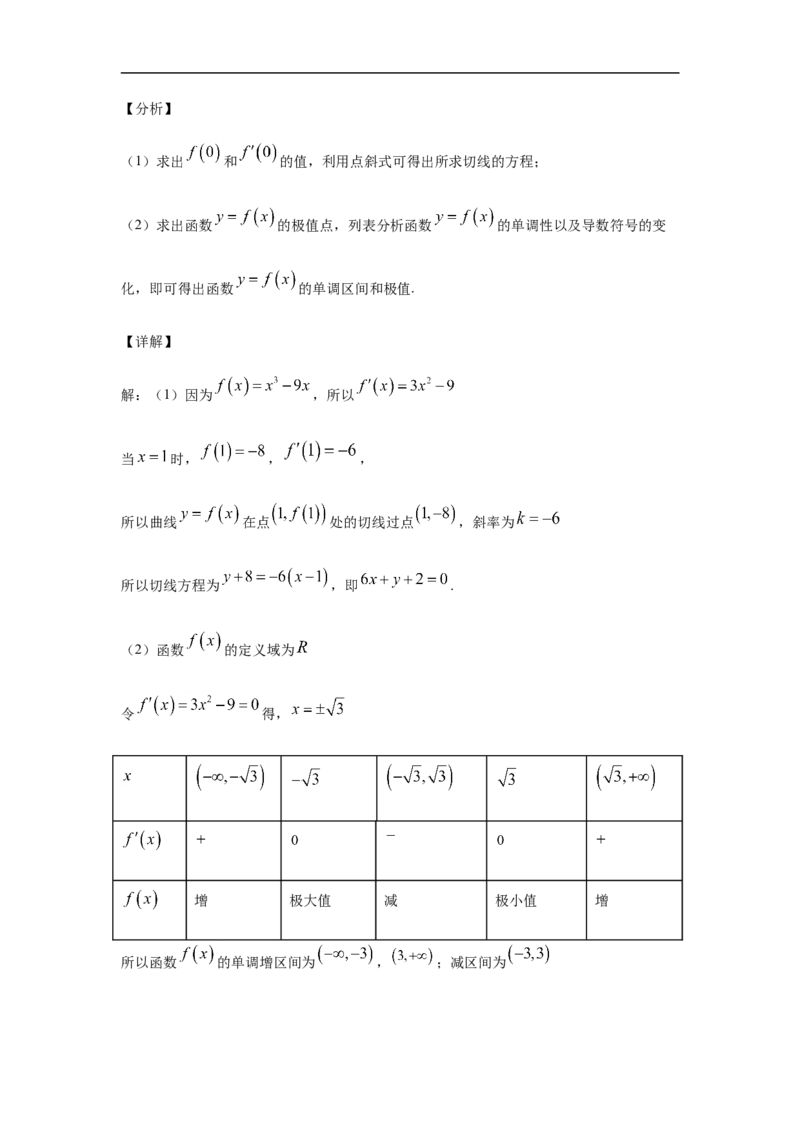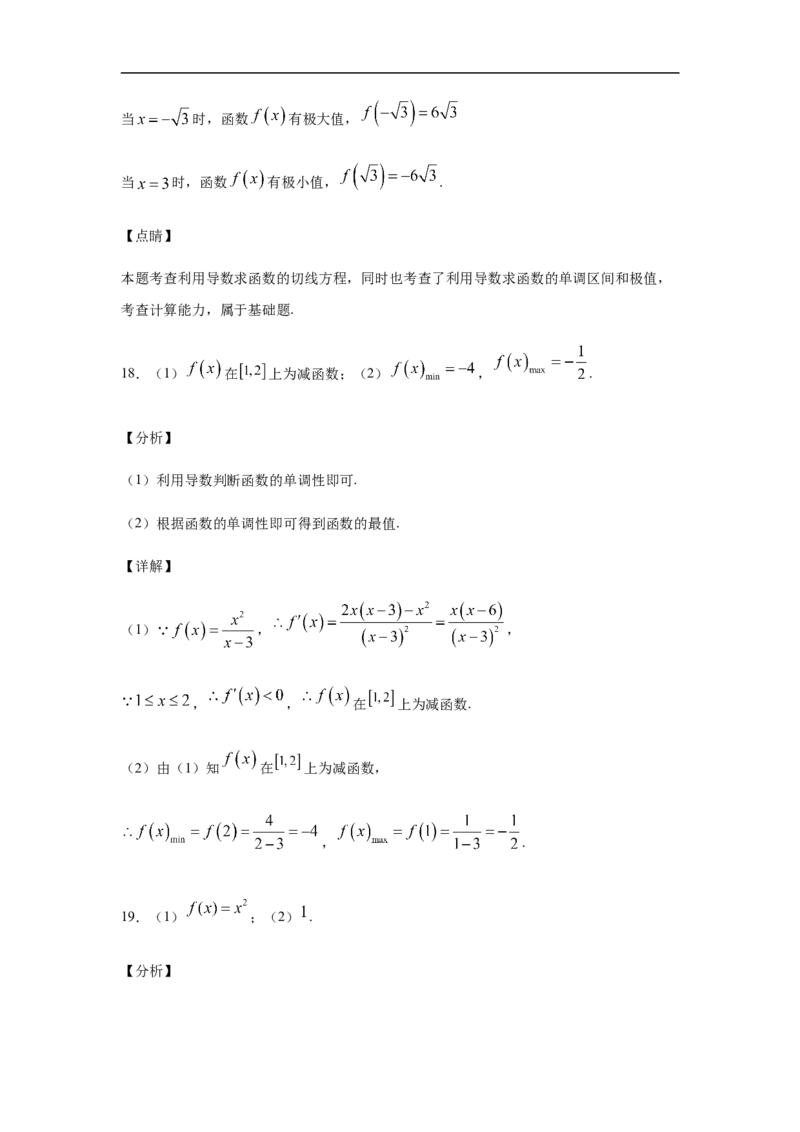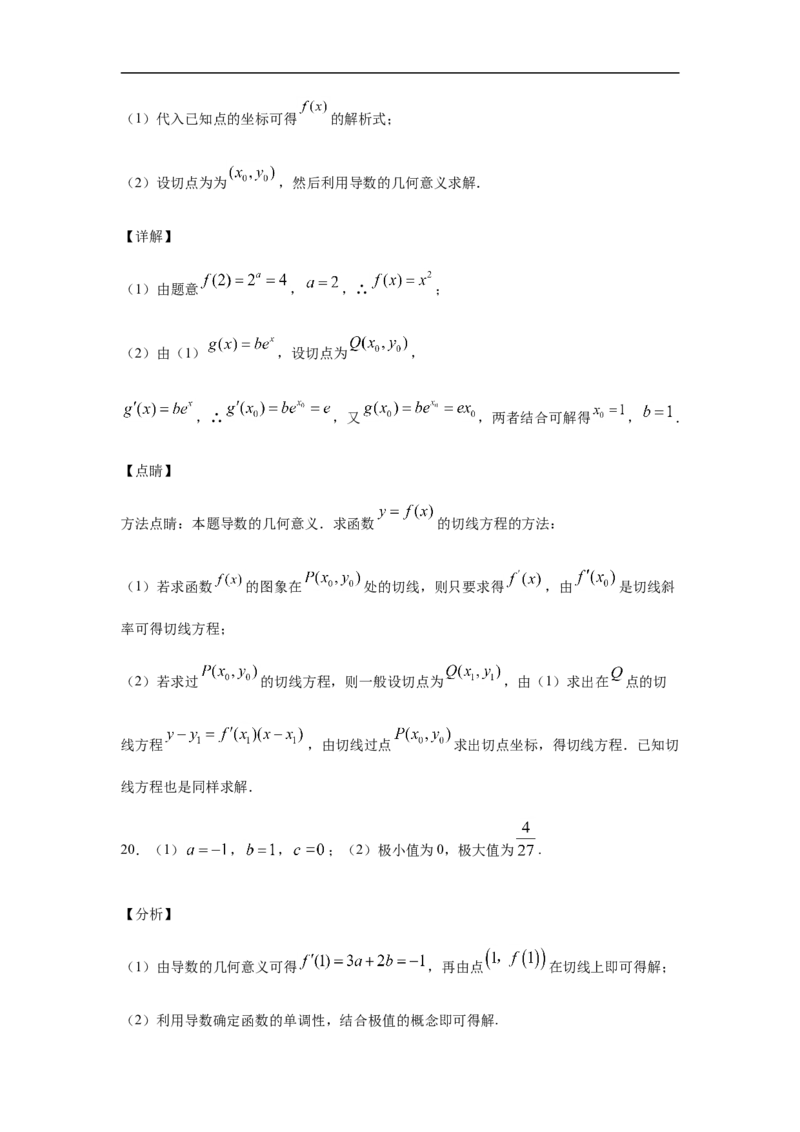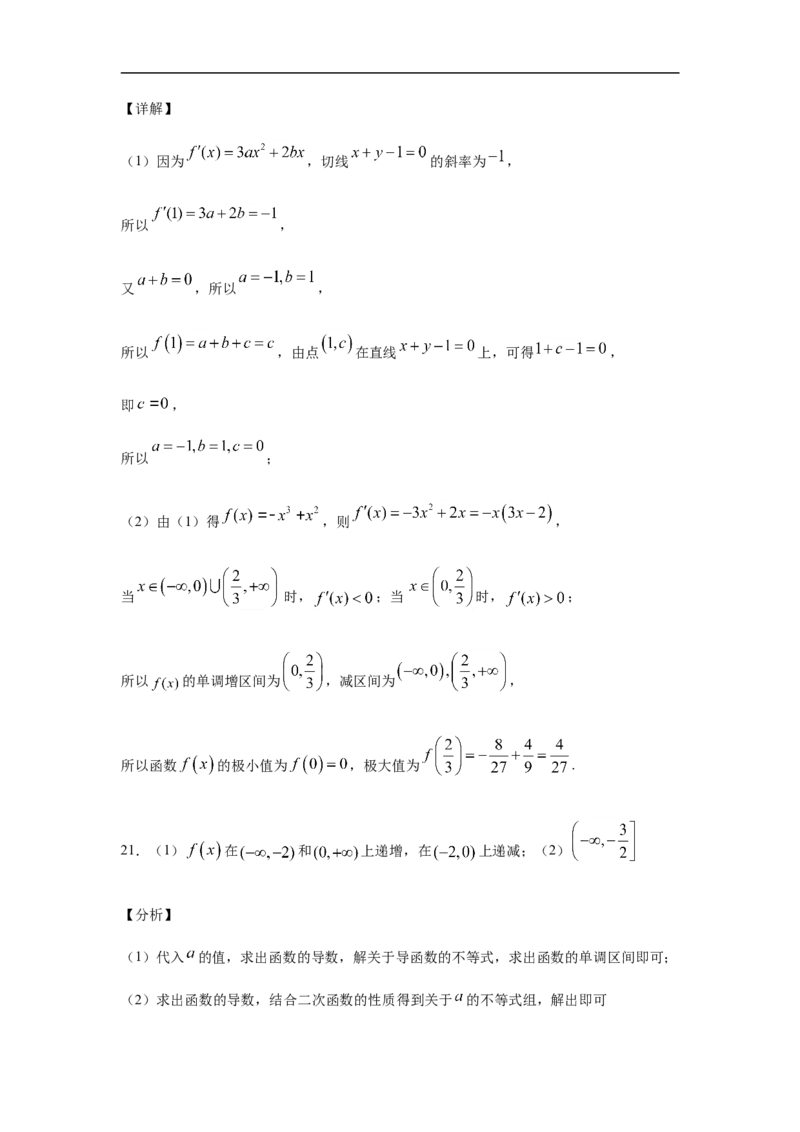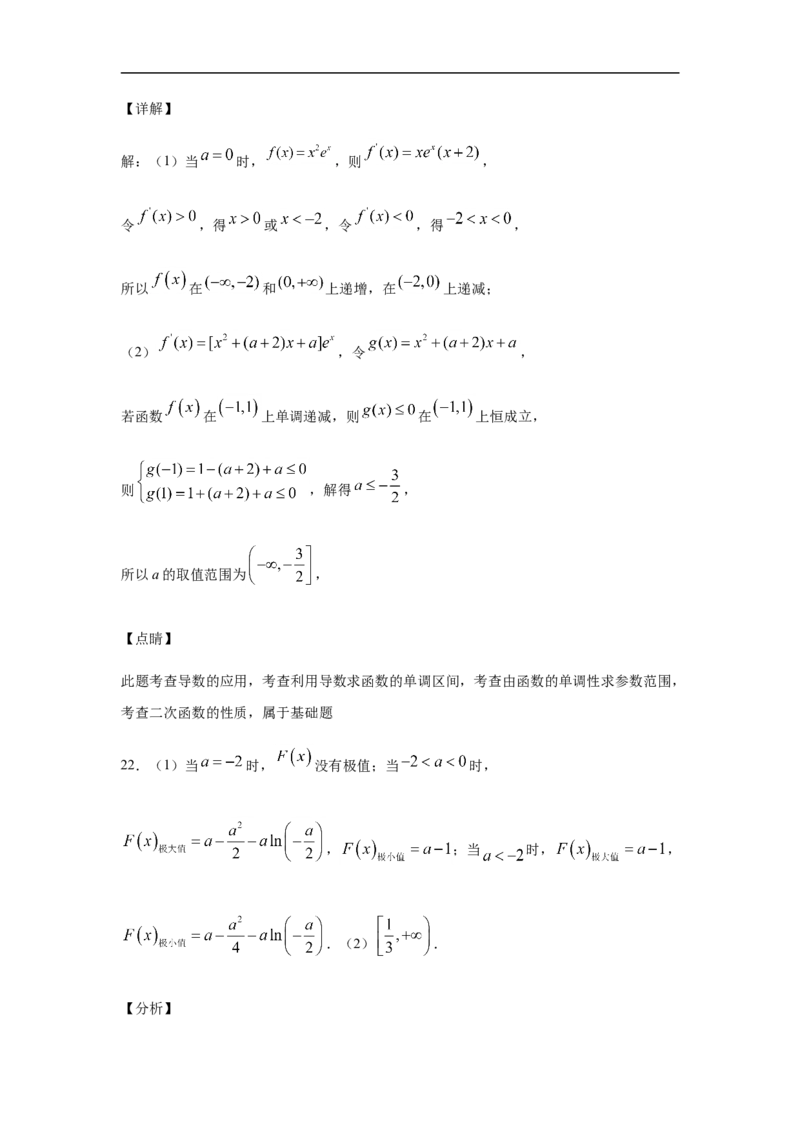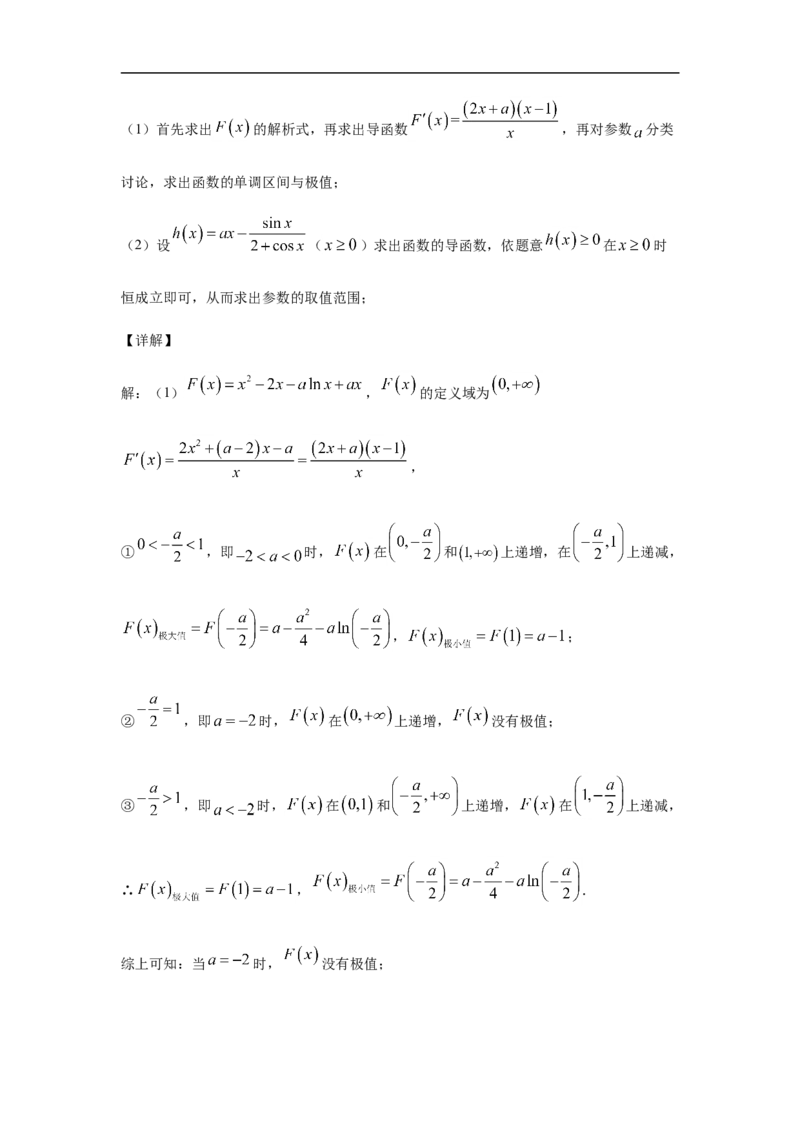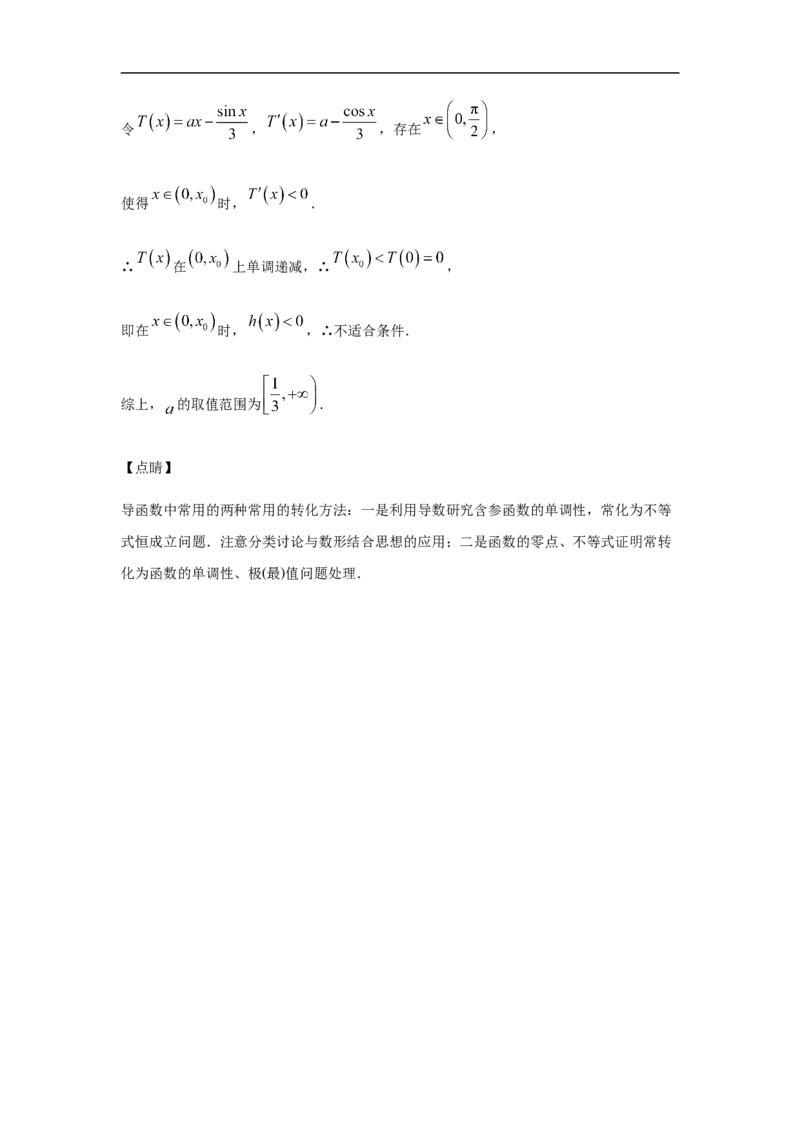文档内容
人教A版选择性必修第二册第五章一元函数的导数及其应用
综合检测1
一、单选题
1.函数 的导数为( )
A. B. C. D.
2.函数 的单调递增区间是( )
A. B. C.(1,4) D.(0,3)
3.函数 的定义域为开区间 ,导函数 在 内的图象如图所示,
则函数 在开区间 内有极小值点( )
A.1个 B.2个
C.3个 D.4个
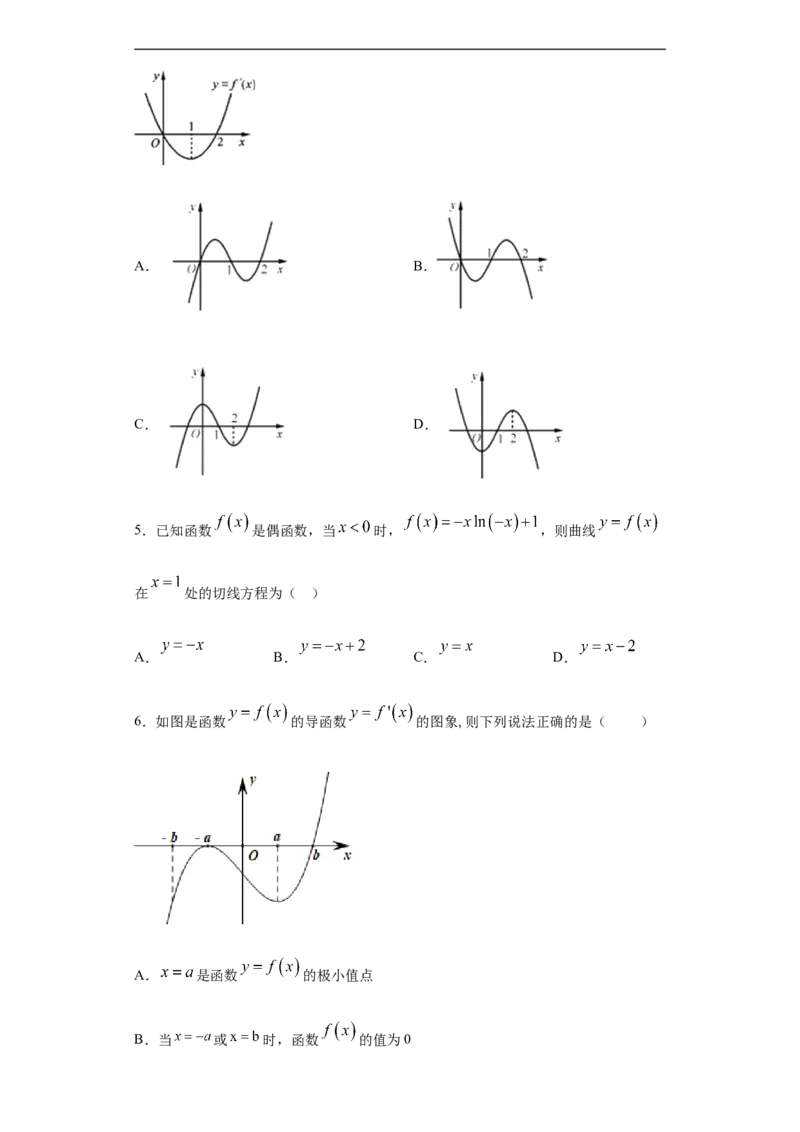
4.设 是函数 的导函数, 的图象如图所示,则 的图象最有
可能的是( )A. B.
C. D.
5.已知函数 是偶函数,当 时, ,则曲线
在 处的切线方程为( )
A. B. C. D.
6.如图是函数 的导函数 的图象,则下列说法正确的是( )
A. 是函数 的极小值点
B.当 或 时,函数 的值为0C.函数 在 上是增函数
D.函数 在 上是增函数
7.已知函数 在 上有极值,则实数 的取值范围为( )
A. B. C. D.
8.已知函数 , ,则下列判断正确的是( )
A. 是增函数 B. 的极大值点是
C. 是减函数 D. 的极小值点是
9.函数 的导函数为 ,若已知 图象如图,则下列说法正确的是(
)
A. 存在极大值点 B. 在 单调递增
C. 一定有最小值 D.不等式 一定有解
10.随着科学技术的发展,放射性同位素技术已经广泛应用于医学、航天等众多领域,并取得了显著经济效益.假设某放射性同位素的衰变过程中,其含量 (单位:贝克)
与时间 (单位:天)满足函数关系 ,其中 为时该放射性同位素的含
量.已知 时,该放射性同位素的瞬时变化率为 ,则该放射性同位素含
量为 贝克时衰变所需时间为( )
A.20天 B.30天 C.45天 D.60天
11.已知定义在 上的函数 满足 ,其中 是函数
的导函数,若 ,则实数 的取值范围为(
)
A. B. C. D.
12.已知函数 是定义在R上的可导函数,对于任意的实数x,都有 ,
当 时, ,若 ,则实数a的取值范围是
( )
A. B. C. D.
第II卷(非选择题)
请点击修改第II卷的文字说明二、填空题
13.曲线 在点 处的切线的方程为__________.
14.定义在R上的函数 的导函数为 , ,若对任意 ,都有
,则使得 成立的 的取值范围为______.
15.已知 为正实数,若函数 的极小值为0,则 的值为_____
16.已知函数 , ,若 ,使得
,则实数 的取值范围是______.
三、解答题
17.已知函数 .
(1)求曲线 在点 处的切线方程;
(2)求函数 的单调区间与极值.
18.已知函数 .
(1)试判断 在 上的单调性;
(2)求函数 在 上的最值.19.已知函数 经过点 , .
(1)求函数 的解析式;
(2)设函数 ,若 的图象与直线 相切,求 值.
20.设函数 ,其中 , , , 均为常数,曲线
在 处的切线方程为 .
(1)求 , , 的值;
(2)求函数 的极值.
21.已知 ,函数 .
(1)当 时,求函数 的单调区间;
(2)若函数 在 上单调递减,求a的取值范围.
22.已知函数 , .
(1)若 为负实数, 求函数 的极值;
(2)若不等式 对 恒成立,求 的取值范围.参考答案
1.C
【分析】
直接利用导数的运算公式和法则求解.
【详解】
因为函数 ,
所以 ,
故选:C
【点睛】
本题主要考查函数的导数的计算,属于基础题.
2.B
【分析】
求出函数 的导数,在解出不等式 可得出所求函数的单调递增区间.
【详解】
, ,解不等式 ,解得 ,
因此,函数 的单调递增区间是 ,故选B.
【点睛】
本题考查函数单调区间的求解,一般是先求出导数,然后解出导数不等式,将解集与定义
域取交集得出单调区间,但单调区间不能合并,考查计算能力,属于中等题.3.A
【分析】
直接利用函数极小值点的定义求解.
【详解】
由导函数 在 内的图象知:
函数 在开区间 内有极小值点1个,
故选:A
【点睛】
本题主要考查函数极小值点的定义,还考查了数形结合的思想方法,属于基础题.
4.C
【分析】
根据 的图象,由 的符号,确定原函数 的单调性,确定 的图象.
【详解】
从 的图象可以看出当 , , 在 上为增函数;当
时,
, 在 上为减函数;当 时, , 在
上为增函数,符合的图象是C.
故选:C.
【点睛】本题考查了导函数图象与原函数图象间的关系,属于容易题.
5.C
【分析】
利用导数的几何意义以及点斜式方程即可求解.
【详解】
因为 , , ,又由 是偶函数, ,
令 ,则 ,根据 是偶函数, ,
得到 时, ,所以, 时, , ,
利用直线的点斜式方程,曲线 在 处的切线方程为 ,即 .
故选C
6.D
【分析】
由导函数的图象得到原函数的增减区间及极值点,然后逐一分析四个命题即可得到答案.
【详解】
解:由函数 的导函数图象可知,
当 时, ,原函数为减函数;
当 时, ,原函数为增函数.
故D正确,C错误;故 不是函数 的极值点,故A错误;
当 或 时,导函数 的值为0,函数 的值未知,故B错误;
故选:D.
7.B
【分析】
求导可得 ,则 在 上有变号零点,令 ,利用
二次函数的性质可求得 的取值范围.
【详解】
,设 ,
函数 在区间 上有极值,
在 上有变号零点,即 在 上有解,
令 ,由 可得 ,即 ,
得到 ,解得: .
故选: .
8.D
【分析】求出 求出函数
的单调区间,从而可得出答案.
【详解】
由
由
解得 ,又 ,所以
由 ,得 或
所以 在 上单调递减,在 上单调递增,在 上单调递减.
所以函数 在 上不是单调函数,故A, C不正确.
所以函数 在 处有极小值,在 处有极大值.故选项B不正确,选项D正
确.
故选:D
9.C
【分析】
根据图象可得 的符号,从而可得 的单调区间,再对选项进行逐一分析判断正
误得出答案.【详解】
由所给 的图象,可得当 时, ,当 时, ,
当 时, ,当 时, ,
可得 在 递减, 递增;在 递减,在 递增,B错误,
且知 ,所以 存在极小值 和 ,无极大值,A错误,
同时无论 是否存在,可得出 一定有最小值,但是最小值不一定为负数,故C
正确,D错误.
故选:C.
10.D
【分析】
根据题中条件,先求出 ,再令 ,代入解析式求解,即可得出结果.
【详解】
由 得 ,
因为 时,该放射性同位素的瞬时变化率为 ,
即 ,解得 ,
则 ,当该放射性同位素含量为 贝克时,即 ,
所以 ,即 ,所以 ,解得 .
故选:D.
11.D
【分析】
构造函数 ,根据导数可判断函数单调递减,由 ,结合
函数定义域可解得.
【详解】
令 , ,则 ,
因为 ,所以 ,所以函数 在 上单调递减.
因为 , ,所以 ,
即 ,所以 且 ,解得 ,
所以实数 的取值范围为 .
故选D.
【点睛】
易错点点睛,本题的容易忽略定义域 ,切记解函数抽象不等式要优先考虑定义域.
12.B
【分析】
构造函数 ,根据题意,可得函数 的奇偶性,根据 时
,对函数 求导,可得函数 的单调性,将
,左右同乘 ,可得 ,即
,利用 的性质,即可求得答案.
【详解】
∵ ,∴ ,
令 ,则 ,即 为偶函数,
当 时 ,
∴ ,即函数 在 上单调递增.
根据偶函数对称区间上单调性相反的性质可知 在 上单调递减,
∵ ,
∴ ,
∴ ,即 ,解得, ,
故选:B.
【点睛】
解题的关键是将题干条件转化为 ,根据左右相同的形式,
构造函数 ,再根据题意,求得函数的奇偶性,单调性;难点在于:由于
,不符合函数 的形式,需左右同乘 ,方可利用函数
的性质求解,属中档题.
13.
【分析】
求出导函数,得切线斜率后可得切线方程.
【详解】
,∴切线斜率为 ,
切线方程为 .
故答案为: .
14.
【分析】构造函数 ,对其求导,根据题中条件,由导数的方法判定函数单调性,进
而可求出结果.
【详解】
构造函数 , ,
因为对任意 ,都有 ,
所以 恒成立,
所以函数 在R上单调递增,
由 ,解得 ,
所以 的取值范围为 .
故答案为: .
【点睛】
关键点点睛:
求解本题的关键在于,构造函数 ,结合题中条件,由导数的方法判定函数
单调性,即可求解出结果.
15. .【分析】
求导数,确定极小值,由极小值为0求得 .
【详解】
由题意 ,
∵ ,∴ 或 时, , 时, ,
∴ 在 和 上递增,在 上递减,
的极小值是 ,解得 ( 舍去).
故答案为:
16.
【分析】
“若 ,使得 ”转换为集合交集非空,分别根据导数求 ,
的值域,进一步求出答案.
【详解】
因为
所以当 , ,所以 单调递减,
因为 ,所以 ,
当 , ,所以 单调递增,
因为 ,使得 ,
所以
所以 .
故答案为: .
【点睛】
本题考查的是导数综合的问题,涉及到函数单调性以及恒成立的问题,属中档题.
本题主要是转换的思想,“若 ,使得 ”可以转换为集合交集
非空.
17.(1) ;(2)函数 的单调增区间为 , ;减区间
为 ;极大值 ,极小值 .【分析】
(1)求出 和 的值,利用点斜式可得出所求切线的方程;
(2)求出函数 的极值点,列表分析函数 的单调性以及导数符号的变
化,即可得出函数 的单调区间和极值.
【详解】
解:(1)因为 ,所以
当 时, , ,
所以曲线 在点 处的切线过点 ,斜率为
所以切线方程为 ,即 .
(2)函数 的定义域为
令 得,
增 极大值 减 极小值 增
所以函数 的单调增区间为 , ;减区间为当 时,函数 有极大值,
当 时,函数 有极小值, .
【点睛】
本题考查利用导数求函数的切线方程,同时也考查了利用导数求函数的单调区间和极值,
考查计算能力,属于基础题.
18.(1) 在 上为减函数;(2) , .
【分析】
(1)利用导数判断函数的单调性即可.
(2)根据函数的单调性即可得到函数的最值.
【详解】
(1) , ,
, , 在 上为减函数.
(2)由(1)知 在 上为减函数,
, .
19.(1) ;(2) .
【分析】(1)代入已知点的坐标可得 的解析式;
(2)设切点为为 ,然后利用导数的几何意义求解.
【详解】
(1)由题意 , ,∴ ;
(2)由(1) ,设切点为 ,
,∴ ,又 ,两者结合可解得 , .
【点睛】
方法点睛:本题导数的几何意义.求函数 的切线方程的方法:
(1)若求函数 的图象在 处的切线,则只要求得 ,由 是切线斜
率可得切线方程;
(2)若求过 的切线方程,则一般设切点为 ,由(1)求出在 点的切
线方程 ,由切线过点 求出切点坐标,得切线方程.已知切
线方程也是同样求解.
20.(1) , , ;(2)极小值为0,极大值为 .
【分析】
(1)由导数的几何意义可得 ,再由点 在切线上即可得解;
(2)利用导数确定函数的单调性,结合极值的概念即可得解.【详解】
(1)因为 ,切线 的斜率为 ,
所以 ,
又 ,所以 ,
所以 ,由点 在直线 上,可得 ,
即 ,
所以 ;
(2)由(1)得 ,则 ,
当 时, ;当 时, ;
所以 的单调增区间为 ,减区间为 ,
所以函数 的极小值为 ,极大值为 .
21.(1) 在 和 上递增,在 上递减;(2)
【分析】
(1)代入 的值,求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)求出函数的导数,结合二次函数的性质得到关于 的不等式组,解出即可【详解】
解:(1)当 时, ,则 ,
令 ,得 或 ,令 ,得 ,
所以 在 和 上递增,在 上递减;
(2) ,令 ,
若函数 在 上单调递减,则 在 上恒成立,
则 ,解得 ,
所以a的取值范围为 ,
【点睛】
此题考查导数的应用,考查利用导数求函数的单调区间,考查由函数的单调性求参数范围,
考查二次函数的性质,属于基础题
22.(1)当 时, 没有极值;当 时,
, ;当 时, ,
.(2) .
【分析】(1)首先求出 的解析式,再求出导函数 ,再对参数 分类
讨论,求出函数的单调区间与极值;
(2)设 ( )求出函数的导函数,依题意 在 时
恒成立即可,从而求出参数的取值范围;
【详解】
解:(1) , 的定义域为
,
① ,即 时, 在 和 上递增,在 上递减,
, ;
② ,即 时, 在 上递增, 没有极值;
③ ,即 时, 在 和 上递增, 在 上递减,
∴ , .
综上可知:当 时, 没有极值;当 时, ,
;
当 时, , .
(2)设 ( ), ,
设 ,则 , ,
,
∴ 在 上递增,∴ 的值域为 ,
①当 时, , 为 上的增函数,
∴ ,适合条件;
②当 时,∵ ,∴不适合条件;
③当 时,对于 , ,令 , ,存在 ,
使得 时, .
∴ 在 上单调递减,∴ ,
即在 时, ,∴不适合条件.
综上, 的取值范围为 .
【点睛】
导函数中常用的两种常用的转化方法:一是利用导数研究含参函数的单调性,常化为不等
式恒成立问题.注意分类讨论与数形结合思想的应用;二是函数的零点、不等式证明常转
化为函数的单调性、极(最)值问题处理.