文档内容
新蔡县第一高级中学2024-2025学年高一下学期2月份开学考试数学试题
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一
个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.
1.已知集合 , ,则 ( )
A. B. C. D.
2.已知 ,则“ ”是“ ”的( )条件
A.充要 B.充分不必要 C.必要不充分 D.既不充分也不必要
3.已知 ,则 的最小值为( )
A.4 B.5 C.6 D.7
4.已知函数 在其定义域内为偶函数,且 ,则
( )
A.0 B. C.2025 D.
5.已知函数 在 上是减函数,则a的取值范围为( )
A. B. C. D.
6.令定义在 上的非常数奇函数 的表达式为 ,且 ,则 的值为( )
A. B. C. D.4
7.若 ,则 的大小关系为( )
A. B.
C. D.8.设函数 ,则函数 零点的个数为( )
A.8 B.9 C.10 D.11
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对得6分,部分选对的得部分分,选对但不全的得部分分,有选错的得0
分.
9.2021年某地居民人均可支配收入的构成比例如图所示,已知该地居民人均经营净收入为5250元,则
( )
A.2021年该地居民人均经营净收入占居民人均可支配收入的21%
B.2021年该地居民人均可支配收入为25000元
C.2021年该地居民人均转移净收入低于人均经营净收入
D.2021年该地居民人均工资性收入比人均转移净收入多6750元
10.袋子中有4个大小质地完全相同的球,其中2个红球、2个黄球,从中不放回依次摸出2个球,记
“恰有一次摸到红球”, “两次都摸到红球”, “两次都摸到黄球”, “至少有一次摸
到红球”, “至多一次摸到红球”.则下列说法正确的是( )
A.事件A与事件B是互斥事件 B.事件B与事件C是对立事件
C.事件C与事件D是对立事件 D.事件D与事件E是互斥事件
11.对于函数 ,如果对于其定义域 中任意给定的实数 ,都有 ,并且 ,
则称函数 为“比翼函数”.则下列说法正确的是( )
A.函数 是“比翼函数”
B.若函数 在 上为“比翼函数”,则
C.若函数 在 上为“比翼函数”,当 , ,则 ,D.若函数 在 上为“比翼函数”,其函数值恒大于0,且在 上是单调递减函数,记
,若 ,则
三、填空题:本题共3小题,每小题5分,共15分.
12.若定义在 上的奇函数 在 上单调递增,且 ,则满足 的x的取值范
围是
13.设 表示不大于x的最大整数,如 , ,若正数a满足
,则 .
14.算盘是我国古代一项伟大的发明,是一类重要的计算工具.现有一把初始状态的算盘如图所示,自右
向左,分别表示个位、十位、百位、千位等,上面一粒珠子(简称上珠)代表 ,下面一粒珠子(简称下
珠)代表 ,五粒下珠表示的数的大小等于同组一粒上珠表示的数的大小.例如,个位拨动一粒上珠,十位
拨动一粒下珠至梁上,表示数字 .现将算盘的个位、十位、百位、千位分别随机拨动一粒珠子至梁上,
设事件 “表示的四位数能被 整除”, “表示的四位数能被 整除”,则
.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.已知幂函数 为偶函数.
(1)求 的值;
(2)若函数 在区间 上单调,求实数 的取值范围.
16.国务院于2023年开展第五次全国经济普查,为更好地推动第五次全国经济普查工作,某地充分利用
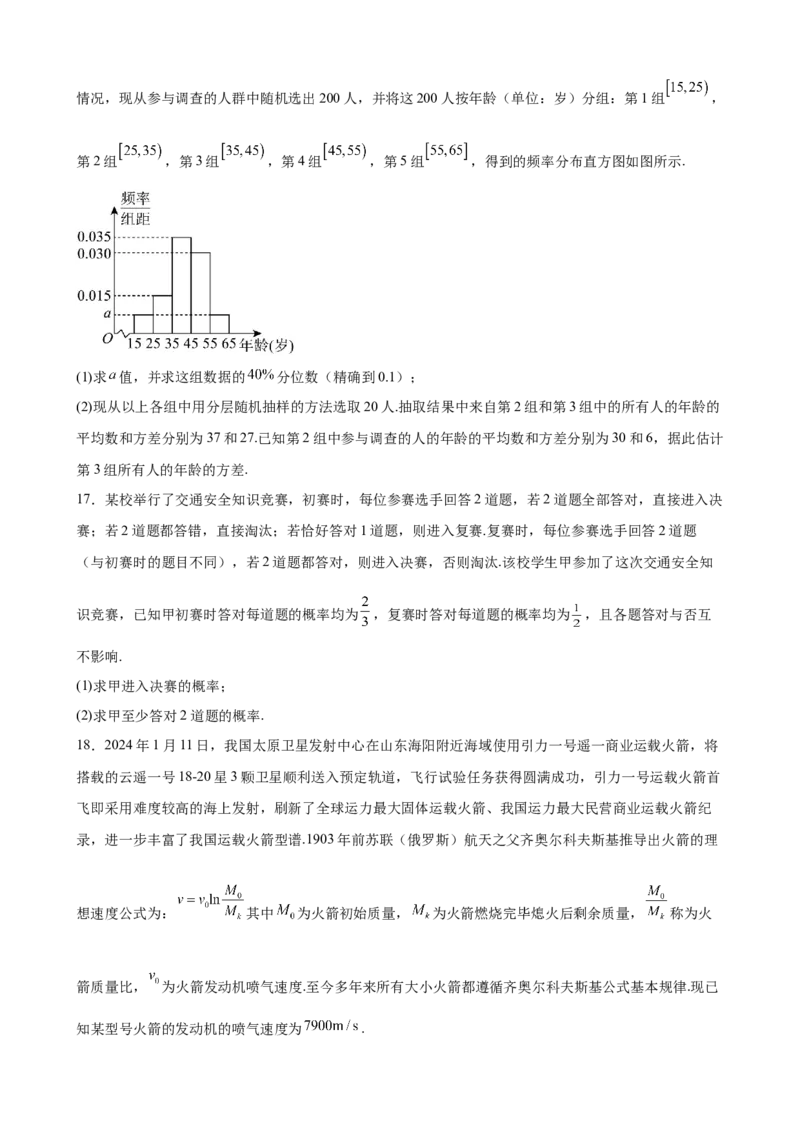
信息网络开展普查宣传,向基层普查人员,广大普查对象及社会公众宣传经济普查知识.为了解宣传进展情况,现从参与调查的人群中随机选出200人,并将这200人按年龄(单位:岁)分组:第1组 ,
第2组 ,第3组 ,第4组 ,第5组 ,得到的频率分布直方图如图所示.
(1)求 值,并求这组数据的 分位数(精确到0.1);
(2)现从以上各组中用分层随机抽样的方法选取20人.抽取结果中来自第2组和第3组中的所有人的年龄的
平均数和方差分别为37和27.已知第2组中参与调查的人的年龄的平均数和方差分别为30和6,据此估计
第3组所有人的年龄的方差.
17.某校举行了交通安全知识竞赛,初赛时,每位参赛选手回答2道题,若2道题全部答对,直接进入决
赛;若2道题都答错,直接淘汰;若恰好答对1道题,则进入复赛.复赛时,每位参赛选手回答2道题
(与初赛时的题目不同),若2道题都答对,则进入决赛,否则淘汰.该校学生甲参加了这次交通安全知
识竞赛,已知甲初赛时答对每道题的概率均为 ,复赛时答对每道题的概率均为 ,且各题答对与否互
不影响.
(1)求甲进入决赛的概率;
(2)求甲至少答对2道题的概率.
18.2024年1月11日,我国太原卫星发射中心在山东海阳附近海域使用引力一号遥一商业运载火箭,将
搭载的云遥一号18-20星3颗卫星顺利送入预定轨道,飞行试验任务获得圆满成功,引力一号运载火箭首
飞即采用难度较高的海上发射,刷新了全球运力最大固体运载火箭、我国运力最大民营商业运载火箭纪
录,进一步丰富了我国运载火箭型谱.1903年前苏联(俄罗斯)航天之父齐奥尔科夫斯基推导出火箭的理
想速度公式为: 其中 为火箭初始质量, 为火箭燃烧完毕熄火后剩余质量, 称为火
箭质量比, 为火箭发动机喷气速度.至今多年来所有大小火箭都遵循齐奥尔科夫斯基公式基本规律.现已
知某型号火箭的发动机的喷气速度为 .(1)当该型号火箭的质量比为10时,求该型号火箭的理想速度;
(2)经过改进后,该火箭发动机喷气速度变为原来2倍,火箭质量比变为原来的 ,若使火箭的理想速度
增加 ,求该火箭在技术和材料改进前的质量比. (两问结果均保留一位小数,参考数据:
)
19.意大利画家列奥纳多•达•芬奇曾经提出,固定项链的两段,使其在重力的作用下自然下垂,项链所
成的曲线是什么?这就是著名的“悬链线问题”,历史上,莱布尼兹等人曾研究并得出了悬链线的方程,
其中双曲余弦函数 尤为特殊,与此类似的还有双曲正弦函数 ( 是自
然对数的底数, ).
(1)计算 的值;
(2)类比两角差的余弦公式,写出两角差的双曲余弦公式 ______,并加以证明;
(3)判断函数 的零点个数,并求出零点.
《2025年2月21日高中数学作业》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A A B B A B B ABD AC
题号 11
答案 ACD
12. 或
13.12
14.15.1)由幂函数的定义,有 ,解得 或 ,
①当 时, ,函数 为奇函数,不合题意;
②当 时, ,函数 为偶函数,满足题意;
由上知,实数 的值为2.
(2)由(1)知, ,有 ,
又由函数 的对称轴方程为 .
若函数 在区间 上单调,有 或 .
可得 或 .故实数 的取值范围为 .
16.(1)由表中数据可得 ,解得 ,
设第40百分位数为 ,
因为前2组频率
前3组频率 ,所以 位于第三组: 内
即 .
(2)由题意得,第2组和第3组的频率分别为 ,
故第2组和第3组所抽取的人数分别为
设第2组的宣传使者的年龄平均数分为 ,方差为 ,第2组人数3人,
设第3组的宣传使者的年龄平均数为 ,方差为 ,
第3组人数7人第2组和第3组所有宣传使者的年龄平均数为 ,方差为 ,
则 ,求得 ,
即第3组所有宣传使者的年龄平均数为40,.解得 ,
即第3组所有宣传使者的年龄方差为6.
17.(1)甲初赛答对2题进入决赛的概率为 ,
甲初赛答对1题进入决赛的概率为 ,
所以甲进入决赛的概率 ;
(2)甲初赛答对2题的概率 ,
甲初赛答对1题,复赛答对2题的概率为 ,
甲初赛答对1题,复赛答对1题的概率为 ,
所以甲至少答对2道题的概率 .
18.(1)依题意, ;
(2)技术改进前的理想速度 ,
技术改进后的理想速度 ,
要使火箭的理想速率至少增加 ,
则 ,即 ,
, ,
所以 ,
所以该火箭在技术和材料改进前的质量比为19.(1)由定义可得,
所以 .
(2) ,下证明之.
事实上,
.
(3)由于
因此 ,设 ,由均值不等式,
因此
令 ,可得 或 ,而 当且仅当
可视为函数 和 的复合,由复合函数单调性, 在 上单调递增,在
上单调递减
若 即 ,则 有2解,原方程共有3个解;
令 ,设 ,方程可化为 ,解得 故另两解为
若 即 ,此时关于 的方程 仅有一解,原方程有唯一解 ;
若 即 ,此时 无解,原方程有唯一解 .
综上所述, 时,原函数有1个零点 ;时,原函数有3个零点,为 .