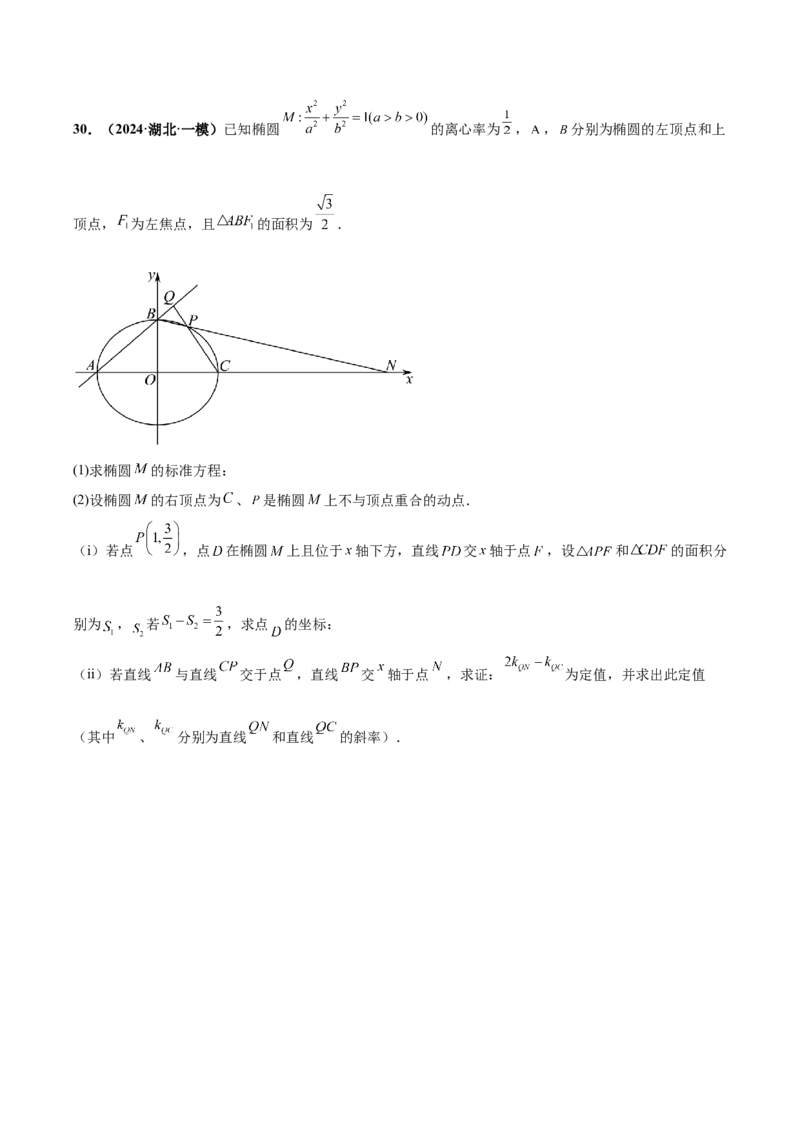文档内容
黄金冲刺大题06 圆锥曲线
(椭圆、双曲线、抛物线)(精选30题)
1.(2024·山东·二模)已知椭圆的焦点分别是 ,点 在椭圆上,且 .
(1)求椭圆的标准方程;
(2)若直线 与椭圆交于 两点,且 ,求实数 的值.
2.(2024·江苏南通·模拟预测)在平面直角坐标系 中,设椭圆 的离心率为
, , 分别是椭圆的左、右焦点,过 作两条互相垂直的直线 , ,直线 与 交于 , 两点,
直线 与 交于 , 两点,且 的周长是 .
(1)求椭圆 的方程;
(2)当 时,求 的面积.
3.(2024·河北邯郸·二模)已知椭圆 的中心为坐标原点,对称轴为 轴、 轴,且过
两点.
(1)求 的方程.
(2) 是 上两个动点, 为 的上顶点,是否存在以 为顶点, 为底边的等腰直角三角形?若存在,
求出满足条件的三角形的个数;若不存在,请说明理由.
4.(2024·广东广州·模拟预测)已知椭圆 ,右顶点为 ,上、下顶点分别为
是 的中点,且 .
(1)求椭圆 的方程;(2)设过点 的直线 交椭圆 于点 ,点 ,直线 分别交直线 于点 ,求
证:线段 的中点为定点.
5.(2024·辽宁·二模)平面直角坐标系xOy中,面积为9的正方形 的顶点 分别在x轴和y轴上
滑动,且 ,记动点P的轨迹为曲线 .
(1)求 的方程;
(2)过点 的动直线l与曲线 交于不同的两点 时,在线段 上取点Q,满足
.试探究点Q是否在某条定直线上?若是,求出定直线方程;若不是,说明理由.
6.(2024·福建厦门·三模)在直角坐标系 中,已知抛物线 的焦点为 ,过 的直
线 与 交于 两点,且当 的斜率为1时, .
(1)求 的方程;
(2)设 与 的准线交于点 ,直线 与 交于点 (异于原点),线段 的中点为 ,若 ,求
面积的取值范围.
7.(2024·浙江丽水·二模)已知抛物线 ,点 在抛物线 上,且 在 轴上方, 和 在
轴下方( 在 左侧), 关于 轴对称,直线 交 轴于点 ,延长线段 交 轴于点 ,连接
.
(1)证明: 为定值( 为坐标原点);
(2)若点 的横坐标为 ,且 ,求 的内切圆的方程.
8.(2024·江苏苏州·模拟预测)已知点 , , 和动点 满足 是 , 的等差中项.
(1)求 点的轨迹方程;
(2)设 点的轨迹为曲线 按向量 平移后得到曲线 ,曲线 上不同的两点M,N的连线交
轴于点 ,如果 ( 为坐标原点)为锐角,求实数 的取值范围;
(3)在(2)的条件下,如果 时,曲线 在点 和 处的切线的交点为 ,求证: 在一条定直线上.
9.(2024·江苏南通·二模)已知双曲线 的渐近线为 ,左顶点为 .
(1)求双曲线 的方程;
(2)直线 交 轴于点 ,过 点的直线交双曲线 于 , ,直线 , 分别交 于 , ,若 ,
, , 均在圆 上,
①求 的横坐标;
②求圆 面积的取值范围.
10.(2024·江苏南京·二模)已知抛物线 与双曲线 ( , )有公
共的焦点F,且 .过F的直线1与抛物线C交于A,B两点,与E的两条近线交于P,Q两点(均位
于y轴右侧).
(1)求E的渐近线方程;
(2)若实数 满足 ,求 的取值范围.
11.(2024·重庆·三模)已知 ,曲线 上任意一点到点 的距离是到直线 的距离的两倍.
(1)求曲线 的方程;
(2)已知曲线 的左顶点为 ,直线 过点 且与曲线 在第一、四象限分别交于 , 两点,直线 、
分别与直线 交于 , 两点, 为 的中点.
(i)证明: ;(ii)记 , , 的面积分别为 , , ,则 是否为定值?若是,求出这个定值;
若不是,请说明理由.
12.(2024·河北·二模)已知椭圆 的离心率 .
(1)若椭圆 过点 ,求椭圆 的标准方程.
(2)若直线 , 均过点 且互相垂直,直线 交椭圆 于 两点,直线 交椭圆
于 两点, 分别为弦 和 的中点,直线 与 轴交于点 ,设 .
(ⅰ)求 ;
(ⅱ)记 ,求数列 的前 项和 .
13.(2024·辽宁沈阳·二模)以坐标原点为圆心的两个同心圆半径分别为 和 , 为大圆上一动点,
大圆半径 与小圆相交于点 轴于 于 点的轨迹为 .
(1)求 点轨迹 的方程;
(2)点 ,若点 在 上,且直线 的斜率乘积为 ,线段 的中点 ,当直线 与
轴的截距为负数时,求 的余弦值.
14.(2024·广东佛山·二模)两条动直线 和 分别与抛物线 相交于不同于原
点的A,B两点,当 的垂心恰是C的焦点时, .(1)求p;
(2)若 ,弦 中点为P,点 关于直线 的对称点N在抛物线C上,求 的面积.
15.(2024·广东深圳·二模)设抛物线C: ( ),直线l: 交C于A,B两点.过
原点O作l的垂线,交直线 于点M.对任意 ,直线AM,AB,BM的斜率成等差数列.
(1)求C的方程;
(2)若直线 ,且 与C相切于点N,证明: 的面积不小于 .
16.(2024·湖南·一模)已知双曲线 的渐近线方程为 , 的半焦距为 ,
且 .
(1)求 的标准方程.
(2)若 为 上的一点,且 为圆 外一点,过 作圆 的两条切线 (斜率都存在),
与 交于另一点 与 交于另一点 ,证明:
(ⅰ) 的斜率之积为定值;
(ⅱ)存在定点 ,使得 关于点 对称.
17.(2024·湖南岳阳·三模)已知动圆 过定点 且与直线 相切,记圆心 的轨迹为曲线 .
(1)已知 、 两点的坐标分别为 、 ,直线 、 的斜率分别为 、 ,证明: ;
(2)若点 、 是轨迹 上的两个动点且 ,设线段 的中点为 ,圆 与动点
的轨迹 交于不同于 的三点 、 、 ,求证: 的重心的横坐标为定值.
18.(2024·湖北·二模)已知双曲线 的方程为 ,其中是双曲线上一点,直线 与双曲线 的另一个交点为 ,直线 与双曲线
的另一个交点为 ,双曲线 在点 处的两条切线记为 与 交于点 ,线段 的中点为 ,设
直线 的斜率分别为 .
(1)证明: ;
(2)求 的值.
19.(2024·湖北·模拟预测)已知椭圆 和 的离心率相同,设 的右
顶点为 , 的左顶点为 , ,
(1)证明: ;
(2)设直线 与 的另一个交点为P,直线 与 的另一个交点为Q,连 ,求 的最大值.
参考公式:
20.(2024·山东·二模)已知椭圆 的离心率为 ,设 的右焦点为 ,左顶点为 ,
过 的直线与 于 两点,当直线 垂直于 轴时, 的面积为 .
(1)求椭圆 的标准方程;
(2)连接 和 分别交圆 于 两点.
(ⅰ)当直线 斜率存在时,设直线 的斜率为 ,直线 的斜率为 ,求 ;
(ⅱ)设 的面积为 的面积为 ,求 的最大值.21.(2024·山东潍坊·二模)已知双曲线 : 的实轴长为 ,右焦点 到一条渐
近线的距离为1.
(1)求 的方程;
(2)过 上一点 作 的切线 , 与 的两条渐近线分别交于R,S两点, 为点 关于坐标原点的
对称点,过 作 的切线 , 与 的两条渐近线分别交于M,N两点,求四边形 的面积.
(3)过 上一点Q向 的两条渐近线作垂线,垂足分别为 , ,是否存在点Q,满足 ,
若存在,求出点Q坐标;若不存在,请说明理由.
22.(23-24高三下·湖北武汉·阶段练习)已知抛物线 ,过点 的直线与抛物线 交于 两
点,设抛物线 在点 处的切线分别为 和 ,已知 与 轴交于点 与 轴交于点 ,设 与 的交
点为 .
(1)证明:点 在定直线上;
(2)若 面积为 ,求点 的坐标;
(3)若 四点共圆,求点 的坐标.
23.(2024·福建漳州·一模)已知过点 的直线 与圆 : 相交于 , 两点,
的中点为 ,过 的中点 且平行于 的直线交 于点 ,记点 的轨迹为 .
(1)求轨迹 的方程.
(2)若 为轨迹 上的两个动点且均不在 轴上,点 满足 ( , ),其中 为
坐标原点,从下面①②③中选取两个作为条件,证明另外一个成立.
①点 在轨迹 上;②直线 与 的斜率之积为 ;③ .
注:若选择不同的组合分别解答,则按第一个解答计分.24.(2024·福建福州·模拟预测)点 是椭圆 : ( )上(左、右端点除外)的一个
动点, , 分别是 的左、右焦点.
(1)设点 到直线 : 的距离为 ,证明 为定值,并求出这个定值;
(2) 的重心与内心(内切圆的圆心)分别为 , ,已知直线 垂直于 轴.
(ⅰ)求椭圆 的离心率;
(ⅱ)若椭圆 的长轴长为6,求 被直线 分成两个部分的图形面积之比的取值范围.
25.(2024·福建三明·三模)已知平面直角坐标系 中,有真命题:函数 的图象
是双曲线,其渐近线分别为直线 和y轴.例如双曲线 的渐近线分别为x轴和y轴,可将其图象
绕原点 顺时针旋转 得到双曲线 的图象.
(1)求双曲线 的离心率;
(2)已知曲线 ,过 上一点 作切线分别交两条渐近线于 两点,试探究 面积是否为
定值,若是,则求出该定值;若不是,则说明理由;
(3)已知函数 的图象为Γ,直线 ,过 的直线与Γ在第一象限交于
两点,过 作 的垂线,垂足分别为 ,直线 交于点 ,求 面积的最小值.
26.(2024·浙江绍兴·二模)已知抛物线 : 的焦点到准线的距离为2,过点 作直
线交 于M,N两点,点 ,记直线 , 的斜率分别为 , .
(1)求 的方程;(2)求 的值;
(3)设直线 交C于另一点Q,求点B到直线 距离的最大值.
27.(2024·浙江绍兴·模拟预测)已知抛物线 : 的焦点 ,直线 过 且交C于两点 ,已
知当 时, 中点纵坐标的值为 .
(1)求 的标准方程.
(2)令 ,P为C上的一点,直线 , 分别交C于另两点A,B.证明: .
(3)过 分别作 的切线 , 与 相交于 ,同时与 相交于 ,求四边形 面积取值范围.
28.(2024·河北保定·二模)平面几何中有一定理如下:三角形任意一个顶点到其垂心(三角形三条高所
在直线的交点)的距离等于外心(外接圆圆心)到该顶点对边距离的2倍.已知 的垂心为D,外心为
E,D和E关于原点O对称, .
(1)若 ,点B在第二象限,直线 轴,求点B的坐标;
(2)若A,D,E三点共线,椭圆T: 与 内切,证明:D,E为椭圆T的两个焦点.
29.(2024·浙江杭州·模拟预测)设双曲线 ,直线 与 交于 两点.
(1)求 的取值范围;
(2)已知 上存在异于 的 两点,使得 .
(i)当 时,求 到点 的距离(用含 的代数式表示);
(ii)当 时,记原点到直线 的距离为 ,若直线 经过点 ,求 的取值范围.30.(2024·湖北·一模)已知椭圆 的离心率为 , , 分别为椭圆的左顶点和上
顶点, 为左焦点,且 的面积为 .
(1)求椭圆 的标准方程:
(2)设椭圆 的右顶点为 、 是椭圆 上不与顶点重合的动点.
(i)若点 ,点 在椭圆 上且位于 轴下方,直线 交 轴于点 ,设 和 的面积分
别为 , 若 ,求点 的坐标:
(ii)若直线 与直线 交于点 ,直线 交 轴于点 ,求证: 为定值,并求出此定值
(其中 、 分别为直线 和直线 的斜率).