2001年河北高考理科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_河北

2001 年河北高考理科数学真题及答案 第Ⅰ卷 (选择题共60分) 参考公式： 正棱锥、圆锥的侧面积公式 如果事件A、B互斥，那么 1 S  cl P（A+B）=P（A）+P（B） 锥侧 2 如果事件A、B相互独立，那么 其中c表示底面周长，l表示斜高或母线长. P（A·B）=P（A）·P（B） 棱锥、圆锥的体积公式 如果事件A在一次试验中发生的 1 V  sh 概率是P，那么n次独立重复试 锥体 3 验中恰好发生k次的概率 其中s表示底面积，h表示高. P (k)CkPk(1P)nk n n 一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题 目要求的． x  （1）函数y 3sin(  )的周期、振幅依次是 2 3 （A）4π、3 （B）4π、－3 （C）π、3 （D）π、－3 （2）若S 是数列{a}的前n项和，且S  n2,则{a }是 n n n n （A）等比数列，但不是等差数列 （B）等差数列，但不是等比数列 （C）等差数列，而且也是等比数列 （D）既非等比数列又非等差数列 （3）过点A（1，－1）、B（－1，1）且圆心在直线x+y-2=0上的圆的方程是 （A）(x3)2 (y1)2  4 （B）(x3)2 (y1)2  4 （C）(x1)2 (y1)2  4 （D）(x1)2 (y1)2  4 （4）若定义在区间（-1，0）内的函数 f(x) log (x1)满足f(x) 0,则a的取值范围是 2a 1 （A）(0, ) （B） (0, 1 ] （C）( 1 ,) （D）(0,) 2 2 2 （5）若向量a=（1，1），b=（1，－1），c=（－1，2），则c= 1 3 1 3 3 1 3 1 （A） a+ b （B） a－ b （C） a b （D）－ a b 2 2 2 2 2 2 2 2 （6）若A、B是x轴上的两点，点P的横坐标为2且|PA|=|PB|．若直线PA的方程为 x y10，则直线PB的方程是 （A）x y50 （B）2x y10 （C）2yx40 （D）2x y7 0  （7）若0 ,sincosa,sincosb,则 4 第1页 | 共11页（A）a b （B）a b （C）ab1 （D）ab  2 （8）函数y 13xx3有 （A）极小值－1，极大值1 （B）极小值－2，极大值3 （C）极小值－2，极大值2 （D）极小值－1，极大值3 （9）某赛季足球比赛的计分规则是：胜一场，得3分；平一场，得1分；负一场，得0分， 一球队打完15场，积33分，若不考虑顺序，该队胜、负、平的情况共有 （A）3种 （B）4种 （C）5种 （D）6种 （10）设坐标原点为O，抛物线y2  2x与过焦点的直线交于A、B两点，则OAOB  3 3 （A） （B）－ （C）3 （D）－3 4 4 （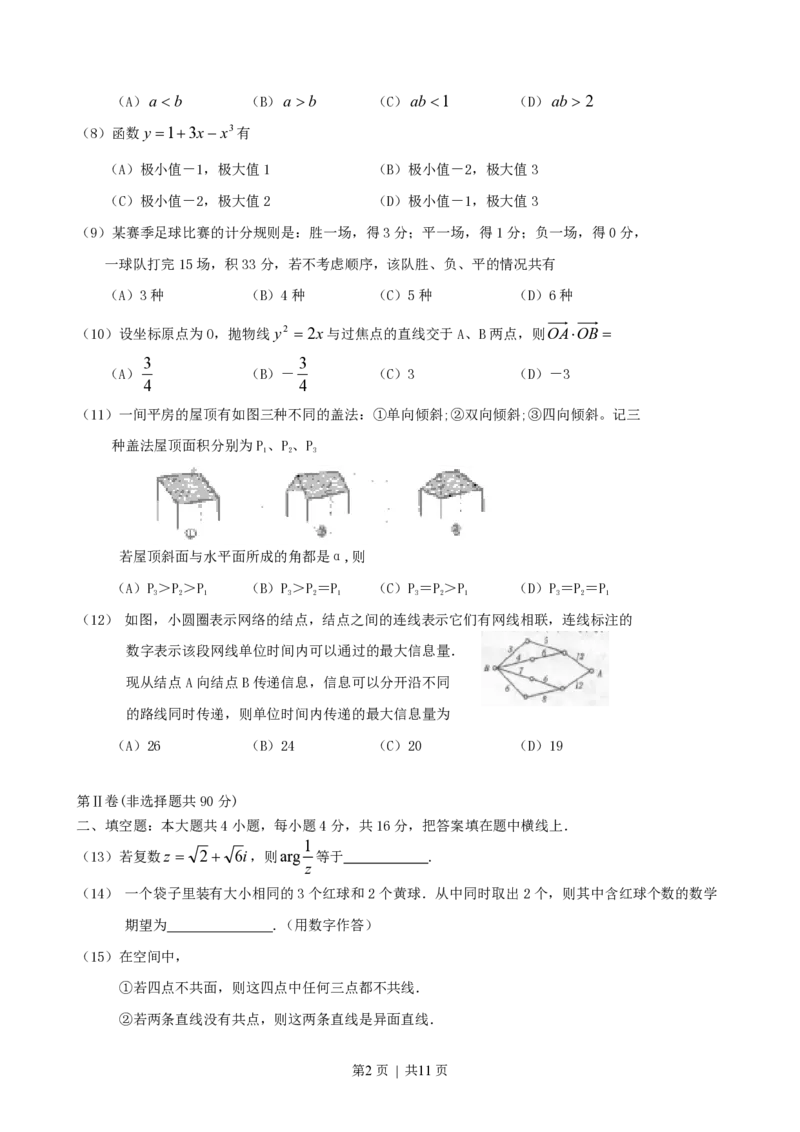11）一间平房的屋顶有如图三种不同的盖法：①单向倾斜;②双向倾斜;③四向倾斜。记三 种盖法屋顶面积分别为P、P、P 1 2 3 若屋顶斜面与水平面所成的角都是α,则 （A）P＞P＞P （B）P＞P＝P （C）P＝P＞P （D）P＝P＝P 3 2 1 3 2 1 3 2 1 3 2 1 （12） 如图，小圆圈表示网络的结点，结点之间的连线表示它们有网线相联，连线标注的 数字表示该段网线单位时间内可以通过的最大信息量． 现从结点A向结点B传递信息，信息可以分开沿不同 的路线同时传递，则单位时间内传递的最大信息量为 （A）26 （B）24 （C）20 （D）19 第Ⅱ卷(非选择题共90分) 二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上． 1 （13）若复数z  2  6i，则arg 等于 . z （14） 一个袋子里装有大小相同的3个红球和2个黄球．从中同时取出2个，则其中含红球个数的数学 期望为 .（用数字作答） （15）在空间中， ①若四点不共面，则这四点中任何三点都不共线． ②若两条直线没有共点，则这两条直线是异面直线． 第2页 | 共11页以上两个命题中，逆命题为真命题的是 ． （把符合要求的命题序号都填上） （15）设｛a｝是公比为 q的等比数列，S是它的前 n项和，若｛S｝是等差数列， n n n 则 q= . 三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤． （17）（本小题满分12分） xa 解关于x的不等式 0(aR). 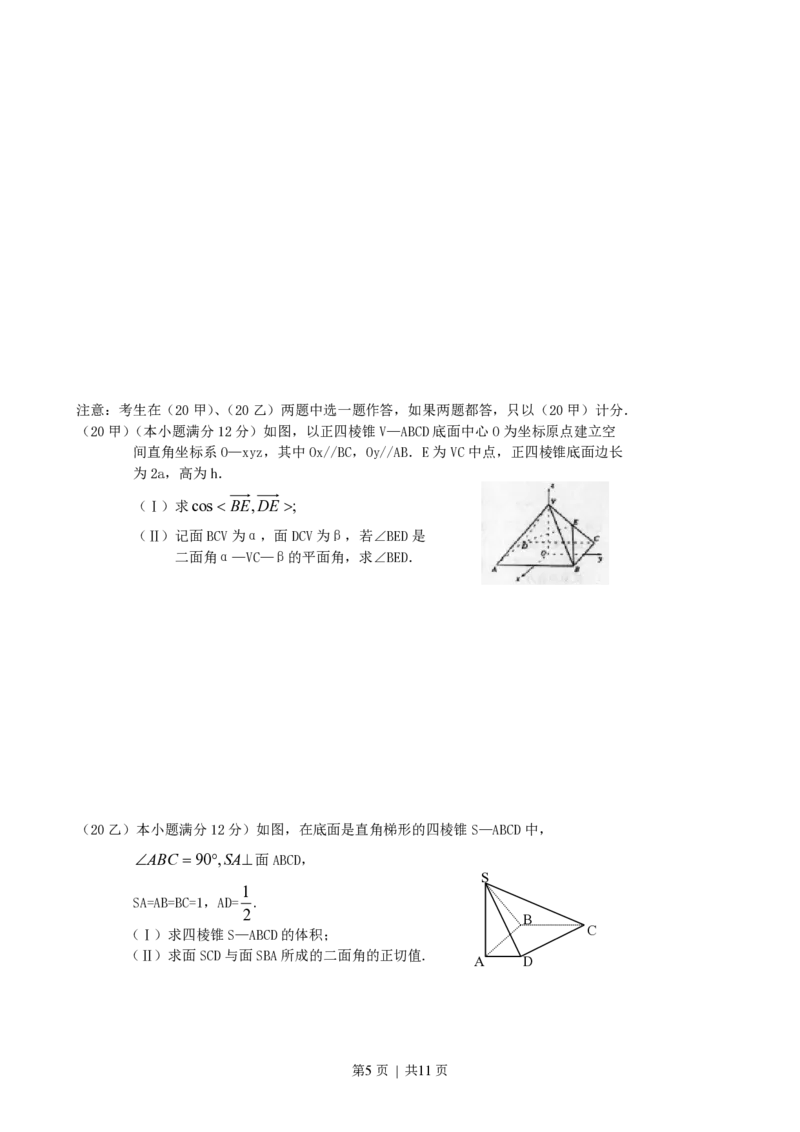xa2 （18）（本小题满分12分） 如图，用A、B、C三类不同的无件连接成两个系统N、N．当元件A、B、C都正常工作时，系统N 正 1 2 1 常工作；当元件A正常工作且元件B、C至少有一个正常工作时，系统N 正常工作．已知元件A、B、C正 2 常工作的概率依次为0.80,0.90,0.90．分别求系统N、N 正常工作的概率P、P． 1 2 1 2 — A — B — C — N 1 — B — — A — — C — N 2 第3页 | 共11页（19）（本小题满分12分） ex a 设a 0, f(x)   是R上的偶函数． a ex （Ⅰ）求a的值； （Ⅱ）证明f（x）在（0，+∞）上是增函数． 第4页 | 共11页注意：考生在（20甲）、（20乙）两题中选一题作答，如果两题都答，只以（20甲）计分． （20甲）（本小题满分12分）如图，以正四棱锥V—ABCD底面中心O为坐标原点建立空 间直角坐标系O—xyz，其中Ox//BC，Oy//AB．E为VC中点，正四棱锥底面边长 为2a，高为h． （Ⅰ）求cos BE,DE ; （Ⅱ）记面BCV为α，面DCV为β，若∠BED是 二面角α—VC—β的平面角，求∠BED． （20乙）本小题满分12分）如图，在底面是直角梯形的四棱锥S—ABCD中， ABC 90,SA面ABCD， S 1 SA=AB=BC=1，AD= . 2 B （Ⅰ）求四棱锥S—ABCD的体积； C （Ⅱ）求面SCD与面SBA所成的二面角的正切值. A D 第5页 | 共11页（21）（本小题满分12分） 某电厂冷却塔的外形是如图所示双曲线的一部分绕其中轴（即双曲线的虚轴）旋转所成的曲面，其中 A、A′是双曲线的顶点，C、C′是冷却塔上口直径的两个端点，B、B′是下底直径的两个端点，已知AA′ =14m，CC′=18m，BB′=22m，塔高20m． （Ⅰ）建立坐标系并写出该双曲线方程； （Ⅱ）求冷却塔的容积（精确到10m3，塔壁厚度不计，π取3.14）． 第6页 | 共11页（22）（本小题满分14分）  设0 ,曲线x2sin y2 cos1和x2 cos y2sin1有4个不同的交点． 2 （Ⅰ）求θ的取值范围； （Ⅱ）证明这4个交点共圆，并求圆半径的取值范围． 第7页 | 共11页参 考 答 案 一、选择题：本题考查基本知识和基本运算 （1）A （2）B （3）C （4）A （5）B （6）A （7）A （8）D （9）A （10）B （11）D （12）D 二、填空题：本题考查基本知识和基本运算 5 （13） （14）1.2 （15）② （16）1 3 三、解答题 （17）本小题主要考查分式不等式的解法，考查分类讨论的数学思想． 解：原不等式的解集是下面不等式组（Ⅰ）、（Ⅱ）的解集的并集： （Ⅰ） xa 0, （Ⅱ）xa0,    xa2 0;  xa2 0; 分情况讨论 （i）当a＜0或a＞1时，有a＜a2，此时不等式组（I）的解集为{x|a xa2},不等式组（II）的解 集为空集φ； （ii）当0 a 1时，有a2＜a，此时，不等式组（I）的解集为空集φ，不等式组（II）的解集为 {x|a2  xa}; （iii）当a=0或a=1时，原不等式无解． 综上，当a＜0或a＞1时时，原不等式的解集为{x|a xa2},当0 a 1时，原不等式的解集为 {x|a2  xa};当a=0或a=1时，原不等式的解集为φ. （18）本小题考查相互独立事件同时发生或互斥事件有一个发生的概率的计算方法，考查运用概率知识解 决实际问题的能力。 解：分别记元件A、B、C正常工作为事件A、B、C，由已知条件 P（A）=0.80, P(B)=0.90, P(C)=0.90. （I）因为事件A、B、C是相互独立的，所以，系统N 正常工作的概率 1 P=P（A·B·C）=P（A）·P（B）·P（C）=0.80×0.90×0.90=0.648. 1 故系统N 正常工作的概率为0.648. 1 （II）系统N 正常工作的概率 2 P P(A)1P(BC)]P(A)[1P(B)P(C)], 2 P(B)1P(B)10.900.10,P(C)1P(C)10.900.10,  第8页 | 共11页  P 2  0 8. 0  1[  0 1. 0  0 1. 0 ]  0 8. 0  0 9. 9  0 7. 9 2 . 故系统N 正常工作的概率为0.792. 2 （19）本小题主要考查函数的奇偶性和单调性等基本性质，指数函数和不等式的基本性质和运算，以及综 合分析问题的能力. （I） 解：依题意，对一切xR有 f(x) f(x)，即ex  a  1 aex, a ex aex 所以 1 1 对一切xR成立. (a )(ex  )0 a ex 1 由此得到a 0,即a2=1. 又因为a＞0，所以a=1. a （II）证明一：设0＜x＜x， 1 21 1 1 f(x ) f(x )ex1 ex2   (ex2 ex1)( 1) 1 2 ex1 ex2 ex1x2 1ex 2 x 1 ex 1(ex 2 x 1 1) , ex 2 x 1 由x 0,x 0,x x 0,得x x 0, ex2x1 10,1ex2x1 0. 1 2 2 1 1 2 f(x ) f(x )0,即f（x）在（0，+∞）上是增函数． 1 2 证明二：由 f(x)ex ex得 f(x)ex ex ex(e2x 1). 当x(0,)时，有ex 0,e2x 10,此时 f(x)0. 所以f（x）在（0，+∞）上是增函数． 注意：考生在（20甲）、（20乙）两题中选一题作答，如果两题都答，只以（20甲）计分． （20甲）本小题主要考查空间直角坐标的概念、空间点和向量的坐标表示以及两个向量夹角的计算方法； 考查运用向量研究空间图形的数学思想方法． 解：（I）由题意知B（a，a，0），C（―a，a，0），D（―a，―a，0），E a a h ( , , ), 2 2 2 由此得 3a a h a 3a h BE ( , , ),DE ( , , ), 2 2 2 2 2 2 3a a a 3a h h 3a2 h2 BEDE(  )(  )    , 2 2 2 2 2 2 2 4 |BE||DE| ( 3a )2 ( a )2 ( h )2  1 10a2 h2. 2 2 2 2 由向量的数量积公式有 3a2 h2   BEDE 2 4 6a2 h2 cosBE,DE   . |BE||DE| 1 10a\2h2  1 10a2 h2 10a2 h2 2 2 （II）若∠BED是二面角α—VC—β的平面角，则BECV ，即有 第9页 | 共11页 B E  C V =0． 又由C（－a，a，0），V（0，0，h），有CV (a,a,h)且 3a a h BE( , , ), 2 2 2 3a2 a2 h2 即h  2a,这时有 BECV    0, 2 2 2 6a2h2 6a2( 2a)2 1 cosBE,DE    . 10a2h2 10a2( 2a)2 3 1 1 BED BE,DE arccos( )arccos . 3 3 （20乙）本小题主要考查线面关系和棱锥体积计算，以及空间想象能力和逻辑推理能力．满分12分． 解：(Ⅰ)直角梯形ABCD的面积是 M =1 10.5 3 S 底面 (BCAD)AB 1 , 2 2 4 B C A D E∴四棱锥S—ABCD的体积是 V=1 SAM 3 底面 1 3  1 3 4 1 = . 4 （Ⅱ）延长BA、CD相交于点E，连结SE，则SE是所求二面角的棱． ∵AD∥BC, BC=2AD, ∴EA=AB=SA, ∴SE⊥SB， ∴ SA⊥面ABCD，得面SEB⊥面EBC，EB是交线，又BC⊥EB，∴BC⊥面SEB，故SE是CS在 面SEB上的射影，∴ CS⊥SE，所以∠BSC是所求二面角的平面角. ∵SB SA2  AB2  2,BC 1,BCSB, tanBSC BC  2 . SB 2 即所求二面角的正切值为 2 . 2 （21）本小题考查选择适当的坐标系建立曲线方程和解方程组等基础知识，考查应用所学积分知识、思想 和方法解决实际问题的能力. 解：（I）如图建立直角坐标系xOy，AA′在x轴上，AA′的中点为坐标原点O，CC′与BB′平行于x轴. x2 y2 1 设双曲线方程为  1(a 0,b0),则a  AA7. a2 b2 2 又设B（11，y），C（9，y），因为点B、C在双曲线上，所以有 1 2 112 y2  1 1, ① 72 b2 92 y2  2 1, ② 72 b2 由题意知 y  y  20. ③ 2 1 由①、②、③得y 12,y 8,b7 2. 1 2 x2 y2 故双曲线方程为  1. 49 98 1 （II）由双曲线方程得x2  y2 49. 2 y 8 1 设冷却塔的容积为V（m3），则V  2x2dy  ( y2 49)dy y 12 2 1 1 8 ( y3 49y) ,经计算得V 4.25103(m3). 6 12 答：冷却塔的容积为4.25103(m3). （22）本小题主要考查坐标法、曲线的交点和三角函数性质等基础知识，以及逻辑推理能力和运算能 力． 第10页 | 共11页解：（I）两曲线的交点坐标（x，y）满足方程组 x2sin y2cos1, 即x2 sincos,    x2cos y2sin1, y2 cossin. 有4个不同交点等价于x2 0,且y2 0,即 sincos0,  cossin0.   又因为0 ,所以得的取值范围为（0， ). 2 4 （II）由（I）的推理知4个交点的坐标（x，y）满足方程  x2  y2 2cos(0 ), 4  即得4个交点共圆，该圆的圆心在原点，半径为r  2cos(0 ). 4   2 因为cos在(0, )上是减函数，所以由cos01,cos  . 4 4 2 知r的取值范围是(4 2, 2). 第11页 | 共11页