文档内容
2023—2024 学年第二学期高一年期末质量检测
数学学科试卷
(完卷时间:120分钟;满分:150分)
注意事项:
1.答题前、考生务必在试题卷、答题卡规定的地方填写自己的准考证号、姓名.考生要认真
核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号、姓名是否一致.
2.第I卷每小题选出答案后,用 2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其它答案标号.第Ⅱ卷用0.5毫米黑色签字笔在答题卡上书写作答.
在试题卷上作答,答案无效.
3.考试结束,考生必须将答题卡交回.
第I卷
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只
有一项是符合题目要求的.
1. 已知复数 ( 为虚数单位),则 ( )
A. B. 2 C. D. 1
2. 下列命题一定正确的是( )
A. 一条直线和一个点确定一个平面
B. 如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行
C. 垂直于同一条直线的两条直线互相平行
D. 若直线 与平面 平行,则直线 与平面 内任意一条直线都没有公共点
3. 数据 , , ,…, 的平均数为 ,方差 ,则数据 , , ,…,
的标准差为( )
A. 6 B. 7 C. 12 D. 36
4. 某同学参加知识竞赛, 位评委给出的分数为 ,则该组分数的第 百分位数为
( )
A. B. C. D.
第1页/共9页
学科网(北京)股份有限公司5. 在 中,角 , , 的对边分别为 , , ,若 , , ,则 (
)
A. B. C. 2 D. 1
6. 甲和乙两位同学准备在体育课上进行一场乒乓球比赛,假设甲对乙每局获胜的概率都为 ,比赛采取三
局两胜制(当一方获得两局胜利时,该方获胜,比赛结束),则甲获胜的概率为( )
A. 5 B. C. D.
的
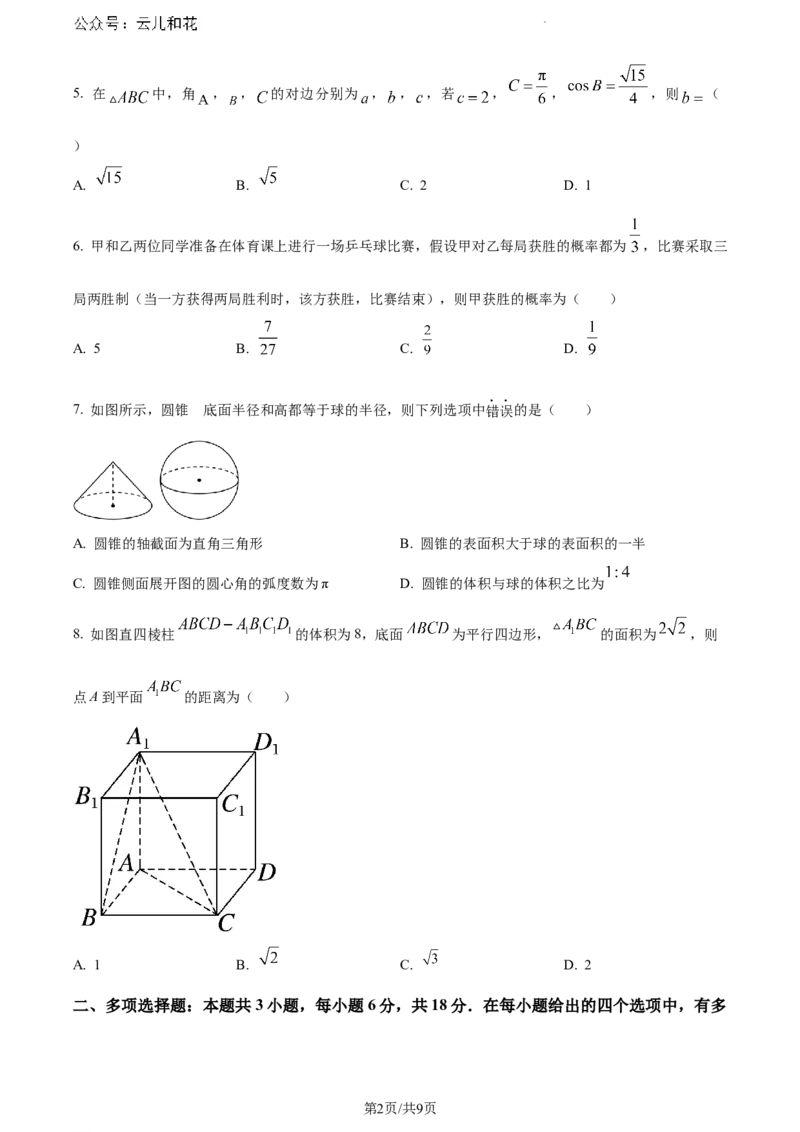
7. 如图所示,圆锥 底面半径和高都等于球的半径,则下列选项中错误的是( )
A. 圆锥的轴截面为直角三角形 B. 圆锥的表面积大于球的表面积的一半
C. 圆锥侧面展开图的圆心角的弧度数为π D. 圆锥的体积与球的体积之比为
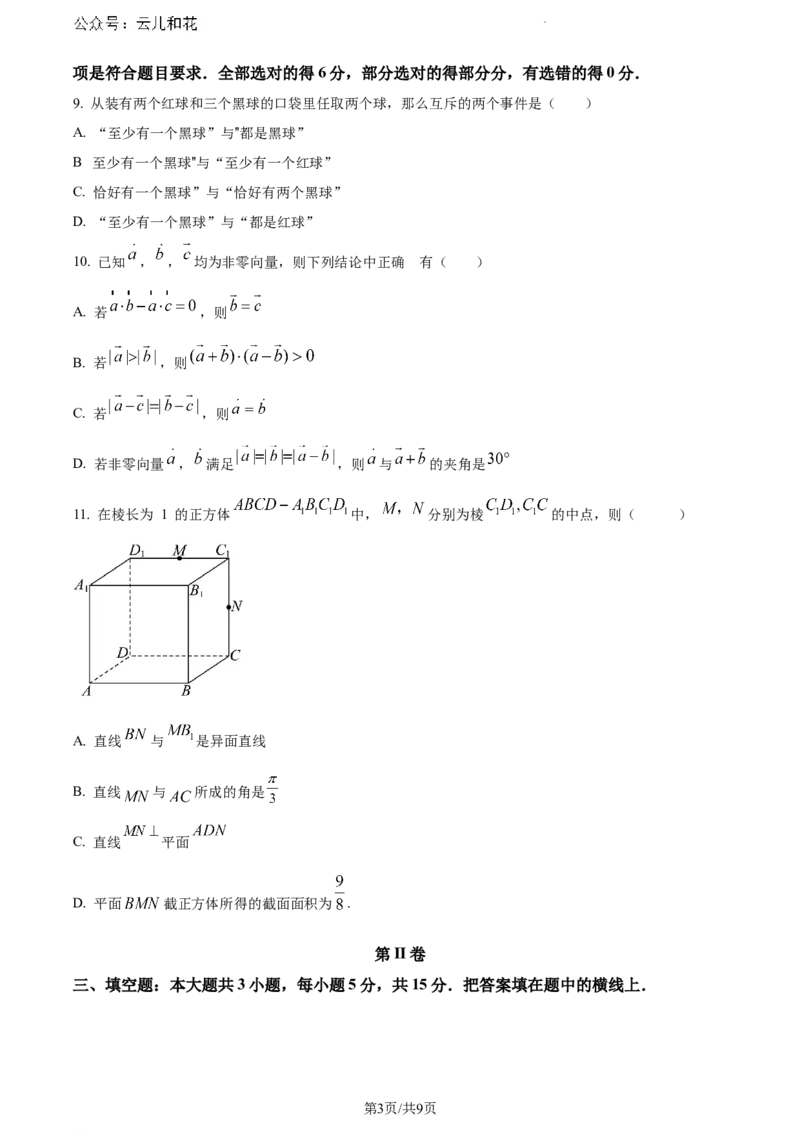
8. 如图直四棱柱 的体积为8,底面 为平行四边形, 的面积为 ,则
点A到平面 的距离为( )
A. 1 B. C. D. 2
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多
第2页/共9页
学科网(北京)股份有限公司项是符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 从装有两个红球和三个黑球的口袋里任取两个球,那么互斥的两个事件是( )
A. “至少有一个黑球”与''都是黑球”
.
B 至少有一个黑球''与“至少有一个红球”
C. 恰好有一个黑球”与“恰好有两个黑球”
D. “至少有一个黑球”与“都是红球”
的
10. 已知 , , 均为非零向量,则下列结论中正确 有( )
A. 若 ,则
B. 若 ,则
C. 若 ,则
D. 若非零向量 , 满足 ,则 与 的夹角是
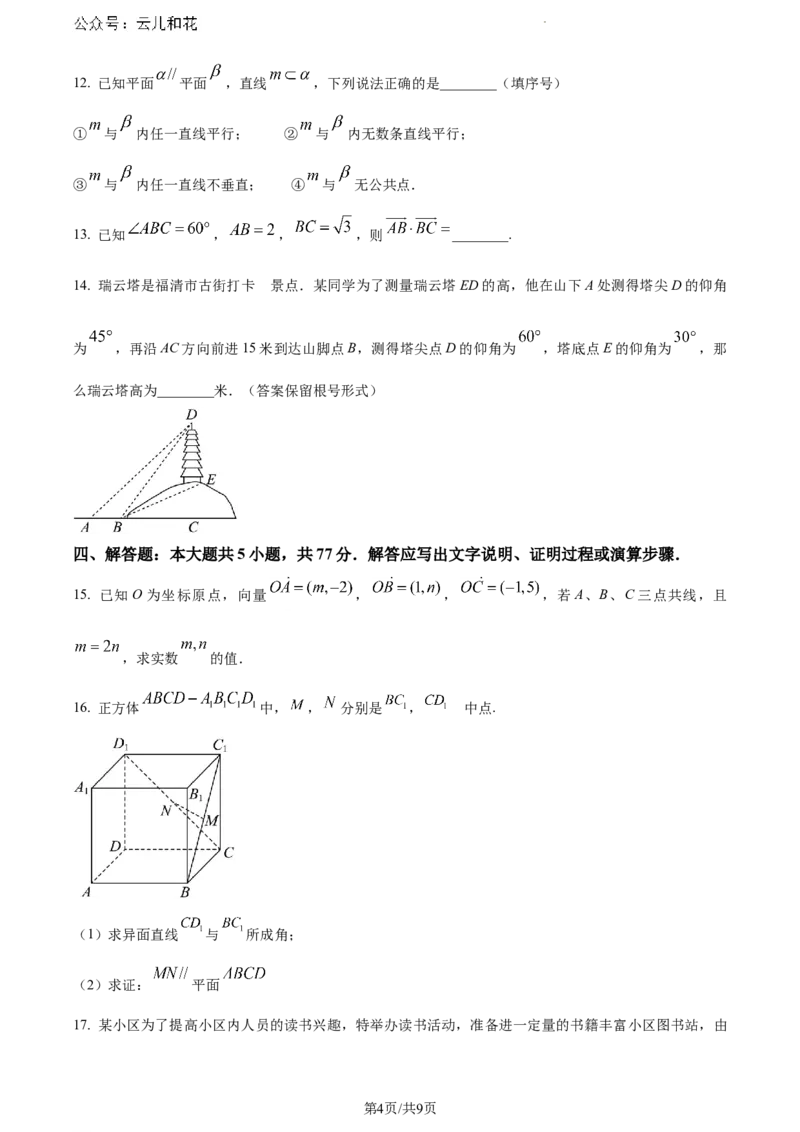
11. 在棱长为 1 的正方体 中, 分别为棱 的中点,则( )
A. 直线 与 是异面直线
B. 直线 与 所成的角是
C. 直线 平面
D. 平面 截正方体所得的截面面积为 .
第II卷
三、填空题:本大题共3小题,每小题5分,共15分.把答案填在题中的横线上.
第3页/共9页
学科网(北京)股份有限公司12. 已知平面 平面 ,直线 ,下列说法正确的是________(填序号)
① 与 内任一直线平行; ② 与 内无数条直线平行;
③ 与 内任一直线不垂直; ④ 与 无公共点.
13. 已知 , , ,则 ________.
的
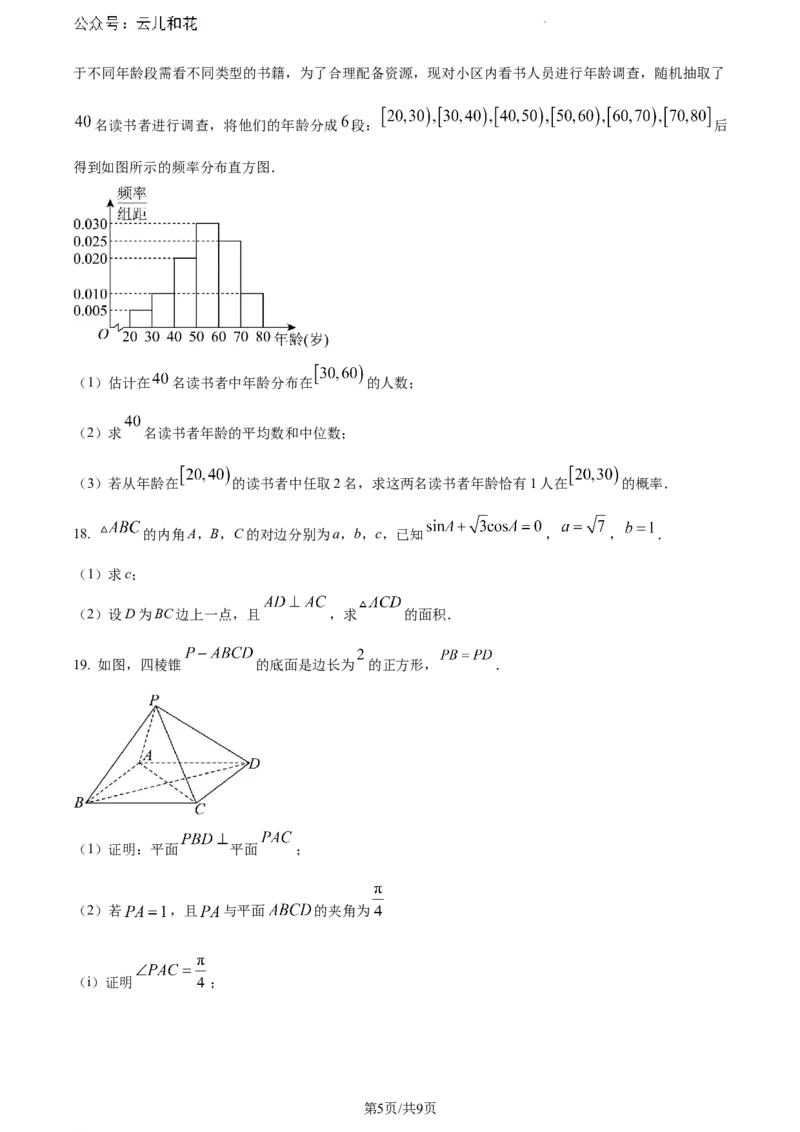
14. 瑞云塔是福清市古街打卡 景点.某同学为了测量瑞云塔ED的高,他在山下A处测得塔尖D的仰角
为 ,再沿AC方向前进15米到达山脚点B,测得塔尖点D的仰角为 ,塔底点E的仰角为 ,那
么瑞云塔高为________米.(答案保留根号形式)
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知O为坐标原点,向量 , , ,若A、B、C三点共线,且
,求实数 的值.
的
16. 正方体 中, , 分别是 , 中点.
(1)求异面直线 与 所成角;
(2)求证: 平面
17. 某小区为了提高小区内人员的读书兴趣,特举办读书活动,准备进一定量的书籍丰富小区图书站,由
第4页/共9页
学科网(北京)股份有限公司于不同年龄段需看不同类型的书籍,为了合理配备资源,现对小区内看书人员进行年龄调查,随机抽取了
名读书者进行调查,将他们的年龄分成 段: 后
得到如图所示的频率分布直方图.
(1)估计在 名读书者中年龄分布在 的人数;
(2)求 名读书者年龄的平均数和中位数;
(3)若从年龄在 的读书者中任取2名,求这两名读书者年龄恰有1人在 的概率.
18. 的内角A,B,C的对边分别为a,b,c,已知 , , .
(1)求c;
(2)设D为BC边上一点,且 ,求 的面积.
19. 如图,四棱锥 的底面是边长为 的正方形, .
(1)证明:平面 平面 ;
(2)若 ,且 与平面 的夹角为
(i)证明 ;
第5页/共9页
学科网(北京)股份有限公司(ii)求二面角 的正弦值.
第6页/共9页
学科网(北京)股份有限公司2023—2024 学年第二学期高一年期末质量检测
数学学科试卷
(完卷时间:120分钟;满分:150分)
注意事项:
1.答题前、考生务必在试题卷、答题卡规定的地方填写自己的准考证号、姓名.考生要认真
核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号、姓名是否一致.
2.第I卷每小题选出答案后,用 2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其它答案标号.第Ⅱ卷用0.5毫米黑色签字笔在答题卡上书写作答.
在试题卷上作答,答案无效.
3.考试结束,考生必须将答题卡交回.
第I卷
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只
有一项是符合题目要求的.
【1题答案】
【答案】A
【2题答案】
【答案】D
【3题答案】
【答案】A
【4题答案】
【答案】D
【5题答案】
【答案】D
【6题答案】
【答案】B
【7题答案】
【答案】C
【8题答案】
【答案】B
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多
第7页/共9页
学科网(北京)股份有限公司项是符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
【9题答案】
【答案】CD
【10题答案】
【答案】BD
【11题答案】
【答案】ABD
第II卷
三、填空题:本大题共3小题,每小题5分,共15分.把答案填在题中的横线上.
【12题答案】
【答案】②④
【13题答案】
【答案】
【14题答案】
【答案】
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
【15题答案】
【答案】 或 .
【16题答案】
【答案】(1)
(2)证明见解析
【17题答案】
【答案】(1)24 (2)平均数54,中位数为55.
(3) .
【18题答案】
【答案】(1)
第8页/共9页
学科网(北京)股份有限公司(2)
【19题答案】
【答案】(1)证明见解析
(2)(i)证明见解析;(ii)
第9页/共9页
学科网(北京)股份有限公司