文档内容
第八章 立体几何初步
(B 能力卷)
班级______ 姓名_______ 考号______
一、单项选择题(本大题共8题,每小题5分,共计40分。每小题列出的四个
选项中只有一项是最符合题目要求的)
1.已知圆锥的表面积为 ,且它的侧面展开图是一个半圆,则这个圆锥的底面直径是(
)
A.1 B.2 C.3 D.4
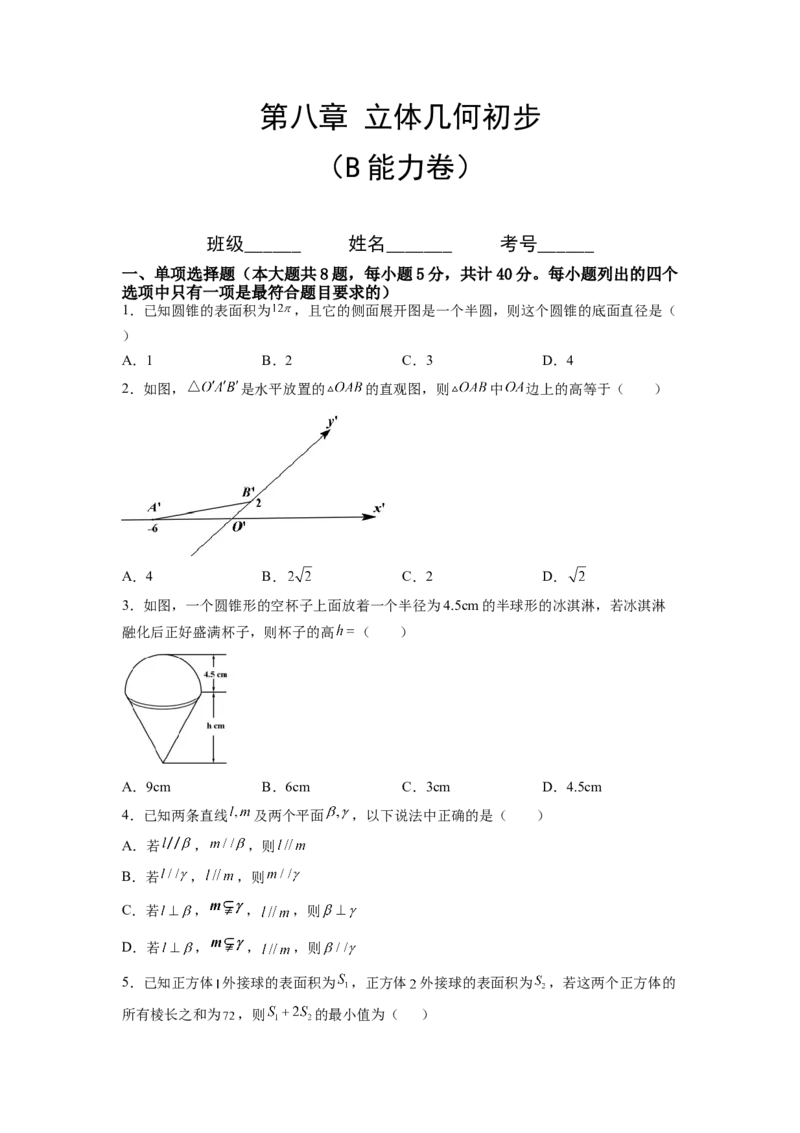
2.如图, 是水平放置的 的直观图,则 中 边上的高等于( )
A.4 B. C.2 D.
3.如图,一个圆锥形的空杯子上面放着一个半径为4.5cm的半球形的冰淇淋,若冰淇淋
融化后正好盛满杯子,则杯子的高 ( )
A.9cm B.6cm C.3cm D.4.5cm
4.已知两条直线 及两个平面 ,以下说法中正确的是( )
A.若 , ,则
B.若 , ,则
C.若 , , ,则
D.若 , , ,则
5.已知正方体 外接球的表面积为 ,正方体 外接球的表面积为 ,若这两个正方体的
所有棱长之和为 ,则 的最小值为( )A. B. C. D.
6.攒尖是我国古代建筑中屋顶的一种结构样式,多见于亭阁式建筑、园林建筑.下面以圆
形攒尖为例.如图所示的建筑屋顶可近似看作一个圆锥,其轴截面(过圆锥旋转轴的截面)
是底边边长为 ,顶角为 的等腰三角形,则该屋顶的体积约为( )
A. B. C. D.
7.如图,圆锥的底面直径 ,其侧面展开图为半圆,底面圆的弦 , 则异面直
线 与 所成角的余弦值为( )
A. B.
C. D.
8.在直三棱柱 中, ,则三棱柱
外接球体积等于( )
A. B. C. D.
二、多项选择题(本大题共4题,每小题5分,共计20分。每小题列出的四个
选项中有多项是符合题目要求的,多选或错选不得分)
9.正三棱锥底面边长为3,侧棱长为 ,则下列叙述正确的是( )
A.正三棱锥高为3 B.正三棱锥的斜高为
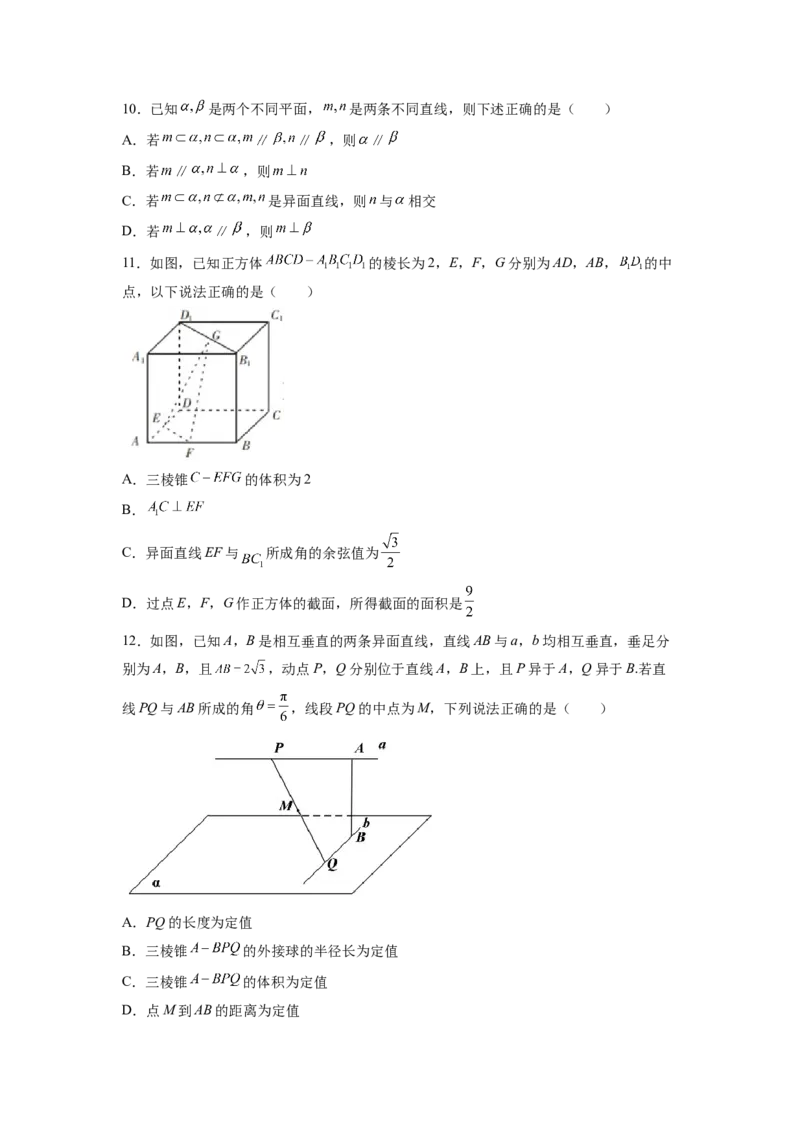
C.正三棱锥的体积为 D.正三棱锥的侧面积为10.已知 是两个不同平面, 是两条不同直线,则下述正确的是( )
A.若 ,则
B.若 ,则
C.若 是异面直线,则 与 相交
D.若 ,则
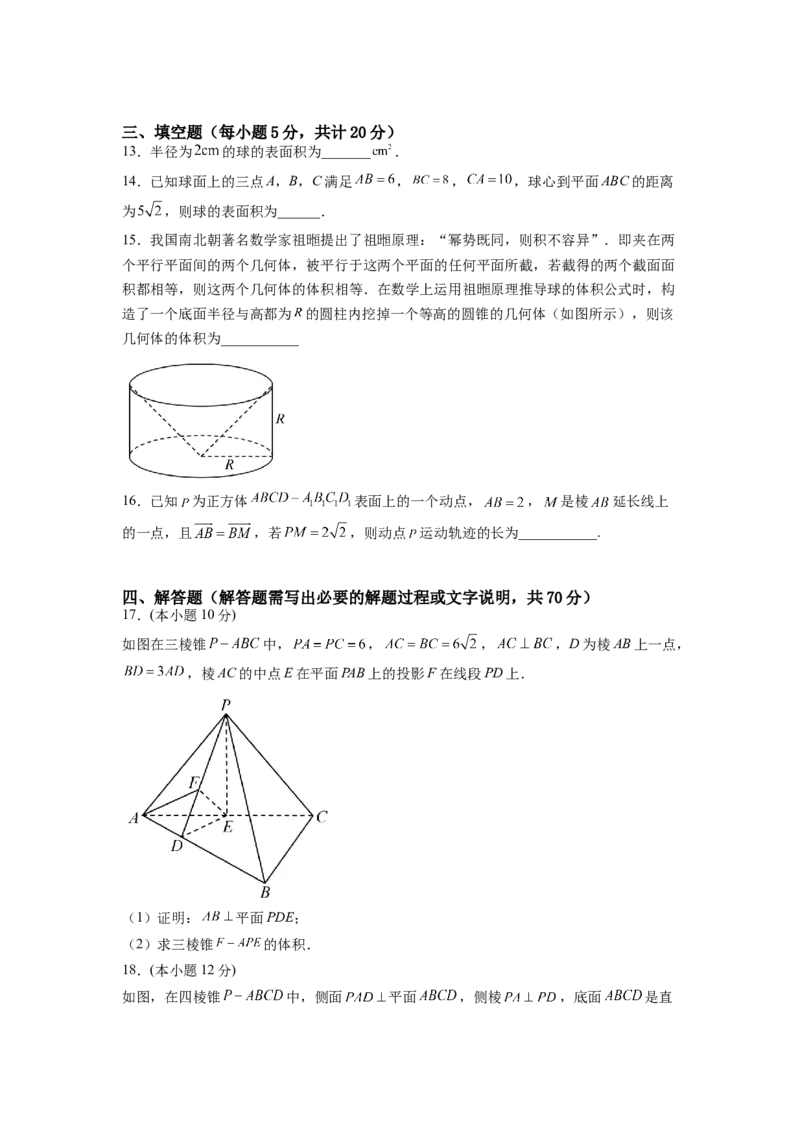
11.如图,已知正方体 的棱长为2,E,F,G分别为AD,AB, 的中
点,以下说法正确的是( )
A.三棱锥 的体积为2
B.
C.异面直线EF与 所成角的余弦值为
D.过点E,F,G作正方体的截面,所得截面的面积是
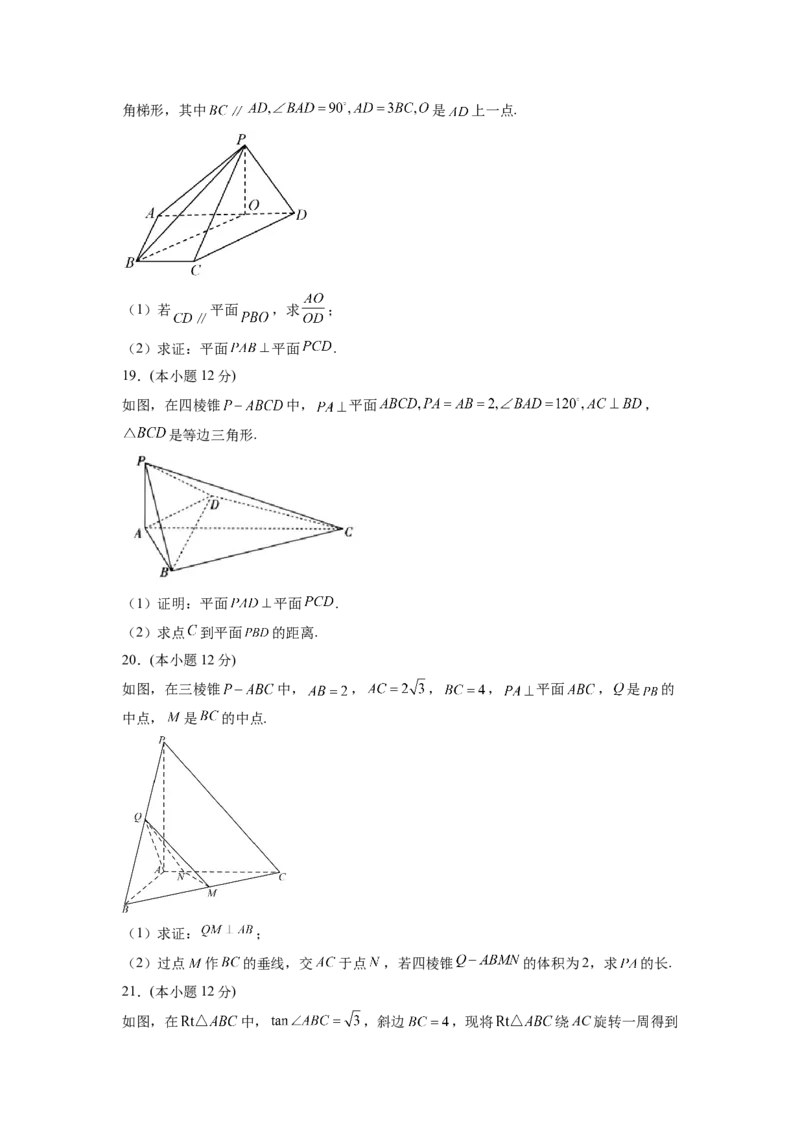
12.如图,已知A,B是相互垂直的两条异面直线,直线AB与a,b均相互垂直,垂足分
别为A,B,且 ,动点P,Q分别位于直线A,B上,且P异于A,Q异于B.若直
线PQ与AB所成的角 ,线段PQ的中点为M,下列说法正确的是( )
A.PQ的长度为定值
B.三棱锥 的外接球的半径长为定值
C.三棱锥 的体积为定值
D.点M到AB的距离为定值三、填空题(每小题5分,共计20分)
13.半径为 的球的表面积为_______ .
14.已知球面上的三点A,B,C满足 , , ,球心到平面ABC的距离
为 ,则球的表面积为______.
15.我国南北朝著名数学家祖暅提出了祖暅原理:“幂势既同,则积不容异”.即夹在两
个平行平面间的两个几何体,被平行于这两个平面的任何平面所截,若截得的两个截面面
积都相等,则这两个几何体的体积相等.在数学上运用祖暅原理推导球的体积公式时,构
造了一个底面半径与高都为 的圆柱内挖掉一个等高的圆锥的几何体(如图所示),则该
几何体的体积为___________
16.已知 为正方体 表面上的一个动点, , 是棱 延长线上
的一点,且 ,若 ,则动点 运动轨迹的长为___________.
四、解答题(解答题需写出必要的解题过程或文字说明,共70分)
17.(本小题10分)
如图在三棱锥 中, , , ,D为棱AB上一点,
,棱AC的中点E在平面PAB上的投影F在线段PD上.
(1)证明: 平面PDE;
(2)求三棱锥 的体积.
18.(本小题12分)
如图,在四棱锥 中,侧面 平面 ,侧棱 ,底面 是直角梯形,其中 是 上一点.
(1)若 平面 ,求 ;
(2)求证:平面 平面 .
19.(本小题12分)
如图,在四棱锥 中, 平面 ,
是等边三角形.
(1)证明:平面 平面 .
(2)求点 到平面 的距离.
20.(本小题12分)
如图,在三棱锥 中, , , , 平面 , 是 的
中点, 是 的中点.
(1)求证: ;
(2)过点 作 的垂线,交 于点 ,若四棱锥 的体积为2,求 的长.
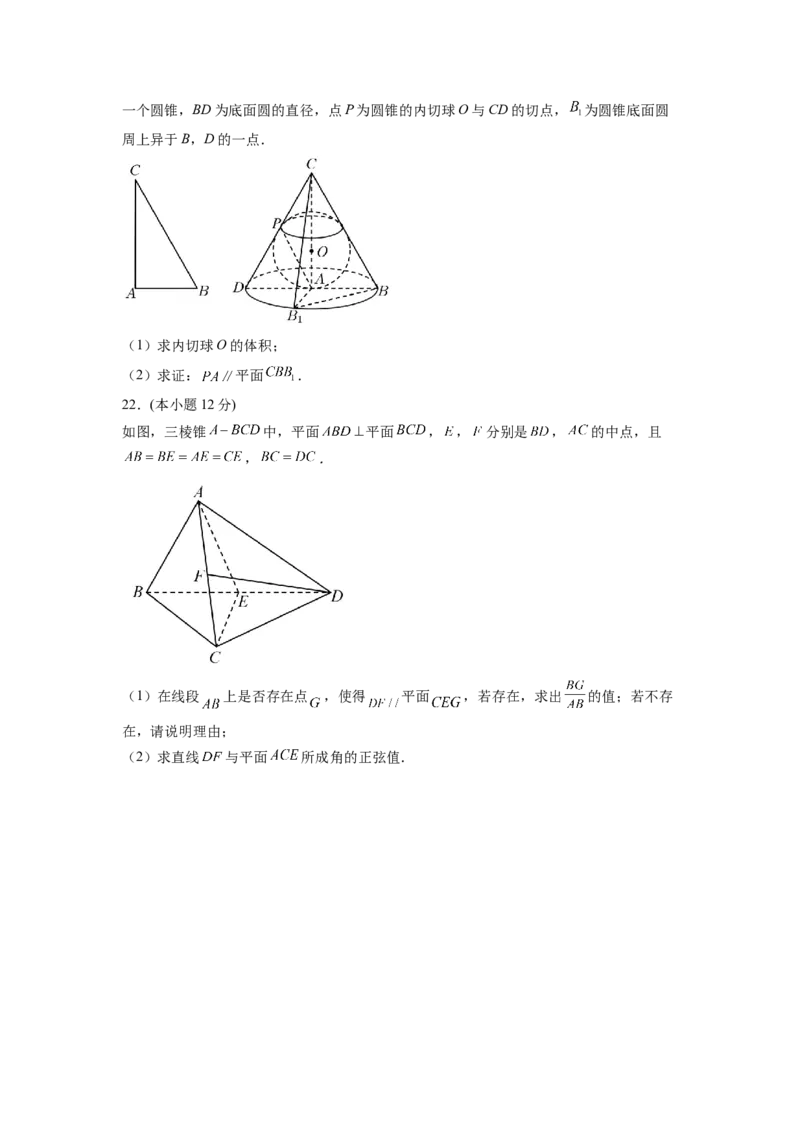
21.(本小题12分)
如图,在 中, ,斜边 ,现将 绕AC旋转一周得到一个圆锥,BD为底面圆的直径,点P为圆锥的内切球O与CD的切点, 为圆锥底面圆
周上异于B,D的一点.
(1)求内切球O的体积;
(2)求证: 平面 .
22.(本小题12分)
如图,三棱锥 中,平面 平面 , , 分别是 , 的中点,且
, .
(1)在线段 上是否存在点 ,使得 平面 ,若存在,求出 的值;若不存
在,请说明理由;
(2)求直线 与平面 所成角的正弦值.