文档内容
第四章 单元质量测评
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间
120分钟.
第Ⅰ卷(选择题,共60分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四
个选项中,只有一项是符合题目要求的)
1.函数f(x)=的定义域为( )
A. B.(2,+∞)
C.∪(2,+∞) D.∪[2,+∞)
答案 C
解析 要使函数 f(x)有意义,需使(log x)2-1>0,即(log x)2>1,∴log x>1 或
2 2 2
log x<-1.解得x>2或0且x≠1,即为∪(1,+∞).故选D.
(2x-1)
3.函数f(x)=的图象( )
A.关于原点对称 B.关于直线y=x对称
C.关于x轴对称 D.关于y轴对称
答案 D
解析 易知f(x)的定义域为R,关于原点对称.
∵f(-x)===f(x),
∴f(x)是偶函数,其图象关于y轴对称.
4.设函数f(x)=x-ln x(x>0),则y=f(x)( )
A.在区间,(1,e)内均有零点
B.在区间,(1,e)内均无零点
C.在区间内有零点,在区间(1,e)内无零点
D.在区间内无零点,在区间(1,e)内有零点
答案 D
解析 因为当x∈时,x>0,ln x<0,所以,f(x)=x-ln x>0在上恒成立,所以
f(x)在内无零点.因为f(1)f(e)==<0,所以f(x)在(1,e)内有零点.
5.已知函数f(x)是奇函数,当x>0时,f(x)=ln x,则f的值为( )
A. B.-C.-ln 2 D.ln 2
答案 C
解析 设x<0,则-x>0,于是有f(-x)=ln (-x).因为f(x)是奇函数,所以
f(-x)=-f(x)=ln (-x),所以f(x)=-ln (-x),x<0.所以f(x)=则f=f(-2)=-ln
2.
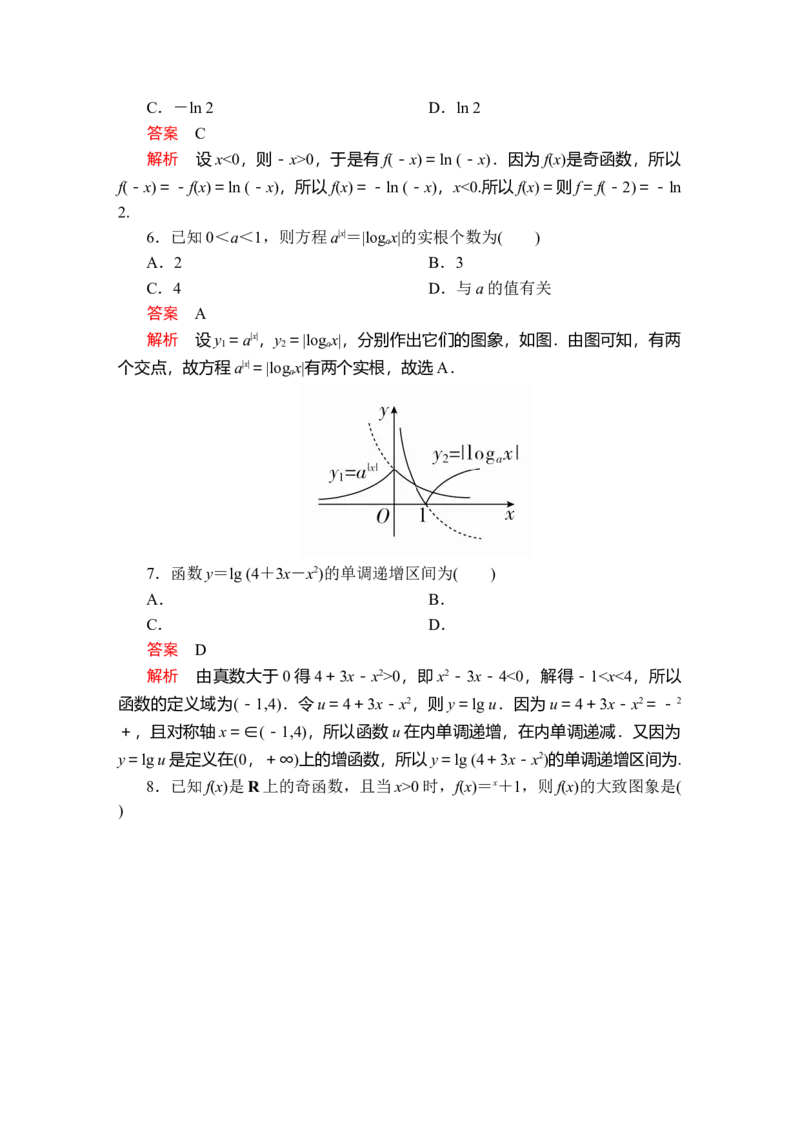
6.已知0<a<1,则方程a|x|=|log x|的实根个数为( )
a
A.2 B.3
C.4 D.与a的值有关
答案 A
解析 设y =a|x|,y =|log x|,分别作出它们的图象,如图.由图可知,有两
1 2 a
个交点,故方程a|x|=|log x|有两个实根,故选A.
a
7.函数y=lg (4+3x-x2)的单调递增区间为( )
A. B.
C. D.
答案 D
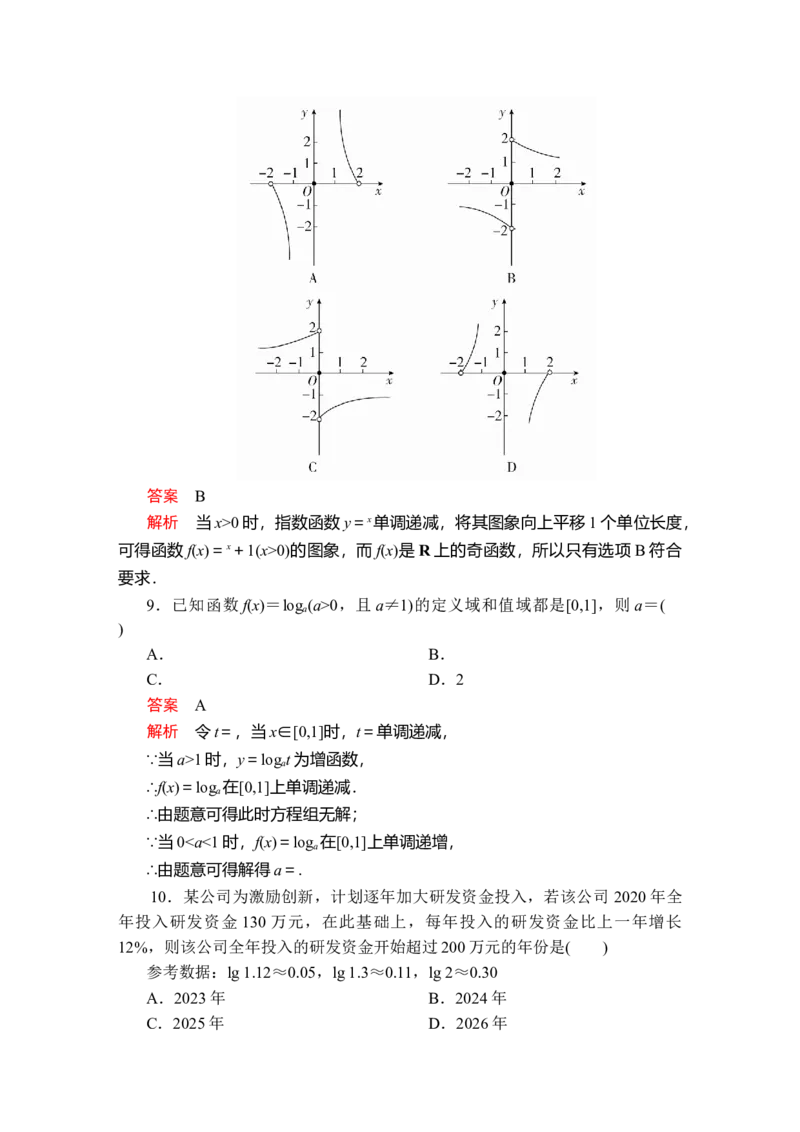
解析 由真数大于0得4+3x-x2>0,即x2-3x-4<0,解得-10时,f(x)=x+1,则f(x)的大致图象是(
)答案 B
解析 当x>0时,指数函数y=x单调递减,将其图象向上平移1个单位长度,
可得函数f(x)=x+1(x>0)的图象,而f(x)是R上的奇函数,所以只有选项 B符合
要求.
9.已知函数f(x)=log (a>0,且a≠1)的定义域和值域都是[0,1],则a=(
a
)
A. B.
C. D.2
答案 A
解析 令t=,当x∈[0,1]时,t=单调递减,
∵当a>1时,y=log t为增函数,
a
∴f(x)=log 在[0,1]上单调递减.
a
∴由题意可得此时方程组无解;
∵当0200,化简为(n-2020)lg 1.12>lg 2-lg 1.3,则n-2020>≈3.8,n≥2024.故选
B.
11.已知a=5log23.4,b=5log43.6,c=log30.3,则( )
A.a>b>c B.b>a>c
C.a>c>b D.c>a>b
答案 C
解析 ∵log 3.4>log 2=1,log 3.6b;c=
2 2 4 4
>1>b,而log 3.4>log >log ,∴a>c,故a>c>B.故
2 2 3
选C.
12.若f(x)=是R上的单调递增函数,则实数a的取值范围为( )
A.(1,+∞) B.(4,8)
C.[4,8) D.(1,8)
答案 C
解析 ∵函数f(x)是R上的单调递增函数,
∴解得4≤a<8.
故实数a的取值范围为[4,8).
第Ⅱ卷(非选择题,共90分)
二、填空题(本大题共4小题,每小题5分,共20分.将答案填在题中的横
线上)
13.用二分法求方程 x3-2x-5=0在区间(2,4)上的实数根时,取中点 x =
1
3,则下一个有根区间是________.
答案 (2,3)
解析 设f(x)=x3-2x-5,则f(2)<0,f(3)>0,f(4)>0,有f(2)f(3)<0,则
下一个有根区间是(2,3).
14.已知125x=12.5y=1000,则=________.
答案
解析 因为125x=12.5y=1000,所以x=log 1000,y=log 1000,
125 12.5
=-=log 125-log 12.5=log =log 10=.
1000 1000 1000 1000
15.细菌繁殖时,细菌数随时间成倍增长.若实验开始时有 300个细菌,以
后的细菌数如下表所示.据此表可推测实验开始前2 h的细菌数为________个.
答案 75
解析 由表中数据观察可得细菌数 y 与时间 x 的函数关系式为 y=
300×2x(x∈Z).当x=-2时,y=300×2-2==75.
16.给出函数f(x)=则f(log 3)=________.
2
答案
解析 ∵log 3<2,∴f(log 3)=f(log 3+1)=f(log 3+1+1)=f(log 3+1+1+1)
2 2 2 2 2
=f(log 24).
2
∵log 24>4,∴f(log 24)=log224=.
2 2
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或
演算步骤)
17.(本小题满分10分)计算下列各式的值:
(1)-0+-0.5+ ;
(2)lg 500+lg -lg 64+50(lg 2+lg 5)2.
解 (1)原式=+1-1++e-=+e.
(2)原式=lg 5+lg 102+lg 23-lg 5-lg 26+50(lg 10)2=lg 5+2+3lg 2-lg 5-
3lg 2+50=52.
18.(本小题满分12分)已知f(x)=(logx)2-2logx+4,x∈[2,4].
(1)设t=logx,x∈[2,4],求t的最大值与最小值;
(2)求f(x)的值域.
解 (1)因为函数t=logx在[2,4]上单调递减,所以t =log2=-1,t =log4
max min
=-2.
(2)令t=logx,则g(t)=t2-2t+4=(t-1)2+3,由(1)得t∈[-2,-1],因此
当t=-2,即x=4时,f(x) =12;当t=-1,即x=2时,f(x) =7.
max min
因此,函数f(x)的值域为[7,12].
19.(本小题满分 12分)已知f(x)是定义在 R上的奇函数,且 x>0时,f(x)=
logx.
(1)求x<0时,函数f(x)的解析式;
(2)若f(x)≤1,求实数x的取值范围.
解 (1)设x<0,则-x>0,从而f(-x)=log (-x).
∵f(x)是奇函数,∴f(x)=-f(-x)=-log (-x).
即x<0时,f(x)的解析式为f(x)=-log (-x).
当x>0时,由f(x)≤1得logx≤1,解得x≥;
当x=0时,f(x)≤1显然成立;
当x<0时,由f(x)≤1得-log (-x)≤1,
解得-2≤x<0.
综上可知,x的取值范围为-2≤x≤0或x≥.
20.(本小题满分12分)某地下车库在排气扇发生故障的情况下,测得空气中
一氧化碳含量达到了危险状态,经抢修,排气扇恢复正常.排气 4 min后,测得
车库内的一氧化碳浓度为64 ppm,继续排气4 min,又测得浓度为32 ppm,经检
测知该地下车库一氧化碳浓度 y(ppm)与排气时间 t(min)存在函数关系:y=
cmt(c,m为常数).
(1)求c,m的值;
(2)若空气中一氧化碳浓度不高于0.5 ppm为正常,问至少排气多少分钟,这
个地下车库中的一氧化碳含量才能达到正常状态?
解 (1)由题意,可得方程组
解得
所以至少排气32 min,这个地下车库中的一氧化碳含量才能达到正常状态.
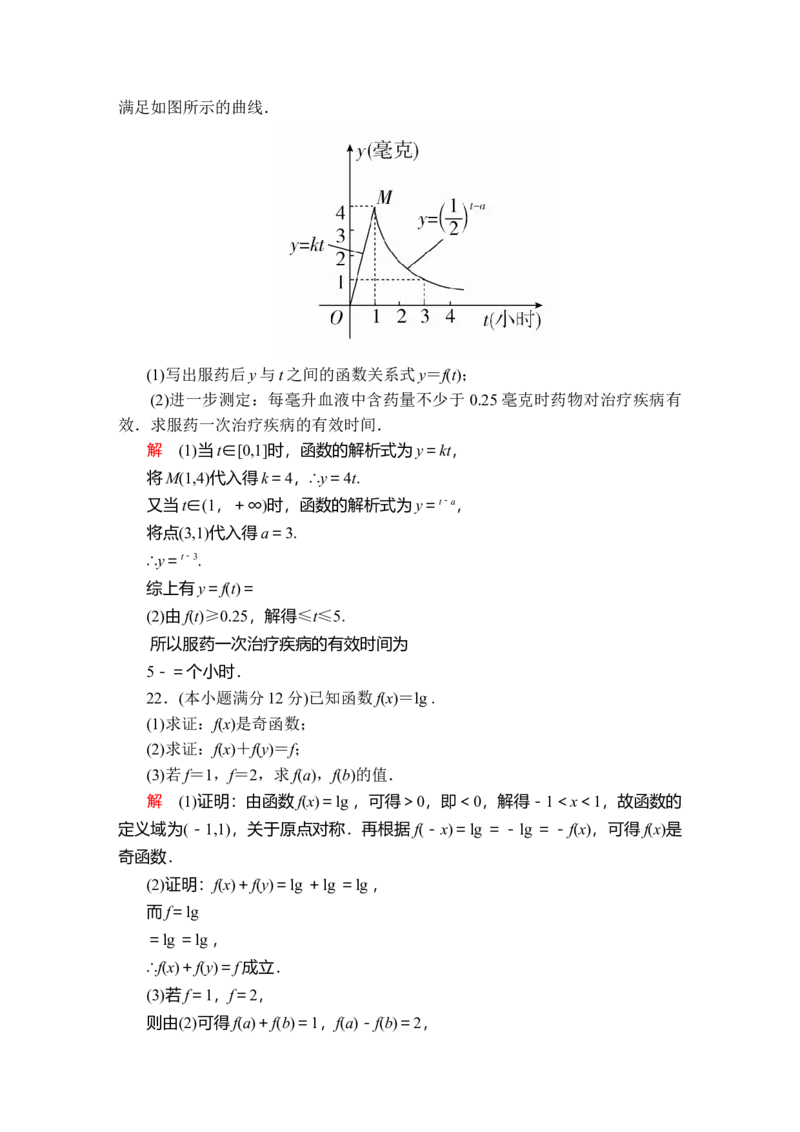
21.(本小题满分12分)某医药研究所开发一种新药,如果成年人按规定的剂
量服用,据监测,服药后每毫升血液中的含药量 y(毫克)与时间t(小时)之间近似满足如图所示的曲线.
(1)写出服药后y与t之间的函数关系式y=f(t);
(2)进一步测定:每毫升血液中含药量不少于 0.25毫克时药物对治疗疾病有
效.求服药一次治疗疾病的有效时间.
解 (1)当t∈[0,1]时,函数的解析式为y=kt,
将M(1,4)代入得k=4,∴y=4t.
又当t∈(1,+∞)时,函数的解析式为y=t-a,
将点(3,1)代入得a=3.
∴y=t-3.
综上有y=f(t)=
(2)由f(t)≥0.25,解得≤t≤5.
所以服药一次治疗疾病的有效时间为
5-=个小时.
22.(本小题满分12分)已知函数f(x)=lg .
(1)求证:f(x)是奇函数;
(2)求证:f(x)+f(y)=f;
(3)若f=1,f=2,求f(a),f(b)的值.
解 (1)证明:由函数f(x)=lg ,可得>0,即<0,解得-1<x<1,故函数的
定义域为(-1,1),关于原点对称.再根据f(-x)=lg =-lg =-f(x),可得f(x)是
奇函数.
(2)证明:f(x)+f(y)=lg +lg =lg ,
而f=lg
=lg =lg ,
∴f(x)+f(y)=f成立.
(3)若f=1,f=2,
则由(2)可得f(a)+f(b)=1,f(a)-f(b)=2,解得f(a)=,f(b)=-.