文档内容
2024 年春高一(下)期末联合检测试卷
数 学
数学测试卷共4页,满分 150分。考试时间120分钟。
注意事项:
1.答题前,考生务必将自己的准考证号、姓名、班级填写在答题卡上。考生要认真核对答题卡上粘贴的条形码
的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。
2.回答选择题时,选出每小题答案后,用 2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干
净后,再选涂其他答案标号。回答非选择题时,用 0.5 毫米的黑色墨水签字笔在答题卡上书写作答。若在试
题卷上作答,答案无效。
3.考试结束,考生必须将试题卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知复数z满足(1+i)z=2i, 则|z|=
√2
A. B. 1 C.√2 D. 2
2
2. 7.8, 7.9, 8.1, 8.1, 8.3, 8.5, 8.7, 8.9, 9.0, 9.0, 9.1, 9.1, 9.4的第60 百分位数是
A. 8.7 B. 8.9 C. 9.0 D. 9.1
3. 在△ABC中,记内角A, B, C所对的边分别为a, b, c.若 c²−ab=(a−b)²,则C=
2π
A. π/6 B. π/4 C. π/3 D.
3
4. 下列说法正确的是
A.若空间四点共面,则其中必有三点共线
B.若空间四点中任意三点不共线,则此四点共面
C.若空间四点中任意三点不共线,则此四点不共面
D.若空间四点不共面,则任意三点不共线
5. 某航空公司销售一款盲盒机票,包含哈尔滨、西安、兰州、济南、延吉 5个城市,甲乙两人计划“五一”小长假
前分别购买上述盲盒机票一张,则两人恰好到达城市相同的概率为
1 2 3 4
A. B. c. D.
5 5 5 5
高一(下)期末联合检测试卷(数学)第1页 共8页6. 记△ABC的内角A, B, C的对边分别为a, b, c,若atanB=btanA, cosA+cosB=1,则△ABC是
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
2 1
7. 在△ABC中, AB=3, AC=4, ∠BAC=60°, 且 ⃗AE= ⃗AB,⃗AF= ⃗AC,则 ⃗CE⋅⃗BF=
3 4
A. -2 B. -3 C. -4 D. -5
8. 已知正方体 ABCD−A₁B₁C₁D₁,F 为BB₁的中点,过A₁作平面α满足条件,D₁F⊥α,则α截
正方体 ABCD−A₁B₁C₁D₁所得截面为
A.六边形 B.五边形 C. 四边形 D.三角形
二、选择题:本题共 3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要
求。全部选对得6分,部分选对得部分分,有选错得0分。
9. 一个不透明袋中装有2个红球、2个白球(每个球标有不同的编号,除颜色和编号外均相同),
从中不放回依次抽取2个球,记事件A为“第一次取的球为红球”,事件 B为“第二次取的球
为白球”,则
A. P(A)=P(B) B. A, B为对立事件
5
C. A, B为相互独立事件 D.抽取的2个球中至多1个白球的概率为
6
10. 已知复数 z₁=2+3i,z₂=3−4i,z₁,z₂在复平面内对应的点分别为Z₁,Z₂,则
A.|z₁+z₂|=|z₁|+|z₂|
B.|Z Z |=5√2
1 2
C. 满足 |z|=|z₂|的复数z 对应的点 Z 形成的图形的周长是5π
D. 满足 |z₁|<|z|<|z₂|的复数z对应的点Z 形成的图形的面积是12π
11. 对棱相等的四面体被称为等腰四面体,现有一等腰四面体ABCD, AB=a, AD=b, AC=c,则下列说法
正确的是
A.该四面体各面均是全等三角形
B.该等腰四面体的面可以是直角三角形
C. 若E为AB中点, F为CD中点, 则EF⊥AB, EF⊥CD
√2
D.该四面体的体积为 √(a2+b2−c2)(b2+c2−a2)(c2+a2−b2)
12
高一(下)期末联合检测试卷(数学)第2页 共8页三、填空题:本题共3小题,每小题5分,共15分。
12.放风筝是一项有益的运动,现对高一和高二共1500名同学进行按比例分层抽样调查,统计近两年放过风
筝的人数,有如下数据:高一学生抽取有效样本 40,放过风筝的人数为19;高二学生抽取有效样本
60,放过风筝的人数为m,由此估计两个年级近两年放过风筝的人数约为540,则m= .
13. 已知复数z₁, z₂分别为方程. x²−2x+6=0的两根,则 z
1
2+2z
2
=.
¯
14. 已知a, b, c为单位向量, 且 |2a−b|=√7,则 |3a−c|+|b−c| 的最小值为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)
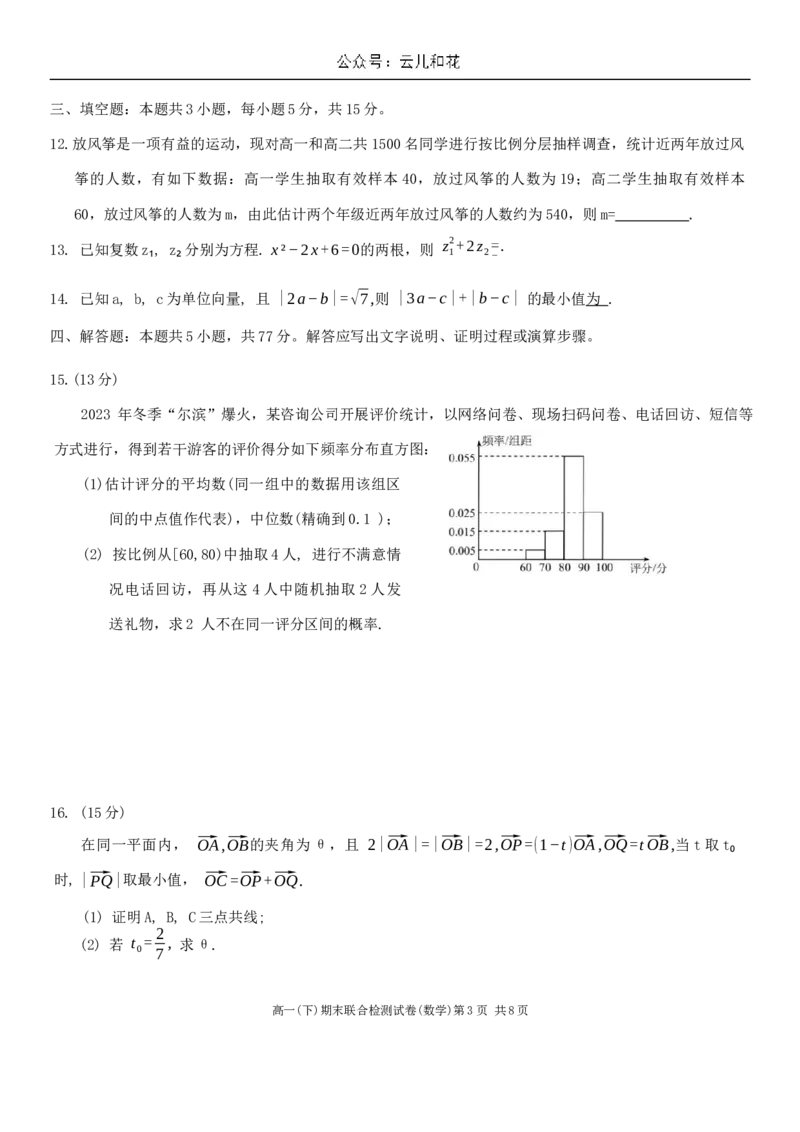
2023 年冬季“尔滨”爆火,某咨询公司开展评价统计,以网络问卷、现场扫码问卷、电话回访、短信等
方式进行,得到若干游客的评价得分如下频率分布直方图:
(1)估计评分的平均数(同一组中的数据用该组区
间的中点值作代表),中位数(精确到0.1 );
(2) 按比例从[60,80)中抽取4人, 进行不满意情
况电话回访,再从这 4人中随机抽取2人发
送礼物,求2 人不在同一评分区间的概率.
16. (15分)
在同一平面内, ⃗OA,⃗OB的夹角为θ,且 2|⃗OA|=|⃗OB|=2,⃗OP=(1−t)⃗OA,⃗OQ=t⃗OB,当t取t₀
时, |⃗PQ|取最小值, ⃗OC=⃗OP+⃗OQ.
(1) 证明A, B, C三点共线;
2
(2) 若 t = , 求θ.
0 7
高一(下)期末联合检测试卷(数学)第3页 共8页17. (15分)
π
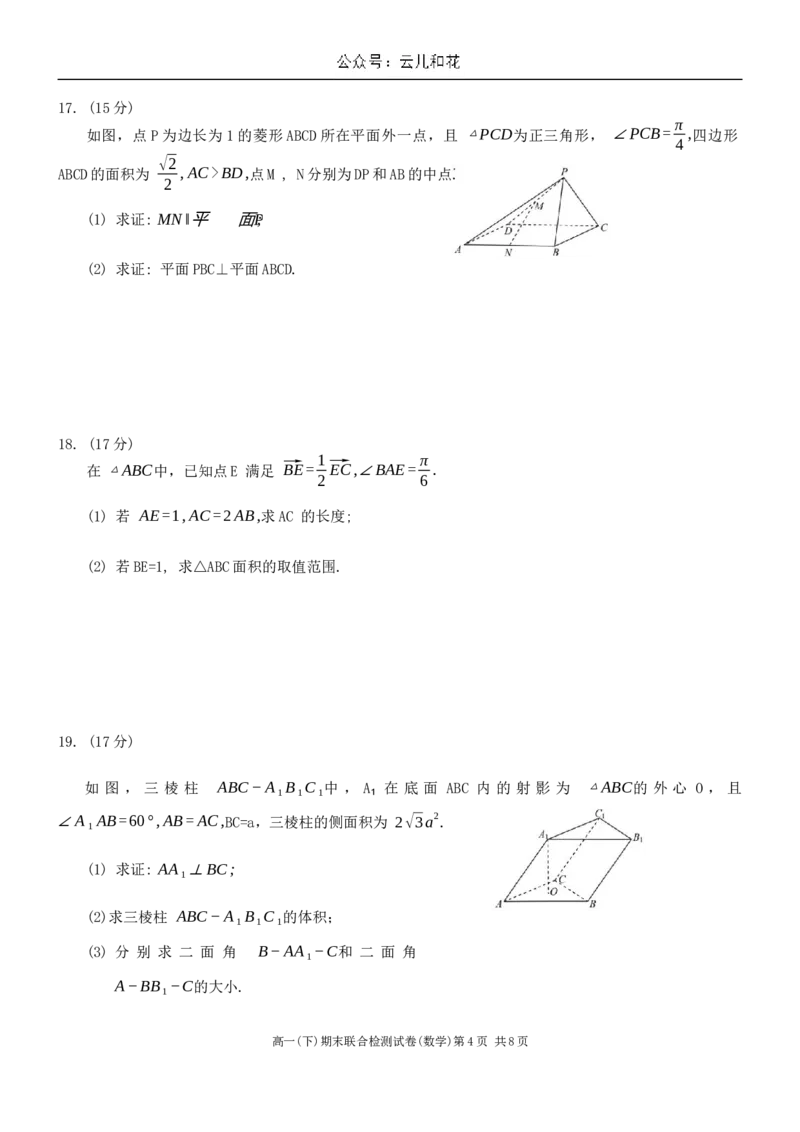
如图,点P为边长为1的菱形ABCD所在平面外一点,且 △PCD为正三角形, ∠PCB= ,四边形
4
√2
ABCD的面积为 ,AC>BD,点M , N分别为DP和AB的中点.
2
(1) 求证: MN‖平 面P;BC
(2) 求证: 平面PBC⊥平面ABCD.
18. (17分)
1 π
在 △ABC中,已知点E 满足 ⃗BE= ⃗EC,∠BAE= .
2 6
(1) 若 AE=1,AC=2AB,求AC 的长度;
(2) 若BE=1, 求△ABC面积的取值范围.
19. (17分)
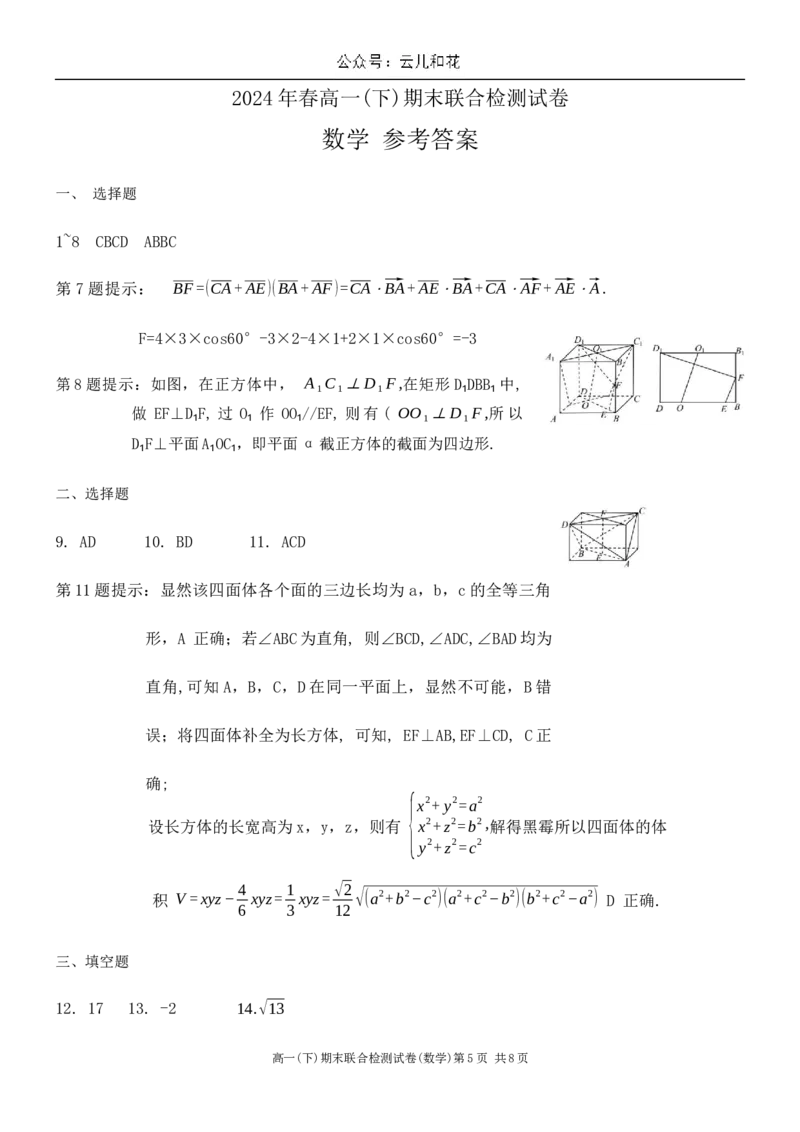
如 图 , 三 棱 柱 ABC−A₁B₁C₁中 , A₁ 在 底 面 ABC 内 的 射 影 为 △ABC的 外 心 O , 且
∠A₁AB=60°,AB=AC,BC=a,三棱柱的侧面积为 2√3a2.
(1) 求证: AA₁⊥BC;
(2)求三棱柱 ABC−A₁B₁C₁的体积;
(3) 分 别 求 二 面 角 B−AA₁−C和 二 面 角
A−BB₁−C的大小.
高一(下)期末联合检测试卷(数学)第4页 共8页2024 年春高一(下)期末联合检测试卷
数学 参考答案
一、 选择题
1~8 CBCD ABBC
第7题提示: BF=(CA+AE)(BA+AF)=CA⋅⃗BA+AE⋅⃗BA+CA⋅⃗AF+⃗AE⋅⃗A.
F=4×3×cos60°-3×2-4×1+2×1×cos60°=-3
第8题提示:如图,在正方体中, A₁C₁⊥D₁F,在矩形D₁DBB₁中,
做 EF⊥D₁F,过 O₁ 作 OO₁//EF,则有( OO₁⊥D₁F,所以
D₁F⊥平面A₁OC₁,即平面α截正方体的截面为四边形.
二、选择题
9. AD 10. BD 11. ACD
第11题提示:显然该四面体各个面的三边长均为 a,b,c的全等三角
形,A 正确;若∠ABC为直角, 则∠BCD,∠ADC,∠BAD均为
直角,可知A,B,C,D在同一平面上,显然不可能,B错
误;将四面体补全为长方体, 可知, EF⊥AB,EF⊥CD, C正
确;
{x2+ y2=a2
设长方体的长宽高为x,y,z,则有 x2+z2=b2,解得黑霉所以四面体的体
y2+z2=c2
4 1 √2
积 V =xyz− xyz= xyz= √(a2+b2−c2)(a2+c2−b2)(b2+c2−a2) D 正确.
6 3 12
三、填空题
12. 17 13. -2 14.√13
高一(下)期末联合检测试卷(数学)第5页 共8页第14题提示:由 可知, a,b夹角为 |3a-c|+|b-c|≥|3a-
1 2π
|2a−b|=√7 a⋅b=− , ,
2 3
c+c-b|=|3a-b|, 等 号 成 立 时 ,3a-c 与 c-b 同 向 , |3a-c|+|b-c| 的 最 小 值 为
√9a2−6a⋅b+b2=√13,如图所示.
四、解答题
15. (13分)
解: (1) 平均数为65×0.05+75×0.15+85×0.55+95×0.25=85 ……3分
0.3
设中位数为x,则有 (x−80)⋅0.055=0.5−0.05−0.15=0.3⇒x=80+ ≈85.5;…7分
0.055
(2)按比例, 从[60,70)范围内抽取1人,记为a, 从[70,80)范围内抽取3人, 记为b₁,b₂,b₃,从这4人
4×3
中抽取2人共 =6个基本事件, ……10分其中2
2
3 1
人不在同一评分区间有3个基本事件,从而概率为 = . ……13分
6 2
(另解:写出样本空间为:{(a,b₁),(a,b₂),(a,b₃),(b₁,b₂),(b₁,b₃),(b₂,b₃)},符合条件的样本
3 1
点为:(a,b₁),(a,b₂),(a,b₃).从而概率为 = .)
6 2
16. (15分)
解: (1)⃗OC=(1−t)⃗OA+t⃗OB, 有 ⃗OC−⃗OA=t(⃗OB−⃗OA),⃗AC=t⃗AB,所以A,B,C三点共线; …6分
(2) 设 ⃗OA=(1,0),⃗OB=(2cosθ,2sinθ),则 ⃗OP=(1−t,0),⃗OQ=(2tcosθ,2tsinθ), …8分
从而 PQ|2=(1−t−2tcosθ) 2+(2tsinθ) 2=t2(5+4cosθ)−2(1+2cosθ)t.+1 …11分
因为5+ −4cosθ>0,Δ=4(1+2cosθ)²−4(5+4cosθ)=16cos²θ−16≤0
1+2cosθ
当 t= 时 |⃗PQ|取最小值, …13分
5+4cosθ
1+2cosθ 2 1 π
有 = , 解得 cosθ= , 从而 θ= . …15分
5+4cosθ 7 2 3
17. (15分)证明:(1)取PC中点E,连接ME, BE, 因为M为DP中点, N为AB 中点,所以
1 1 1 1
ME CD且 ME= CD,又因为 BN CD且 BN= CD,所以
2 2 2 2
ME∥BN且ME=BN,
高一(下)期末联合检测试卷(数学)第6页 共8页所以四边形BEMN 为平行四边形, ……3分
所以MN∥BE,
因为MN⊄平面PBC, BE⊂平面PBC,
所以MN//平面PBC; ……6分
√2
(2) 因为 S =CB⋅CD⋅sinC=sinC= ,因为AC>BD, 所以, 解得
ABCD 2 ……8分
π π
∠DCB= ,因 为 ∠DCB=∠PCB= ,CD=PC,BC=BC,所 以
4 4 ……10分
△BCD≌△BCP,过 P 作 PQ⊥BC 于点 Q, 连接 DQ, 所以 DQ⊥BC,所
√2 √2
以 PQ=DQ=DC⋅ = ,PQ2+DQ2=1=PD2,所以 PQ⊥DQ, 又
2 2
PQ⊥BC, BC∩DQ=Q, 所以PQ⊥平面ABCD,因为PQ⊂ ……14分
平面PBC,
所以平面PBC⊥平面ABCD. ……15分
18. (17分)
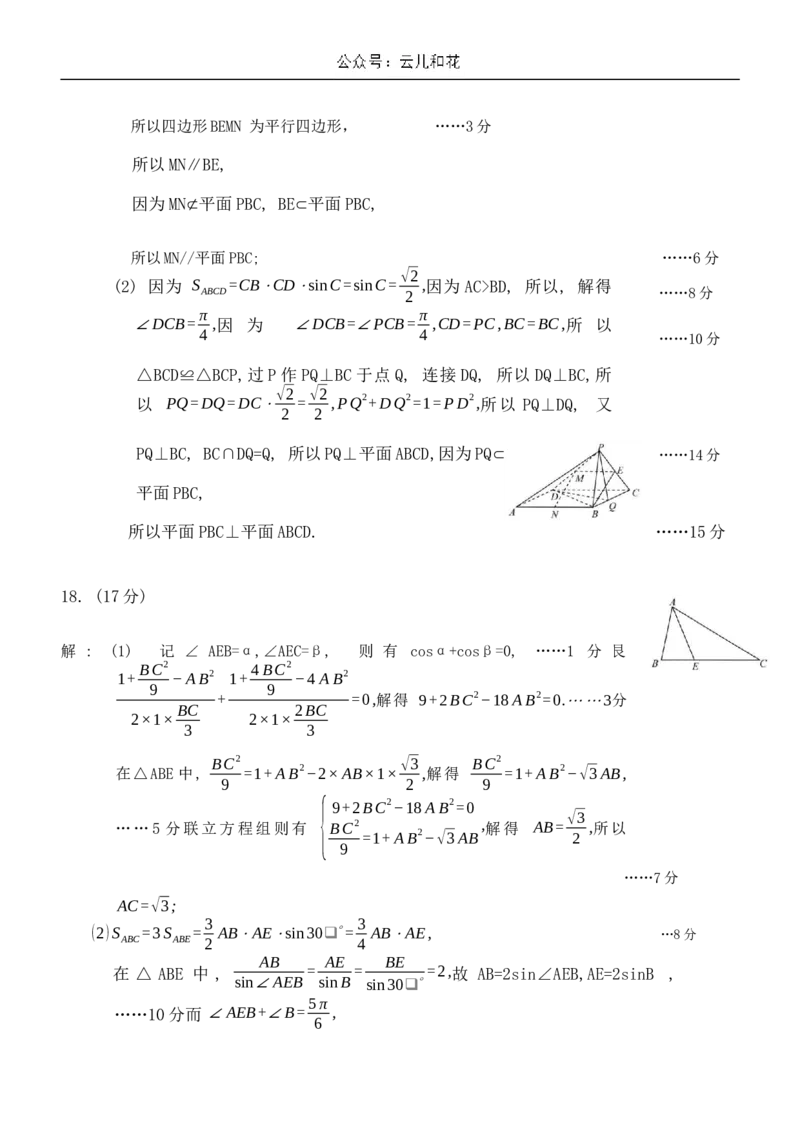
解 : (1) 记 ∠ AEB=α,∠AEC=β, 则 有 cosα+cosβ=0, ……1 分 艮
BC2 4BC2
1+ −AB2 1+ −4AB2
9 9
+ =0,解得 9+2BC2−18AB2=0.⋯⋯3分
BC 2BC
2×1× 2×1×
3 3
BC2 √3 BC2
在△ABE 中, =1+AB2−2×AB×1× ,解得 =1+AB2−√3AB,
9 2 9
{9+2BC2−18AB2=0
√3
……5 分联立方程组则有 BC2 ,解得 AB= ,所以
=1+AB2−√3AB 2
9
……7分
AC=√3;
3 3
(2)S =3S = AB⋅AE⋅sin30❑∘= AB⋅AE, …8分
ABC ABE 2 4
AB AE BE
在 △ ABE 中 , = = =2,故 AB=2sin∠AEB,AE=2sinB ,
sin∠AEB sinB sin30❑∘
5π
……10分而 ∠AEB+∠B= ,
6故 AB=2sin ( B+ π) ,S = 3 AB⋅AE=3 [ sin ( B+ π) ⋅sinB ] = 3 (√3sin2B+cosBsinB)
6 ABc 4 6 2
=
3(
√3
1−cos2B
+
sin2B)
=
3
(√3+sin2B−√3cos2B)=
3√3
+
3
sin
(
2B−
π)
,
2 2 2 4 4 2 3
( 5π) π ( π 4π)
……14 分 而 B∈ 0, ,2B− ∈ − , ,故
6 3 3 3
( π) ( √3 ] ( 6+3√3]
sin 2B− ∈ − ,1 ,S ∈ 0, .……17分
3 2 ABC 4
19. (17 分)
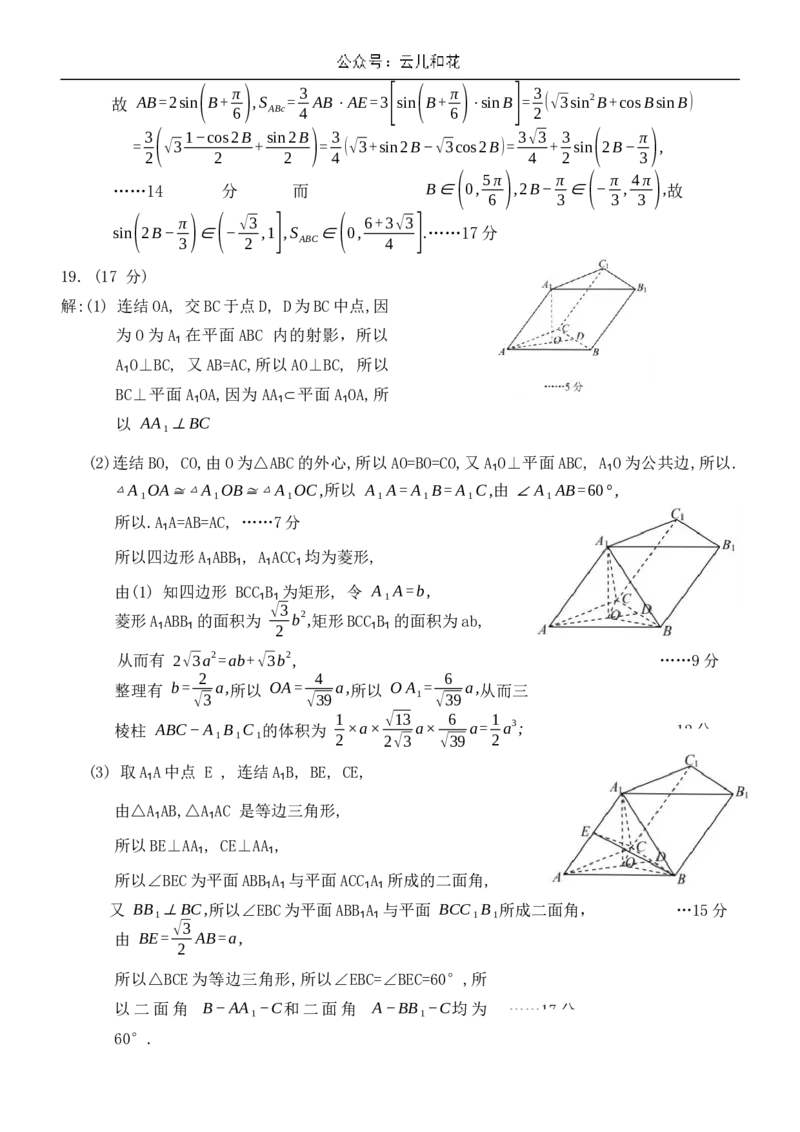
解:(1) 连结OA, 交BC于点D, D为BC中点,因
为O为A₁在平面ABC 内的射影,所以
A₁O⊥BC, 又AB=AC,所以AO⊥BC, 所以
BC⊥平面 A₁OA,因为AA₁⊂平面 A₁OA,所
以 AA₁⊥BC
(2)连结BO, CO,由O为△ABC的外心,所以AO=BO=CO,又A₁O⊥平面ABC, A₁O为公共边,所以.
△A₁OA≅△A₁OB≅△A₁OC,所以 A₁A=A₁B=A₁C,由 ∠A₁AB=60°,
所以.A₁A=AB=AC, ……7分
所以四边形A₁ABB₁, A₁ACC₁均为菱形,
由(1) 知四边形 BCC₁B₁为矩形, 令 A₁A=b,
√3
菱形A₁ABB₁的面积为 b2,矩形BCC₁B₁的面积为ab,
2
从而有 2√3a2=ab+√3b2, ……9分
2 4 6
整理有 b= a,所以 OA= a,所以 OA = a,从而三
√3 √39 1 √39
1 √13 6 1
棱柱 ABC−A₁B₁C₁的体积为 ×a× a× a= a3; ……12分
2 2√3 √39 2
(3) 取A₁A中点 E , 连结A₁B, BE, CE,
由△A₁AB,△A₁AC 是等边三角形,
所以BE⊥AA₁, CE⊥AA₁,
所以∠BEC为平面ABB₁A₁与平面ACC₁A₁所成的二面角,
又 BB₁⊥BC,所以∠EBC为平面ABB₁A₁与平面 BCC₁B₁所成二面角, …15分
√3
由 BE= AB=a,
2
所以△BCE为等边三角形,所以∠EBC=∠BEC=60°,所
以二面角 B−AA₁−C和二面角 A−BB₁−C均为 ……17分
60°.高一(下)期末联合检测试卷(数学)第8页 共8页