文档内容
高一(下)期末数学试卷
一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要
求的一项.
1.复数 ( )
A. B. C. D.
2.在平行四边形 中, 等于( )
A. B. C. D.
3.某中学高一年级有 人,高二年级有 人,高三年级有 人,为了解学校高中学生视力情况,现
用比例分配的分层随机抽样方法抽取一个容量为 的样本,则高一年级应抽取的人数为( )
A. B. C. D.
4.若单位向量 , 的夹角为 ,则 • =( )
A. 2 B. C. D. 1
5.若a和b是异面直线,a和c是平行直线,则b和c的位置关系是( )
A. 平行 B. 异面
C. 异面或相交 D. 相交、平行或异面
6.甲、乙、丙、丁四组人数分布如图所示,根据扇形统计图的情况可以知道丙、丁两组人数和为( )
A. 150 B. 250 C. 300 D. 4007.已知复数 满足 ,则 ( )
A. B. C. D.
8.若长方体所有顶点都在一个球面上,长、宽、高分别是3,2,1,则这个球面的面积为( )
A. 9π B. 12π C. 14π D. 18π
9.设 为非零向量,则“ ”是“ 与 共线” 的( )
A. 充分而不必要条件 B. 必要而不充分条件
.
C 充要条件 D. 既不充分也不必要条件
10.已知△ABC是等腰三角形,AB=AC=5,BC=6,点P在线段AC上运动,则| + |的取值范围是
( )
A. [3,4] B. C. [6,8] D.
二、填空题共5小题,每小题5分,共25分.
11.设复数z=1+i,则z的模|z|=_____.
12.数据19,20,21,23,25,26,27,则这组数据的方差是_____.
13.三棱锥的三条侧棱两两垂直,长分别为1,2,3,则这个三棱锥的体积为_____.
14.已知 =(1,2), =(2,y),| + |=| - |,则y=_____.
15. 在中, , .
①若 ,则角 的大小为_____;
②若角 有两个解,则 的取值范围是_____.
三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.
16.已知复数 在复平面内对应点 .
(1)若 ,求 ;
(2)若点 在直线 上,求 的值.
.
17.已知三个点 , ,(1)求证: ;
(2)若四边形 为矩形,求点 的坐标及矩形 两对角线所成锐角的余弦值.
18.为了解某小区 月用电量情况,通过抽样,获得了 户居民 月用电量(单位:度),将数据按照
、 、 、 分成六组,制成了如图所示的频率分布直方图.
(1)求频率分布直方图中 的值;
(2)已知该小区有 户居民,估计该小区 月用电量不低于 度的户数,并说明理由;
(3)估计该小区 的居民 月用电量的值,并说明理由.
19.如图,在△ABC中,∠ABC=90°,AB=4,BC=3,点D在线段AC上,且AD=4DC.
(1)求BD的长;
(2)求sin∠BDC 的值.
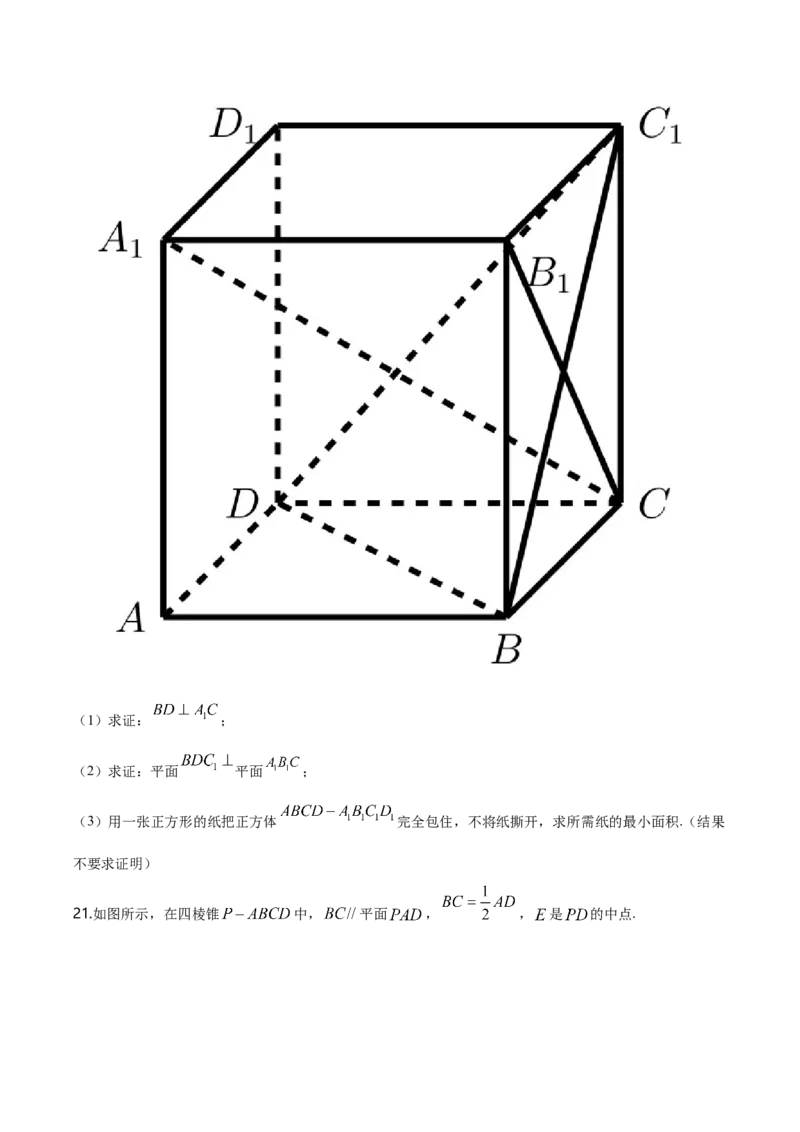
20.如图所示,在正方体 中, .(1)求证: ;
(2)求证:平面 平面 ;
(3)用一张正方形的纸把正方体 完全包住,不将纸撕开,求所需纸的最小面积.(结果
不要求证明)
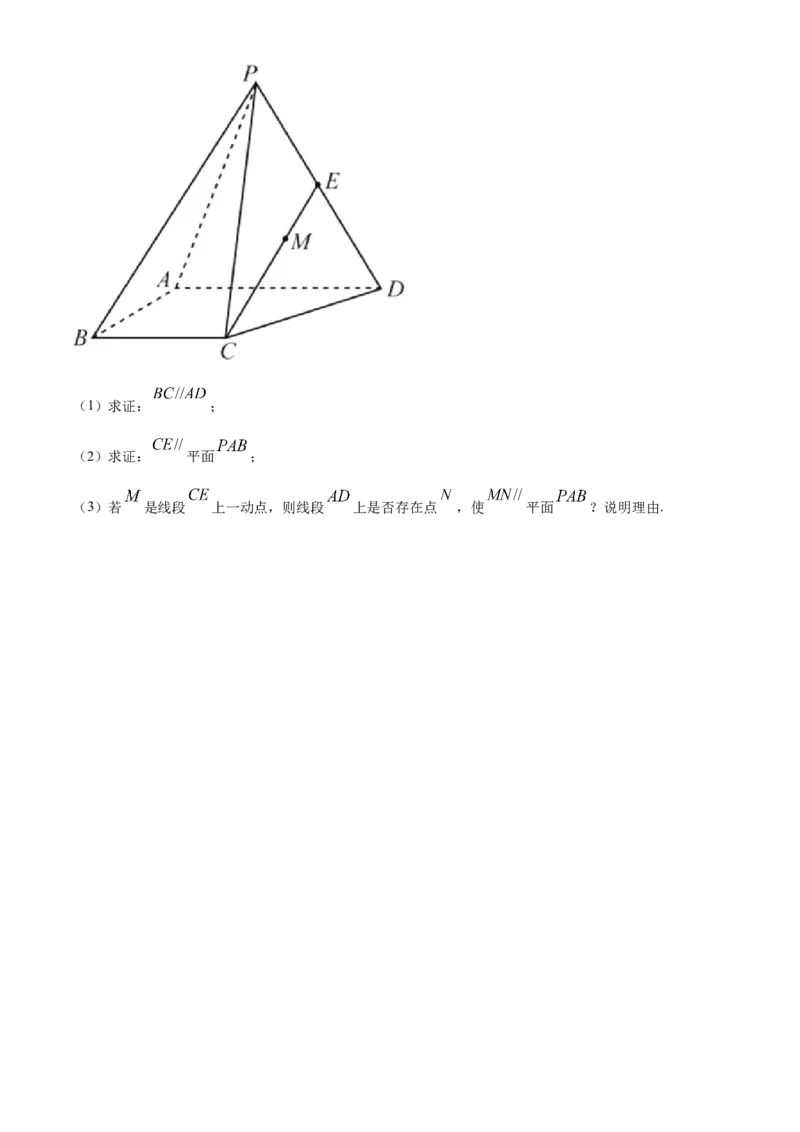
21.如图所示,在四棱锥 中, 平面 , , 是 的中点.(1)求证: ;
(2)求证: 平面 ;
(3)若 是线段 上一动点,则线段 上是否存在点 ,使 平面 ?说明理由.