文档内容
高一第二学期数学期中考试
注意事项:
1.时间为120分钟,满分150分.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.
2.在答题卡上与题号相对应的答题区域内答题,写在试卷、草稿纸上或答题卡非题号对应的
答题区域的答案一律无效.不得用规定以外的笔和纸答题,不得在答题卡上做任何标记.
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 复数z满足 ,则z的共轭复数为( )
A. B. C. D.
的
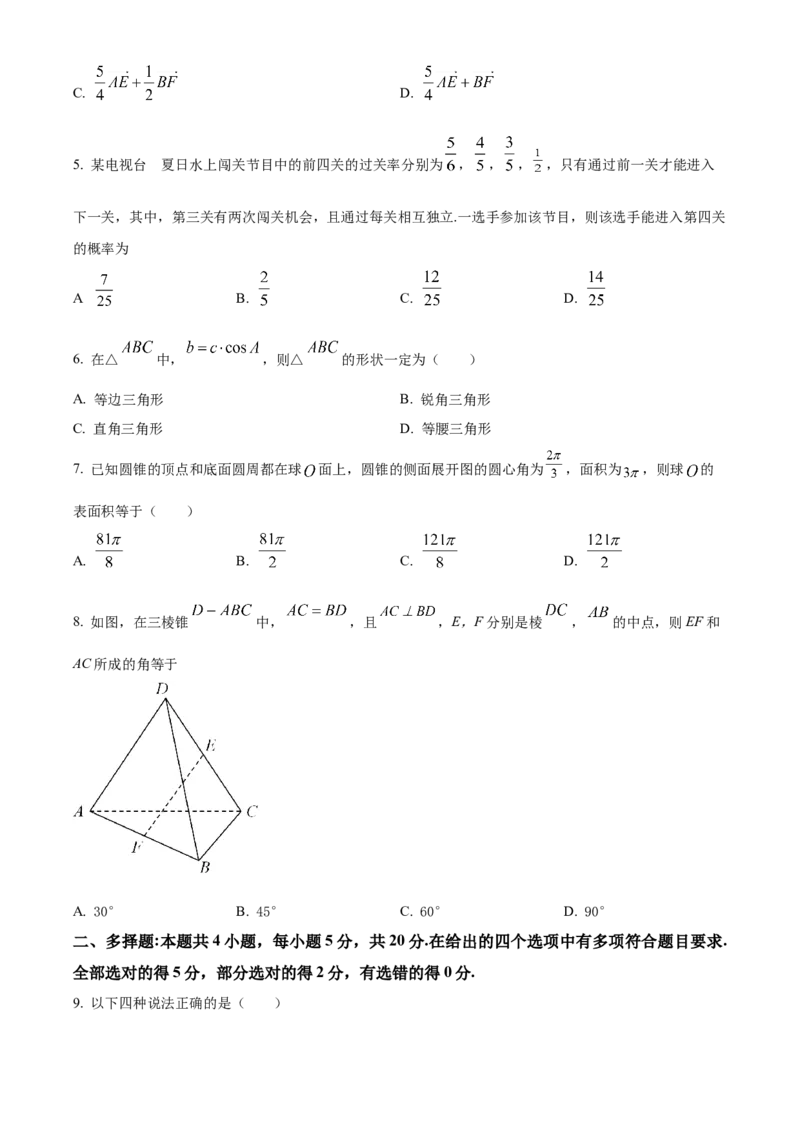
2. 如图,用斜二测画法得到一个水平放置 平面图形,其直观图是一个底角为45°,腰长为 ,上底为1
的等腰梯形,那么原平面图形的最长边长为( )
A. B. C. 2 D. 3
3. 设平面向量 , ,若 ,则 ( )
A. 1 B. 2 C. -1 D. 3
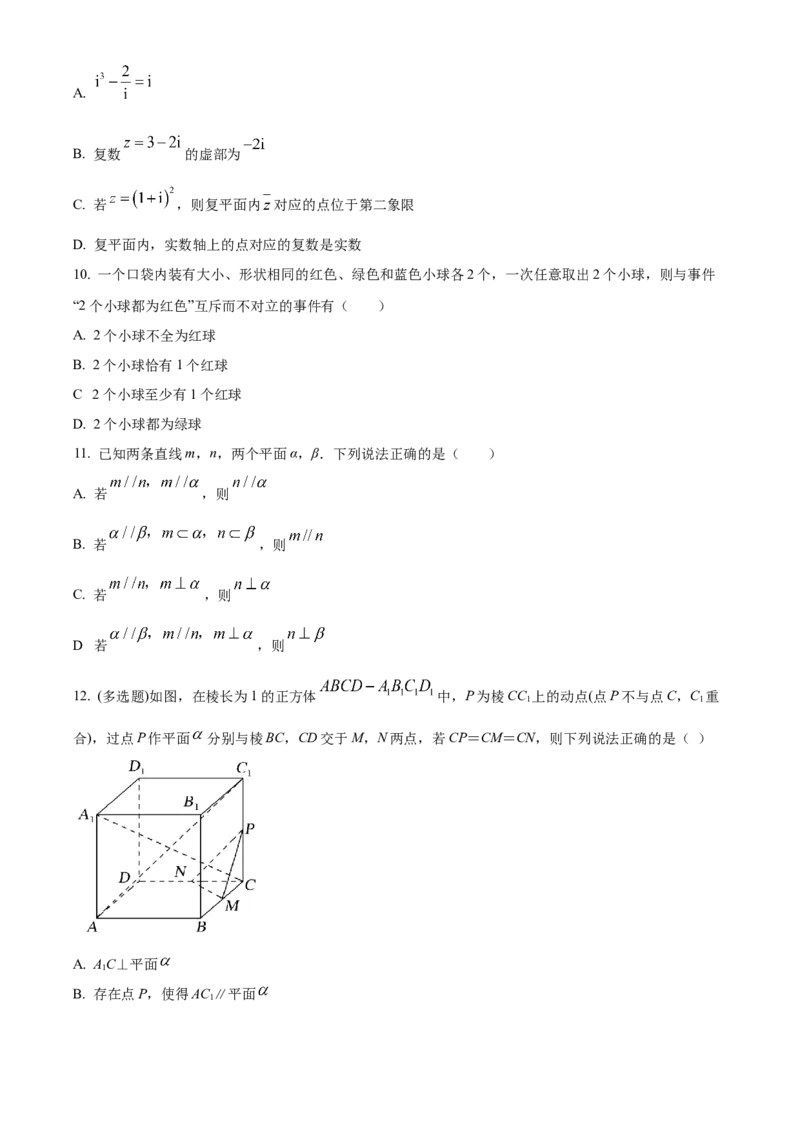
4. 如图所示,平行四边形 中, ,点F为线段AE的中点,则 ( )
A. B.C. D.
5. 某电视台 夏的日水上闯关节目中的前四关的过关率分别为 , , , ,只有通过前一关才能进入
下一关,其中,第三关有两次闯关机会,且通过每关相互独立.一选手参加该节目,则该选手能进入第四关
的概率为
.
A B. C. D.
6. 在△ 中, ,则△ 的形状一定为( )
A. 等边三角形 B. 锐角三角形
C. 直角三角形 D. 等腰三角形
7. 已知圆锥的顶点和底面圆周都在球 面上,圆锥的侧面展开图的圆心角为 ,面积为 ,则球 的
表面积等于( )
A. B. C. D.
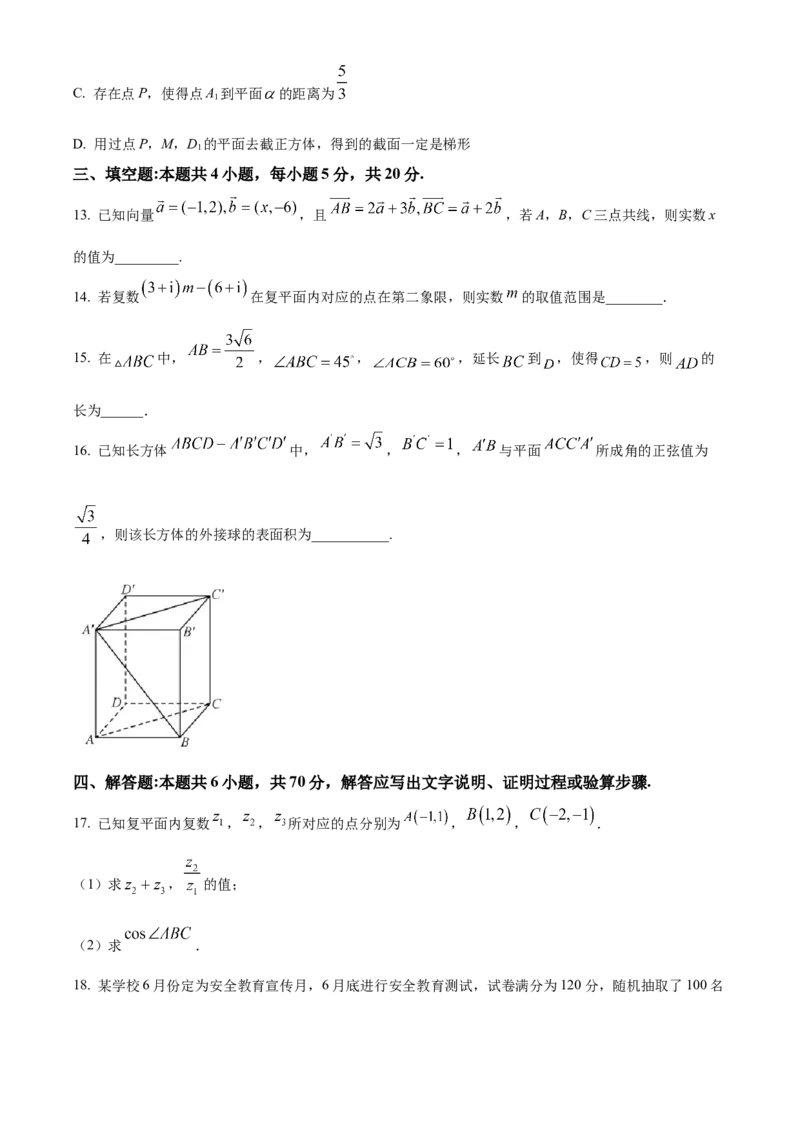
8. 如图,在三棱锥 中, ,且 ,E,F分别是棱 , 的中点,则EF和
AC所成的角等于
A. 30° B. 45° C. 60° D. 90°
二、多择题:本题共4小题,每小题5分,共20分.在给出的四个选项中有多项符合题目要求.
全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 以下四种说法正确的是( )A.
B. 复数 的虚部为
C. 若 ,则复平面内 对应的点位于第二象限
D. 复平面内,实数轴上的点对应的复数是实数
10. 一个口袋内装有大小、形状相同的红色、绿色和蓝色小球各2个,一次任意取出2个小球,则与事件
“2个小球都为红色”互斥而不对立的事件有( )
A. 2个小球不全为红球
B. 2个小球恰有1个红球
.
C 2个小球至少有1个红球
D. 2个小球都为绿球
11. 已知两条直线m,n,两个平面α,β.下列说法正确的是( )
A. 若 ,则
B. 若 ,则
C. 若 ,则
.
D 若 ,则
12. (多选题)如图,在棱长为1的正方体 中,P为棱CC 上的动点(点P不与点C,C 重
1 1
合),过点P作平面 分别与棱BC,CD交于M,N两点,若CP=CM=CN,则下列说法正确的是( )
A. AC⊥平面
1
B. 存在点P,使得AC ∥平面
1C. 存在点P,使得点A 到平面 的距离为
1
D. 用过点P,M,D 的平面去截正方体,得到的截面一定是梯形
1
三、填空题:本题共4小题,每小题5分,共20分.
13. 已知向量 ,且 ,若A,B,C三点共线,则实数x
的值为_________.
14. 若复数 在复平面内对应的点在第二象限,则实数 的取值范围是________.
15. 在 中, , , ,延长 到 ,使得 ,则 的
长为______.
16. 已知长方体 中, , , 与平面 所成角的正弦值为
,则该长方体的外接球的表面积为___________.
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或验算步骤.
17. 已知复平面内复数 , , 所对应的点分别为 , , .
(1)求 , 的值;
(2)求 .
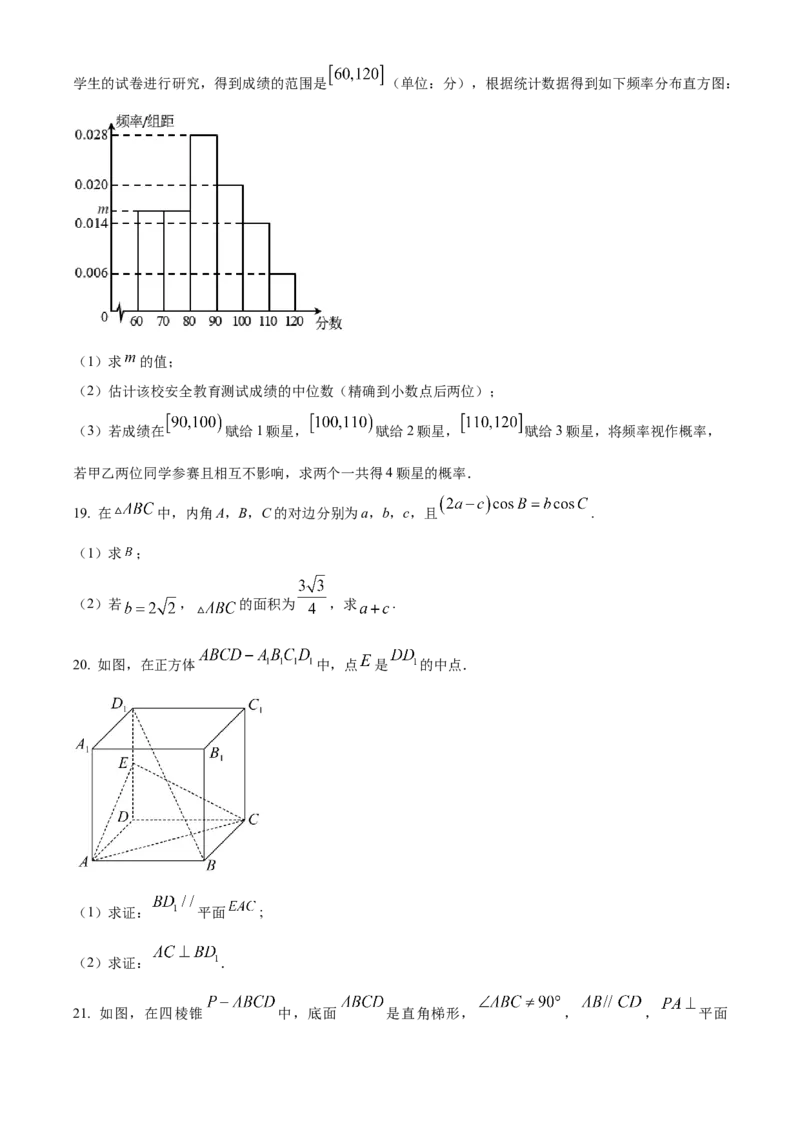
18. 某学校6月份定为安全教育宣传月,6月底进行安全教育测试,试卷满分为120分,随机抽取了100名学生的试卷进行研究,得到成绩的范围是 (单位:分),根据统计数据得到如下频率分布直方图:
(1)求 的值;
(2)估计该校安全教育测试成绩的中位数(精确到小数点后两位);
(3)若成绩在 赋给1颗星, 赋给2颗星, 赋给3颗星,将频率视作概率,
若甲乙两位同学参赛且相互不影响,求两个一共得4颗星的概率.
19. 在 中,内角A,B,C的对边分别为a,b,c,且 .
(1)求 ;
(2)若 , 的面积为 ,求 .
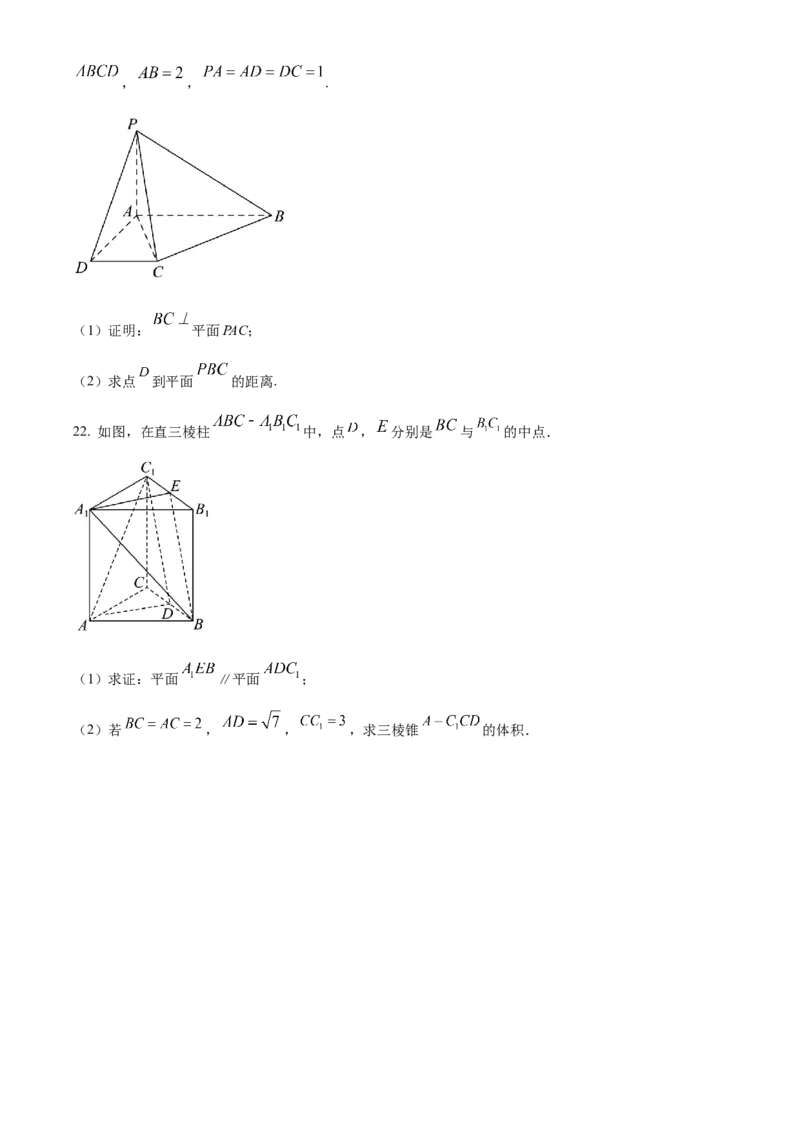
20. 如图,在正方体 中,点 是 的中点.
(1)求证: 平面 ;
(2)求证: .
21. 如图,在四棱锥 中,底面 是直角梯形, , , 平面, , .
(1)证明: 平面PAC;
(2)求点 到平面 的距离.
22. 如图,在直三棱柱 中,点 , 分别是 与 的中点.
(1)求证:平面 ∥平面 ;
(2)若 , , ,求三棱锥 的体积.