文档内容
第二学期期中考试
高一数学
注意事项:
1.答卷前,考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡的相应位置上.
将条形码横贴在答题卡“条形码粘贴处”.
2.作答选择题时,选出每小题答案后,用2B铅笔将答题卡对应题目选项的答案信息点涂黑;
如需改动,用橡皮擦干净后,再涂其他答案.答案涂在试卷上一律无效.
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内;
如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液.不按以上要求作
答无效.
4.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1. 设 是虚数单位,若复数 ,则 ( )
A. B. C. D.
【答案】C
【解析】
【分析】
由已知条件求出复数 ,利用复数的模的公式可求得 .
【详解】 , ,
因此, .
故选:C.
.
2 已知向量 , , ,且 ,则 ( )
A. 1 B. 2 C. 3 D. 4
【答案】A
【解析】
学科网(北京)股份有限公司【分析】先求出 ,再结合 ,通过数量积的坐
标运算求 即可.
【详解】由题意知: ,由
可得 ,即 ,又 ,解得 .
故选:A.
3. 已知i为虚数单位,复数 ,则 ( )
A. B. C. D. 0
【答案】C
【解析】
【分析】先由复数的除法运算计算出 ,再按照乘方运算计算即可.
【详解】 ,则 ,
, ,故
.
故选:C.
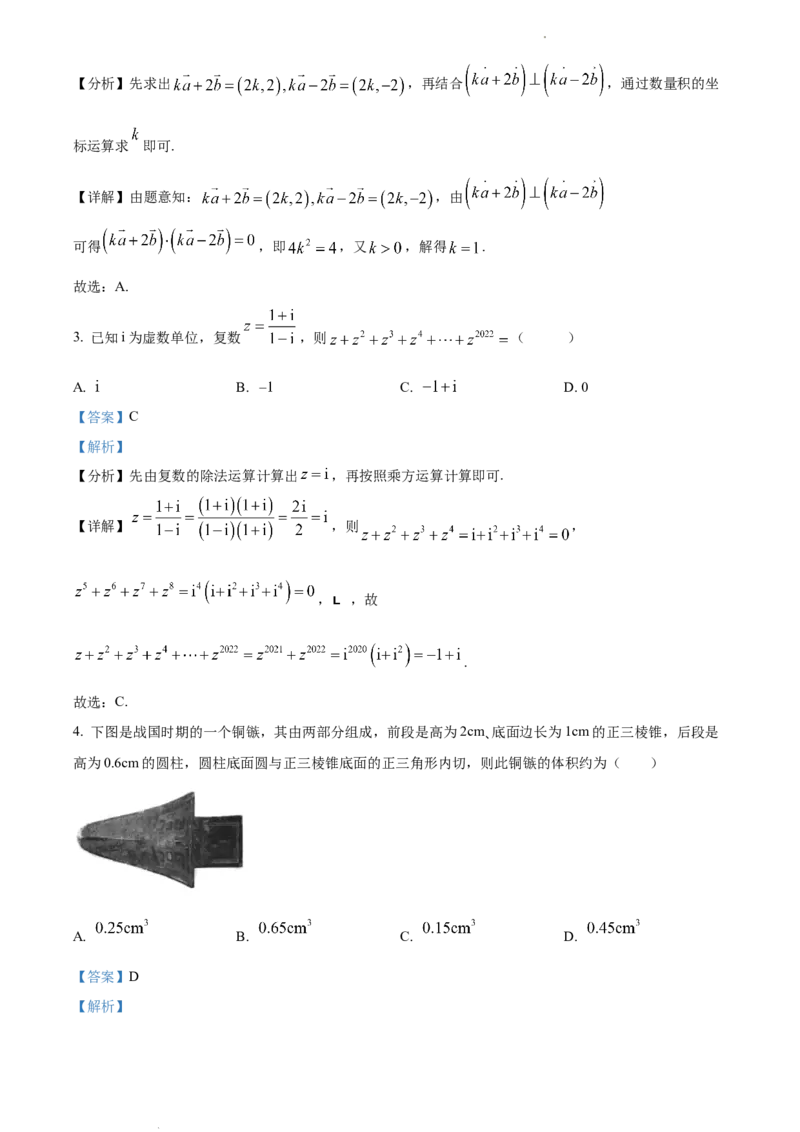
4. 下图是战国时期的一个铜镞,其由两部分组成,前段是高为2cm、底面边长为1cm的正三棱锥,后段是
高为0.6cm的圆柱,圆柱底面圆与正三棱锥底面的正三角形内切,则此铜镞的体积约为( )
A. B. C. D.
【答案】D
【解析】
学科网(北京)股份有限公司【分析】先求出内切圆半径为r,再分别利用三棱锥体积与圆柱体积公式即可求出总体积.
【详解】因为正三棱锥的底面边长为1,设其内切圆半径为r,由等面积法,可得:
,解得: ,所以其内切圆半径为 .
由三棱锥体积与圆柱体积公式可得: .
故选:D.
5. 用斜二测画法画水平放置的平面图形的直观图时,下列说法正确的是( )
A. 相等的线段在直观图中仍相等 B. 水平放置的三角形的直观图仍是三角形
C. 相等的角在直观图中仍相等 D. 水平放置的菱形的直观图仍是菱形
【答案】B
【解析】
【分析】由如图所示正方形及直观图即可判断A、C、D选项;结合斜二测画法的定义判断B选项.
详解】
【
如图所示为正方形 及其直观图 ,显然 ,A错误;
,C错误;
正方形是特殊的菱形,直观图为平行四边形,D错误;水平放置的三角形的直观图仍是三角形,B正确.
故选:B.
6. 已知圆锥的表面积为3π,其侧面展开图是一个半圆,则该圆锥的底面半径为( )
A. 2 B. 1 C. D.
【答案】B
【解析】
学科网(北京)股份有限公司【分析】设圆锥的母线长为 ,底面半径为 ,利用侧面展开图得到 ,然后由侧面积公式,列式求
解 即可.
【详解】解:设圆锥的母线长为 ,底面半径为 ,因为圆锥的侧面展开图为一个半圆,
所以 ,则 ,又圆锥的表面积为 ,则 ,
解得: .
故选:B.
7. 若正四面体的表面积为 ,则其体积为( )
A. B. C. D.
【答案】D
【解析】
【分析】计算出正四面体的棱长,将正四面体补成正方体,计算出正方体的棱长,即可求得正四面体的体
积.
【详解】设正四面体 的棱长为 ,则该正四面体的表面积为 ,可得 .
将正四面体 补成正方体 ,则正方体 的棱长为 ,
所以, .
故选:D.
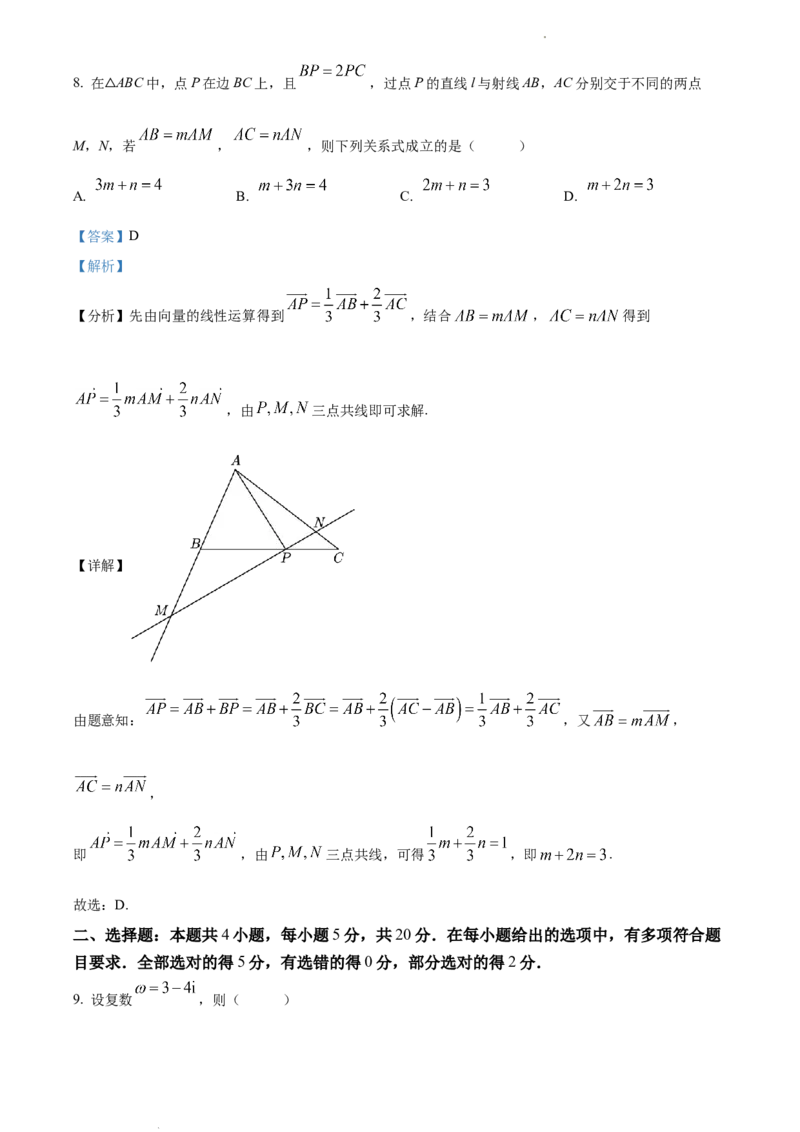
学科网(北京)股份有限公司8. 在 ABC中,点P在边BC上,且 ,过点P的直线l与射线AB,AC分别交于不同的两点
△
M,N,若 , ,则下列关系式成立的是( )
A. B. C. D.
【答案】D
【解析】
【分析】先由向量的线性运算得到 ,结合 , 得到
,由 三点共线即可求解.
【详解】
由题意知: ,又 ,
,
即 ,由 三点共线,可得 ,即 .
故选:D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9. 设复数 ,则( )
学科网(北京)股份有限公司A. 的虚部为 B. 的共轭复数为
C. 在复平面内对应的点在第四象限 D. 若复数z满足 ,则 的最大值为6
【答案】BCD
【解析】
【分析】根据复数的相关概念判断A、B、C,设 , ,根据复数模的几何意义求出
的最大值;
【详解】解:复数 的虚部为 ,共轭复数为 ,
在复平面内所对应的点的坐标为 位于第四象限,故A错误,B、C正确;
设 , ,由 ,即 ,
则 表示圆上 上的点 到点 的距离,
因为 ,所以 ,即 的最大值为 ,故D正确;
故选:BCD
10. ABC中,a,b,c分别为角A,B,C的对边.根据以下条件解三角形,恰有一解的是( )
△
A. , , B. , ,
C. , , D. , ,
【答案】AC
【解析】
【分析】由正弦定理依次判断4个选项中三角形解的个数即可.
【详解】对于A,由正弦定理得 ,即 ,解得 ,又 ,
只有一解,正确;
学科网(北京)股份有限公司对于B,由正弦定理得 ,即 ,解得 ,又 ,有两解,错误;
对于C,由正弦定理得 ,即 ,解得 ,又 ,只有一解,
正确;
对于D,由正弦定理得 ,即 ,解得 ,无解,错误.
故选:AC.
11. 如图,正方形 的边长为1cm,它是水平放置的一个平面四边形OABC的直观图,则关于平面
四边形OABC有( )
A. 图形为矩形 B. 周长为8 C. 边OC的长度为2 D. 面积为
【答案】BD
【解析】
【分析】还原出原图,根据直观图与原图的长度关系,即可求得 , 的值,代入公式,即可得答案.
【详解】把直观图 还原为原图形 ,如图所示,所以原图形 为平行四边形,故A错;
学科网(北京)股份有限公司根据题意, , , ,平面四边形OABC的周长为:
,故B正确,C错误;
所以平行四边形 的面积 ,故D正确.
故选:BD.
12. ABC中,a,b,c分别为角A,B,C的对边,R是 ABC的外接圆半径,则( )
△ △
A.
B. 若 ,则
C.
D. 点G在 ABC所在平面内,若 ,则G是 ABC的外心
△ △
【答案】AC
【解析】
【分析】在三角形中,由正弦定理、余弦函数的单调性可判断A,由正弦函数的性质及三角形中角的范围
可判断B,根据三角恒等变换及正弦定理可判断C,由向量的运算及重心的性质可判断D.
【详解】 ABC中, ,
△
,
当 , ,
学科网(北京)股份有限公司当 , ,
当 时, ,综上, ,故A正确;
ABC中, 或 ,所以 或 ,故B错误;
△
由正弦定理 ,
,故C正确;
设 是 的中点,由 可得 ,即 , 是△ABC的重心,
故D错误.
故选:AC
三、填空题:本题共4小题,每小题5分,共20分.
13. 已知复数 ,则 __________.
【答案】
【解析】
【分析】
根据共轭复数的概念,先得到 ,再由复数的乘法运算,即可得出结果.
【详解】因为 ,所以 ,
因此 .
故答案为: .
【点睛】本题主要考查共轭复数的相关计算,属于基础题型.
14. 已知复数 为纯虚数,若 (其中 为虚数单位),则实数 的值为___________.
学科网(北京)股份有限公司【答案】 ##
【解析】
【分析】先利用复数的除法运算化简 ,再根据实部等于 虚部不等于 即可求得 的值.
【详解】由 可得 ,
若 为纯虚数,则 可得 ,
故答案为: .
15. 已知向量 , ,则 在 上的投影向量 __________.
【答案】
【解析】
【分析】直接由投影向量的公式求解即可.
【详解】由题意知: 在 上的投影向量 .
故答案为: .
16. 水平桌面上放置了三个半径为6的球,这三个球两两相切,在三个球共同的下方再放置一个小球,小
球与原来的三个球以及桌面都相切,则小球的半径为__________.
【答案】2
【解析】
【分析】先判断出三个球的球心与桌面的三个切点构成了正三棱柱 ,作出小球球心 在上
下底面的投影,通过相切求出 及 ,再通过勾股定理解出半径即可.
学科网(北京)股份有限公司【详解】
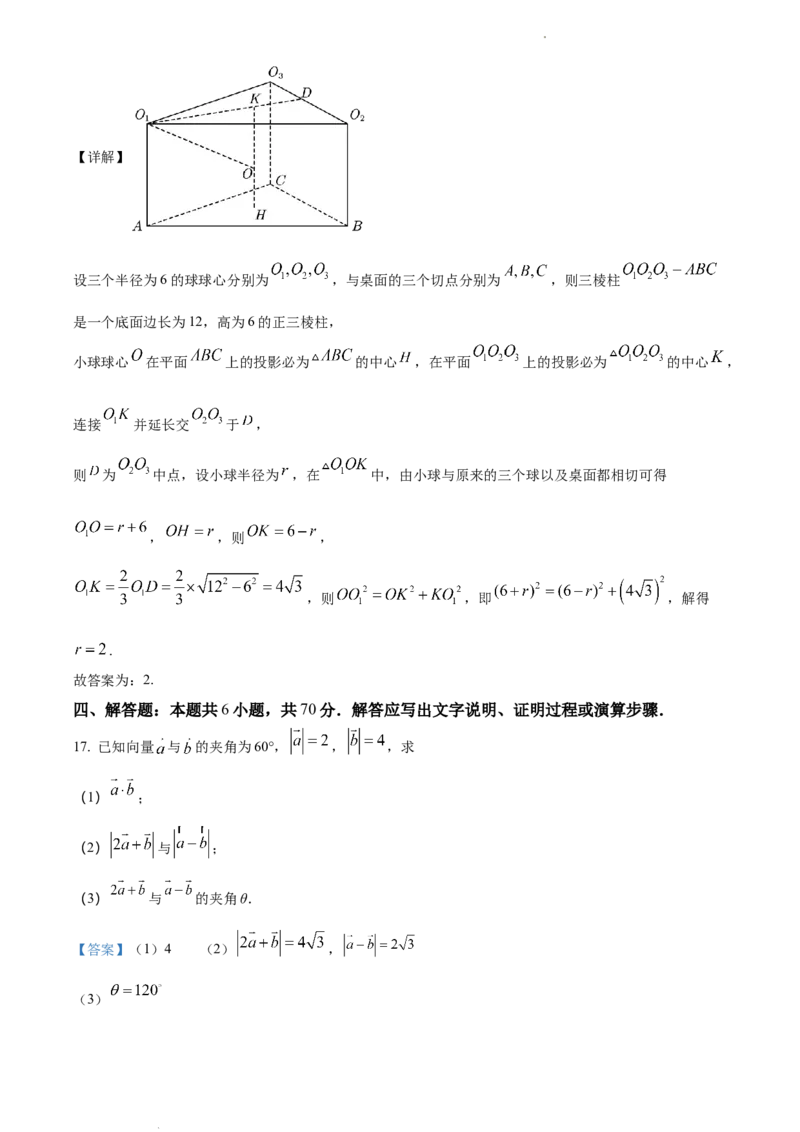
设三个半径为6的球球心分别为 ,与桌面的三个切点分别为 ,则三棱柱
是一个底面边长为12,高为6的正三棱柱,
小球球心 在平面 上的投影必为 的中心 ,在平面 上的投影必为 的中心 ,
连接 并延长交 于 ,
则 为 中点,设小球半径为 ,在 中,由小球与原来的三个球以及桌面都相切可得
, ,则 ,
,则 ,即 ,解得
.
故答案为:2.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 已知向量 与 的夹角为60°, , ,求
(1) ;
(2) 与 ;
(3) 与 的夹角θ.
【答案】(1)4 (2) ,
(3)
学科网(北京)股份有限公司【解析】
【分析】(1)直接由数量积的定义计算即可;
(2)先计算出 , ,再计算 与 即可;
(3)先计算出 ,再由夹角公式计算余弦值,进而求得夹角θ.
【小问1详解】
.
【小问2详解】
, ,
, .
【小问3详解】
, ,
又 ,则 .
18. 已知关于x的实系数一元二次方程 有两个虚根α,β.
(1)求m的取值范围;
(2)若 ,求m的值及 .
【答案】(1)
(2)1,
【解析】
【分析】(1)根据 列出不等式求解即可;
学科网(北京)股份有限公司(2)根据韦达定理可求出 的值,然后表示出 ,代入即可求解.
【小问1详解】
由已知得 ,
则 .
【小问2详解】
由 知 ,
则 .
由 得 ,
则 ,
故 .
19. 位于唐山市中心区的凤凰山,山势挺拔秀丽,苍松翠柏密布,因前山如凤凰展翅故名.古朴典雅的八
角重檐凤凰亭矗立在山巅,登二楼平台眺望,唐山美景一览无余.某测量小组为测量山的高度,建立了如
图所示的数学模型三棱锥C–OAB,OC垂直水平面OAB,点C代表凤凰亭的上顶点,A,B两点代表山脚
地面上的两个观测点,同学甲在A处测得仰角为45°,同学乙在B处测得仰角为30°,同学丙测得两个观测
点之间的距离AB为90米.(附:若一条直线垂直一个平面,则这条直线垂直于这个平面内的任意一条直
线.)
(1)求 ;
(2)同学甲测出∠CAB为钝角,同学乙测算出 ,求山高的近似值OC.
学科网(北京)股份有限公司【答案】(1) ;
(2)90米.
【解析】
【分析】(1)在 与 中,求出AC,BC与OC的关系,再利用正弦定理计算作答.
(2)在 中,利用余弦定理列方程,求解并验证作答.
【小问1详解】
在 中,由 得 ,在 中,由 得 ,
在 中,利用正弦定理得: ,所以 .
【小问2详解】
在 中,利用余弦定理得: ,
即 ,化简为 ,
解得 ,或 ,当 时, ,与 为钝角矛盾,经验证
符合条件,
所以山高的近似值OC为90米.
的
20. 如图,在边长为4 正三角形ABC中,E,F分别是边AB,AC上的点, , ,
, ,垂足分别是D,H,G,将 ABC绕AD所在直线旋转180°.
△
(1)由图中阴影部分旋转形成的几何体的体积记为V,当E,F分别为边AB,AC的中点时,求V;
学科网(北京)股份有限公司(2)由内部空白部分旋转形成的几何体侧面积记为S,当E,F分别在什么位置时,S最大?
【答案】(1)
(2)E,F分别为AB,AC的中点时S最大
【解析】
【分析】(1)依题意可得阴影部分旋转后的几何体是一个圆锥挖去一个圆柱,根据圆锥、圆柱的体积公
式计算可得;
(2)设 , ,表示出 ,则旋转图的侧面积 ,再利用基本不等式计
算可得;
【小问1详解】
解:由圆锥与圆柱的定义可知,将 绕AD旋转180°,
阴影部分旋转后的几何体是一个圆锥挖去一个圆柱,且圆锥的底面半径为2,高为 ,圆柱的底面半径
为1,高为 .
因此阴影部分形成的几何体的体积为 .
【小问2详解】
解:设 , ,则 , ,
此时 ,.
当且仅当 时等号成立,即E,F分别为AB,AC的中点时S最大.
21. ABC中,角A,B,C的对边分别为a,b,c,已知 .
△
(1)求B;
(2)若 ,求b的取值范围.
【答案】(1)
学科网(北京)股份有限公司(2)
【解析】
【分析】(1)由正弦定理及 得 ,进而得到 ,
即可求出 ;
(2)由余弦定理结合基本不等式即可求出b的取值范围.
【
小问1详解】
由正弦定理及 可得 ,又 ,
则 ,即 ,
则 ,因为 ,所以 , ,因为 ,
所以 .
【小问2详解】
由余弦定理得 ,因为 , ,所以 ,当且仅
当 时取等号.
又因为 ,所以 .综上所述, ,b的取值范围是 .
22. 某公园规划一个三角形的草坪区域,如图,AB长50米,BC长80米,AC长70米,中间需要设计一条
长为100米的雨花石折线小路BPC(点缀在草坪内部,不影响草坪面积).
(1)求∠ABC及 ;
学科网(北京)股份有限公司(2)当点P在什么位置时,小路内侧草坪( PBC)的面积最大?求出最大值.
△
【答案】(1) ,
(2)点P在草坪△ABC内部,最大值可以取到1200平方米
【解析】
【分析】(1)先由余弦定理求出 ,再由正弦定理可求得 .
(2)设 , ,则 ,设 ,由余弦定理得 ,
两式联立求解可得 ,则 ,再结合题意求得 的范围,即可求出 PBC的
△
面积最大.
【小问1详解】
由余弦定理得: ,则 ,
由正弦定理得 ,
可得 .
【小问2详解】
设 , ,则 .①
设 ,由余弦定理得 ,②
由①2-②得 ,即 ,
则 ,
因为 ,当且仅当 “ ”时取等,且 .
学科网(北京)股份有限公司所以 .
设 , ,则 , ,且 ,
于是当 时, 取得最大值1200平方米.
此时, , .
由(1)知 ,则 .
此时,点P在草坪△ABC内部,最大值可以取到1200平方米.
学科网(北京)股份有限公司