文档内容
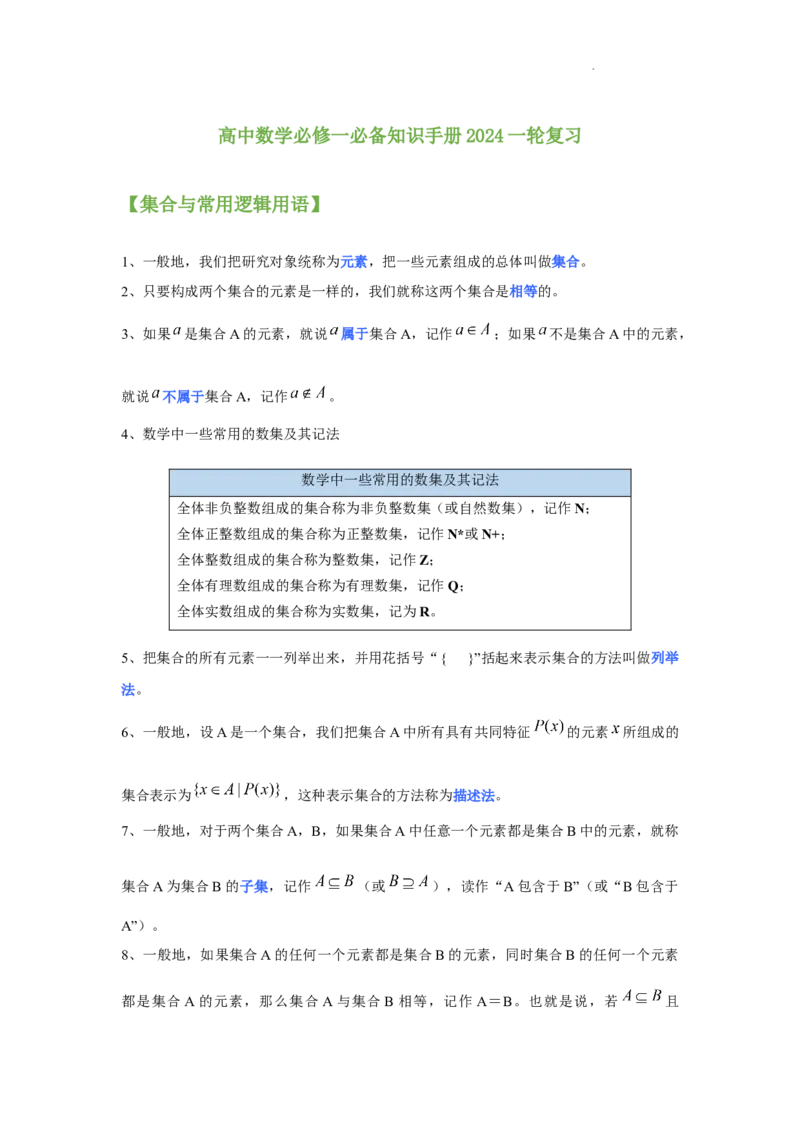
高中数学必修一必备知识手册2024一轮复习
【集合与常用逻辑用语】
1、一般地,我们把研究对象统称为元素,把一些元素组成的总体叫做集合。
2、只要构成两个集合的元素是一样的,我们就称这两个集合是相等的。
3、如果 是集合A的元素,就说 属于集合A,记作 ;如果 不是集合A中的元素,
就说 不属于集合A,记作 。
4、数学中一些常用的数集及其记法
数学中一些常用的数集及其记法
全体非负整数组成的集合称为非负整数集(或自然数集),记作N;
全体正整数组成的集合称为正整数集,记作N*或N+;
全体整数组成的集合称为整数集,记作Z;
全体有理数组成的集合称为有理数集,记作Q;
全体实数组成的集合称为实数集,记为R。
5、把集合的所有元素一一列举出来,并用花括号“{ }”括起来表示集合的方法叫做列举
法。
6、一般地,设A是一个集合,我们把集合A中所有具有共同特征 的元素 所组成的
集合表示为 ,这种表示集合的方法称为描述法。
7、一般地,对于两个集合A,B,如果集合A中任意一个元素都是集合B中的元素,就称
集合A为集合B的子集,记作 (或 ),读作“A包含于B”(或“B包含于
A”)。
8、一般地,如果集合A的任何一个元素都是集合B的元素,同时集合B的任何一个元素
都是集合A的元素,那么集合 A与集合B相等,记作 A=B。也就是说,若 且
学科网(北京)股份有限公司,则A=B。
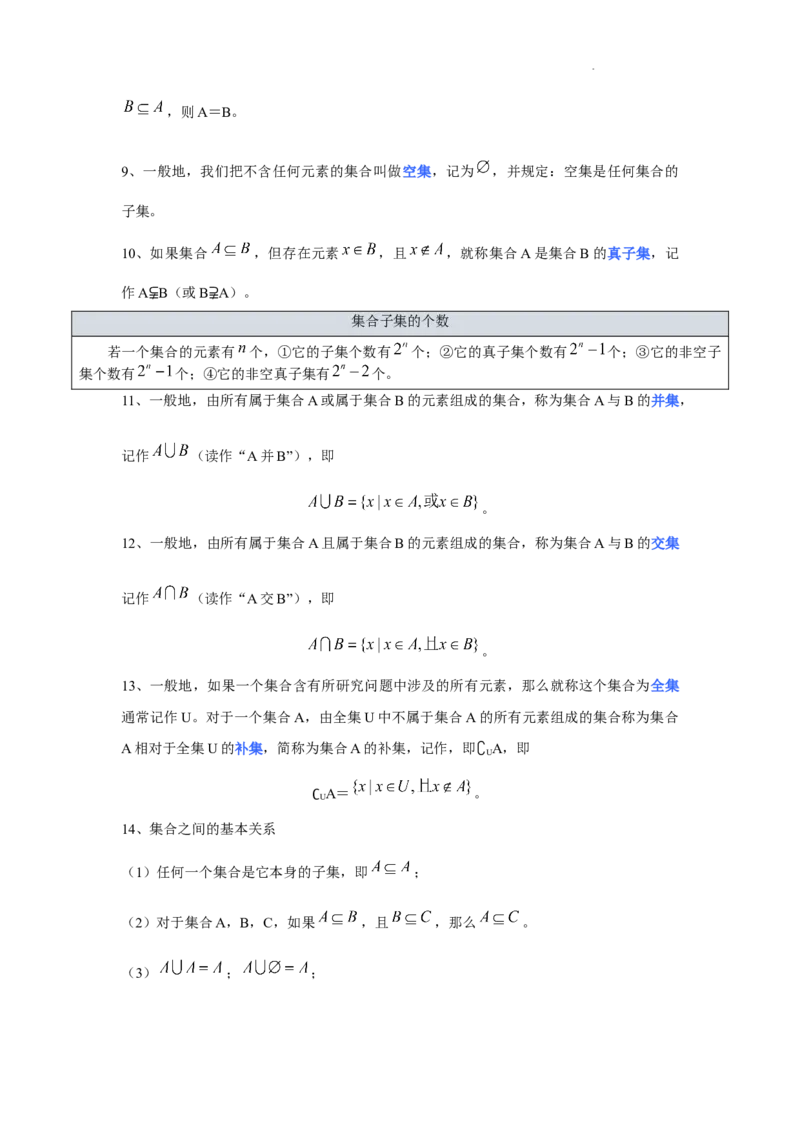
9、一般地,我们把不含任何元素的集合叫做空集,记为 ,并规定:空集是任何集合的
子集。
10、如果集合 ,但存在元素 ,且 ,就称集合A是集合B的真子集,记
作A B(或B A)。
集合子集的个数
⫋ ⫌
若一个集合的元素有 个,①它的子集个数有 个;②它的真子集个数有 个;③它的非空子
集个数有 个;④它的非空真子集有 个。
11、一般地,由所有属于集合A或属于集合B的元素组成的集合,称为集合A与B的并集,
记作 (读作“A并B”),即
。
12、一般地,由所有属于集合A且属于集合B的元素组成的集合,称为集合A与B的交集
记作 (读作“A交B”),即
。
13、一般地,如果一个集合含有所研究问题中涉及的所有元素,那么就称这个集合为全集
通常记作U。对于一个集合A,由全集U中不属于集合A的所有元素组成的集合称为集合
A相对于全集U的补集,简称为集合A的补集,记作,即
∁U
A,即
A= 。
U
14、集合之间的基本关系 ∁
(1)任何一个集合是它本身的子集,即 ;
(2)对于集合A,B,C,如果 ,且 ,那么 。
(3) ; ;
学科网(北京)股份有限公司(4) ; 。
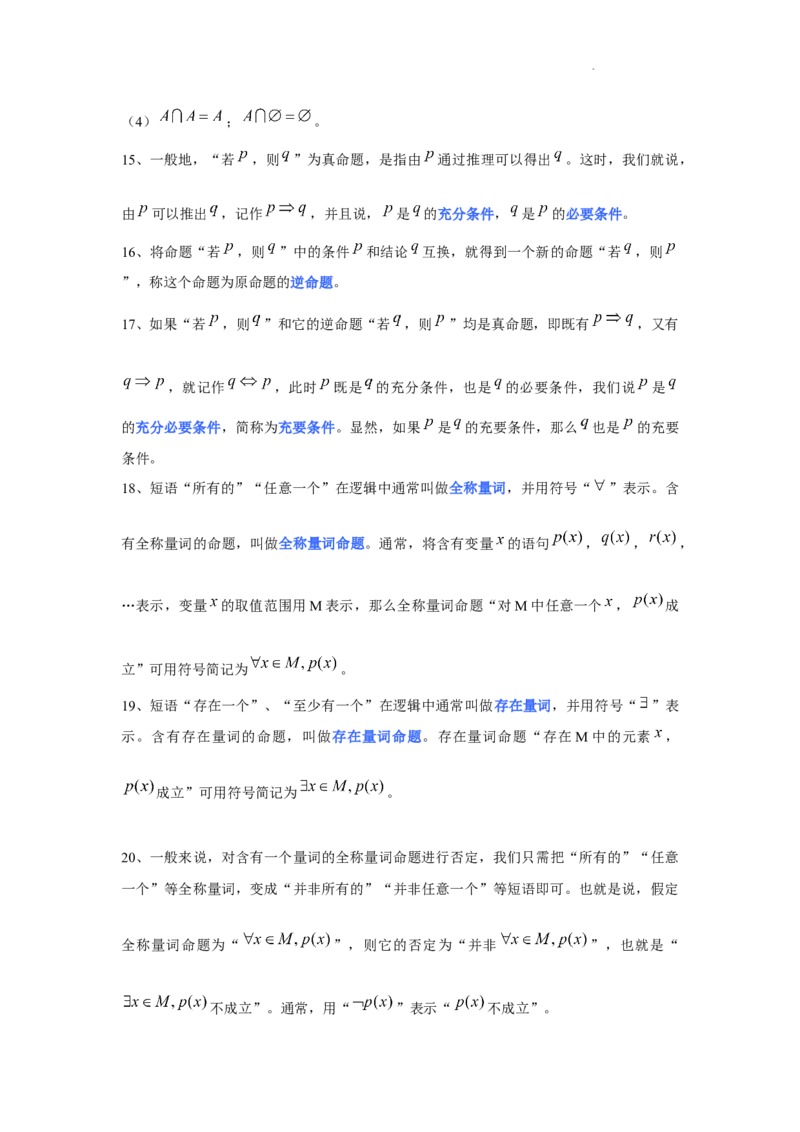
15、一般地,“若 ,则 ”为真命题,是指由 通过推理可以得出 。这时,我们就说,
由 可以推出 ,记作 ,并且说, 是 的充分条件, 是 的必要条件。
16、将命题“若 ,则 ”中的条件 和结论 互换,就得到一个新的命题“若 ,则
”,称这个命题为原命题的逆命题。
17、如果“若 ,则 ”和它的逆命题“若 ,则 ”均是真命题,即既有 ,又有
,就记作 ,此时 既是 的充分条件,也是 的必要条件,我们说 是
的充分必要条件,简称为充要条件。显然,如果 是 的充要条件,那么 也是 的充要
条件。
18、短语“所有的”“任意一个”在逻辑中通常叫做全称量词,并用符号“ ”表示。含
有全称量词的命题,叫做全称量词命题。通常,将含有变量 的语句 , , ,
…表示,变量 的取值范围用M表示,那么全称量词命题“对M中任意一个 , 成
立”可用符号简记为 。
19、短语“存在一个”、“至少有一个”在逻辑中通常叫做存在量词,并用符号“ ”表
示。含有存在量词的命题,叫做存在量词命题。存在量词命题“存在M中的元素 ,
成立”可用符号简记为 。
20、一般来说,对含有一个量词的全称量词命题进行否定,我们只需把“所有的”“任意
一个”等全称量词,变成“并非所有的”“并非任意一个”等短语即可。也就是说,假定
全称量词命题为“ ”,则它的否定为“并非 ”,也就是“
不成立”。通常,用“ ”表示“ 不成立”。
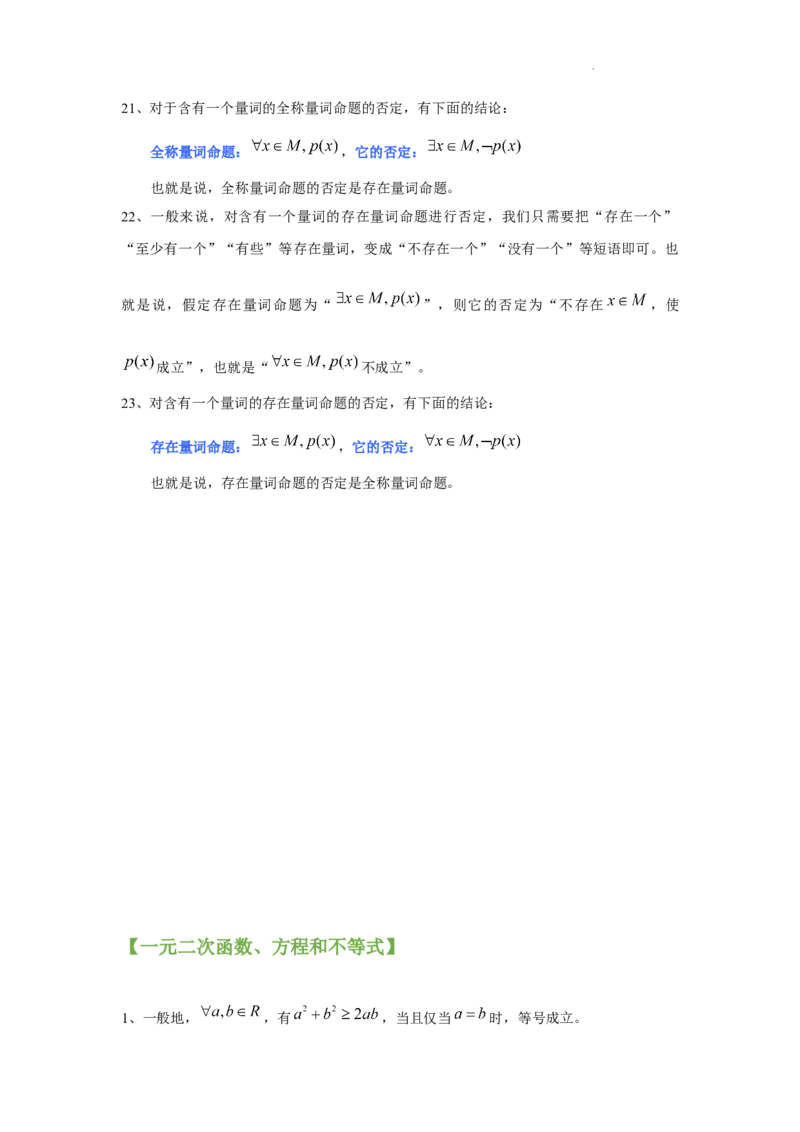
学科网(北京)股份有限公司21、对于含有一个量词的全称量词命题的否定,有下面的结论:
全称量词命题: ,它的否定:
也就是说,全称量词命题的否定是存在量词命题。
22、一般来说,对含有一个量词的存在量词命题进行否定,我们只需要把“存在一个”
“至少有一个”“有些”等存在量词,变成“不存在一个”“没有一个”等短语即可。也
就是说,假定存在量词命题为“ ”,则它的否定为“不存在 ,使
成立”,也就是“ 不成立”。
23、对含有一个量词的存在量词命题的否定,有下面的结论:
存在量词命题: ,它的否定:
也就是说,存在量词命题的否定是全称量词命题。
【一元二次函数、方程和不等式】
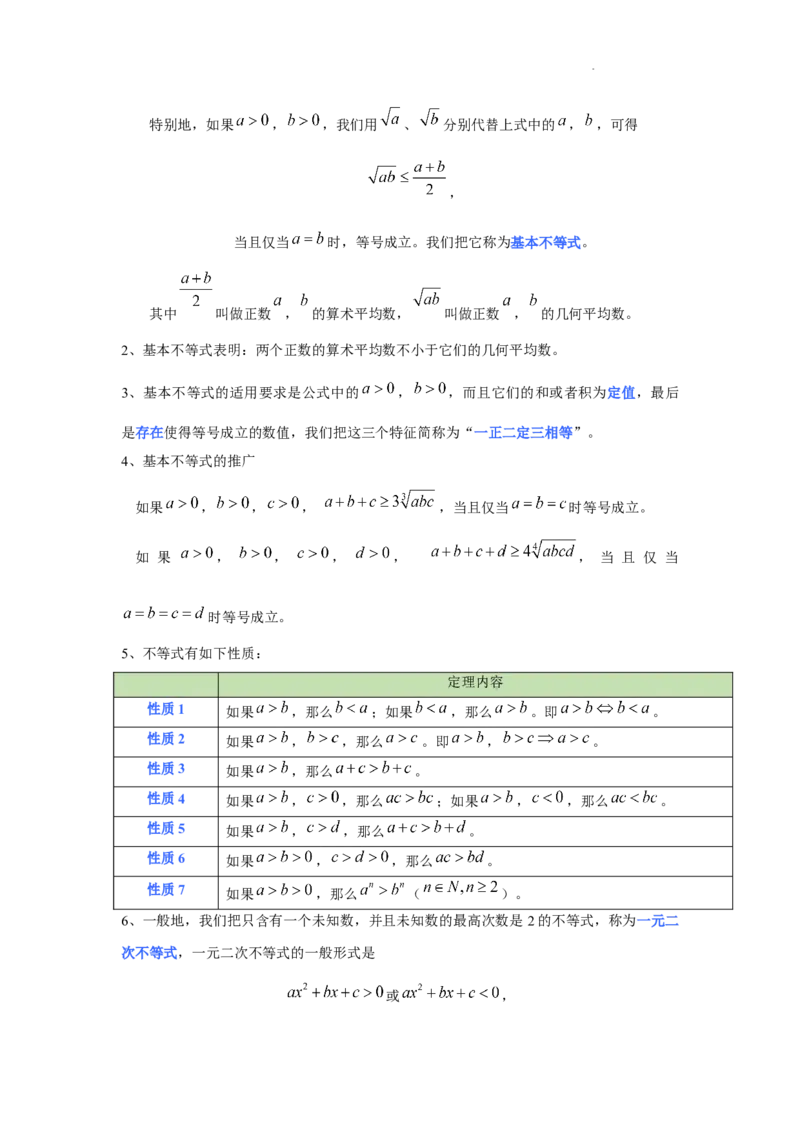
1、一般地, ,有 ,当且仅当 时,等号成立。
学科网(北京)股份有限公司特别地,如果 , ,我们用 、 分别代替上式中的 , ,可得
,
当且仅当 时,等号成立。我们把它称为基本不等式。
其中 叫做正数 , 的算术平均数, 叫做正数 , 的几何平均数。
2、基本不等式表明:两个正数的算术平均数不小于它们的几何平均数。
3、基本不等式的适用要求是公式中的 , ,而且它们的和或者积为定值,最后
是存在使得等号成立的数值,我们把这三个特征简称为“一正二定三相等”。
4、基本不等式的推广
如果 , , , ,当且仅当 时等号成立。
如 果 , , , , , 当 且 仅 当
时等号成立。
5、不等式有如下性质:
定理内容
性质1 如果 ,那么 ;如果 ,那么 。即 。
性质2 如果 , ,那么 。即 , 。
性质3 如果 ,那么 。
性质4 如果 , ,那么 ;如果 , ,那么 。
性质5 如果 , ,那么 。
性质6 如果 , ,那么 。
性质7
如果 ,那么 ( )。
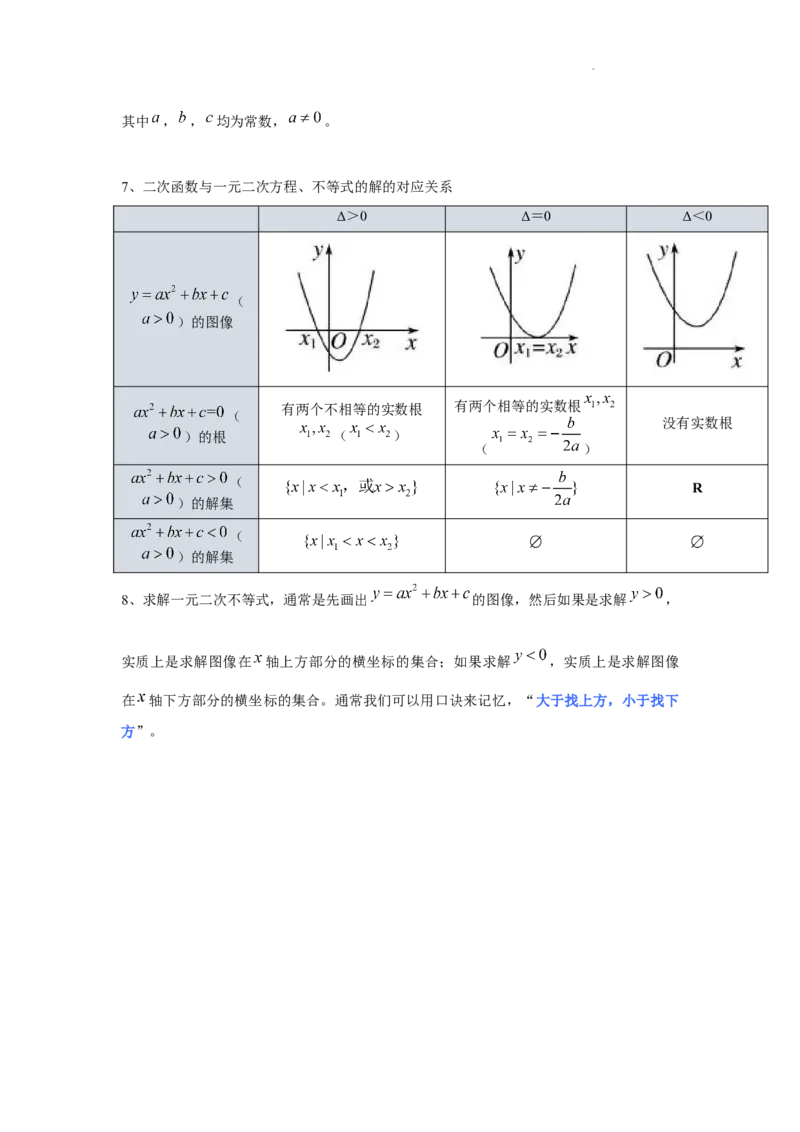
6、一般地,我们把只含有一个未知数,并且未知数的最高次数是 2的不等式,称为一元二
次不等式,一元二次不等式的一般形式是
或 ,
学科网(北京)股份有限公司其中 , , 均为常数, 。
7、二次函数与一元二次方程、不等式的解的对应关系
Δ>0 Δ=0 Δ<0
(
)的图像
有两个不相等的实数根 有两个相等的实数根
(
没有实数根
)的根 ( )
( )
(
R
)的解集
(
)的解集
8、求解一元二次不等式,通常是先画出 的图像,然后如果是求解 ,
实质上是求解图像在 轴上方部分的横坐标的集合;如果求解 ,实质上是求解图像
在 轴下方部分的横坐标的集合。通常我们可以用口诀来记忆,“大于找上方,小于找下
方”。
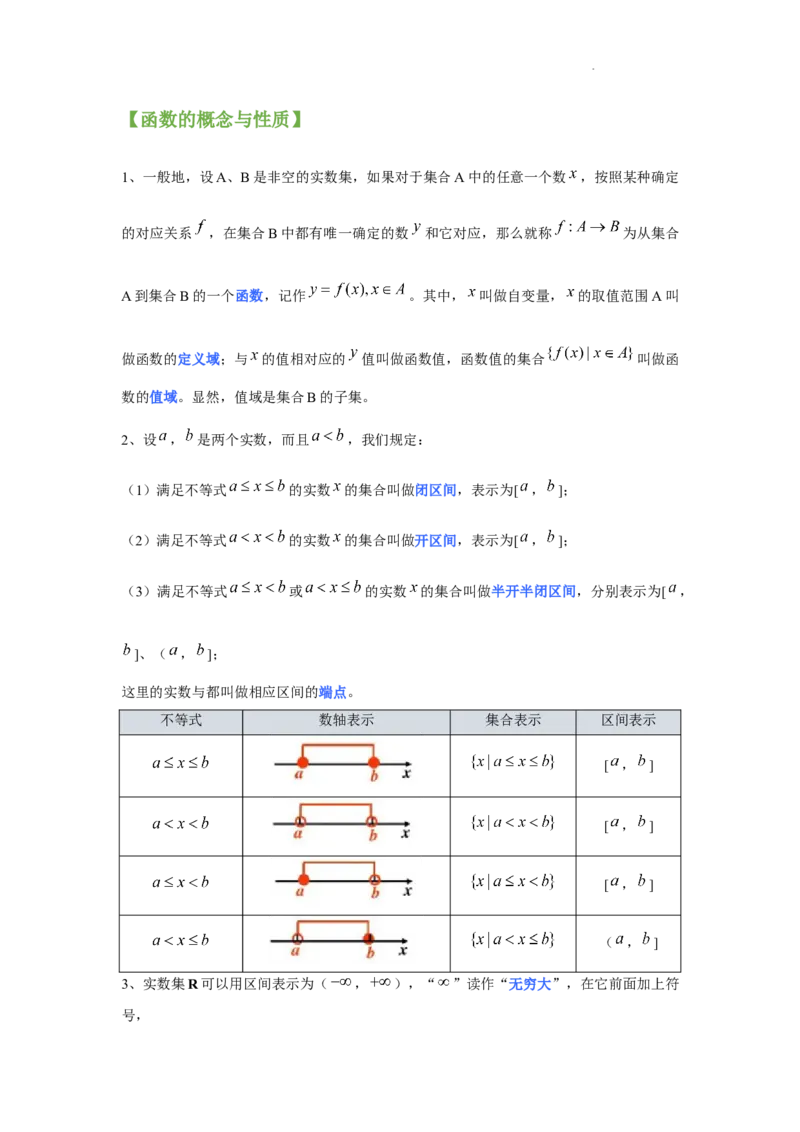
学科网(北京)股份有限公司【函数的概念与性质】
1、一般地,设A、B是非空的实数集,如果对于集合A中的任意一个数 ,按照某种确定
的对应关系 ,在集合B中都有唯一确定的数 和它对应,那么就称 为从集合
A到集合B的一个函数,记作 。其中, 叫做自变量, 的取值范围A叫
做函数的定义域;与 的值相对应的 值叫做函数值,函数值的集合 叫做函
数的值域。显然,值域是集合B的子集。
2、设 , 是两个实数,而且 ,我们规定:
(1)满足不等式 的实数 的集合叫做闭区间,表示为[ , ];
(2)满足不等式 的实数 的集合叫做开区间,表示为[ , ];
(3)满足不等式 或 的实数 的集合叫做半开半闭区间,分别表示为[ ,
]、( , ];
这里的实数与都叫做相应区间的端点。
不等式 数轴表示 集合表示 区间表示
[ , ]
[ , ]
[ , ]
( , ]
3、实数集R可以用区间表示为( , ),“ ”读作“无穷大”,在它前面加上符
号,
学科网(北京)股份有限公司“ ”读作“负无穷大”,“ ”读作“正无穷大”。
我们可以把满足 的实数 的集合,用区间分别表示为[ , )表示,类似地,
, , 可以分别用( , ),( , ],( , )来表示。
4、由函数的定义可知,一个函数的构成要素为:定义域、对应关系和值域。因为值域是由
定义域和对应关系决定的,所以,如果两个函数的定义域相同,并且对应关系完全一致,
即相同的自变量对应的函数值也相同,那么这两个函数是同一个函数。常见的同一函数有:
① 和 ;② 和 。
5、一般地,设函数 的定义域为I,区间D I:
如果 , ,当 时,都有 ,那么就称函数 在区间D
上单调递增。特别地,当函数 在它的定义域上单调递增时,我们就称它是增函数。
如果 , ,当 时,都有 ,那么就称函数 在区间D
上单调递减。特别地,当函数 在它的定义域上单调递减时,我们就称它是减函数。
6、一般地,设函数 的定义域为I,如果存在实数M满足:
(1) ,都有 ;(2) ,使得 。
那么,我们称M是函数 的最大值。
7、一般地,设函数 的定义域为I,如果 ,都有 ,且 ,
那么函数 就叫做偶函数。
8、一般地,设函数 的定义域为I,如果 ,都有 ,且 ,
那么函数 就叫做奇函数。
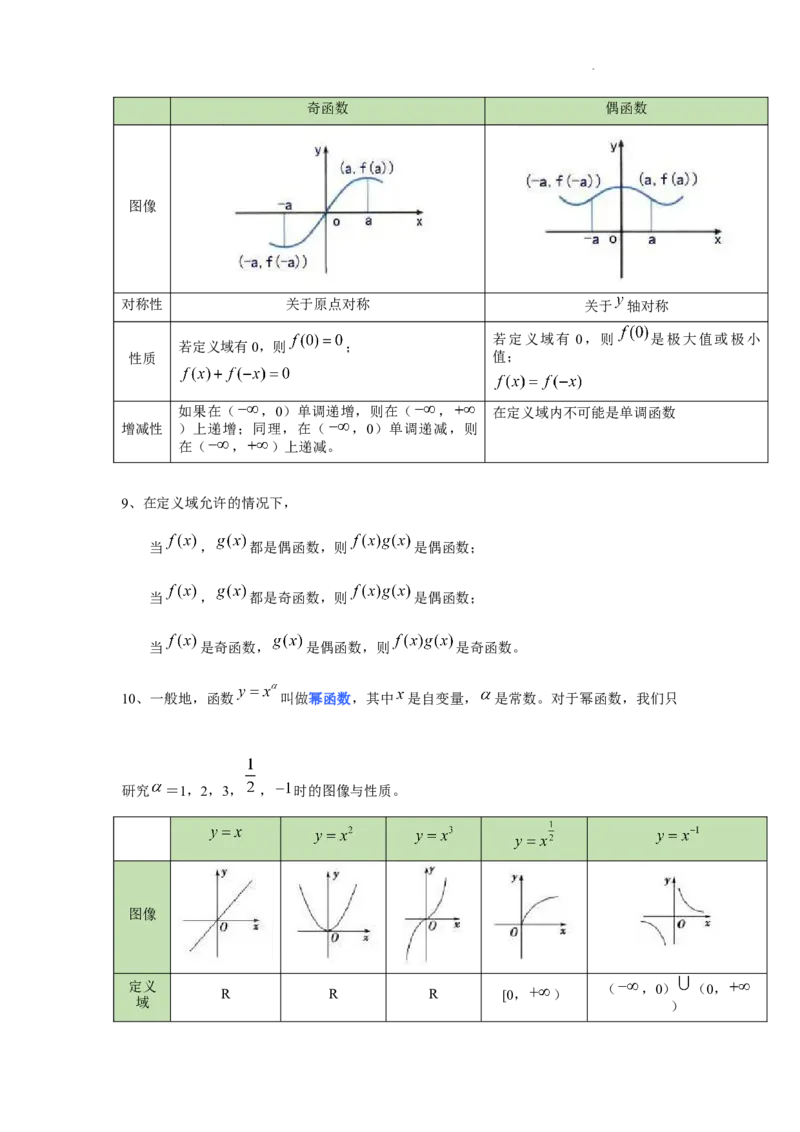
学科网(北京)股份有限公司奇函数 偶函数
图像
对称性 关于原点对称 关于 轴对称
若定义域有 0,则 是极大值或极小
若定义域有0,则 ;
性质 值;
如果在( ,0)单调递增,则在( , 在定义域内不可能是单调函数
增减性 )上递增;同理,在( ,0)单调递减,则
在( , )上递减。
9、在定义域允许的情况下,
当 , 都是偶函数,则 是偶函数;
当 , 都是奇函数,则 是偶函数;
当 是奇函数, 是偶函数,则 是奇函数。
10、一般地,函数 叫做幂函数,其中 是自变量, 是常数。对于幂函数,我们只
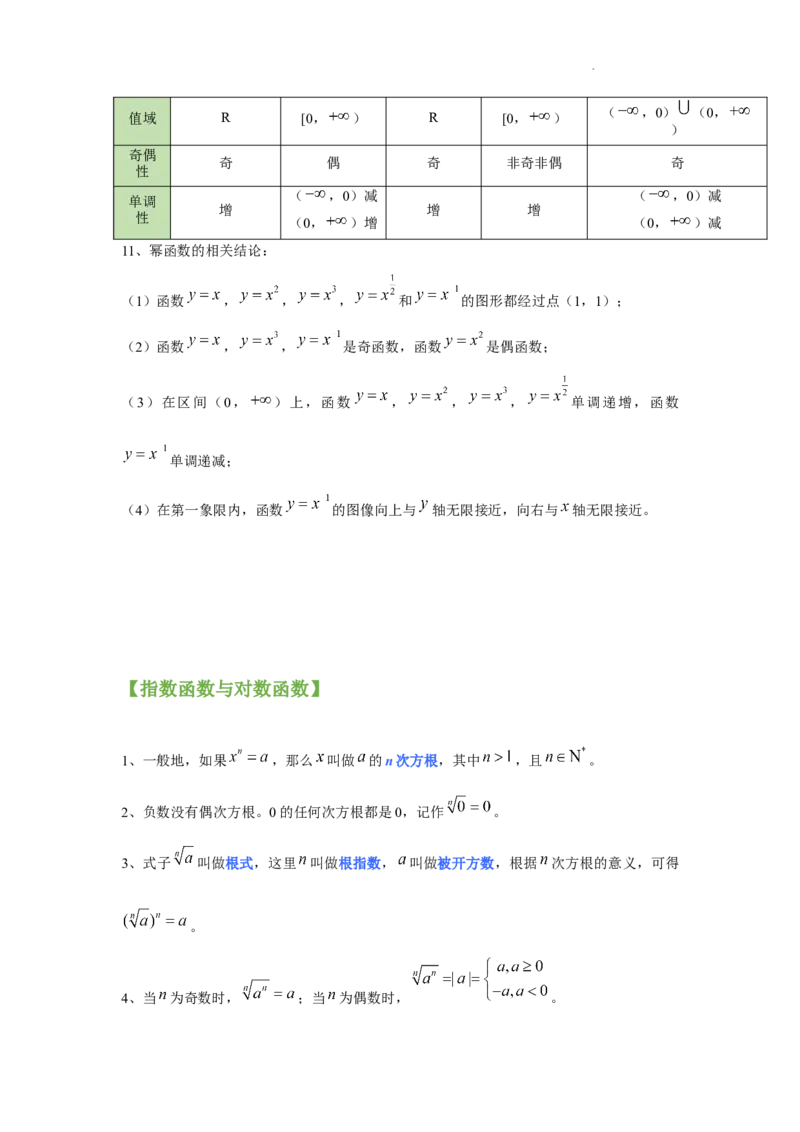
研究 =1,2,3, , 时的图像与性质。
图像
定义 ( ,0) (0,
R R R [0, )
域 )
学科网(北京)股份有限公司( ,0) (0,
值域 R [0, ) R [0, )
)
奇偶
奇 偶 奇 非奇非偶 奇
性
( ,0)减 ( ,0)减
单调
增 增 增
性
(0, )增 (0, )减
11、幂函数的相关结论:
(1)函数 , , , 和 的图形都经过点(1,1);
(2)函数 , , 是奇函数,函数 是偶函数;
(3)在区间(0, )上,函数 , , , 单调递增,函数
单调递减;
(4)在第一象限内,函数 的图像向上与 轴无限接近,向右与 轴无限接近。
【指数函数与对数函数】
1、一般地,如果 ,那么 叫做 的n次方根,其中 ,且 。
2、负数没有偶次方根。0的任何次方根都是0,记作 。
3、式子 叫做根式,这里 叫做根指数, 叫做被开方数,根据 次方根的意义,可得
。
4、当 为奇数时, ;当 为偶数时, 。
学科网(北京)股份有限公司5、我们规定,正数的正分数指数幂的意义是 ( , , , )。
正数的负分数指数幂的意义是 ( , , , )。
6、0的正分数指数幂等于0,0的负分数指数幂没有意义。
7、对于任意实数 、 ,均有下面的运算性质:
(1) ( , , )
(2) ( , , )
(3) ( , , )
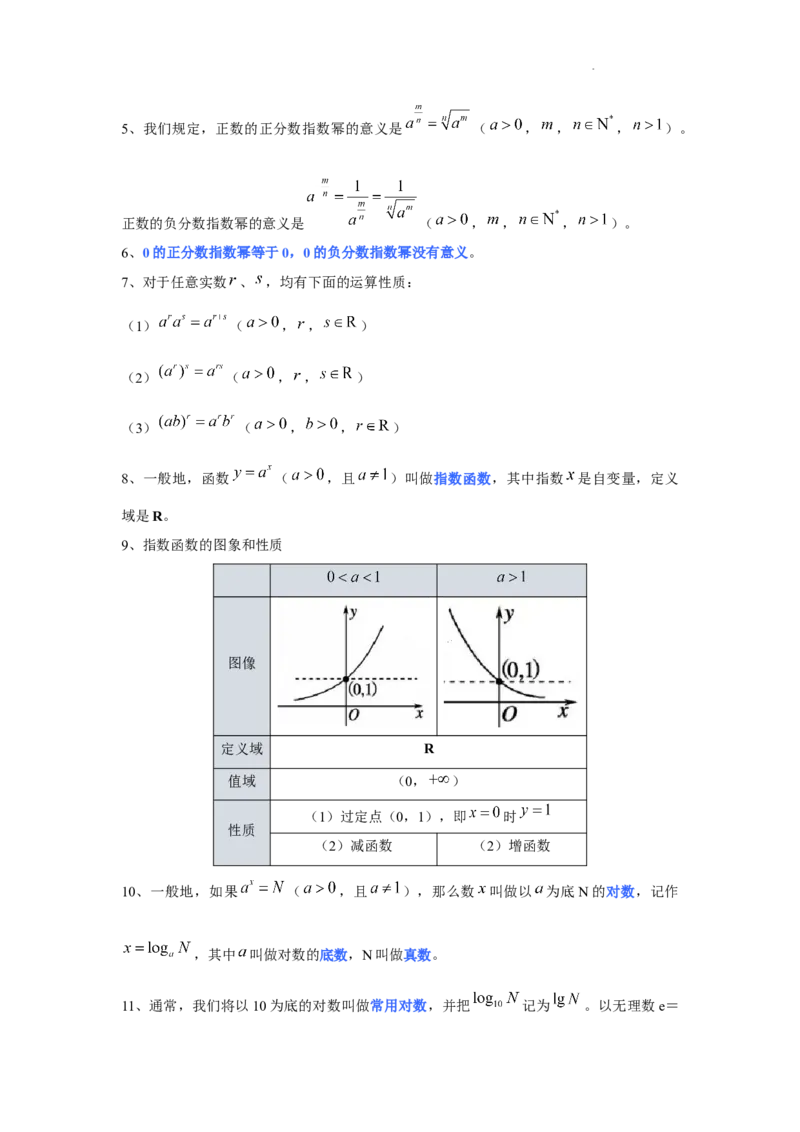
8、一般地,函数 ( ,且 )叫做指数函数,其中指数 是自变量,定义
域是R。
9、指数函数的图象和性质
图像
定义域 R
值域 (0, )
(1)过定点(0,1),即 时
性质
(2)减函数 (2)增函数
10、一般地,如果 ( ,且 ),那么数 叫做以 为底N的对数,记作
,其中 叫做对数的底数,N叫做真数。
11、通常,我们将以10为底的对数叫做常用对数,并把 记为 。以无理数e=
学科网(北京)股份有限公司2.71828…为底的对数称为自然对数,并把 记为 。
12、根据对数的定义,可以得到对数和指数间的关系:
当 ,且 时, 。
13、负数和0没有对数; , 。
14、对数运算性质:如果 ,且 ,M>0,N>0,那么
(1) ;
(2)
(3) ( )
15、对数换底公式: ( ,且 ; ; ,且 )
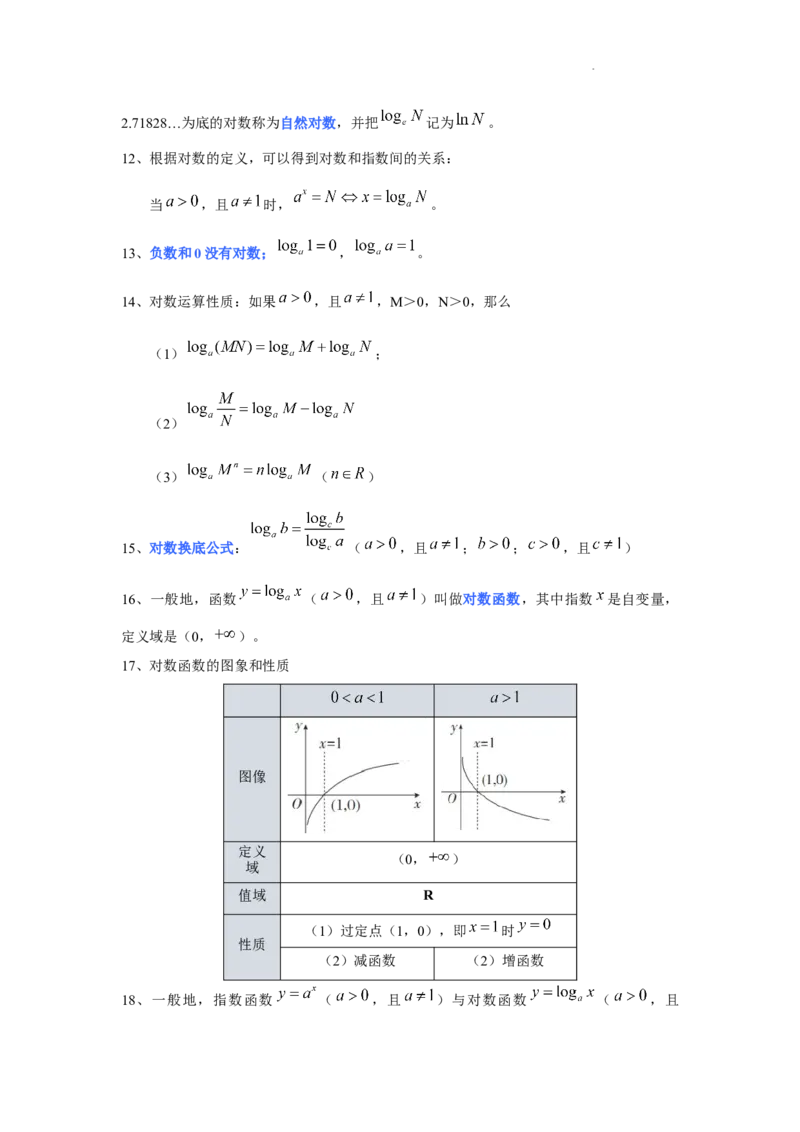
16、一般地,函数 ( ,且 )叫做对数函数,其中指数 是自变量,
定义域是(0, )。
17、对数函数的图象和性质
图像
定义
(0, )
域
值域 R
(1)过定点(1,0),即 时
性质
(2)减函数 (2)增函数
18、一般地,指数函数 ( ,且 )与对数函数 ( ,且
学科网(北京)股份有限公司)互为反函数,它们的定义域和值域互换。
19、对于一般函数 ,我们把使 的实数 叫做函数 的零点。这
样,函数 的零点就是方程 的实数解,也就是函数 的图象与
轴的公共点的横坐标。所以,
方程f ( x )=0有实数解
⇔ 函数y=f ( x )有零点
⇔ 函数y=f ( x )的图像与x轴有公共点
20、函数零点存在定理 一般地,如果函数 在区间[ , ]上的图象是一条连续
不断的曲线,且有 ,那么,函数 在区间( , )内至少有一个
零点,即存在 ( , ),使得 ,这个 也就是方程 的解。
21、对于在区间[ , ]上图象连续不断且 的函数 ,通过不断地把
它的零点所在区间一分为二,使所得区间的两个端点逐步逼近零点,进而得到零点近似值
的方法叫做二分法。
学科网(北京)股份有限公司【三角函数】
1、我们规定,一条射线绕其端点按逆时针方向旋转形成的角叫做正角,按顺时针方向旋转
形成的角叫做负角,如果一条射线没有做任何旋转,就称它形成了一个零角。这样我们就
把角的概念推广到了任意角。
2、一般地,我们有:所有与角α终边相同的角,连同角α在内,可构成一个集合
S={β|β=α+k·360°,k∈Z}
即任一与角α终边相同的角,都可以表示成角α与整数个周角的和。
3、我们规定:长度等于半径长的圆弧所对的圆心角叫做 1弧度的角,弧度单位用符号rad
表示,读作弧度。根据这个规定,在半径为 的圆中,弧长为 的弧所对的圆心角为
rad,那么 。
4、一般地,正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0。
5、扇形的公式:
(1) ;(2) ;(3) 。
其中R是圆的半径, ( )为圆心角, 是扇形的弧长,S是扇形的面积。
6、一般地,任意给定一个角 ,它的终边OP与单位圆交点P的坐标,无论是横坐标
还是纵坐标 ,都是唯一确定的。所以,点P的横坐标 、纵坐标 都是角 的函数。
7、设 是一个任意角, ,它的终边OP与单位圆相交于点P( , ),
我们把点P的纵坐标 叫做 的正弦函数,记作 ,即 ;
学科网(北京)股份有限公司把点P的横坐标 叫做 的余弦函数,记作 ,即 ;
把点P的纵坐标与横坐标的比值 叫做 的正切,记作 ,即 ;
可以看出,当 时, 的终边在 轴上,这时点P的横坐标 等于0,
所以 无意义。除此之外,对于确定的角 , 的值也是唯一确定的。所以
也是以角为自变量,以单位圆上点的纵坐标与横坐标的比值为函数值的
函数,称为正切函数。
8、由三角函数的定义,终边相同的角的同一三角函数的值相等。
9、同一个角α的正弦、余弦的平方和等于1,商等于角α的正切。
即 ,
。
10、诱导公式一~六
公式一 公式二 公式三
公式五 公式六
公式四
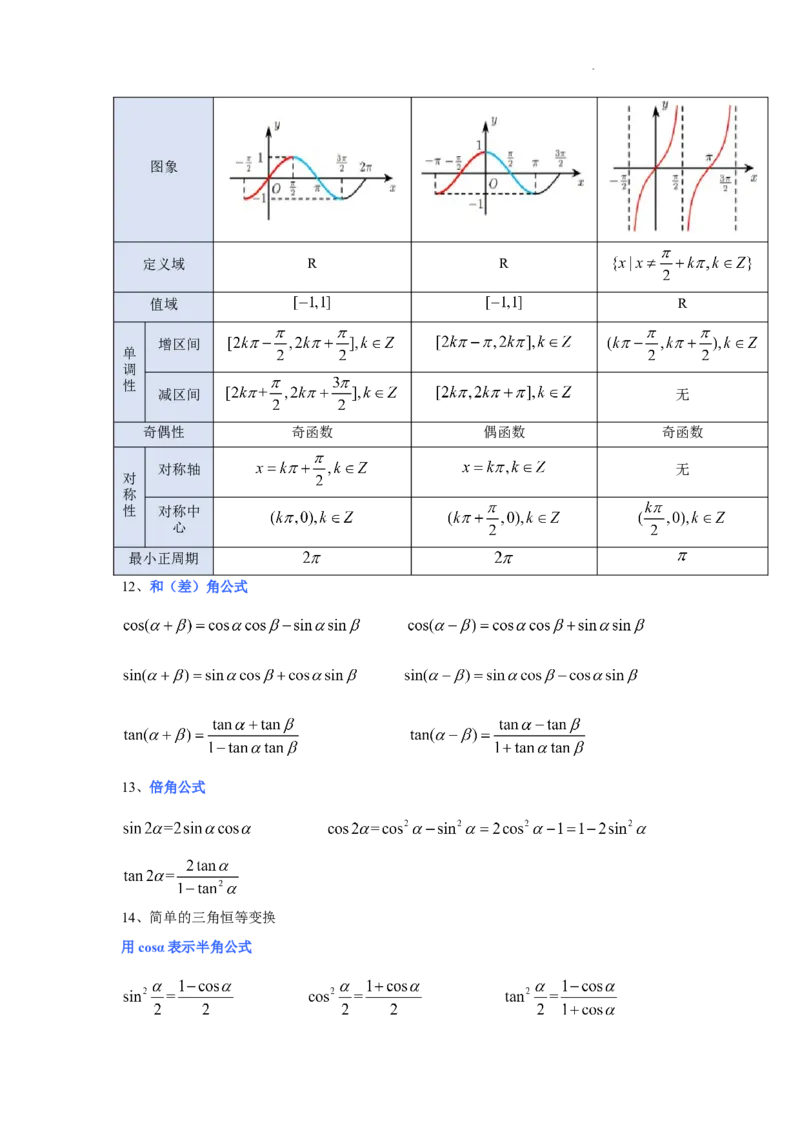
11、三角函数的图象与性质
函数
学科网(北京)股份有限公司图象
定义域 R R
值域 R
增区间
单
调
性
减区间 无
奇偶性 奇函数 偶函数 奇函数
对称轴 无
对
称
性 对称中
心
最小正周期
12、和(差)角公式
13、倍角公式
14、简单的三角恒等变换
用cosα表示半角公式
学科网(北京)股份有限公司积化和差
和差化积
15、辅助角公式
,其中 , 。
16、一般地,把正弦曲线 上的所有点向左(当 >0时)或向右(当 <0时)
平移 个单位长度,就得到函数 的图象。
17、一般地,函数 的周期是 ,把 图象上所有点的横坐
标缩短(当 >1时)或伸长(当0< <1时)到原来的 倍(纵坐标不变),就得到
的图象。
18、一般地,函数 的图象,可以看作是把 图象上所
有点的纵坐标伸长(当A>1时)或缩短(当0<A<1时)到原来的A倍(横坐标不变)
学科网(北京)股份有限公司而得到。从而,函数 的值域是[-A ,A],最大值是A,最小值是-A。
19、在物理学中,把物体受到的力(总是指向平衡位置)正比于它离开平衡位置的距离的
运动称为“简谐运动”。在适当的直角坐标系下,简谐运动可以用函数 ,
表示,其中A>0, >0。A就是这个简谐运动的振幅,它是做简谐运动的物
理离开平衡位置的最大距离;这个简谐运动的周期是T= ,它是做简谐运动的物体往
复运动一次所需要的时间;这个简谐运动的频率由公式 给出,它是做简谐运
动的物体在单位时间内往复运动的次数; 称为相位; =0时的相位 称为初相。
学科网(北京)股份有限公司学科网(北京)股份有限公司