文档内容
高中数学人教A版(2019)选择性必修第一册第二章——
2.2.3直线的一般式方程B
未命名
一、单选题
1.下列有关直线 的说法中正确的是( ).
A.直线 的斜率为 B.直线 的斜率为
C.直线 过定点 D.直线 过定点
2.已知直线 : 的横截距与纵截距相等,则 的值为( )
A.1 B. C. 或2 D.2
3.如果AB>0且BC<0,那么直线Ax+By+C=0不经过第( )象限
A.一 B.二 C.三 D.四
4.“ ”是“直线 与直线 相互垂直”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
5.设 , 为不同的两点,直线 .记 ,
则下列结论中正确的个数是( )
①不论 为何值,点 都不在直线 上;
②若 ,则过 的直线与直线 相交;
③若 ,则直线 经过 的中点.
A.0个 B.1个
C.2个 D.3个.
6.已知 与 是直线 ( 为常数)上两个不同的点,则关于
和 的交点情况是( )
A.无论 , , 如何,总有唯一交点 B.存在 , , 使之有无穷多个交点
试卷第1页,共3页C.无论 , , 如何,总是无交点 D.存在 , , 使之无交点
二、多选题
7.如果 , ,那么直线 经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.下列说法正确的是( )
A.直线 必过定点
B.直线 在 轴上的截距为
C.直线 的倾斜角为60°
D.过点 且垂直于直线 的直线方程为
三、填空题
9.过点 ,且与直线 垂直的直线方程为______.
10.过点 且与直线 垂直的直线方程为______.(用一般式表示)
11.已知圆C: ,点P是圆C上的动点,点 ,当 最大时,
所在直线的方程是______.
12.直线 ,当 变动时,所有直线都通过定点______.
四、解答题
13.已知直线过点 和 两点
(1)求出该直线的直线方程(用点斜式表示)
(2)将(1)中直线方程化成斜截式,一般式以及截距式且写出直线在x轴和y轴上
的截距.
14.已知圆C:(x+2)2+y2=5,直线l:mx﹣y+1+2m=0,m∈R.
试卷第2页,共3页(1)判断直线与圆的位置关系,并说明理由;
(2)若直线 与圆 交于 两点,求弦AB的中点M的轨迹方程.
15.已知直线l分别交梯形 两底 、 于M、N,若l恰平分梯形的面积,求
证:直线l恒过一定点.
16.求满足下列条件的直线方程:
(1)经过 ,且与直线 平行;
(2)在 轴上的截距与在 轴上的截距之差为3,且垂直于过 与 两点的直
线.
试卷第3页,共3页参考答案:
1.D
【分析】讨论 和 两种情况可得.
【详解】直线 可化为 .
当 时,直线 的方程可化为 ,其斜率为 ,过定点 ;
当 时,直线 的方程为 ,其斜率不存在,过点( ,
所以A,B,C不正确,D正确.
故选:D.
2.C
【解析】由直线方程,分别令 , ,然后根据直线横截距与纵截距相等求解.
【详解】由题意得: ,由直线 : ,
令 ,得
令 ,得
因为直线 : 的横截距与纵截距相等,
所以 ,即 ,
解得 或 ,
故选:C
3.C
【分析】根据给定条件,确定直线的斜率和纵截距的取值即可判断作答.
【详解】因AB>0且BC<0,则直线Ax+By+C=0的斜率 ,纵截距
,
所以直线Ax+By+C=0必过第一、二、四象限,不经过第三象限.
故选:C
4.A
【分析】直线 与直线 相互垂直得到 ,再利用充分必要条件的
定义判断得解.
答案第1页,共2页【详解】因为直线 与直线 相互垂直,
所以 ,
所以 .
所以 时,直线 与直线 相互垂直,所以“ ”是“直线
与直线 相互垂直”的充分条件;
当直线 与直线 相互垂直时, 不一定成立,所以“ ”是
“直线 与直线 相互垂直”的非必要条件.
所以“ ”是“直线 与直线 相互垂直”的充分非必要条件.
故选:A
【点睛】方法点睛:充分必要条件的判定,常用的方法有:(1)定义法;(2)集合法;
(3)转化法. 要根据已知条件灵活选择方法求解.
5.C
【分析】①通过分母不为0,确定 ,可以判断①的对错;②③通过对条件
整理变形,利用直线的相关性质判断.
【详解】因为 ,分母不为0,所以 ,所以不论 为何值,
点 都不在直线 上,①正确;
当 时,设 ,( ),则 , 为直线
上的两个点,显然直线 与直线 平行,故过 的直线与直线 不会
相交,②错误;
当 时,设 ,整理得: ,
答案第2页,共2页因为 , ,所以 的中点坐标为 ,故若 ,则直线
经过 的中点.③正确;正确的个数为2个
故选:C
6.A
【分析】根据 在直线 可得 ,从而可得 有唯一交点,从
而可得正确的选项.
【详解】因为 与 是直线 ( 为常数)上两个不同的点,
所以 即 ,
故 既在直线 上,也在直线 上.
因为 与 是两个不同的点,故 、 不重合,
故无论 , , 如何,总有唯一交点 .
故选:A.
7.ABC
【分析】确定直线 在 轴、 轴上截距的正负,数形结合可知直线
所经过的象限.
【详解】直线 在 轴上的截距为 ,在 轴上的截距为 ,
如下图所示:
答案第3页,共2页由图象可知,直线 经过第一、二、三象限.
故选:ABC.
8.ABD
【分析】将方程化为点斜式,即可判断A;令 ,得出在 轴上的截距,进而判断B;
将一般式方程化为斜截式,得出斜率,进而得出倾斜角,从而判断C;由两直线垂直得出
斜率,最后由点斜式得出方程,进而判断D.
【详解】 可化为 ,则直线 必过定
点 ,故A正确;
令 ,则 ,即直线 在 轴上的截距为 ,故B正确;
可化为 ,则该直线的斜率为 ,即倾斜角为 ,故C错误;
设过点 且垂直于直线 的直线的斜率为
因为直线 的斜率为 ,所以 ,解得
则过点 且垂直于直线 的直线的方程为 ,即 ,故
D正确;
故选:ABD
【点睛】本题主要考查了求直线过定点,求直线的倾斜角,由两直线垂直求直线方程,属
于中档题.
9.
【分析】先由垂直关系求出所求直线的斜率,再利用点斜式可求出直线方程
【详解】解:因为所求直线与直线 垂直,
所以所求直线的斜率为 ,
因为所求直线过点 ,
所以所求直线方程为 ,即 ,
故答案为:
【点睛】此题考查两直线的位置关系,考查直线方程的求法,属于基础题
答案第4页,共2页10.
【分析】与直线 垂直的直线方程可设为 ,再将点的坐标代入
运算即可得解.
【详解】解:与直线 垂直的直线方程可设为 ,
又该直线过点 ,则 ,
则 ,
即过点 且与直线 垂直的直线方程为 ,
故答案为: .
11.
【分析】设 ,在 中,由余弦定理,得 ,利用基本不等式
可以找到PM,易得此时 ,可得PM的斜率,从而求得PM的方程.
【详解】设 ,则 ,在 中,由余弦定理,得
,当且仅当 时,等号成立,此时 最大,且 ,
故 ,又 ,所以 ,故 所在直线的方程为
,即 .
故答案为: .
【点睛】本题考查点斜式求直线的方程,涉及到余弦定理、基本不等式、圆等知识,考查
学生的计算能力以及逻辑推理能力,是一道中档题.
12.(3,1)
答案第5页,共2页【解析】将直线方程变形为 ,得到 ,解出 ,即可得到定点坐标.
【详解】由 ,得 ,
对于任意 ,式子恒成立,则有 ,
解出 ,
故答案为:(3,1).
【点睛】本题考查直线过定点问题,直线 一定过两直线
、 的交点.
13.(1) ;(2)答案见解析.
【解析】(1)先求斜率,再利用点斜式写出直线方程;
(2)由 ,得 ,可化为 ,从而可得答案
【详解】解;(1)直线AB的斜率为
故直线AB的点斜式方程为: 或 .
(2)由 ,得 ,可化为 ,
当 时, ,当 时, ,
所以斜截式: ,
一般式: ,
截距式: ,
在x轴上的截距为 ;在y轴上的截距为
答案第6页,共2页14.(1)相交,理由见解析;(2)
【分析】(1)根据直线方程确定直线恒过的定点,结合点与圆的位置关系,即可容易判断
直线与圆的位置关系;
(2)根据 中点在直线 上,结合 ,即可得到点 的轨迹方程,注意讨论斜率
是否存在.
【详解】(1)直线 : ,也即 ,
故直线恒过定点 ,
又 ,故点 在圆 内,
此时直线 一定与圆 相交.
(2)设点 ,
当直线 斜率存在时, ,
又 , ,
即 ,
化简可得: ;
当直线 斜率不存在时,显然中点 的坐标为 也满足上述方程.
故 点的轨迹方程为: .
【点睛】本题考查直线恒过定点的求解,点与圆的位置关系以及动点的轨迹方程,属综合
中档题.
15.证明见解析
【分析】建立直角坐标系,设 , , , .设 , (其
答案第7页,共2页中a、b、c、h为常数, 、 为参变量),根据梯形的面积公式可得
,由恒等式思想可得证.
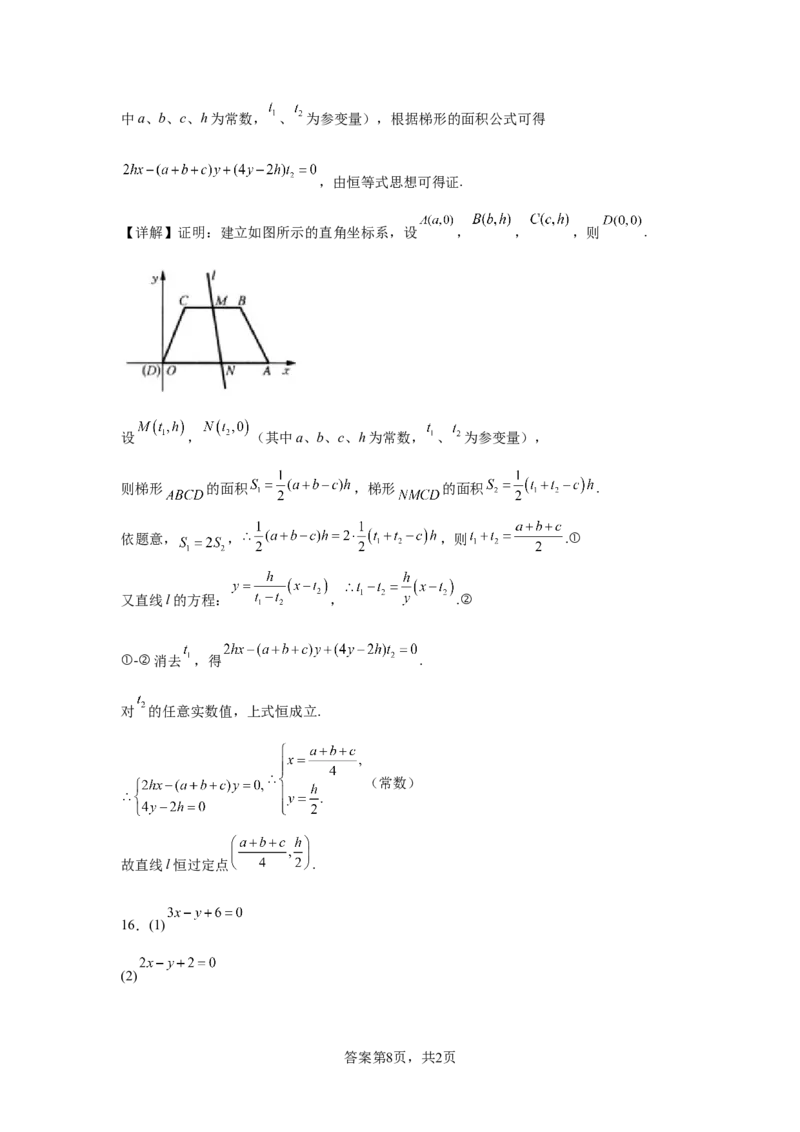
【详解】证明:建立如图所示的直角坐标系,设 , , ,则 .
设 , (其中a、b、c、h为常数, 、 为参变量),
则梯形 的面积 ,梯形 的面积 .
依题意, , ,则 .①
又直线l的方程: , .②
①-②消去 ,得 .
对 的任意实数值,上式恒成立.
(常数)
故直线l恒过定点 .
16.(1)
(2)
答案第8页,共2页【分析】(1)根据题意,设所求直线为 ,进而将A的坐标代入解出b,最后
得到答案;
(2)根据题意先求出直线MN的斜率,进而得到所求直线的斜率,并设为点斜式,然后根
据截距关系求出答案.
(1)
解:设所求直线的方程为 ,将 的坐标代入,得 ,则所求直线的方程为
.
(2)
解:由题意得 ,所求直线的斜率 .
设所求直线的斜截式方程为 .
当 时, ,当 时, ,由 ,得 ,
故所求直线的方程为 .
答案第9页,共2页