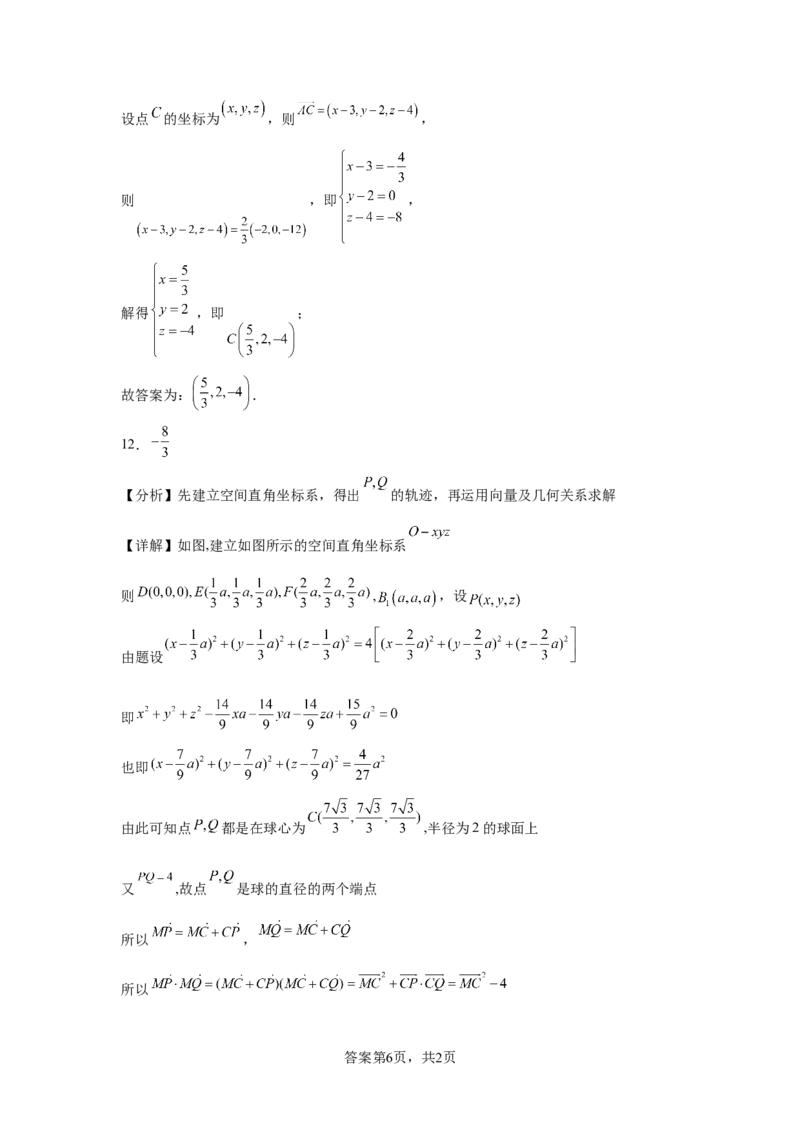文档内容
高中数学人教A版(2019)选择性必修第一册第一章——
1.3空间向量及其运算的坐标表示A
未命名
一、单选题
1.已知 , , 是空间直角坐标系 中 轴、 轴、 轴正方向上的单位向量,
且 , ,则点 的坐标为( )
A. B. C. D.
2.已知 是空间向量的一个基底, 是空间向量的另一个基底,若
向量 在基底 下的坐标为 ,则向量 在基底 下的坐标为
( )
A. B. C. D.
3.已知向量 ,则 ( )
A. B. C. D.0
4.已知 , ,若 与 共线,则实数 ( )
A.-2 B. C. D.2
5.已知 , ,且 与 的夹角为钝角,则 的取值范围是
( ).
A. B. C. D.
6.在空间直角坐标系中,已知长方体 的顶点 , ,
, ,则直线 与平面 之间的距离为( )
试卷第1页,共3页A. B. C. D.
二、多选题
7.已知空间直角坐标系中,点A的坐标为 ,坐标原点为O,且 与
方向相反,则( )
A.x+y+z=0 B.x=3y C.x+z=0 D.4y+z=0
8.已知向量 ,则与 共线的单位向量 ( )
A. B.
C. D.
三、填空题
9.在空间直角坐标系中,点 与点 关于坐标原点对称,则
______.
10.在三棱锥 中,三条侧棱 , , 两两垂直, , ,且
的面积为 ,则 的长为___________.
11.若 、 ,点C在线段AB上,且 ,则点C的坐标是
___________.
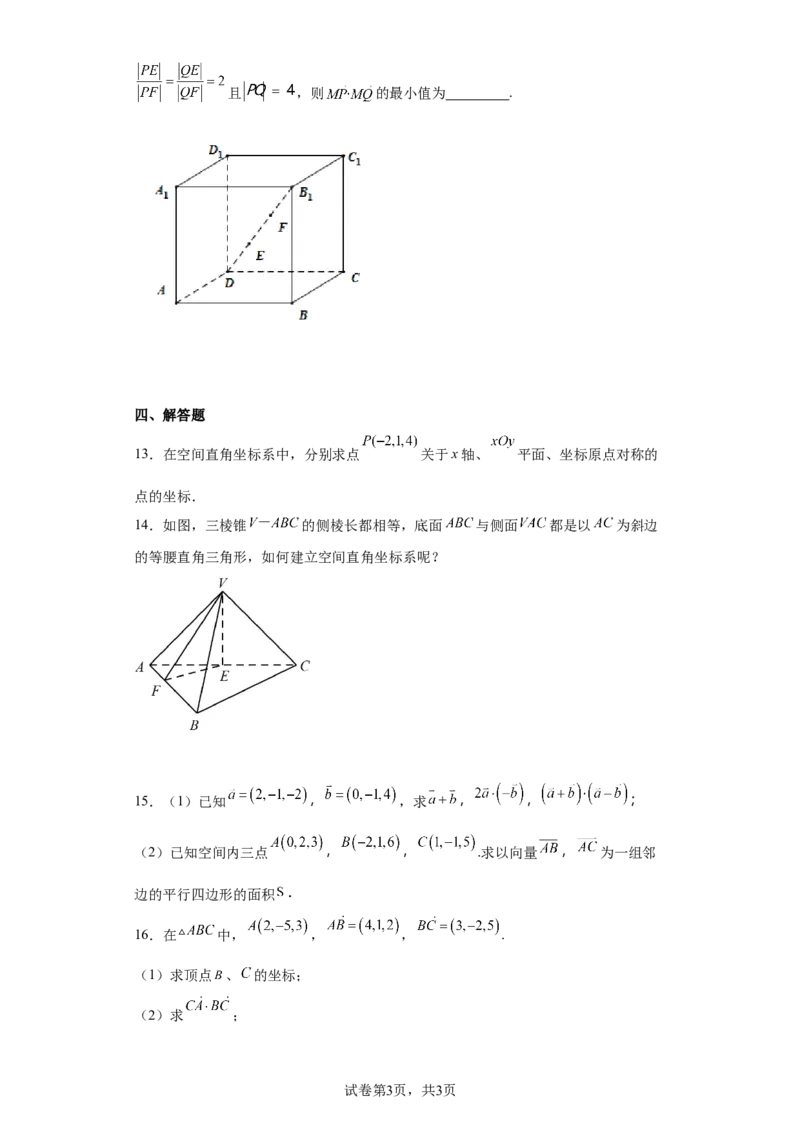
12.如图,在正方体 中, ,点 在线段 上,且
,点 是正方体表面上的一动点,点 是空间两动点,若
试卷第2页,共3页且 ,则 的最小值为 .
四、解答题
13.在空间直角坐标系中,分别求点 关于x轴、 平面、坐标原点对称的
点的坐标.
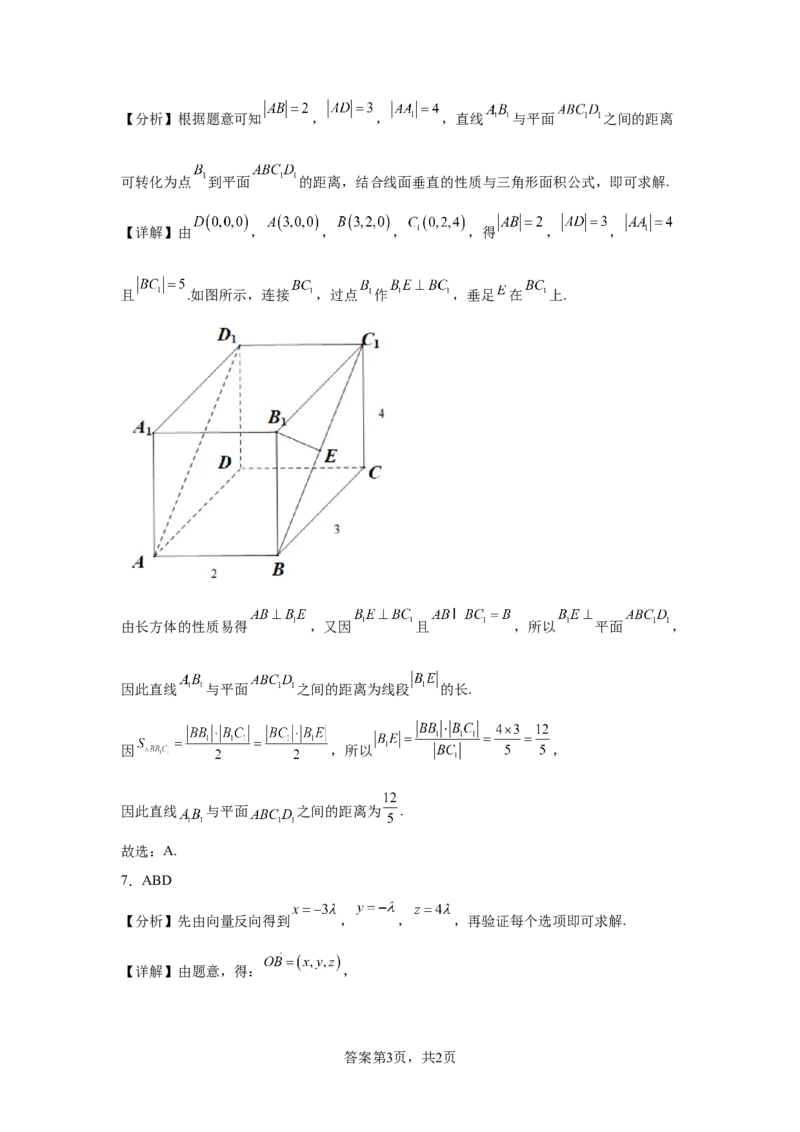
14.如图,三棱锥 的侧棱长都相等,底面 与侧面 都是以 为斜边
的等腰直角三角形,如何建立空间直角坐标系呢?
15.(1)已知 , ,求 , , ;
(2)已知空间内三点 , , .求以向量 , 为一组邻
边的平行四边形的面积 .
16.在 中, , , .
(1)求顶点 、 的坐标;
(2)求 ;
试卷第3页,共3页(3)若点 在 上,且 ,求点 的坐标.
试卷第4页,共3页参考答案:
1.D
【分析】由题设易知 , ,由 ,设 结合空
间向量线性运算的坐标表示求 的坐标.
【详解】由题设知: , ,
∴ ,若 ,则 ,易得 ,
∴ .
故选:D
2.C
【分析】设出 在基底 下的坐标为 ,利用对照系数,得到方程组,求
出结果.
【详解】∵ 在基底 下的坐标为
∴
设 在基底 下的坐标为
则
对照系数,可得:
解得:
∴ 在基底 下的坐标为
故选:C
3.B
【解析】根据空间向量数量积的坐标表示求解.
答案第1页,共2页【详解】 , ,
则 .
故选:B
4.B
【分析】由空间向量线性运算的坐标表示可得 、 ,再
由向量共线的性质即可得解.
【详解】∵ , ,
∴ , .
∵ 与 共线,
∴ ,即 .
故选:B.
【点睛】本题考查了空间向量线性运算及共线的坐标表示,考查了运算求解能力,属于基
础题.
5.A
【分析】夹角为钝角,由 求解,但要排除两向量反向的情形.
【详解】∵ , 的夹角为钝角,∴ ,即 .∴ .
又当 , 的夹角为 时,存在 ,使 ,∴ ,此方程组无解.综上,
.
故选:A.
【点睛】本题考查用数量积确定向量的夹角,当向量 , 的夹角为 时, 也成
立,所以求解此类问题时,要注意检验.
6.A
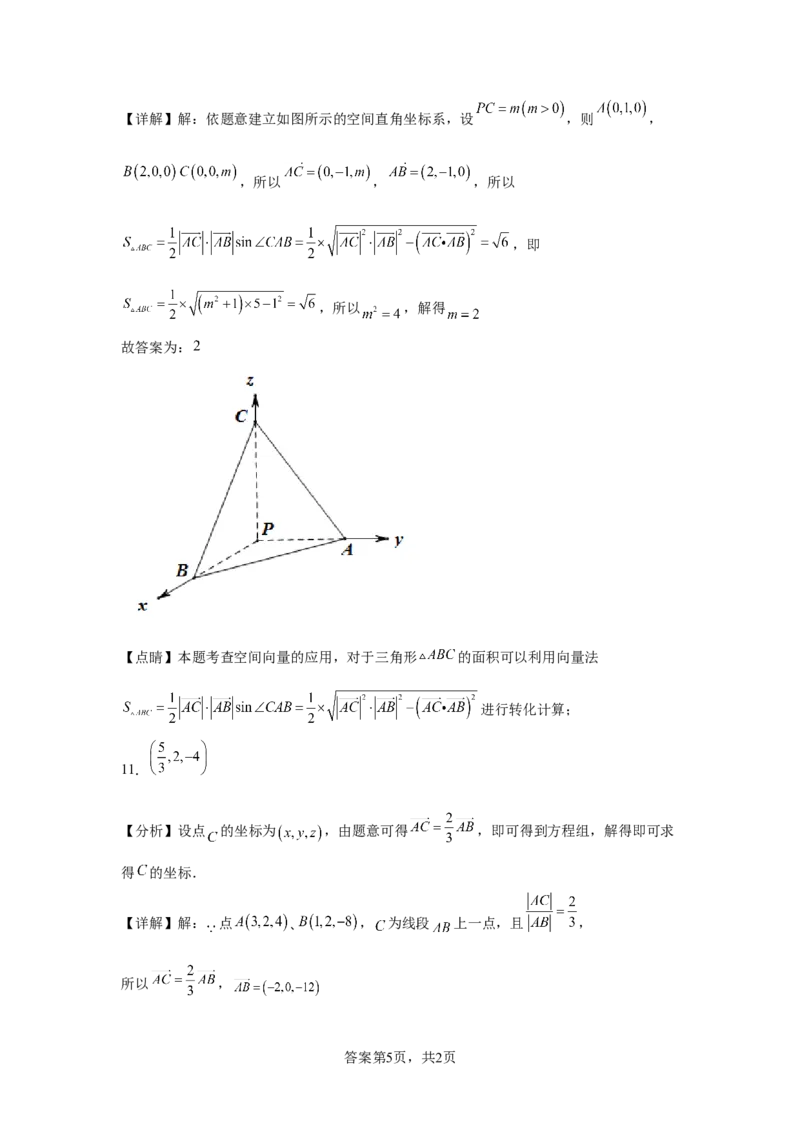
答案第2页,共2页【分析】根据题意可知 , , ,直线 与平面 之间的距离
可转化为点 到平面 的距离,结合线面垂直的性质与三角形面积公式,即可求解.
【详解】由 , , , ,得 , ,
且 .如图所示,连接 ,过点 作 ,垂足 在 上.
由长方体的性质易得 ,又因 且 ,所以 平面 ,
因此直线 与平面 之间的距离为线段 的长.
因 ,所以 ,
因此直线 与平面 之间的距离为 .
故选:A.
7.ABD
【分析】先由向量反向得到 , , ,再验证每个选项即可求解.
【详解】由题意,得: ,
答案第3页,共2页且 ,
其中 ,则 , , ,
则: ,即选项A正确;
,即选项B正确;
,即选项C错误;
,即选项D正确.
故选:ABD.
8.AC
【分析】根据向量数乘的概念,可知单位向量的求法, ,即可求出.
【详解】设与 共线的单位向量为 ,所以 ,因而 ,得到 .
故 ,而 ,所以 或 .
故选:AC.
【点睛】本题主要考查单位向量的求法以及共线向量定理的应用.
9.
【分析】根据对称得到 ,计算得到答案.
【详解】点 与点 关于坐标原点对称,
则 ,故 .
故答案为: .
10.2
【解析】依题意建立空间直角坐标系,设 ,表示出 , ,根据
得到方程,计算可得;
答案第4页,共2页【详解】解:依题意建立如图所示的空间直角坐标系,设 ,则 ,
,所以 , ,所以
,即
,所以 ,解得
故答案为:
【点睛】本题考查空间向量的应用,对于三角形 的面积可以利用向量法
进行转化计算;
11.
【分析】设点 的坐标为 ,由题意可得 ,即可得到方程组,解得即可求
得 的坐标.
【详解】解: 点 、 , 为线段 上一点,且 ,
所以 ,
答案第5页,共2页设点 的坐标为 ,则 ,
则 ,即 ,
解得 ,即 ;
故答案为: .
12.
【分析】先建立空间直角坐标系,得出 的轨迹,再运用向量及几何关系求解
【详解】如图,建立如图所示的空间直角坐标系
则 , ,设
由题设
即
也即
由此可知点 都是在球心为 ,半径为2的球面上
又 ,故点 是球的直径的两个端点
所以 ,
所以
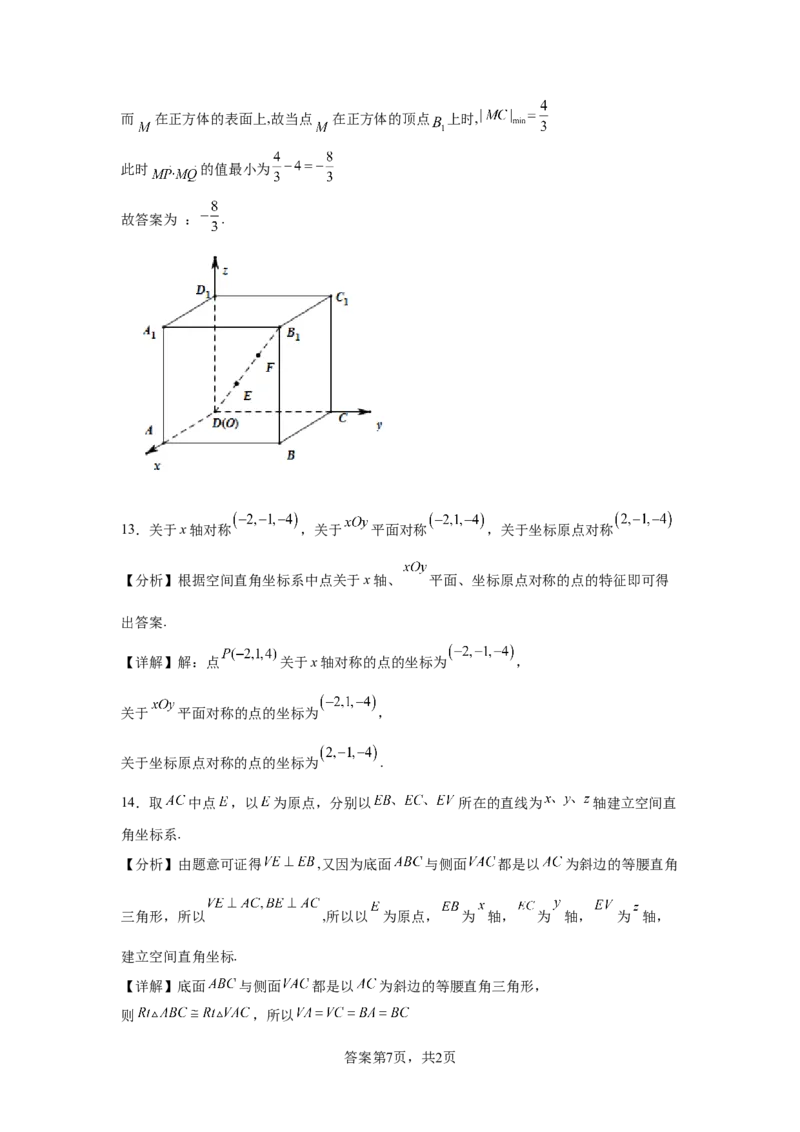
答案第6页,共2页而 在正方体的表面上,故当点 在正方体的顶点 上时,
此时 的值最小为
故答案为 : .
13.关于x轴对称 ,关于 平面对称 ,关于坐标原点对称
【分析】根据空间直角坐标系中点关于x轴、 平面、坐标原点对称的点的特征即可得
出答案.
【详解】解:点 关于x轴对称的点的坐标为 ,
关于 平面对称的点的坐标为 ,
关于坐标原点对称的点的坐标为 .
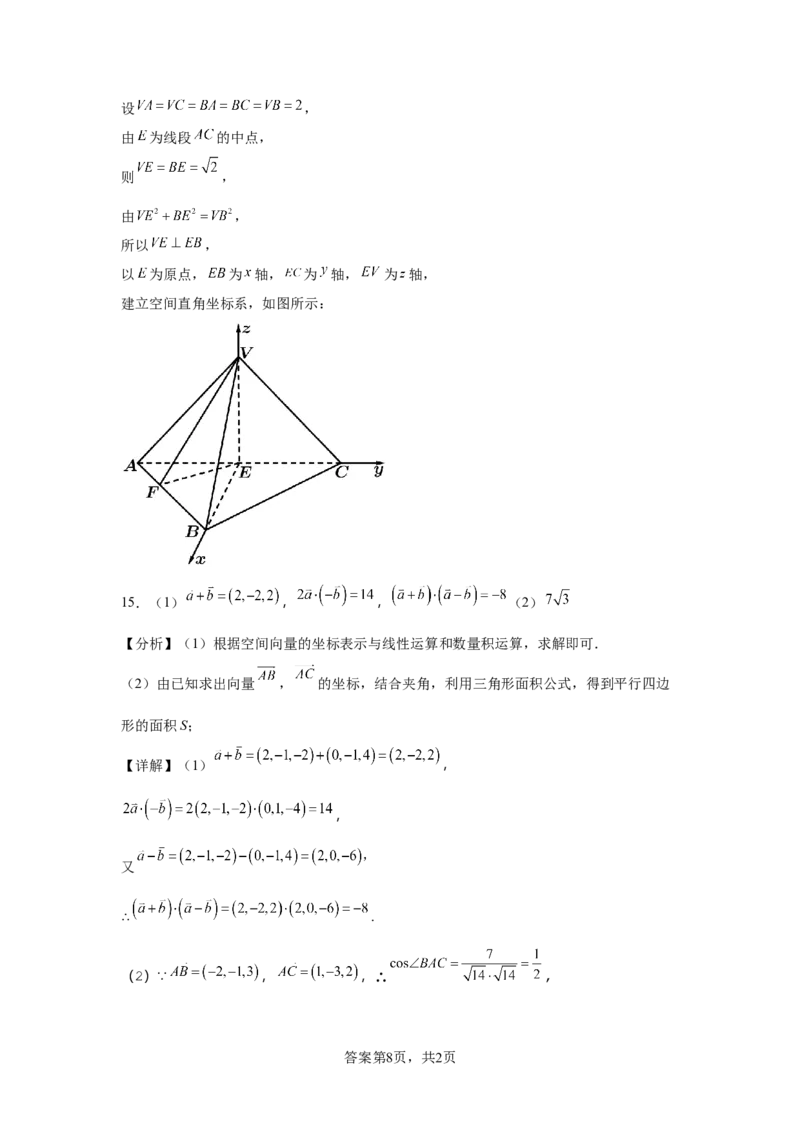
14.取 中点 ,以 为原点,分别以 所在的直线为 轴建立空间直
角坐标系.
【分析】由题意可证得 ,又因为底面 与侧面 都是以 为斜边的等腰直角
三角形,所以 ,所以以 为原点, 为 轴, 为 轴, 为 轴,
建立空间直角坐标.
【详解】底面 与侧面 都是以 为斜边的等腰直角三角形,
则 ,所以
答案第7页,共2页设 ,
由 为线段 的中点,
则 ,
由 ,
所以 ,
以 为原点, 为 轴, 为 轴, 为 轴,
建立空间直角坐标系,如图所示:
15.(1) , , (2)
【分析】(1)根据空间向量的坐标表示与线性运算和数量积运算,求解即可.
(2)由已知求出向量 , 的坐标,结合夹角,利用三角形面积公式,得到平行四边
形的面积S;
【详解】(1) ,
,
又
∴ .
(2)∵ , ,∴ ,
答案第8页,共2页又∵ ,∴ ,∴ .
【点睛】本题考查的知识点是空间向量的坐标表示与线性运算,考查了利用坐标求向量的
模及夹角的问题,属于基础题.
16.(1) , ;(2) ;(3) .
【分析】(1)利用向量的坐标运算可求得点 、 的坐标;
(2)计算出向量 、 的坐标,利用空间向量数量积的坐标运算可求得 的值;
(3)由 可得 ,可求得向量 的坐标,进而可求得点
的坐标.
【详解】(1)设点 为坐标原点, ,
则 .
,则 ;
(2) ,则 ,
又 ,因此, ;
(3)设点 为坐标原点, ,则 ,
则 ,
所以,点 的坐标为 .
【点睛】本题考查空间向量的坐标运算,同时也考查了空间向量数量积的计算,考查计算
能力,属于中等题.
答案第9页,共2页