文档内容
高中数学选择性必修第二册必备知识手册 2024 一轮复习
【数列】
1、一般地,我们把按照确定的顺序排列的一列数称为数列,数列中的每一个数叫做这个数
列的项。其中第1项叫做首项。项数有限的的数列叫做有穷数列,项数无限的数列叫做无
穷数列。
2、数列的一般形式是 , ,…, ,…,简记为 。由于数列 中的每一项
与它的序号 是一一对应的,所以数列 是从正整数集 N*(或它的有限子集{1,
2,…, })到实数集R的函数,其自变量是序号 ,对应的函数值是数列的第 项 ,
记为 。也就是说,当自变量从1开始,按照从小到大的顺序依次取值时,对应的
一系列函数值 , ,…, ,…就是数列 。
3、一般函数的自变量通常是连续变化的,而数列是自变量为离散的数的函数。与函数类似,
我们可以定义数列的单调性。从第2项起,每一项都大于它的前一项的数列叫做递增数列;
从第2项起,每一项都小于它的前一项的数列叫做递减数列。特别地,各项都相等的数列
叫做常数列。
4、如果数列 的第 项 与它的序号 之间的对应关系可以用一个式子来表示,那么
这个式子叫做这个数列的通项公式。通项公式就是数列的函数解析式,根据通项公式可以
写出数列的各项。
5、 或 常常用来表示正负相间的变化规律。
6、如果一个数列的相邻两项或多项之间的关系可以用一个式子来表示,那么这个式子叫做
这个数列的递推公式。知道了首项和递推公式,就能求出数列的每一项。
7、我们把数列 从第1项起到第 项止的各项之和,称为数列 的前 项和,记作
学科网(北京)股份有限公司,即
。
显然 ,而 ,于是我们有
8、一般地,如果一个数列从第2项起,每一项与它的前一项的差都等于同一个常熟,那么
这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字母 表示。
9、由三个数 ,A, 组成的等差数列可以看成是最简单的等差数列。这时,A叫做 与
的等差中项。根据等差数列的定义可以知道, 。
10、首项为 ,公差为 的等差数列 的通项公式为 。
11、由于 ,所以当 时,等差数列 的第 项
是一次函数 当 时的函数值,即 。与此相通,
任给一次函数 ( , 为常数),则 , ,…,
,…构成一个等差数列 ,其首项为 ,公差为 。
12、已知数列 是等差数列, , , , *,且 ,则
。
13、等差数列 的前 项和公式 。把等差数列的通项公式
学科网(北京)股份有限公司代入公式,可得 。
14、等差数列的前 项和公式可以写成 ,所以当 时, 可以
看成二次函数 ( )当 时的函数值。
当 时, 关于 的图像是一条开口向下的抛物线上的一些点;
当 时, 关于 的图像是一条开口向上的抛物线上的一些点。
15、已知 是等差数列 的前 项和,则 是等差数列。
16、已知等差数列 的公差为 ,则 ,这个公式可以从直线的斜率这个角
度来理解。
17、一般地,如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数,那
么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母 表示(显然
)。
18、与等差中项类似,如果在 与 中间插入一个数G,使 ,G, 成等比数列,那么G
叫做 与 的等比中项,此时, 。
19、首项为 ,公比为 的等比数列 的通项公式为
。
20、类似于等差数列与一次函数的关系,由 可知,当 且 时,等比数
学科网(北京)股份有限公司列 的第 项 是指数函数 ( )当 时的函数值。与此相通,
任给指数函数 ( , 为常数, , ,且 ),则 ,
,…, ,…构成一个等比数列 ,其首项为 ,公比为 。
21、等比数列 的前 项和公式 ,因为 ,所以 还可
以写成
。
22、已知等比数列 的公比 ,前 项和为 ,则 , , 成等
比数列,这个数列的公比为 。
23、已知 ,且 ,对于 *,
。
24、一般地,证明一个与正整数 有关的命题,可按下列步骤进行:
(1)(归纳奠基)证明当 ( *)时命题成立;
(2)(归纳递推)以“当 ( *, )时命题成立”为条件,推出“当
时命题也成立”。
只要完成这两个步骤,就可以断定命题对从 开始的所有正整数 都成立,这种证明
方法称为数学归纳法。
25、记 是一个关于正整数 的命题。我们可以把用数学归纳法证明的形式改写如下:
学科网(北京)股份有限公司条件:(1) 为真;(2)若 ( *, )为真,则 也为
真。
结论: 为真。
26、数学归纳法常见的应用公式:
① ;
② ;
③ 。
27、类比等差数列和等比数列的定义、通项公式、常用性质等,发现它们具有如下的对偶
关系:只要将等差数列的一个关系式中的运算“+”改为“×”,“-”改为“÷”,正整数
倍改为正整数指数幂,相应地就可得到等比数列中一个形式相同的关系式,反之也成立。
名称
等差数列 等比数列
定义
通项
公式
常用
若 ( , , , *),则 若 ( , , , *),
性质
则
学科网(北京)股份有限公司【一元函数的导数及其应用】
1、对于函数 ,设自变量 从 变化到 ,相应地,函数值 就从 变
化到 。这时, 的变化量为 , 的变化量为 。我
们把比值 ,即
叫做函数 从 到 的平均变化率。
2、如果当 时,平均变化率 无限趋近于一个确定的值,即 有极限,则称
在 处可导,并把这个确定的值叫做 在 处的导数(也称为
瞬时变化率),记作 或 ,即 。
3、 可以是正值,也可以是负值,但不为0。
4、在曲线 上任取一点P( , )沿着曲线 无限趋近于点 ( ,
学科网(北京)股份有限公司)时,割线 无限趋近于一个确定的位置,这个确定位置的直线 称为曲线
在点 处的切线。容易发现,割线 的斜率可以用平均变化率来表示,当
无限趋近,则它的斜率可以用瞬时变化率来表示。
5、导数的几何意义:在曲线 上任取一点P( , ),在它附近取一点 (
, ),记 ,当点P沿着曲线 无限趋近于点 时,当
时, 无限趋近于函数 在处的导数。因此,函数 在 处的
导数。因此,函数 在 处的导数 就是切线 的斜率 ,即
,这就是导数的几何意义。
6、从求函数 在 处导数的过程可以看到,当 时, 是一个唯一
确定的数。这样,当 变化时, 就是 的函数,我们称它为 的导函数
(简称导数)。 的导函数有时也记作 ,即
。
7、基本初等函数的导数公式表
基本初等函数的导数公式
1、若 ( 为常数),则 ;
2、若 ( 且 ),则 ;
3、若 ,则 ;
学科网(北京)股份有限公司4、若 ,则 ;
5、若 ( 且 ),则 ;
特别地,若 ,则 ;
6、若 ( 且 ),则 ;
特别地,若 ,则 。
8、一般地,对于两个函数 和 的和(或差)的导数,我们有如下法则:
对于两个函数 和 的乘积(或商)的导数,我们有如下法则:
由函数的乘积的导数法则可以得出, ,
也就是说,常数与函数的积的导数,等于常数和函数的导数的积,即 。
9、一般地,对于两个函数 和 ,如果通过中间变量 , 可以表示成
的函数,那么称这个函数为函数 和 的复合函数,记作 。
10、一般地,对于由函数 和 复合而成的函数 ,它的导数与
函数 , 的导数间的关系为 ,即 对 的导数等于 对 的
导数与 对 的导数的乘积。
11、一般地,函数 的单调性与导函数 的正负之间具有如下的关系:
在某个区间( , )上,如果 >0,那么函数在 在区间( , )上单
学科网(北京)股份有限公司调递增;
在某个区间( , )上,如果 <0,那么函数在 在区间( , )上单
调递减。
12、一般情况下,我们可以通过如下步骤判断函数 的单调性:
第1步,确定函数的定义域;
第2步,求出导数 的零点;
第3步,用 的零点将 的定义域划分为若干个区间,列表给出 在各区
间上的正负,由此得出函数 在定义域内的单调性。
13、一般地,函数 在点 的函数值 比它在点 附近其他点的函数值
都小, =0;而且在点 附近的左侧 <0,右侧 >0。
我们把 叫做函数 的极小值点, 叫做函数 的极小值。
14、一般地,函数 在点 的函数值 比它在点 附近其他点的函数值
都大, =0;而且在点 附近的左侧 >0,右侧 <0。
我们把 叫做函数 的极大值点, 叫做函数 的极大值。
15、极小值点、极大值点统称为极值点,极小值和极大值统称为极值。极值反映了函数在
某一点附近的大小情况,刻画了函数的局部性质。
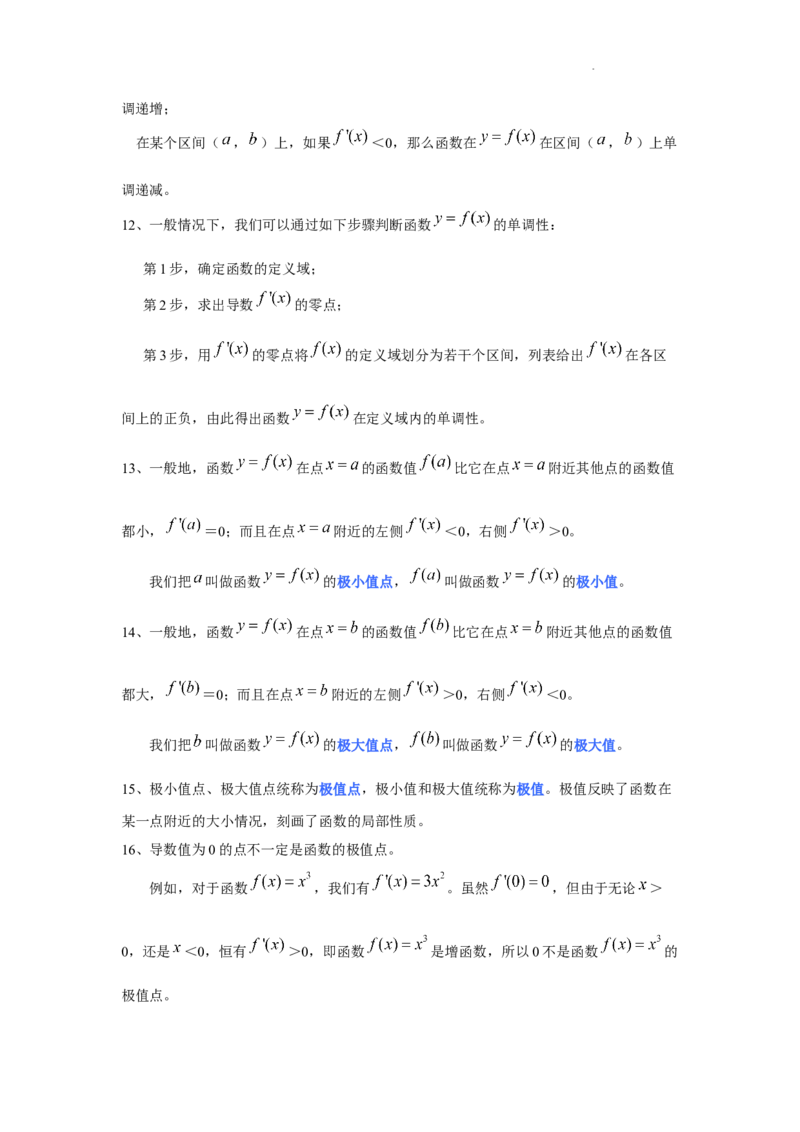
16、导数值为0的点不一定是函数的极值点。
例如,对于函数 ,我们有 。虽然 ,但由于无论 >
0,还是 <0,恒有 >0,即函数 是增函数,所以0不是函数 的
极值点。
学科网(北京)股份有限公司一般地,函数 在一点的导数值为0是函数 在这点取极值的必要条件,
非充分条件。
17、一般地,可按如下方法求函数 的极值:解方程 =0,当 =0时,
(1)如果在 附近的左侧 >0,右侧 <0,那么 是极大值;
(2)如果在 附近的左侧 <0,右侧 >0,那么 是极小值。
18、一般地,如果在区间[ , ]上函数 的图像是一条连续不断的曲线,那么它
必有最大值和最小值。求函数 在区间[ , ]上的最大值与最小值的步骤如下:
(1)求函数 在区间( , )上的极值;
(2)将函数 的各极值与端点处的函数值 , 比较,其中最大的一
个是最大值,最小的一个是最小值。
19、常见不等式的证明:
(1)当 >0时, ; (2)当 >0时, ;
(3)当 时, ; (4)当 >0时, 。
20、函数 的图像可以直观地反映函数 的性质。通常可以按如下步骤画出
的大致图像:
(1)求出函数 的定义域;
(2)求导数 及函数 的零点;
(3)用 的零点将 的定义域划分为若干个区间,列表给出 在各区间
上的正负,并得出 的单调性与极值;
学科网(北京)股份有限公司(4)确定 的图像所经过的一些特殊点,以及图像的变化趋势;
(5)画出 的大致图像。
学科网(北京)股份有限公司