文档内容
高中数学选择性必修第一册必备知识手册 2024 一轮复习
【空间向量与立体几何】
1、O是直线 上一点,在直线 上取非零向量 ,则对于直线 上任意一点P,由数乘向量
的定义及向量共线的充要条件可知,
存在实数 ,使得 。
我们把与向量 平行的非零向量称为直线 的方向向量。这样直线 上任意一点都可以
由直线 上的一点和它的方向向量表示,也就是说,直线可以由其上一点和它的方向向量
确定。
2、如果表示向量 的有向线段 所在的直线OA与直线 平行或重合,那么称向量 平
行于直线 。如果直线OA平行于平面 或在平面 内,那么称向量 平行于平面 。平
行于同一个平面的向量,叫做共面向量。
3、如果两个向量 , 不共线,那么向量 与向量 , 共面的充要条件是存在唯一的有
序实数对( , )使 。
4、向量 向向量 投影,得到与向量 共线的向量 ,则 ,向量
称为向量 在向量 上的投影向量。
5、三垂线定理 在平面的一条直线,如果与这个平面内的一条斜线在这个平面上的射影
垂直,那么它也与这条斜线垂直。
6、定理 如果三个向量 , , 不共面,那么对任意一个空间向量 ,存在唯一的有
学科网(北京)股份有限公司序实数组( , , ),使得 。
由此可知,如果三个向量 , , 不共面,那么所有空间向量组成的集合就是
。这个集合可看作由向量 , , 生成的,我们把{ ,
, }叫做空间的一个基底, , , 都叫做基向量。空间任意三个不共面的向量都可
以构成空间的一个基底。
如果空间的一个基底中的三个基向量两两垂直,且长度都为1,那么这个基底叫做单
位正交基底,常用{ , , }表示。由空间向量基本定理可知,对空间中的任意向量 ,
均可以分解为三个向量 , , ,使 。把一个空间向量分解为三个
两两垂直的向量,叫做把空间向量进行正交分解。
7、在空间选定一点O和一个单位正交基底{ , , },以点O为原点,分别为 , ,
的方向为正方向,以它们的长为单位长度建立三条数轴: 轴、 轴、 轴,它们都叫
做坐标轴,这时我们就建立了一个空间直角坐标系 ,O叫做原点, , , 都叫做
坐标向量,通过每两条坐标轴的平面叫做坐标平面,分别称为 平面, 平面,
平面,它们把空间分成八个部分。画空间直角坐标系 时,一般使 °(或
45°), °。在空间直角坐标系中,让右手拇指指向 轴的正方向,食指指向
轴的正方向,如果中指指向 轴的正方向,则称这个坐标系为右手直角坐标系。
8、在空间直角坐标系 中, , , 为坐标向量,对空间任意一点A,对应一个向
学科网(北京)股份有限公司量 ,且点A的位置由向量 唯一确定,由空间向量基本定理,存在唯一的有序实数
组( , , )使 。在单位正交基底{ , , }下与向量 对应的
有序实数组( , , ),叫做点A在空间直角坐标系中的坐标,记作A( , ,
),其中 叫做A点的横坐标, 叫做A点的纵坐标, 叫做A点的竖坐标。
9、在空间直角坐标系 中,给定向量 ,作 ,由空间向量基本定理,存在唯一
的有序实数组( , , )使 。有序实数组( , , )叫做 在空
间直角坐标系 中的坐标,上式可简记作 。这样,在空间直角坐标系中,
空间中的点坐标和向量都可以用三个有序实数表示。符号( , , )具有双重意义。
10、设 , ,
, ,
,( ) 。
当 时, ( )
; ;
11、空间两点间的距离公式
12、在空间中,我们取一定点O作为基点,那么空间中任意一点P就可以用向量 来表
示。我们把向量 称为点P的位置向量。
学科网(北京)股份有限公司13、给定空间一点A和一条直线 ,则过点A且垂直于直线 的平面是唯一确定的。我们可
以利用点A和直线 的方向向量来确定平面。若直线 ,取直线 的方向向量 ,我们
称向量 为平面 的法向量。给定一个点A和一个向量 ,那么过点A,且以向量为法向
量的平面完全确定,可以表示为
集合{P| =0}。
14、若两条直线平行,则它们的方向向量平行;反之,若两条直线的方向向量平行,则这
两条直线平行。
15、一般地,直线与直线垂直,就是两直线的方向向量垂直;直线与平面垂直,就是直线
的方向向量与平面的法向量平行;平面与平面垂直,就是两平面的法向量垂直。
16、求直线 外一点P到直线 的距离
已知直线 的单位方向向量为 ,A是直线 上的定点,P是直线 外一点,
设 ,则向量 在直线 上的投影向量 ,在Rt APQ中,由勾股
△
定理,得 。
17、求平面 外一点P到平面 的距离
已知平面 的法向量为 ,A是平面 内的定点,P是平面 外一点。
过点P作平面 的垂线 ,交平面 于点Q,则 是直线 的方向向量,且点P到平面
的 距 离 就 是 在 直 线 上 的 投 影 向 量 的 长 度 。 因 此
。
18 、 若 异 面 直 线 , 所 成 的 角 为 , 其 方 向 向 量 分 别 是 , , 则
学科网(北京)股份有限公司。
19、直线AB与平面 相交于点B,设直线AB与平面 所成的角为 ,直线AB的方向向
量为 ,平面 的法向量为 ,则 。
20、平面 与平面 相交,形成四个二面角,我们把这四个二面角中不大于90°的二面角
称为平面α与平面β的夹角。若平面 , 的法向量分别是 和 ,则平面 和平面
的夹角即为向量和的夹角或其补角。设平面 与平面 的夹角为 ,则
。
【直线和圆的方程】
1、当直线 与 轴相交时,我们以 轴为基准, 轴正向与直线 向上的方向之间所称的
角 叫做直线 的倾斜角。当直线 与 轴平行或重合时,我们规定它的倾斜角为0°。因此,
直线的倾斜角 的取值范围为0°≤ <180°。
2、在平面直角坐标系中,每一条直线都有一个确定的倾斜角,而且方向相同的直线,其倾
斜程度相同,倾斜角相等;方向不同的直线,其倾斜程度不同,倾斜角不相等。
3、直线 的倾斜角 与直线 上的两点P ( , ),P ( , )( )的坐标
1 2
有如下关系:
。
学科网(北京)股份有限公司4、我们把一条直线的倾斜角 的正切值叫做这条直线的斜率,斜率常用小写字母 表示,
即 。倾斜角是 90°的直线没有斜率,倾斜角不是90°的直线都有斜率。
5、由于正切函数的单调性,倾斜角不同的直线,其斜率也不同。因此,我们可以用斜率表
示倾斜角不等于90°的直线相对于 轴的倾斜程度,进而表示直线的方向。如果直线经过两
点P( , ),P( , )( ),那么斜率公式: 。
1 2
6、讨论两条存在斜率的直线,若 ,则 。反之,若 ,则 。
7、设两条直线 , 的斜率分别为 , ,则直线 , 的方向向量分别是 ,
,于是 ,即 ,也就是说,
。
8、当直线 或 的倾斜角为90°时,若 ,则另一条直线的倾斜角为0°;反之亦然。
9、一般地,我们把方程 称为过点 ( , ),斜率为 的直线 的
方向,它由直线上一个定点( , )及该直线的斜率 确定,我们把它叫做直线的点斜
式方程,简称点斜式。
10、当直线 的倾斜角为0°时,直线 的方程是 ;当直线 的倾斜角为90°时,直线
的方程是 。
11、我们把方程 叫做直线的斜截式方程,简称斜截式。其中 和 均有明显的
几何意义: 是直线的斜率, 是直线在 轴上的截距。值得强调的是,截距 是直线 与
学科网(北京)股份有限公司轴的交点的纵坐标。
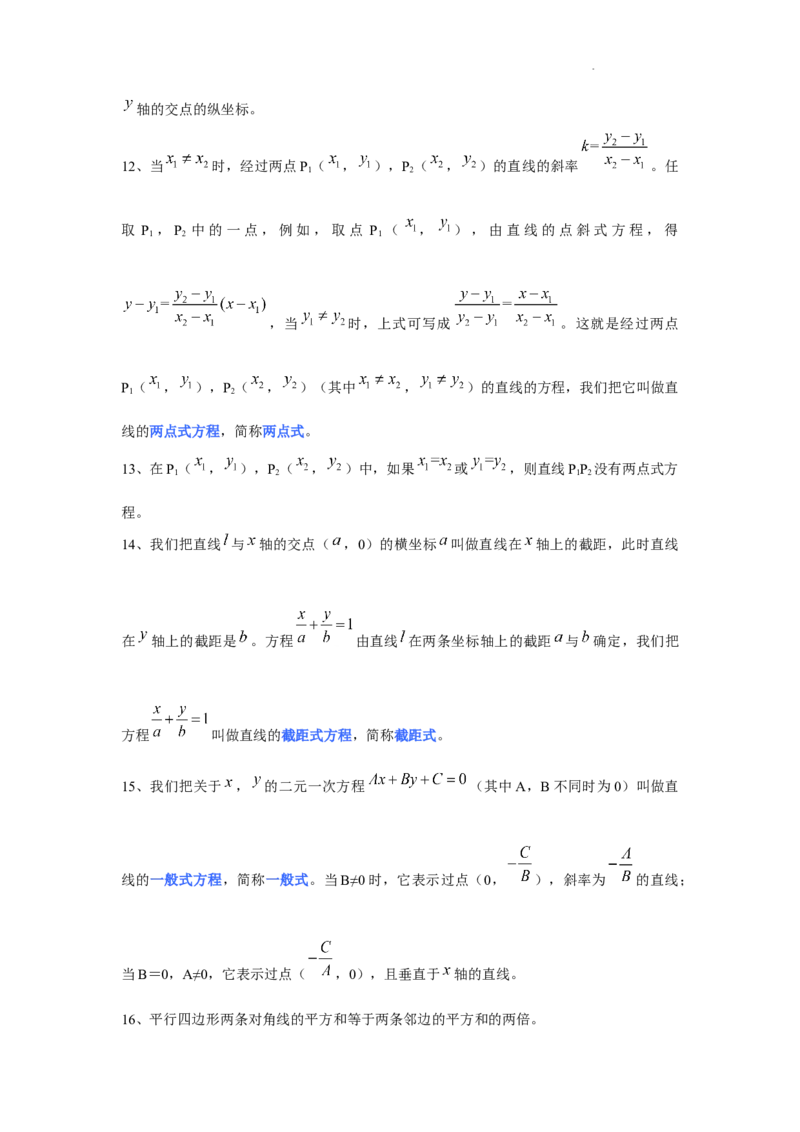
12、当 时,经过两点P ( , ),P ( , )的直线的斜率 。任
1 2
取 P ,P 中的一点,例如,取点 P ( , ),由直线的点斜式方程,得
1 2 1
,当 时,上式可写成 。这就是经过两点
P ( , ),P ( , )(其中 , )的直线的方程,我们把它叫做直
1 2
线的两点式方程,简称两点式。
13、在P( , ),P( , )中,如果 或 ,则直线PP 没有两点式方
1 2 1 2
程。
14、我们把直线 与 轴的交点( ,0)的横坐标 叫做直线在 轴上的截距,此时直线
在 轴上的截距是 。方程 由直线 在两条坐标轴上的截距 与 确定,我们把
方程 叫做直线的截距式方程,简称截距式。
15、我们把关于 , 的二元一次方程 (其中A,B不同时为0)叫做直
线的一般式方程,简称一般式。当B≠0时,它表示过点(0, ),斜率为 的直线;
当B=0,A≠0,它表示过点( ,0),且垂直于 轴的直线。
16、平行四边形两条对角线的平方和等于两条邻边的平方和的两倍。
学科网(北京)股份有限公司17、点P( , )到直线 : 的距离
。
18、两条平行直线 与 间的距离为
。
19、已知AO是△ABC边BC的中线, 。
20、我们把 称为圆心为A( , ),半径为 的圆的标准方程。
21、△ABC的外接圆的圆心是△ABC的外心,即△ABC三边垂直平分线的交点。
22、一般地,圆的标准方程 可以变形为 ,
将变形后的方程左边配方,并把常数项移到右边,得 ,
①当 时,它是以( , )为圆心, 为半径的圆;
②当 时,它表示一个点( , );
③当 时,它不表示任何图形。
因此,当 时, 表示一个圆,我们把它叫做圆
的一般方程。
23、在平面直角坐标系中,如果点P的坐标( , )满足 , 其中 为参
数,则点P的轨迹是圆心为( , ),半径为 的圆。
学科网(北京)股份有限公司【圆锥曲线的方程】
1、我们把平面内与两个定点F ,F 的距离的和等于常数(大于|FF|)的点的轨迹叫做椭
1 2 1 2
圆;这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距,焦距的一半称为半焦
距。
2、椭圆的标准方程与性质
3、我们把椭圆的焦距与长轴长的比称为椭圆的离心率,用 表示,即 。 越接近
1,椭圆越扁平;反之, 越接近0,椭圆越接近于圆。
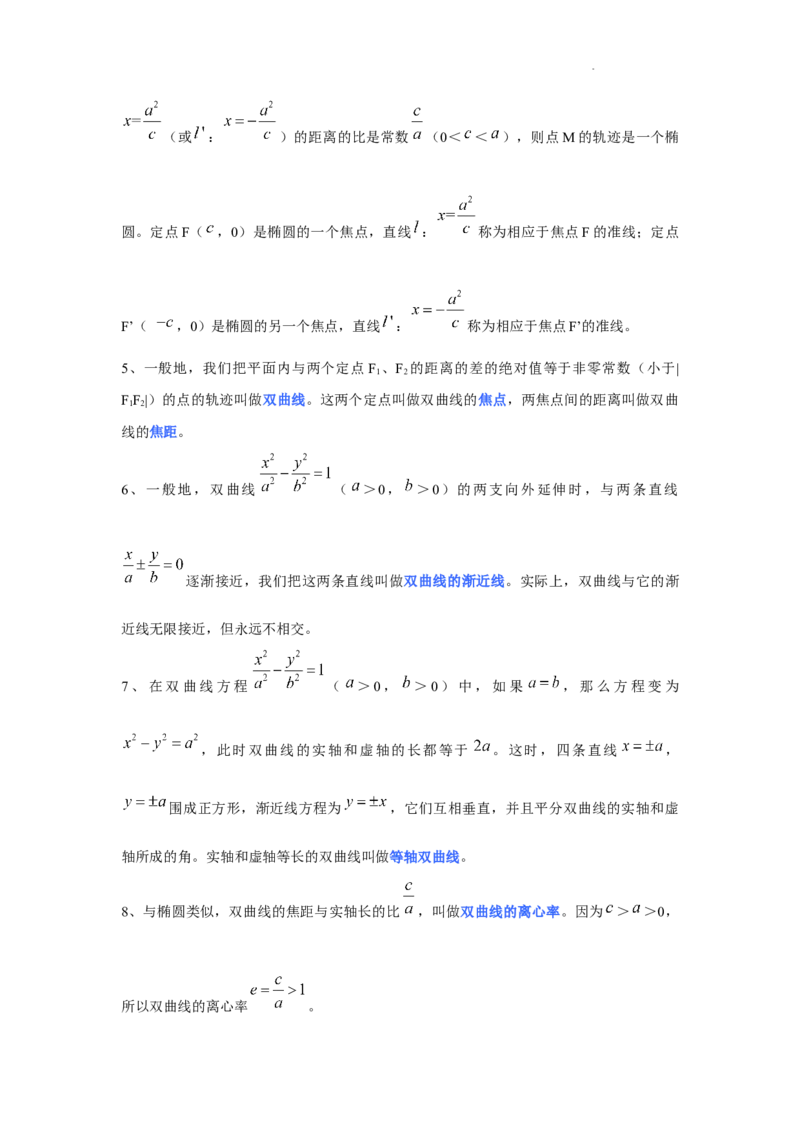
4、若点M( , )与定点F( ,0)(或F’( ,0))的距离和它到定直线 :
学科网(北京)股份有限公司(或 : )的距离的比是常数 (0< < ),则点M的轨迹是一个椭
圆。定点F( ,0)是椭圆的一个焦点,直线 : 称为相应于焦点F的准线;定点
F’( ,0)是椭圆的另一个焦点,直线 : 称为相应于焦点F’的准线。
5、一般地,我们把平面内与两个定点F 、F 的距离的差的绝对值等于非零常数(小于|
1 2
FF|)的点的轨迹叫做双曲线。这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲
1 2
线的焦距。
6、一般地,双曲线 ( >0, >0)的两支向外延伸时,与两条直线
逐渐接近,我们把这两条直线叫做双曲线的渐近线。实际上,双曲线与它的渐
近线无限接近,但永远不相交。
7、在双曲线方程 ( >0, >0)中,如果 ,那么方程变为
,此时双曲线的实轴和虚轴的长都等于 。这时,四条直线 ,
围成正方形,渐近线方程为 ,它们互相垂直,并且平分双曲线的实轴和虚
轴所成的角。实轴和虚轴等长的双曲线叫做等轴双曲线。
8、与椭圆类似,双曲线的焦距与实轴长的比 ,叫做双曲线的离心率。因为 > >0,
所以双曲线的离心率 。
学科网(北京)股份有限公司9、如果动点M到定点F的距离与M到定直线 (不过点F)的距离之比为 ,当0< <1
时,点M的轨迹为椭圆;当 >1时,点M的轨迹为双曲线。当 =1时,点M的轨迹为
抛物线。
10、我们把平面内与一个定点F和一条定直线 ( 不经过点F)的距离相等的点的轨迹叫
做抛物线。点F叫做抛物线的焦点,直线 叫做抛物线的准线。
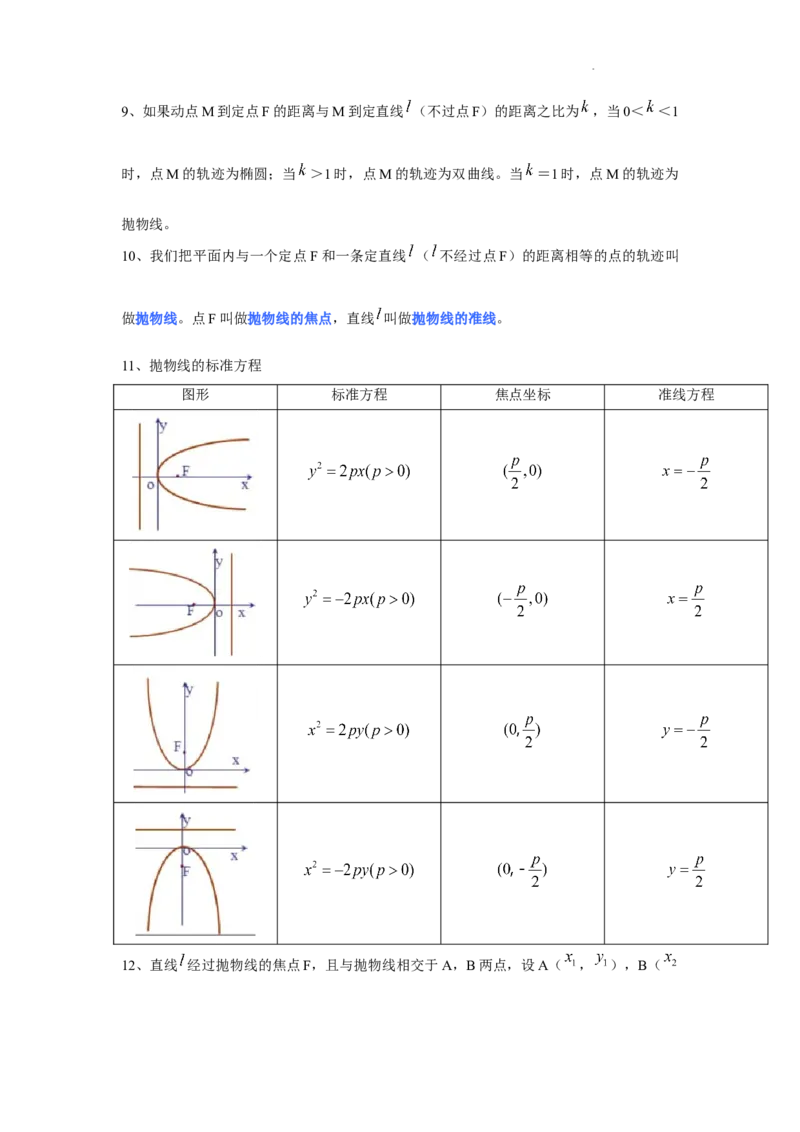
11、抛物线的标准方程
图形 标准方程 焦点坐标 准线方程
12、直线 经过抛物线的焦点F,且与抛物线相交于A,B两点,设A( , ),B(
学科网(北京)股份有限公司, ),线段AB的长为 。
13、经过抛物线焦点F的直线交抛物线于A,B两点,经过点A和抛物线顶点的直线交抛
物线的准线于点D,则直线DB平行于抛物线的对称轴。
学科网(北京)股份有限公司