文档内容
高二(下)期末测试卷(A 卷 基础巩固)
理科数学
考试时间:120分钟 满分:150分
一、选择题:本大题共8小题,每个小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要
求的.
1.(2021·黑龙江大庆市·铁人中学高三一模(文))复数 (其中 为虚数单位),则 的实部和
虚部的和为( )
A.2 B. C. D.
2.(2021·云南昆明一中高三其他模拟(文))设集合 , ,则 (
)
A. B. C. D.
3.(2021·武威第六中学高三其他模拟(文))2021年开始,某省将试行“ ”的普通高考新模式,
即除物理语文、数学、外语3门必选科目外,考生再从物理、历史中选1门,从化学、生物、地理、政治
中选2门作为选考科目.为了帮助政治学生合理选科,某中学将高一每个学生的六门科目综合成绩按比例
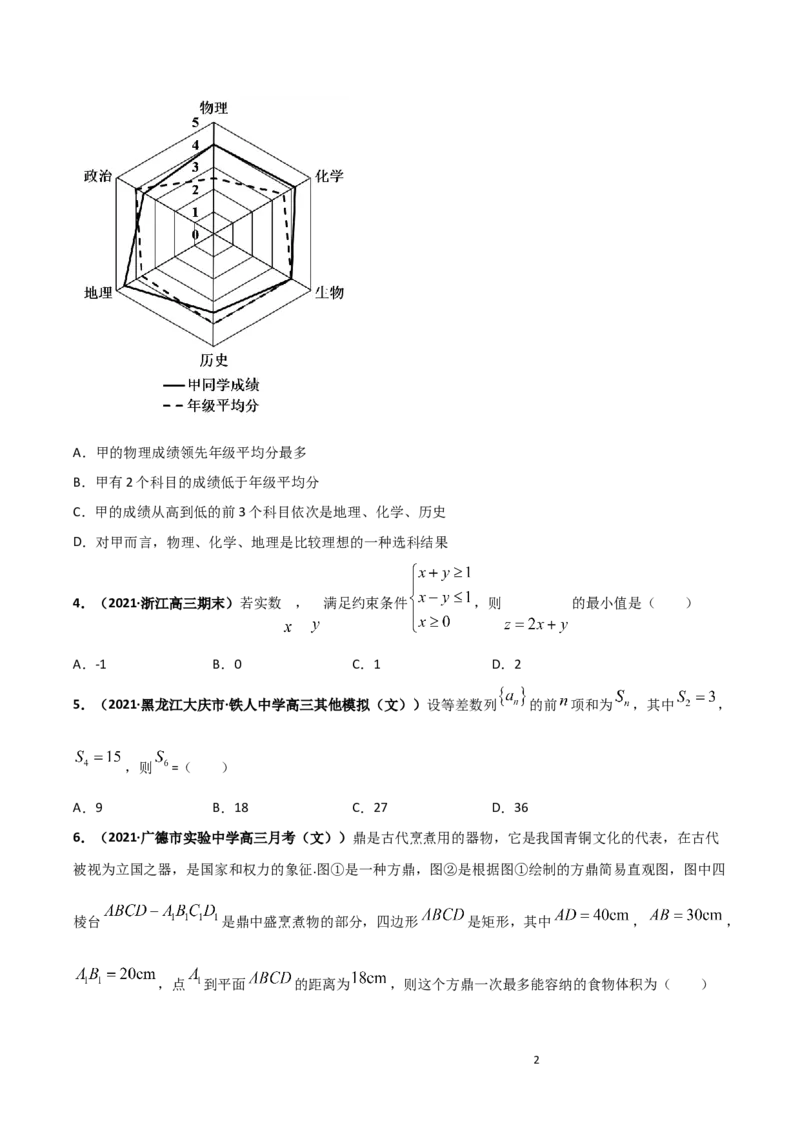
均缩放成5分制,绘制成雷达图.甲同学的成绩雷达图如图所示,下面叙述一定不正确的是( )
1A.甲的物理成绩领先年级平均分最多
B.甲有2个科目的成绩低于年级平均分
C.甲的成绩从高到低的前3个科目依次是地理、化学、历史
D.对甲而言,物理、化学、地理是比较理想的一种选科结果
4.(2021·浙江高三期末)若实数 , 满足约束条件 ,则 的最小值是( )
A.-1 B.0 C.1 D.2
5.(2021·黑龙江大庆市·铁人中学高三其他模拟(文))设等差数列 的前 项和为 ,其中 ,
,则 =( )
A.9 B.18 C.27 D.36
6.(2021·广德市实验中学高三月考(文))鼎是古代烹煮用的器物,它是我国青铜文化的代表,在古代
被视为立国之器,是国家和权力的象征.图①是一种方鼎,图②是根据图①绘制的方鼎简易直观图,图中四
棱台 是鼎中盛烹煮物的部分,四边形 是矩形,其中 , ,
,点 到平面 的距离为 ,则这个方鼎一次最多能容纳的食物体积为( )
2(假定烹煮的食物全在四棱台 内)
A. B. C. D.
7.(2021·新疆阿勒泰地区·布尔津县高级中学高三三模(理))已知函数 是定义在 上的偶函
数,且 ,当 时, ,要使方程 有且仅有5个零点,
则实数 的取值范围是( )
A. B.
C. D.
8.(2021·山东烟台市·高三二模)已知双曲线 : 的左、右焦点分别为 , ,
点 在 的右支上, 与 交于点 ,若 ,且 ,则 的离心率为( )
A. B. C. D.
3二、多择题:本大题共4小题,每个小题5分,共20分.
9.(2021·湖南高二月考) 的展开式中x的奇数次幂项的系数之和为64,则下列结论中正确
的是( )
A. B.展开式中常数项为3
C.展开式中 的系数为30 D.展开式中x的偶数次幂项的系数之和为64
10.(2021·全国高三专题练习)(多选题)已知数列{a }的前n项和为S ,a =1,S =S +2a +1,数列
n n 1 n+1 n n
的前n项和为T,n∈N*,则下列选项正确的为( )
n
A.数列{a +1}是等差数列
n
B.数列{a +1}是等比数列
n
C.数列{a }的通项公式为a =2n-1
n n
D.T<1
n
11.(2021·浙江高一期末)将函数 图象上所有点的横坐标伸长到原来的2倍,再向
右平移 个单位长度,得到函数 的图象,则下列说法正确的是( )
A.
B.函数 的图象关于点 对称
C. 是函数 的一条对称轴
D.函数 在 上单调递增
412.(2021·全国)已知函数 ,下列选项正确的是( )
A.函数 在 上单调递增
B.函数 的值域为
C.若关于 的方程 有3个不相等的实数根,则实数 的取值范围是
D.不等式 在 恰有两个整数解,则实数 的取值范围是
三、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13.(2018·全国高一课时练习)登山族为了了解某山高y(km)与气温x(℃)之间的关系,随机统计了4次山高
与相应的气温,并制作了对照表:
气温x(℃) 18 13 10 -1
山高y(km) 24 34 38 64
由表中数据,得到线性回归方程 =-2x+ ∈R),由此估计出山高为72(km)处的气温为_____℃.
14.(2021·凯里市第三中学高二月考)已知 点是椭圆 上的动点, 点是圆
上的动点,则线段 长度的最大值为_________.
15.(2020·全国高三专题练习(理))已知函数 ( ), ,若方
程 有三个实根 、 、 ,且 ,则 的值为
______.
516.(2020·全国高二课时练习)抛物线有如下光学性质:由其焦点射出的光线经抛物线反射后,沿平行于
抛物线对称轴的方向射出,今有抛物线 ,如图,一平行 轴的光线射向抛物线上的点 ,
经过抛物线的焦点 反射后射向抛物线上的点 ,再反射后又沿平行 轴方向射出,若两平行光线间的最
小距离为6,则此抛物线的方程为_______.
6四、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.
17.(2020·北京实验学校(海淀)高二期末)已知函数 .
(1)求函数 的单调区间;
(2)求函数 在 上的最大值和最小值.
18.(2021·山西高三三模(文))某知名品牌公司研发了一款自主品牌产品,按行业标准这款自主品牌产
品可分为一级正品、二级正品、次品共三个等级.根据该公司测算:生产出一件一级正品可获利 元,
一件二级正品可获利 元,一件次品亏损 元.该知名品牌公司试生产这款自主品牌产品 件,
并统计了这些产品的等级,如下表:
等级 一级正品 二级正品 次品
频数
(1)对于该知名品牌公司试生产出来的这 件产品,平均每件的产品利润是多少元?
(2)该知名品牌公司为了解消费者对这款自主品牌产品的满意度,随机调查了 名男性消费者和 名
女性消费者,每位消费者对这款自主品牌产品给出满意或不满意的评价,得到下面的列联表:
满意 不满意 总计
男性消费者
女性消费者
总计
问:能否在犯错误的概率不超过 的前提下认为男性消费者和女性消费者对这款自主品牌产品的评价
有差异?
附: ,其中 .
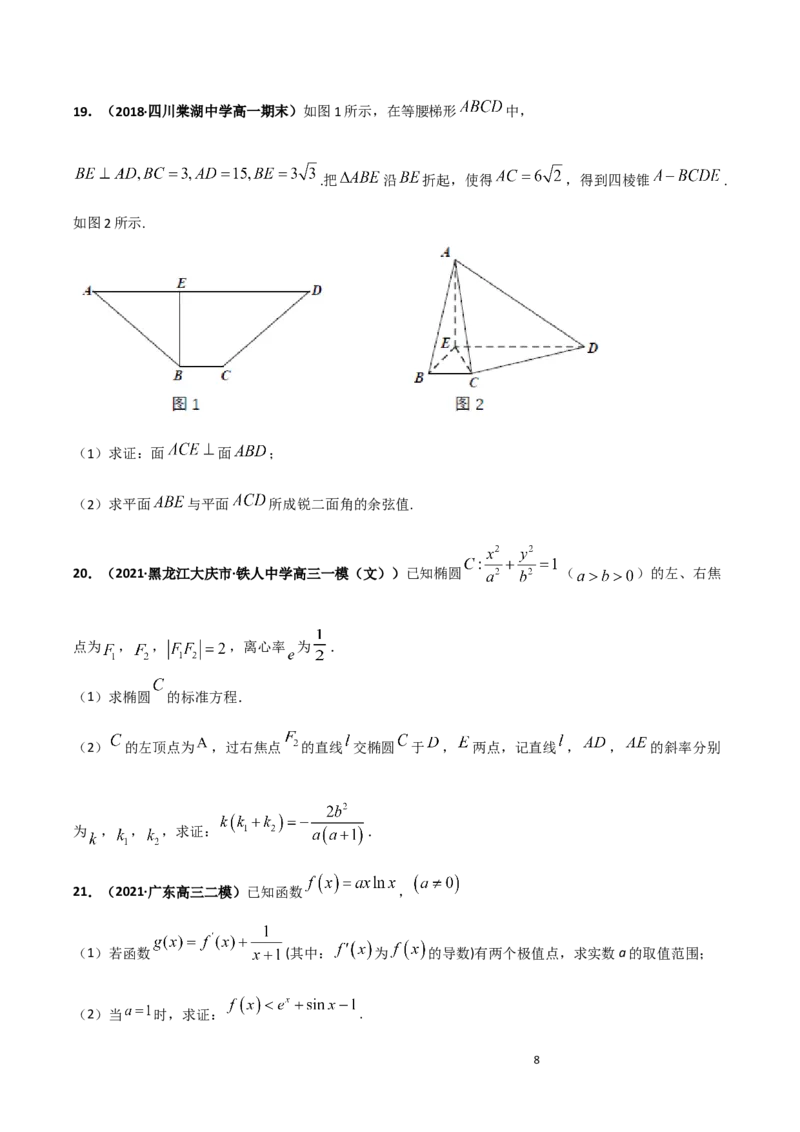
719.(2018·四川棠湖中学高一期末)如图1所示,在等腰梯形 中,
.把 沿 折起,使得 ,得到四棱锥 .
如图2所示.
(1)求证:面 面 ;
(2)求平面 与平面 所成锐二面角的余弦值.
20.(2021·黑龙江大庆市·铁人中学高三一模(文))已知椭圆 ( )的左、右焦
点为 , , ,离心率 为 .
(1)求椭圆 的标准方程.
(2) 的左顶点为 ,过右焦点 的直线 交椭圆 于 , 两点,记直线 , , 的斜率分别
为 , , ,求证: .
21.(2021·广东高三二模)已知函数 ,
(1)若函数 (其中: 为 的导数)有两个极值点,求实数a的取值范围;
(2)当 时,求证: .
822.(2021·贵州高三二模(理))在平面直角坐标系中,曲线 的参数方程为 (
为参数).以坐标原点 为极点, 轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
.
(Ⅰ)求曲线 的极坐标方程和曲线 的直角坐标方程;
(Ⅱ)已知直线 的极坐标方程为 , 分别与曲线 和 交于点 (异于点 )和点 ,
求线段 的长.
9