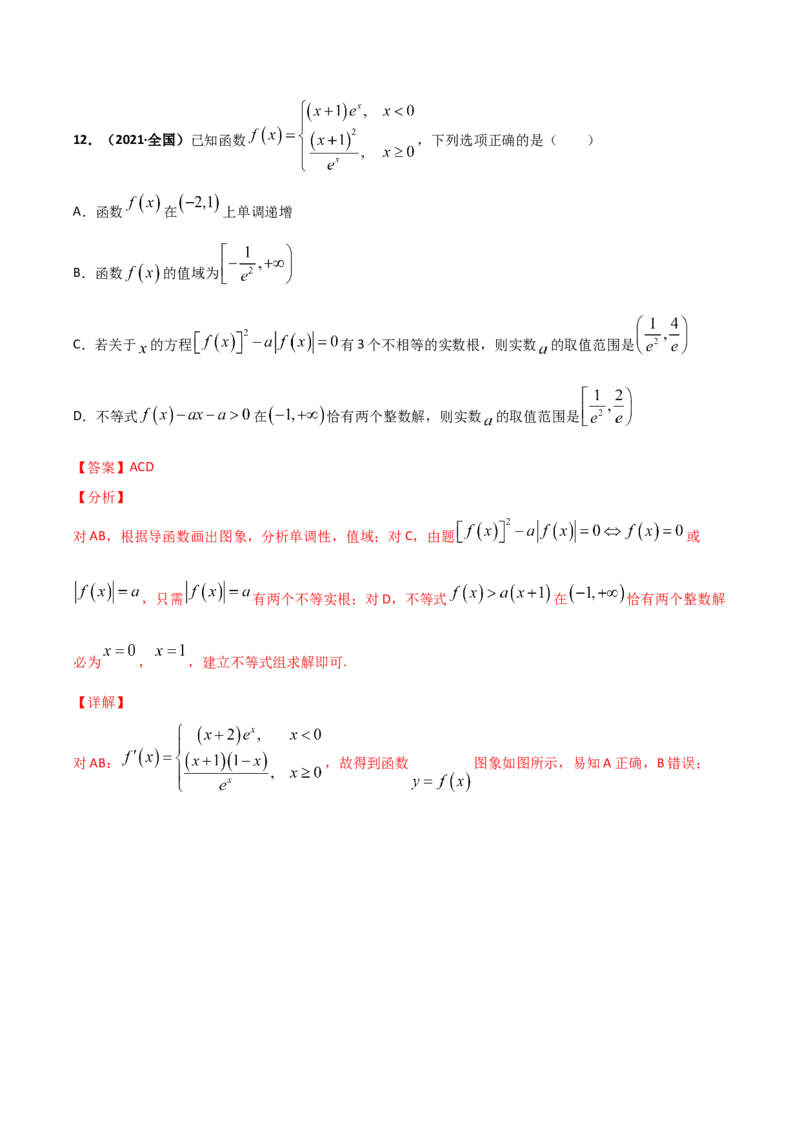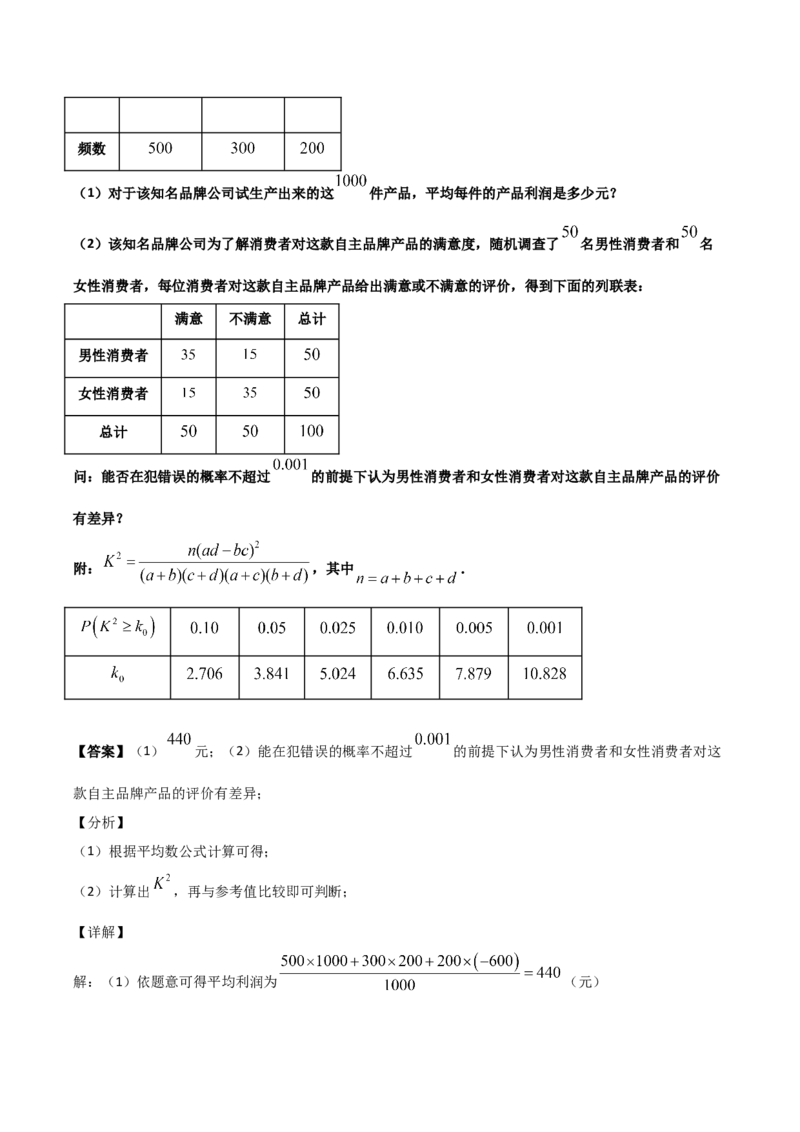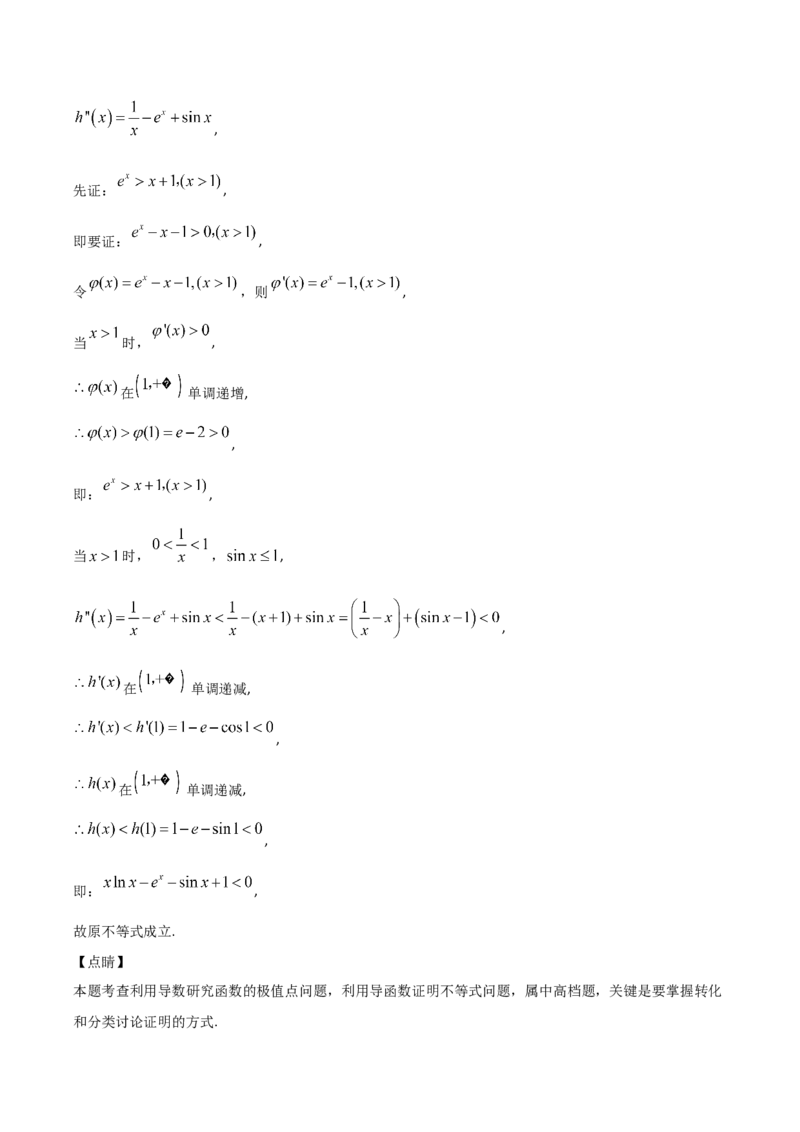文档内容
高二(下)期末测试卷(A 卷 基础巩固)
理科数学
考试时间:120分钟 满分:150分
一、选择题:本大题共8小题,每个小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要
求的.
1.(2021·黑龙江大庆市·铁人中学高三一模(文))复数 (其中 为虚数单位),则 的实部和
虚部的和为( )
A.2 B. C. D.
【答案】B
【分析】
根据复数的四则运算求得 ,从而获得复数 的实部和虚部,最后求解.
【详解】
由复数 ,
知 ,
则 .
故选B.
2.(2021·云南昆明一中高三其他模拟(文))设集合 , ,则 (
)
A. B. C. D.
【答案】A【分析】
求出集合 、 ,利用并集的定义可求得集合 .
【详解】
, ,因此, .
故选:A.
3.(2021·武威第六中学高三其他模拟(文))2021年开始,某省将试行“ ”的普通高考新模式,
即除物理语文、数学、外语3门必选科目外,考生再从物理、历史中选1门,从化学、生物、地理、政治
中选2门作为选考科目.为了帮助政治学生合理选科,某中学将高一每个学生的六门科目综合成绩按比例
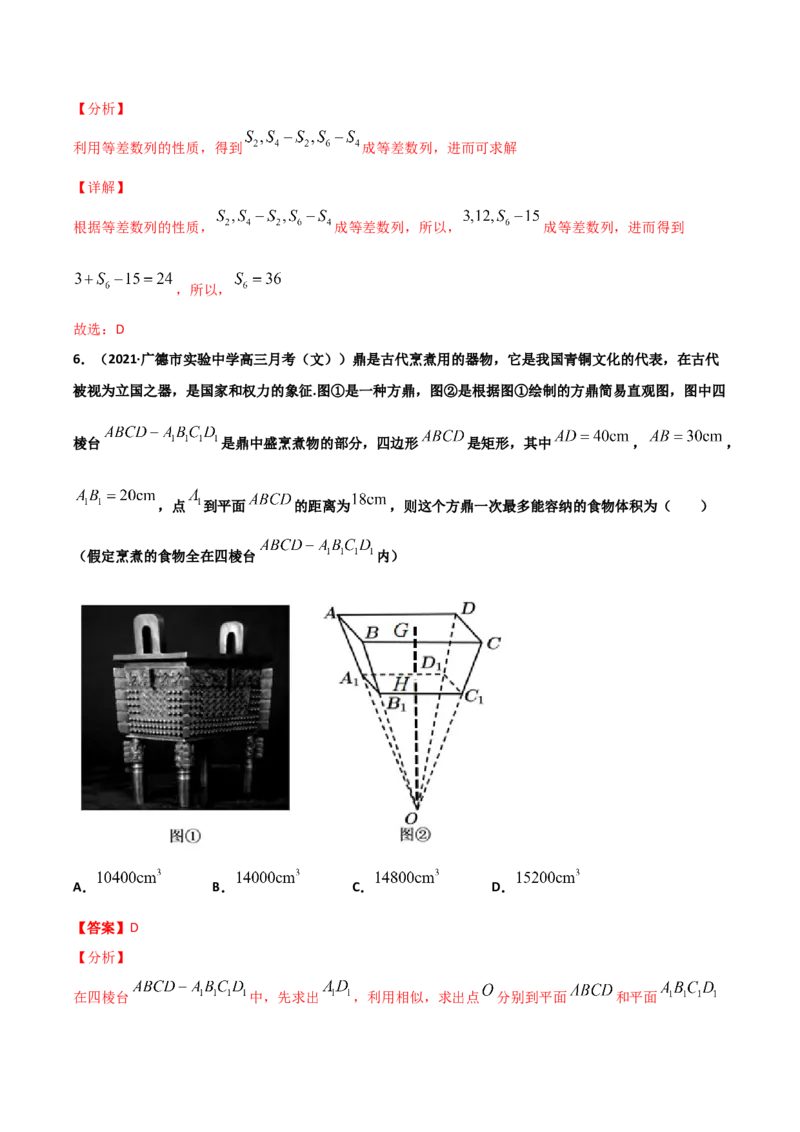
均缩放成5分制,绘制成雷达图.甲同学的成绩雷达图如图所示,下面叙述一定不正确的是( )
A.甲的物理成绩领先年级平均分最多
B.甲有2个科目的成绩低于年级平均分
C.甲的成绩从高到低的前3个科目依次是地理、化学、历史
D.对甲而言,物理、化学、地理是比较理想的一种选科结果
【答案】C
【分析】
根据雷达图,判断甲各科成绩与年级平均分的高低,以及各科成绩的高低,进而可确定理想的选科组合,
即可判断各选项的正误.
【详解】A:由图知:甲的物理成绩领先年级平均分1.5分左右,比化学、地理要高,正确;
B:其中有政治、历史比年级平均分低,正确;
C:甲的成绩从高到低的前3个科目依次是地理、化学、物理或生物,错误;
D:由C知:物理、化学、地理对于甲是比较理想的一种选科结果,正确;
故选:C.
4.(2021·浙江高三期末)若实数 , 满足约束条件 ,则 的最小值是( )
A.-1 B.0 C.1 D.2
【答案】C
【分析】
根据不等式组作出可行域,由目标函数的几何意义求得最小值.
【详解】
根据不等式组作出可行域,如图所示,
的最小值表示直线在y轴上的截距的最小值,即A点,易知 ,
此时 ,
故选:C
5.(2021·黑龙江大庆市·铁人中学高三其他模拟(文))设等差数列 的前 项和为 ,其中 ,
,则 =( )
A.9 B.18 C.27 D.36
【答案】D【分析】
利用等差数列的性质,得到 成等差数列,进而可求解
【详解】
根据等差数列的性质, 成等差数列,所以, 成等差数列,进而得到
,所以,
故选:D
6.(2021·广德市实验中学高三月考(文))鼎是古代烹煮用的器物,它是我国青铜文化的代表,在古代
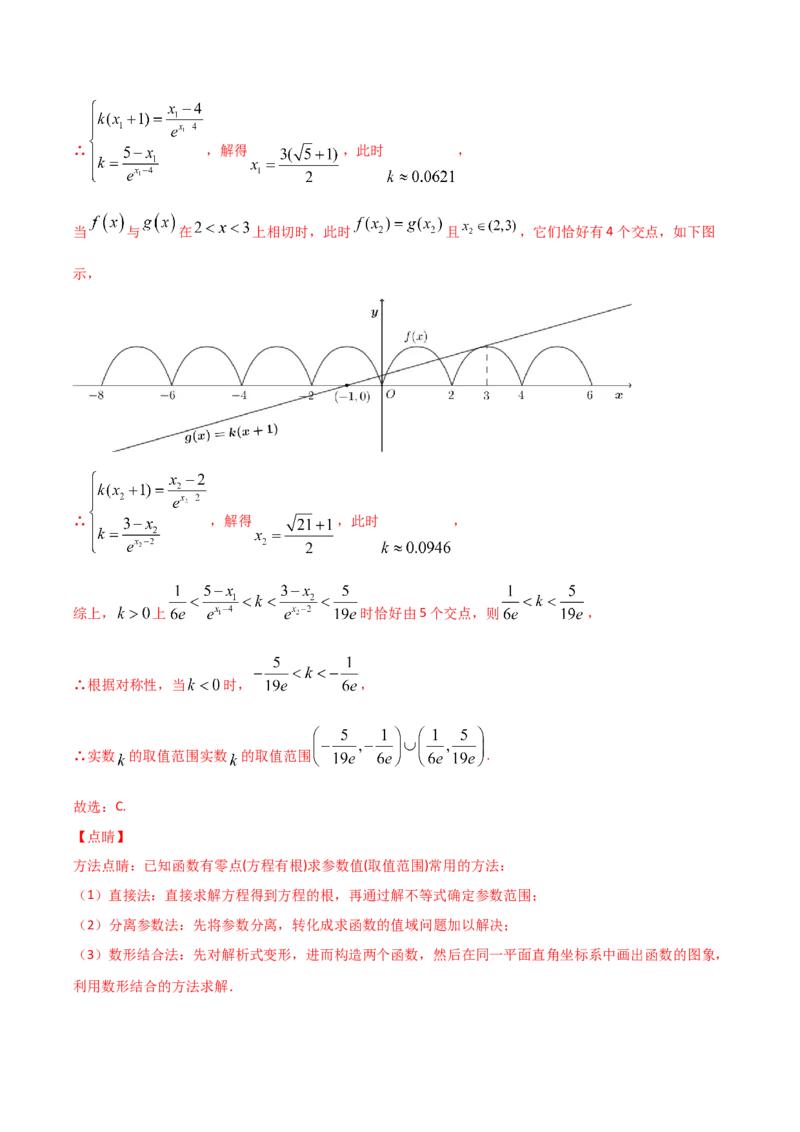
被视为立国之器,是国家和权力的象征.图①是一种方鼎,图②是根据图①绘制的方鼎简易直观图,图中四
棱台 是鼎中盛烹煮物的部分,四边形 是矩形,其中 , ,
,点 到平面 的距离为 ,则这个方鼎一次最多能容纳的食物体积为( )
(假定烹煮的食物全在四棱台 内)
A. B. C. D.
【答案】D
【分析】
在四棱台 中,先求出 ,利用相似,求出点 分别到平面 和平面的距离,进而求出四棱台 的体积.
【详解】
几何体 为四棱台,所以延长 必交于一点,记为O,
且四棱锥 相似于 ,所以 .过点 作OH⊥面
于H,
作OG⊥面 于G,则 ,又 ,解得:OG= ,OH= ,
四棱台 的体积
.
故选:D
【点睛】
求棱台的体积:
(1)直接利用体积公式求体积;
(2)利用分割法,大棱锥体积减去小棱锥的体积.
7.(2021·新疆阿勒泰地区·布尔津县高级中学高三三模(理))已知函数 是定义在 上的偶函
数,且 ,当 时, ,要使方程 有且仅有5个零点,
则实数 的取值范围是( )
A. B.C. D.
【答案】C
【分析】
由已知可得函数 的周期为2,令 ,则函数 恒过点 ,原问题转
化为函数 与 有且仅有5个交点,根据图象建立不等式组,解之可得所求范围.
【详解】
∵函数 是定义在 上的偶函数,
∴ ,又 ,则 ,
∴函数 的周期为2且 是一条对称轴,
当 时, ,则 ,
∴函数 单调递增,则 上 单调递减,
又 得: ,
令 恒过点 ,问题可化为 与 仅有5个交点,
当 时,当 与 在 上相切时,此时 且 ,它们恰好有6个交
点,如下图示,∴ ,解得 ,此时 ,
当 与 在 上相切时,此时 且 ,它们恰好有4个交点,如下图
示,
∴ ,解得 ,此时 ,
综上, 上 时恰好由5个交点,则 ,
∴根据对称性,当 时, ,
∴实数 的取值范围实数 的取值范围 .
故选:C.
【点睛】
方法点睛:已知函数有零点(方程有根)求参数值(取值范围)常用的方法:
(1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围;
(2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决;
(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,
利用数形结合的方法求解.8.(2021·山东烟台市·高三二模)已知双曲线 : 的左、右焦点分别为 , ,
点 在 的右支上, 与 交于点 ,若 ,且 ,则 的离心率为( )
A. B. C. D.
【答案】B
【分析】
由题设知△ 为等腰直角三角形,即 、 ,结合双曲线的定义
求 、 ,在△ 中应用余弦定理,构造齐次方程,求离心率即可.
【详解】
由 且 知:△ 为等腰直角三角形且 、 ,即
,
∵ ,
∴ ,故 ,则 ,
而在△ 中, ,
∴ ,则 ,故 .
故选:B.
【点睛】
关键点点睛:由已知条件判断△ 为等腰直角三角形,结合双曲线的定义及余弦定理可得齐次方程,
即可求离心率.二、多择题:本大题共4小题,每个小题5分,共20分.
9.(2021·湖南高二月考) 的展开式中x的奇数次幂项的系数之和为64,则下列结论中正确
的是( )
A. B.展开式中常数项为3
C.展开式中 的系数为30 D.展开式中x的偶数次幂项的系数之和为64
【答案】ABD
【分析】
设 ,分别令 和 ,两式相加减,即可判定A、D正
确;令 ,可判定B正确,结合二项展开式的系数求法,可判定C不正确.
【详解】
设 ,
令 ,则 ,……①
令 ,则 ,……②
由① ②得 ,所以 ,解得 ,
即 ,
令 ,可得 ,即展开式中常数项为3,
由① ②得 ,所以 ,
即展开式中x的偶数次幂项的系数之和为64,
又由 展开式中 的系数为 .
故选:ABD.
10.(2021·全国高三专题练习)(多选题)已知数列{a }的前n项和为S ,a =1,S =S +2a +1,数列
n n 1 n+1 n n的前n项和为T,n∈N*,则下列选项正确的为( )
n
A.数列{a +1}是等差数列
n
B.数列{a +1}是等比数列
n
C.数列{a }的通项公式为a =2n-1
n n
D.T<1
n
【答案】BCD
【分析】
由S =S +2a +1,得a +1=2(a +1),从而可得数列{a +1}是首项为2,公比为2的等比数列,进而
n+1 n n n+1 n n
得a =2n-1,则 = ,再利用裂项相消求和法求出T,从而可判断各项
n n
【详解】
由S =S +2a +1,得a =S -S =2a +1,可化为a +1=2(a +1).由a =1,得a +1=2,则数
n+1 n n n+1 n+1 n n n+1 n 1 1
列{a +1}是首项为2,公比为2的等比数列.则a +1=2n,即a =2n-1.
n n n
由 = = - ,
得T=1- + - +…+ - =1- <1.
n
所以A错误,B,C,D正确.
故选:BCD.
11.(2021·浙江高一期末)将函数 图象上所有点的横坐标伸长到原来的2倍,再向
右平移 个单位长度,得到函数 的图象,则下列说法正确的是( )
A.
B.函数 的图象关于点 对称C. 是函数 的一条对称轴
D.函数 在 上单调递增
【答案】BCD
【分析】
根据图象的伸缩变换以及平移变换先求解出 的解析式,然后再逐项分析 的对称中心、对称轴、
单调性.
【详解】
A.根据条件可知: ,故错误;
B.因为 ,所以 是 的一个对称中心,故正确;
C.因为 ,所以 是 的一条对称轴,故正确;
D.当 , ,因为 在 时单调递增,所以 在
上单调递增,
故选:BCD.
【点睛】
方法点睛:判断点 或直线 是否为函数 的对称中心或对称轴的常用方法:
(1)判断对称中心时,若 ,则 是 的一个对称中心,反之则不是;
(2)判断对称轴时,若 ,则 是 的一条对称轴,反之则不是.12.(2021·全国)已知函数 ,下列选项正确的是( )
A.函数 在 上单调递增
B.函数 的值域为
C.若关于 的方程 有3个不相等的实数根,则实数 的取值范围是
D.不等式 在 恰有两个整数解,则实数 的取值范围是
【答案】ACD
【分析】
对AB,根据导函数画出图象,分析单调性,值域;对C,由题 或
,只需 有两个不等实根;对D,不等式 在 恰有两个整数解
必为 , ,建立不等式组求解即可.
【详解】
对AB: ,故得到函数 图象如图所示,易知A正确,B错误;对D:不等式 在 恰有两个整数解,如图,必为 , ,故
,解得 ,故D对;
对C:如图为函数 的图象,则 或 ,因为方程有3个不相等的实数根,所以只需 有两个不等实根,故 ,
故C正确.
故选:ACD.
【点睛】
本题考查用导数研究函数的思路,以及方程有实根、整数解问题等,关键点在于能够将问题简化,从本质
入手进行分析.
三、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13.(2018·全国高一课时练习)登山族为了了解某山高y(km)与气温x(℃)之间的关系,随机统计了4次山高
与相应的气温,并制作了对照表:
气温x(℃) 18 13 10 -1
山高y(km) 24 34 38 64
由表中数据,得到线性回归方程 =-2x+ ∈R),由此估计出山高为72(km)处的气温为_____℃.
【答案】-6
【解析】
由题意可得 =10, =40,所以 +2 =40+2×10=60,所以 =-2x+60,当 =72时,-2x+60=72,解得x=-6.
14.(2021·凯里市第三中学高二月考)已知 点是椭圆 上的动点, 点是圆
上的动点,则线段 长度的最大值为_________.
【答案】
【分析】
求得圆的圆心和半径,由圆的对称性考虑圆心到椭圆上的点的距离的最大值,设椭圆上的点
, ,运用两点的距离公式和三角函数的基本关系式,正弦函数的性质即可求
得最大值.【详解】
由圆 可得圆心 ,半径为1,可考虑圆心到椭圆上的点的距离的最大值,
设椭圆上的点 , ,
则
当 时, 取得最大值 ,则 的最大值为
故答案为:
【点睛】
方法点睛:本题考查了椭圆的参数方程的运用,考查圆的对称性和两点之间距离公式的应用,解决椭圆中
的最值问题,一般有两种方法:一是几何法,特别是用椭圆的定义和平面几何的有关结论来解非常巧妙;
二是代数法,将椭圆中的最值问题转换为函数问题(即根据条件列出所求的目标函数),然后根据函数的特
征选用参数法、配方法、判别式法、三角有界法、函数单调性法即基本不等式法等,求解最大值或最小值.
15.(2020·全国高三专题练习(理))已知函数 ( ), ,若方
程 有三个实根 、 、 ,且 ,则 的值为
______.
【答案】16
【分析】
利用导数画出函数 的大致图象,数形结合可得 有两个不等实根,满足 、
,且 , ,即可得解.
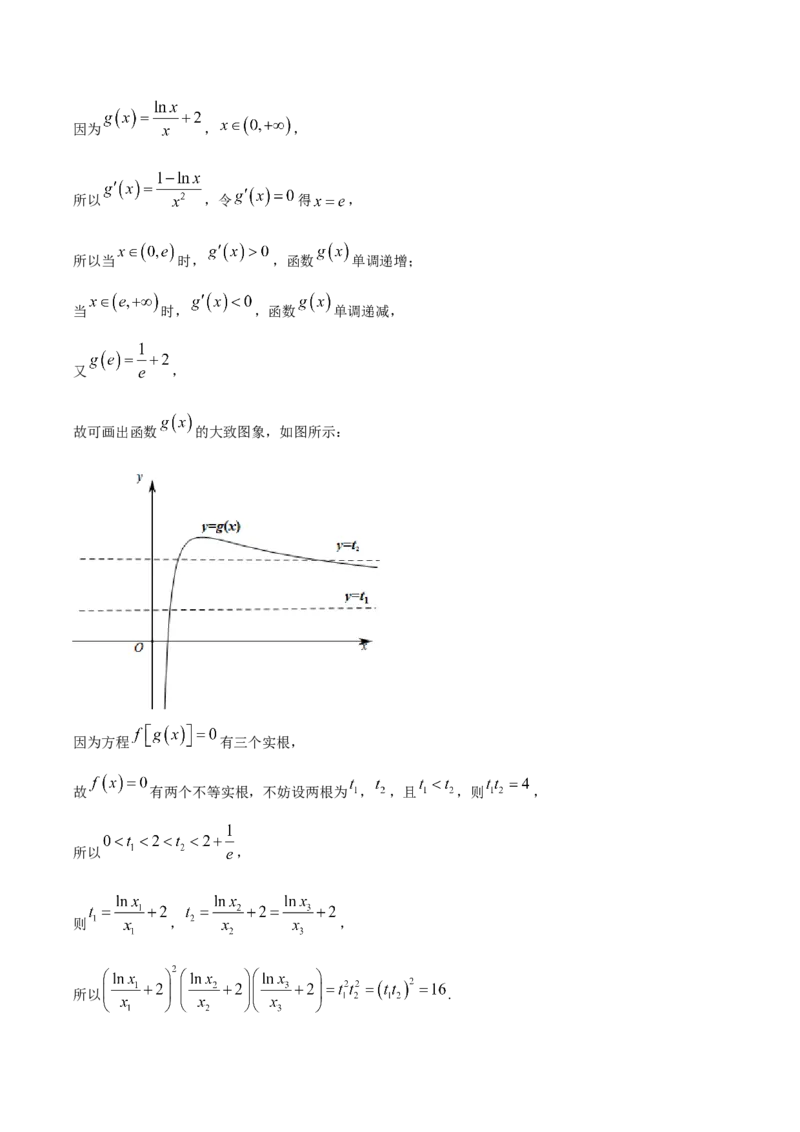
【详解】因为 , ,
所以 ,令 得 ,
所以当 时, ,函数 单调递增;
当 时, ,函数 单调递减,
又 ,
故可画出函数 的大致图象,如图所示:
因为方程 有三个实根,
故 有两个不等实根,不妨设两根为 , ,且 ,则 ,
所以 ,
则 , ,
所以 .故答案为:16.
【点睛】
本题考查了函数的零点与方程的根的关系,考查了利用导数研究函数的单调性和极值,属于中档题.
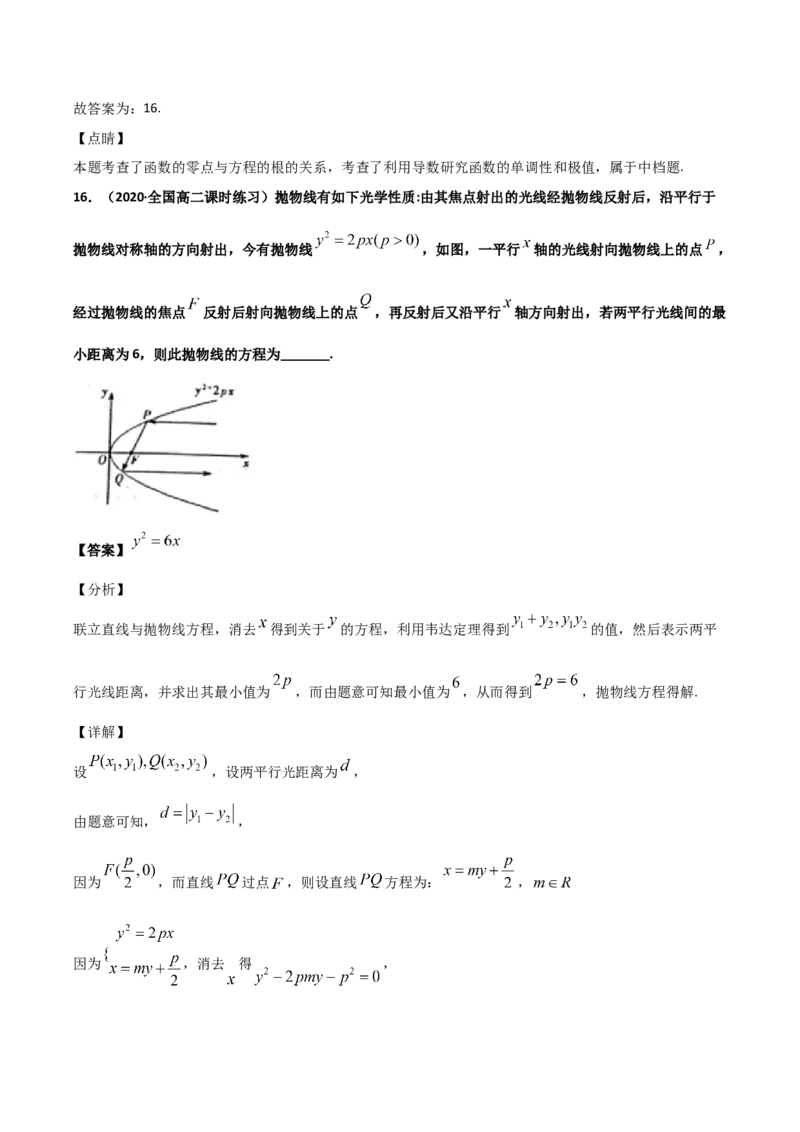
16.(2020·全国高二课时练习)抛物线有如下光学性质:由其焦点射出的光线经抛物线反射后,沿平行于
抛物线对称轴的方向射出,今有抛物线 ,如图,一平行 轴的光线射向抛物线上的点 ,
经过抛物线的焦点 反射后射向抛物线上的点 ,再反射后又沿平行 轴方向射出,若两平行光线间的最
小距离为6,则此抛物线的方程为_______.
【答案】
【分析】
联立直线与抛物线方程,消去 得到关于 的方程,利用韦达定理得到 的值,然后表示两平
行光线距离,并求出其最小值为 ,而由题意可知最小值为 ,从而得到 ,抛物线方程得解.
【详解】
设 ,设两平行光距离为 ,
由题意可知, ,
因为 ,而直线 过点 ,则设直线 方程为: ,
因为 ,消去 得 ,由韦达定理可得 ,
则 ,
所以 ,
故抛物线方程为 .
【点睛】
本题主要考查了抛物线方程的求解,涉及到韦达定理的应用,属于难题.对于涉及到直线与曲线相关的距离
问题,常常运用到韦达定理以及弦长公式进行求解.四、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.
17.(2020·北京实验学校(海淀)高二期末)已知函数 .
(1)求函数 的单调区间;
(2)求函数 在 上的最大值和最小值.
【答案】(1)区间 上单调递增;在区间 和 上单调递减;(2)5和1
【分析】
(1)区间 上单调递增;在区间 和 上单调递减
(2)5和1
【详解】
(1)因为函数 ,则
令 , 或
故函数 在区间 上单调递增;在区间 和 上单调递减
(2)由(1)可知函数 在区间 上单调递增;在 上单调递减
所以函数的极大值也为最大值
两端点 , ,即最小值为
故函数 在 上的最大值和最小值分别为5和1
【点睛】
本题考查利用导数研究函数单调性以及求最值,属于基础题.
18.(2021·山西高三三模(文))某知名品牌公司研发了一款自主品牌产品,按行业标准这款自主品牌产
品可分为一级正品、二级正品、次品共三个等级.根据该公司测算:生产出一件一级正品可获利 元,
一件二级正品可获利 元,一件次品亏损 元.该知名品牌公司试生产这款自主品牌产品 件,
并统计了这些产品的等级,如下表:
等级 一级正品 二级正品 次品频数
(1)对于该知名品牌公司试生产出来的这 件产品,平均每件的产品利润是多少元?
(2)该知名品牌公司为了解消费者对这款自主品牌产品的满意度,随机调查了 名男性消费者和 名
女性消费者,每位消费者对这款自主品牌产品给出满意或不满意的评价,得到下面的列联表:
满意 不满意 总计
男性消费者
女性消费者
总计
问:能否在犯错误的概率不超过 的前提下认为男性消费者和女性消费者对这款自主品牌产品的评价
有差异?
附: ,其中 .
【答案】(1) 元;(2)能在犯错误的概率不超过 的前提下认为男性消费者和女性消费者对这
款自主品牌产品的评价有差异;
【分析】
(1)根据平均数公式计算可得;
(2)计算出 ,再与参考值比较即可判断;
【详解】
解:(1)依题意可得平均利润为 (元)(2)依题意可得 ,所以能在犯错误的概率不超过 的前
提下认为男性消费者和女性消费者对这款自主品牌产品的评价有差异;
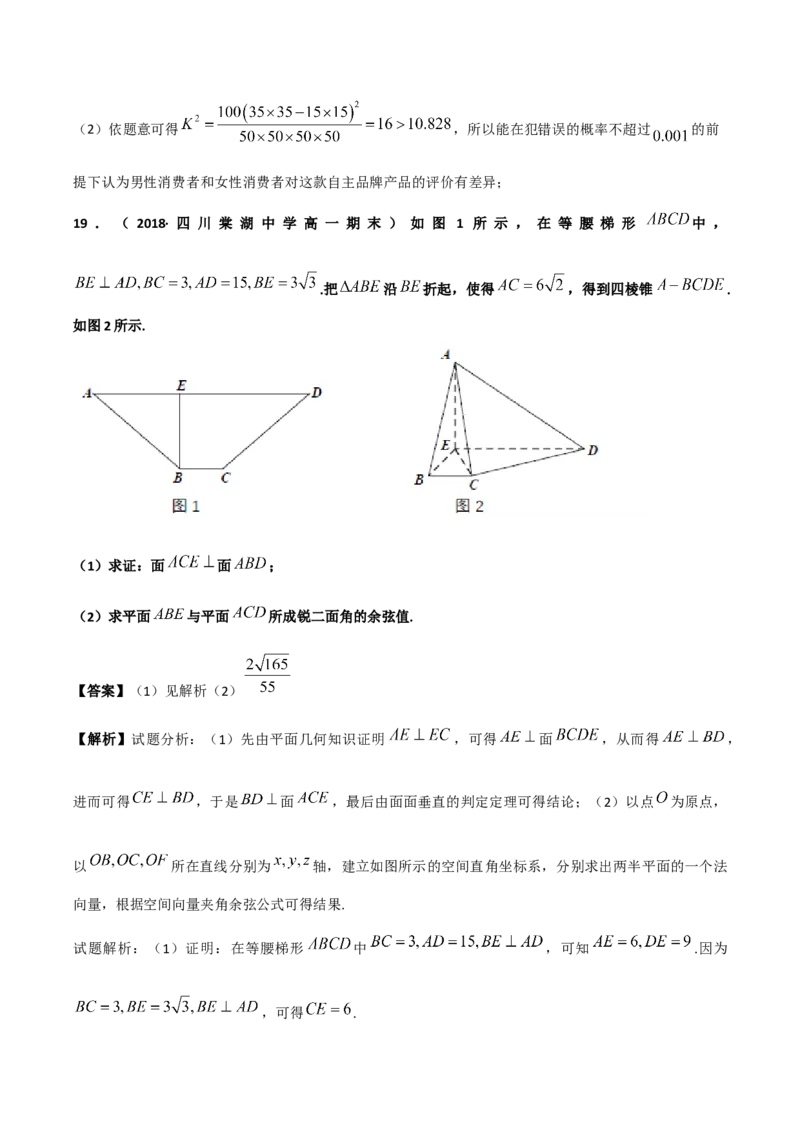
19 . ( 2018· 四 川 棠 湖 中 学 高 一 期 末 ) 如 图 1 所 示 , 在 等 腰 梯 形 中 ,
.把 沿 折起,使得 ,得到四棱锥 .
如图2所示.
(1)求证:面 面 ;
(2)求平面 与平面 所成锐二面角的余弦值.
【答案】(1)见解析(2)
【解析】试题分析:(1)先由平面几何知识证明 ,可得 面 ,从而得 ,
进而可得 ,于是 面 ,最后由面面垂直的判定定理可得结论;(2)以点 为原点,
以 所在直线分别为 轴,建立如图所示的空间直角坐标系,分别求出两半平面的一个法
向量,根据空间向量夹角余弦公式可得结果.
试题解析:(1)证明:在等腰梯形 中 ,可知 .因为
,可得 .又因为 ,即 ,则 .
又 ,可得 面 ,故 .
又因为 ,则 ,
,则 ,
所以 ,
又 ,所以 面 ,
又 面 ,所以面 面 ;
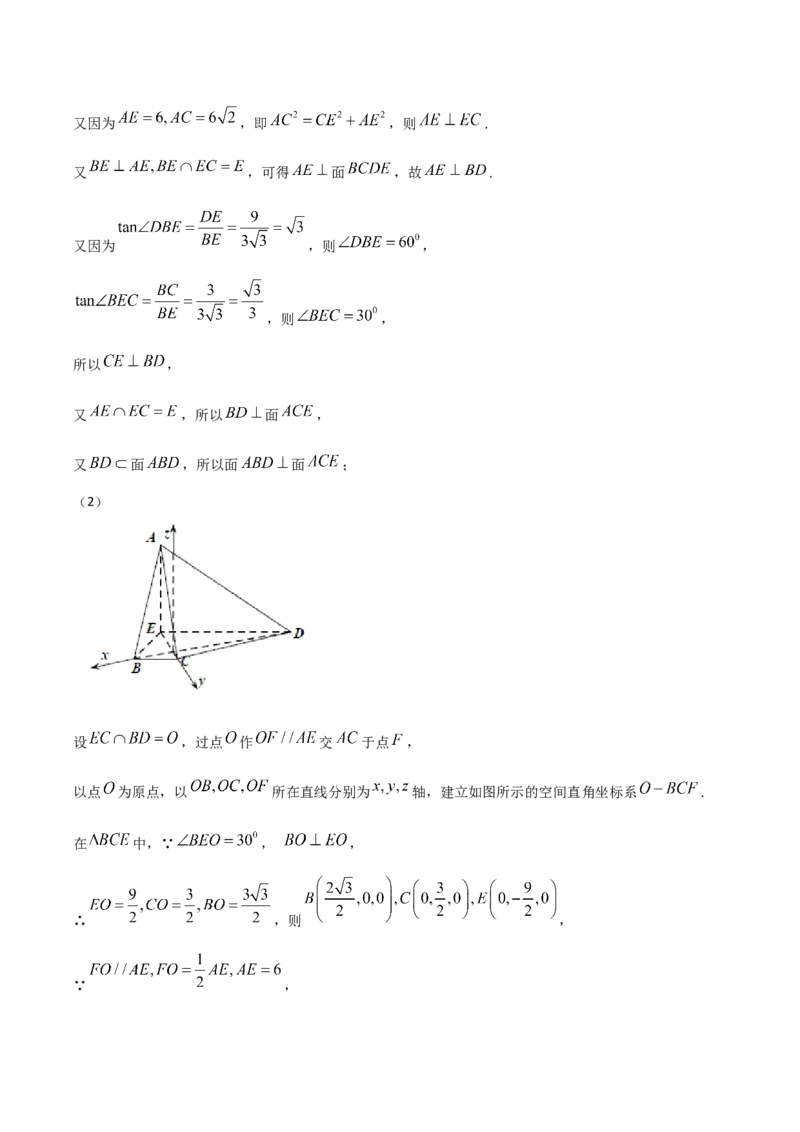
(2)
设 ,过点 作 交 于点 ,
以点 为原点,以 所在直线分别为 轴,建立如图所示的空间直角坐标系 .
在 中,∵ , ,
∴ ,则 ,
∵ ,∴ ,则 ,
∵ ,
∴ ,
∴ ,
∴ ,
设平面 的法向量为 ,
由 ,得 ,
取 ,可得平面 的法向量为 ,
设平面 的一个法向量为 ,
由 ,得 ,
取 ,可得平面 的一个法向量为 .
设平面 与平面 所成锐二面角为 ,
则 ,
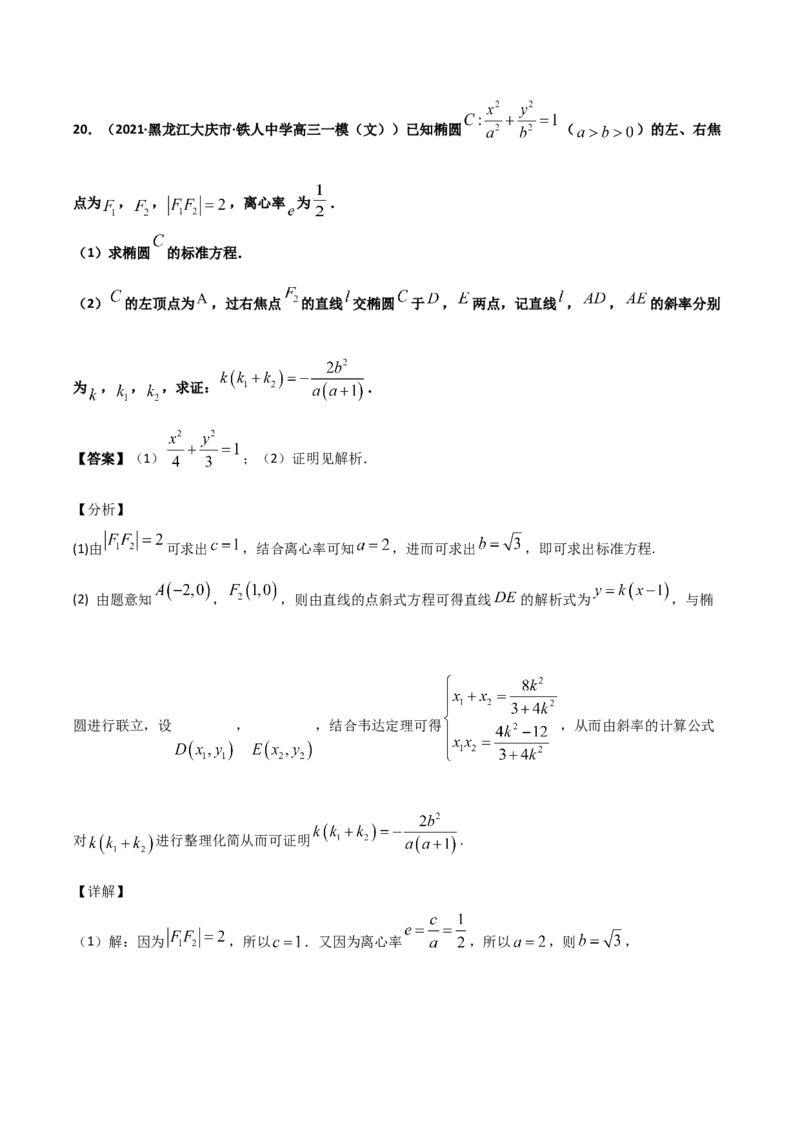
所以平面 与平面 所成锐二面角的余弦值为 .20.(2021·黑龙江大庆市·铁人中学高三一模(文))已知椭圆 ( )的左、右焦
点为 , , ,离心率 为 .
(1)求椭圆 的标准方程.
(2) 的左顶点为 ,过右焦点 的直线 交椭圆 于 , 两点,记直线 , , 的斜率分别
为 , , ,求证: .
【答案】(1) ;(2)证明见解析.
【分析】
(1)由 可求出 ,结合离心率可知 ,进而可求出 ,即可求出标准方程.
(2) 由题意知 , ,则由直线的点斜式方程可得直线 的解析式为 ,与椭
圆进行联立,设 , ,结合韦达定理可得 ,从而由斜率的计算公式
对 进行整理化简从而可证明 .
【详解】
(1)解:因为 ,所以 .又因为离心率 ,所以 ,则 ,所以椭圆 的标准方程是 .
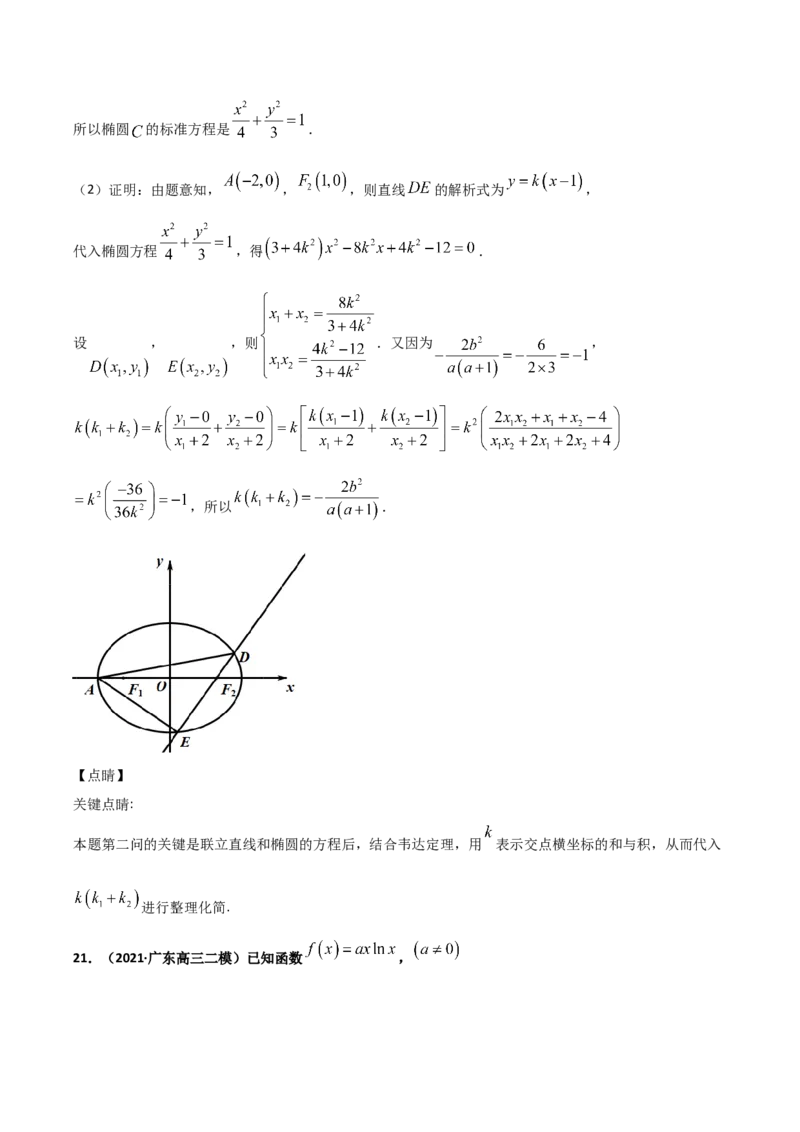
(2)证明:由题意知, , ,则直线 的解析式为 ,
代入椭圆方程 ,得 .
设 , ,则 .又因为 ,
,所以 .
【点睛】
关键点睛:
本题第二问的关键是联立直线和椭圆的方程后,结合韦达定理,用 表示交点横坐标的和与积,从而代入
进行整理化简.
21.(2021·广东高三二模)已知函数 ,(1)若函数 (其中: 为 的导数)有两个极值点,求实数a的取值范围;
(2)当 时,求证: .
【答案】(1) ;(2)证明见解析.
【分析】
(1)求得g(x)的导函数g'(x)后,根据g(x)有两个极值点的条件得到g'(x)在(0,+∞)上有两个变号零点,利用
二次方程的根的分布条件得到关于a的不等式组,求解即得所求;
(2)方法一:转化为证明 ,求得 ,先证明
,再证 进而得到 ,说明M(x)为单调递增函数,再分x∈[1,+∞)和x∈(0,1),结
合不等式的性质和三角函数的性质,即可证得所证不等式;
方法二:转化为证明 ,当01时转为证明 ,构造函数,利用导数研究函数的单调性,结合三角
函数的性质和不等式的基本性质即可证得.
【详解】
解:(1)依题意知: , ,
,
,
有两个极值点,
在 有两个变号零点,令 得: ①,
关于 的一元二次方程有两个不等的正根,记为 ,
即: ,
解得: , ,
故 的取值范围为: .
法1:
(二)当 ,
设
,
先证 ,
令 , ,当x>0时,g'(x)>0,
∴g(x)在[0,+∞)上单调递增,
又∵g(0)=0,
∴x>0时g(x)>0,即 .再证
令 ,
,
当00,h(x)单调递增;当x>1时h'(x)<0,h(x)单调递减.
∴h(x)≤h(1)=0,
∴ 成立,
,
时, 递增,
当 ,
当 , ,
,
, >0,命题得证;
法2
(2)依题意,要证: ,
①当 时, ,故原不等式成立,
②当 时,要证: ,
即要证: ,
令 ,
则 ,,
先证: ,
即要证: ,
令 ,则 ,
当 时, ,
在 单调递增,
,
即: ,
当 时, , ,
,
在 单调递减,
,
在 单调递减,
,
即: ,
故原不等式成立.
【点睛】
本题考查利用导数研究函数的极值点问题,利用导函数证明不等式问题,属中高档题,关键是要掌握转化
和分类讨论证明的方式.22.(2021·贵州高三二模(理))在平面直角坐标系中,曲线 的参数方程为 (
为参数).以坐标原点 为极点, 轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
.
(Ⅰ)求曲线 的极坐标方程和曲线 的直角坐标方程;
(Ⅱ)已知直线 的极坐标方程为 , 分别与曲线 和 交于点 (异于点 )和点 ,
求线段 的长.
【答案】(Ⅰ)曲线 的极坐标方程为 ,曲线 的直角坐标方程为:
;(Ⅱ)
【分析】
(Ⅰ)利用 消参后得到曲线 的普通方程,进而利用
可得曲线 的极坐标方程和曲线 的直角坐标方程;
(Ⅱ) 分别代入曲线 和曲线 的极坐标方程,求得 ,再利用公式 求
解.
【详解】
解:(Ⅰ)曲线 的直角坐标方程为 ,即 ,
因为 ,所以曲线 的极坐标方程为 ,
由 得 ,
又因为 ,
所以曲线 的直角坐标方程为: .
(Ⅱ)设
将 代入 得 ,
将 代入 得 ,
所以 .
【点睛】
方法点睛:本题考查弦长公式,一般求弦长的方法包含以下几点:
1.直角坐标系下的弦长公式 或是 ;
2.利用直线参数方程 的几何意义可知 ;
3.极坐标系下,过原点的直线与曲线相交的弦长 .