数学答案_2024年4月_01按日期_19号_2024届湖北省第九届高三下学期4月调研模拟考试_湖北省第九届2024届高三下学期4月调研模拟考试数学试卷

湖北省第九届高三（4 月）数学答案 1 2 3 4 5 6 7 8 9 10 11 D B D A D C A D BD BD ABC 1 12. 1 13. (2.25，4) 14.− 3 15．解：(1) 在三棱柱𝐴𝐵𝐶−𝐴 𝐵 𝐶 中，四边形𝐴 𝐴𝐶𝐶 是平行四边形，而𝐴𝐶 =𝐴𝐴 ，则平行四 1 1 1 1 1 1 边形𝐴 𝐴𝐶𝐶 是菱形，连接𝐴 𝐶，如图， 1 1 1 则有𝐴 𝐶 ⊥𝐴𝐶 ，因𝐴 𝐵 ⊥𝐴𝐶 ，𝐴 𝐵∩𝐴 𝐶 =𝐴 ， 1 1 1 1 1 1 1 𝐴 𝐵，𝐴 𝐶 ⊂平面𝐴 𝐵𝐶，于是得𝐴𝐶 ⊥平面𝐴 𝐵𝐶，…………………………………………………3分 1 1 1 1 1 而𝐵𝐶 ⊂平面𝐴 𝐵𝐶，则𝐴𝐶 ⊥𝐵𝐶，由∠𝐴𝐶𝐵 =90∘，得𝐴𝐶 ⊥𝐵𝐶，𝐴𝐶∩𝐴𝐶 =𝐴， 1 1 1 𝐴𝐶，𝐴𝐶 ⊂平面𝐴 𝐴𝐶𝐶 ， 1 1 1 从而得𝐵𝐶 ⊥平面𝐴 𝐴𝐶𝐶 ，……………………………………………………………………………6分 1 1 又𝐵𝐶 ⊂平面𝐴𝐵𝐶，所以平面𝐴 𝐴𝐶𝐶 ⊥平面𝐴𝐵𝐶．…………………………………………………7分 1 1 (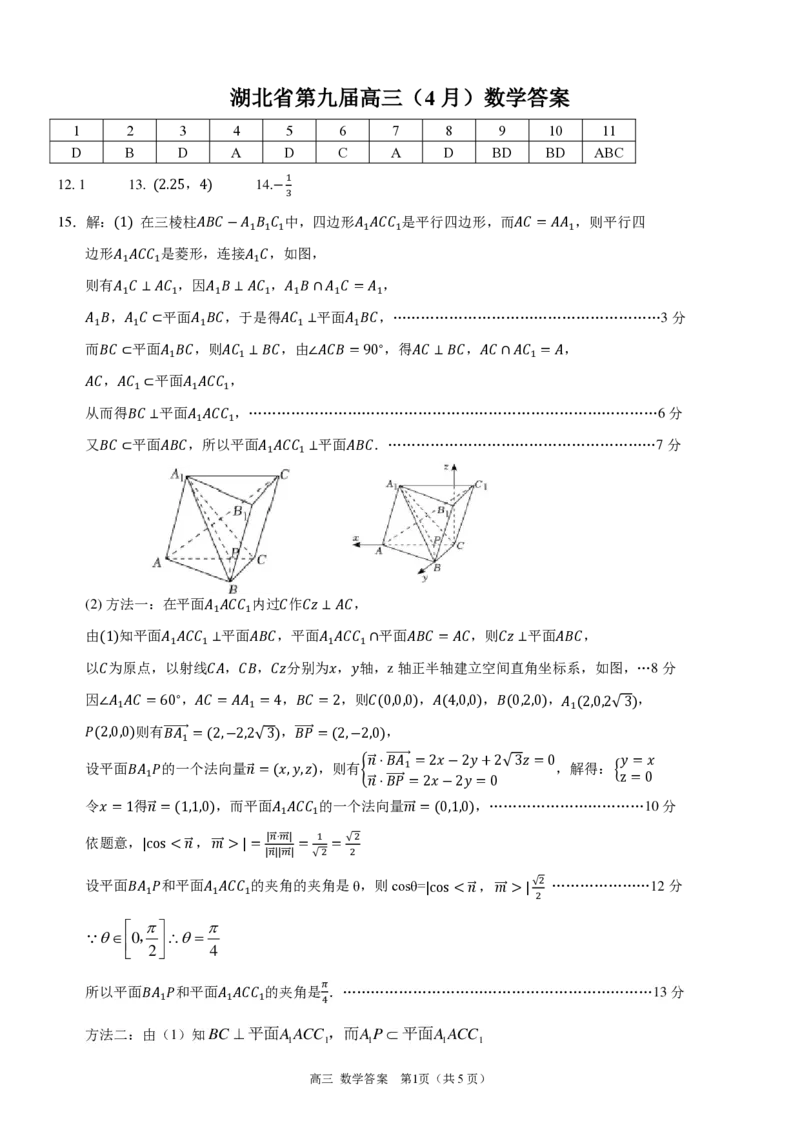2) 方法一：在平面𝐴 𝐴𝐶𝐶 内过𝐶作𝐶𝑧⊥𝐴𝐶， 1 1 由(1)知平面𝐴 𝐴𝐶𝐶 ⊥平面𝐴𝐵𝐶，平面𝐴 𝐴𝐶𝐶 ∩平面𝐴𝐵𝐶 =𝐴𝐶，则𝐶𝑧 ⊥平面𝐴𝐵𝐶， 1 1 1 1 以𝐶为原点，以射线𝐶𝐴，𝐶𝐵，𝐶𝑧分别为𝑥，𝑦轴，z轴正半轴建立空间直角坐标系，如图，…8分 因∠𝐴 𝐴𝐶 =60∘，𝐴𝐶 =𝐴𝐴 =4，𝐵𝐶 =2，则𝐶(0,0,0)，𝐴(4,0,0)，𝐵(0,2,0)，𝐴 (2,0,2√ 3)， 1 1 1 𝑃(2,0,0)则有𝐵⃗⃗⃗⃗⃗𝐴⃗⃗⃗ =(2,−2,2√ 3)，𝐵⃗⃗⃗⃗𝑃⃗ =(2,−2,0)， 1 𝑛⃗⃗ ⋅𝐵⃗⃗⃗⃗𝐴⃗⃗⃗ =2𝑥−2𝑦+2√ 3𝑧 =0 𝑦 =𝑥 设平面𝐵𝐴 𝑃的一个法向量𝑛⃗ =(𝑥,𝑦,𝑧)，则有{ 1 ，解得：{ 1 𝑛⃗⃗ ⋅𝐵⃗⃗⃗⃗𝑃⃗ =2𝑥−2𝑦=0 z=0 令𝑥 =1得𝑛⃗⃗ =(1,1,0)，而平面𝐴 𝐴𝐶𝐶 的一个法向量𝑚⃗⃗⃗ =(0,1,0)，……………………………10分 1 1 依题意，|cos<𝑛⃗⃗ ，𝑚⃗⃗⃗ >|= |𝑛⃗⃗ ·𝑚⃗⃗⃗ | = 1 = √ 2 |𝑛⃗⃗ ||𝑚⃗⃗⃗ | √ 2 2 设平面𝐵𝐴 𝑃和平面𝐴 𝐴𝐶𝐶 的夹角的夹角是θ，则cosθ=|cos<𝑛⃗⃗ ，𝑚⃗⃗⃗ >| √2 …………………12分 1 1 1 2     0， =    2 4 𝜋 所以平面𝐵𝐴 𝑃和平面𝐴 𝐴𝐶𝐶 的夹角是 ．…………………………………………………………13分 1 1 1 4 方法二：由（1）知BC ⊥平面AACC，而AP平面AACC 1 1 1 1 1 高三 数学答案 第1页（共5页） {#{QQABLQKAggioAJAAARgCQQUQCgOQkACCAKoOAFAEoAABiBFABAA=}#}AP ⊥ BC 1 在等边△AAC中，P为AC的中点，AP⊥ AC 1 1 又BCAC =C …………………………………………………………………………………9分 AP⊥平面ABC 1 又PC,PB在平面ABC内 CP ⊥ AP,BP ⊥ AP 1 1 ……………………………………………………11分 BPC即为二面角B−AP−C的平面角 1  在Rt△BCP,CB=CD=2,BPC= 4 𝜋 所以平面𝐵𝐴 𝑃和平面𝐴 𝐴𝐶𝐶 的夹角是 ．…………………………………………………………13分 1 1 1 4 16．解：(1) 样本中总共100人，其中旅游支出均不低于10000元的有33人，所以从中随机抽取两位市 𝐶2 33×32 8 民的旅游支出数据，两人旅游支出均不低于10000元的概率为𝑃 = 33 = = ；………4分 𝐶2 100×99 75 100 − 3 4 8 11 41 20 8 5 (2) (𝑖)计算𝑥 =1× +3× +5× +7× +9× +11× +13× +15× =9， 100 100 100 100 100 100 100 100 所以𝜇 =9，𝜎 =3，𝑋服从正态分布𝑁(9,32)，……………………………………………………6分 1 1 𝑃(𝑋 ≥15)=𝑃(𝑋 ≥9+2×3)= ×[1−𝑃(9−6≤𝑋 ≤9+6)]≈ ×(1−0.9545)=0.02275， 2 2 …………………………………………………………………………………………………………8分 500×0.02275=11.375(万)， 估计襄阳市有11.375万市民每年旅游费用支出在15000元以上；………………………………9分 1 (ⅱ)由(𝑖)知，𝜇 =9000，则𝑃(𝑋 >9000)= ，………………………………………………………10分 2 所有可能的取值为0，1，2，3. 𝑃(𝜉 =0)=𝐶0⋅(1− 1 )3 = 1 ， 𝑃(𝜉 =1)=𝐶1⋅ 1 ⋅(1− 1 )2 = 3 ， 3 2 8 3 2 2 8 𝑃(𝜉 =2)=𝐶2⋅( 1 )2⋅(1− 1 )= 3 ， 𝑃(𝜉 =3)=𝐶3⋅( 1 )3 = 1 ； 3 2 2 8 3 2 8 所以随机变量𝜉的分布列为： 𝜉 0 1 2 3 1 3 3 1 𝑃 8 8 8 8 …………………………………………………………14分 1 3 均值为𝐸(𝜉)=3× = ． ……………………………………………………………………………15分 2 2 高三 数学答案 第2页（共5页） {#{QQABLQKAggioAJAAARgCQQUQCgOQkACCAKoOAFAEoAABiBFABAA=}#}1 2𝑎𝑥[𝑥−( −1)] 17．解：(1)由题知，函数𝑓(𝑥)的定义域为(−1,+∞)，𝑓′(𝑥)= 2𝑎 ，………………………2分 1+𝑥 1 1 ①当0<𝑎 < 时，有 −1>0， 2 2𝑎 1 1 所以，𝑓(𝑥)在(−1,0)上单调递增，𝑓(𝑥)在(0, −1)上单调递减，𝑓(𝑥)在( −1,+∞)上单调递增； 2𝑎 2𝑎 …………………………………………………………………………………………………………4分 1 1 𝑥2 ②当𝑎 = 时，有 −1=0，𝑓′(𝑥)= ≥0， 2 2𝑎 1+𝑥 所以𝑓(𝑥)在(−1,+∞)上单调递增；…………………………………………………………………6分 1 1 ③当𝑎 > 时，有−1< −1<0， 2 2𝑎 1 1 所以，𝑓(𝑥)在(−1, −1)上单调递增，𝑓(𝑥)在( −1,0)上单调递减，𝑓(𝑥)在(0,+∞)上单调递增． 2𝑎 2𝑎 …………………………………………………………………………………………………………8分 1 (2)由(1)知：当𝑎 = 时，𝑓(𝑥)在(0,1)上单调递增， 2 𝑥2 所以，当𝑥 ∈(0,1)时，𝑓(𝑥)>𝑓(0)=0，即 >𝑥−ln(1+𝑥)=𝑔(𝑥)，………………………13分 2 𝜋 𝛼 ∈(0, )，sin𝛼 ∈(0,1),cos𝛼 ∈(0,1), 2 sin2𝛼+cos2𝛼 1 所以𝑔(sin𝛼)+𝑔(cos𝛼)< = .……………………………………………………………15分 2 2 18．解：(1) 设𝑀(𝑥,𝑦)，又𝐴 ( 2𝑖 ,0)，𝐵 (2,√ 3− √ 3𝑖 )(𝑖 =1,2,3⋯,𝑛−1)， 𝑖 𝑖 𝑖 𝑛 𝑛 则直线𝐸𝐴 :𝑦+√ 3= √ 3𝑛 𝑥，① 𝑖 2𝑖 直线𝐺𝐵:𝑦−√ 3=− √ 3𝑖 𝑥， ②………………………………………………………………………3分 𝑖 2𝑛 点𝑀(𝑥,𝑦)的坐标是方程①②的解，①×②可得(𝑦+√ 3)(𝑦−√ 3)=− 3 𝑥2， 𝑖 4 𝑥2 𝑦2 化简得 + =1， 4 3 𝑥2 𝑦2 所以𝑀(𝑥,𝑦)在同一个椭圆上，该椭圆方程为 + =1．………………………………………6分 𝑖 4 3 (2) 设𝐴(𝑥 ,𝑦 )，𝐵(𝑥 ,𝑦 )，𝑃(𝑥 ,𝑦 )，则𝑥2+𝑦2 =7， 1 1 2 2 0 0 0 0 切线𝑃𝐴方程为： 𝑥1𝑥 + 𝑦1𝑦 =1，切线𝑃𝐵方程为： 𝑥2𝑥 + 𝑦2𝑦 =1，两直线都经过点P， 4 3 4 3 所以得： 𝑥1𝑥0+ 𝑦1𝑦0 =1， 𝑥2𝑥0+ 𝑦2𝑦0 =1，从而直线𝐴𝐵的方程是： 𝑥0𝑥+ 𝑦0𝑦 =1，……………8分 4 3 4 3 4 3 当𝑦 =0时，𝑥2 =7 0 0 𝑥0𝑥 =1 由{ 4 得𝑦2 = 9 ，则|𝐴𝐵|=|y −y |= 6 𝑥2 + 𝑦2 =1 7 1 2 √7 4 3 1 6 4 9 S =  ( 7− )= …………………………………………………………………………9分 2 7 7 7 当𝑦 ≠0时， 0 高三 数学答案 第3页（共5页） {#{QQABLQKAggioAJAAARgCQQUQCgOQkACCAKoOAFAEoAABiBFABAA=}#}𝑥0𝑥+ 𝑦0𝑦 =1 由{ 4 3 ，消𝑦得：(𝑦2+21)𝑥2−24𝑥 𝑥+48−16𝑦2 =0， 𝑥2 𝑦2 0 0 0 + =1 4 3 由韦达定理，得：𝑥 +𝑥 = 24𝑥0 ，𝑥 𝑥 = 48−16𝑦 0 2 ，……………………………………………11分 1 2 𝑦 0 2+21 1 2 𝑦 0 2+21 |𝑥 −𝑥 |=√ ( 24𝑥0 )2−4⋅ 48−16𝑦 0 2 = 8|𝑦0 |√𝑦 0 2+9 ， 1 2 𝑦2+21 𝑦2+21 𝑦2+21 0 0 0 |𝐴𝐵|=√ 1+(− 3𝑥0)2⋅|𝑥 −𝑥 |=√ 1+ 9𝑥 0 2 ⋅ 8|𝑦0 |√𝑦 0 2+9 = 2√7(𝑦 0 2+9)， 4𝑦0 1 2 16𝑦 0 2 𝑦 0 2+21 𝑦 0 2+21 点P到直线𝐴𝐵的距离𝑑 = | 𝑥 4 0 2 + 𝑦 3 0 2 −1| = √ 𝑦 0 2+9 ， √ ( 𝑥0)2+( 𝑦0)2 √ 7 4 3 1 1 2 7(y2 +9) y2 +9 ( y2 +9)3 S = AB d =  0  0 = 0 其中0<𝑦2 ≤7…………………14分 2 2 y2 +21 7 y2 +21 0 0 0 令𝑡 =√ 𝑦2+9，则𝑡 ∈(3,4]，∴𝑆 = 𝑡3 ，令𝑓(𝑡)= 𝑡3 ，则𝑓′(𝑡)= 𝑡4+36𝑡2 >0， 0 △𝑃𝐴𝐵 𝑡2+12 𝑡2+12 (𝑡2+12)2 9 16 ( ) ∴𝑓(𝑡)在𝑡 ∈(3,4]上单调递增， f t  , .………………………………………………16分  7 7  9 16 综上所述，△𝑃𝐴𝐵面积的取值范围是 , .……………………………………………………17分   7 7  19．解：(1) 由题意，可知𝑎 =𝑎 +𝑚×(3−1)=2𝑚+2， 31 11 𝑎 =𝑎 ·𝑚 =(2𝑚+2)𝑚 =2𝑚(𝑚+1)，𝑎 =𝑎 +𝑚×(4−1)=3𝑚+2， 32 31 41 11 1 1 ∵𝑎 = 𝑎 +2，∴3𝑚+2= ×2𝑚(𝑚+1)+2， 41 32 2 2 化简整理，得𝑚2−2𝑚 =0， 解得𝑚 =0(舍去)，或𝑚 =2，………………………………………………………………………4分 ∴𝑎 =𝑎 +𝑚×(5−1)=2+2×4=10， 51 11 ∴𝑎 =𝑎 ·𝑚2 =10×22 =40，……………………………………………………………………5分 53 51 （2）a =a 2j−1 =  2+(i−1)2  2j−1 =i2j……………………………………………………6分 ij i1   ∴a =n2j =n(3−1)j =n3j +c13j−1(−1)+c23j−2(−1)2 ++cj−13(−1)j−1+(−1)j nj j j j   =n3m+(−1)j =3nm+n(−1)j ∴b 等于n(−1)j除以3的余数.…………………………………………………………………7分 nj 当j为奇数时n(−1)j =−n. ①n=3k−2(kN*)时，−n=−(3k−2)=−3k+2，b =2 (3k−2)j ②n=3k−1(kN*)时，−n=−(3k−1)=−3k+1，b =1 (3k−1)j 高三 数学答案 第4页（共5页） {#{QQABLQKAggioAJAAARgCQQUQCgOQkACCAKoOAFAEoAABiBFABAA=}#}③n=3k(kN*)时，−n=−3k，b =0………………………………………………………8分 (3k)j 当j为偶数时n(−1)j =n. ①n=3k−2(kN*)时，n=3k−2=3(k−1)+1，b =1 (3k−2)j ②n=3k−1(kN*)时，n=3k−1=3(k−1)+2，b =2 (3k−1)j ③n=3k(kN*)时，n=3k+0，b =0……………………………………………………9分 (3k)j c =b +b ++b =(2+1)+(2+1)++(2+1)+2=3(3m−3)+2=9m−7 6m−5 (6m−5)1 (6m−5)2 (6m−5)(6m−5)  3m−3个 c =b +b ++b =(1+2)+(1+2)++(1+2)+(1+2)=3(3m−2)=9m−6 6m−4 (6m−4)1 (6m−4)2 (6m−4)(6m−4)  3m−2个 c =b +b ++b =0+0++0=0 6m−3 (6m−3)1 (6m−3)2 (6m−3)(6m−3) c =b +b ++b =(2+1)+(2+1)++(2+1)=3(3m−1)=9m−3 6m−2 (6m−2)1 (6m−2)2 (6m−2)(6m−2)  3m−1个 c =b +b ++b =(1+2)+(1+2)++(1+2)+1=3(3m−1)+1=9m−2 6m−1 (6m−1)1 (6m−1)2 (6m−1)(6m−1)  3m−1个 c =b +b ++c =0+0++0=0………………………………………12分 6m (6m)1 (6m)2 (6m)(6m) mN*时，c +c +c +c +c +c =36m−18………………………13分 6m−5 6m−4 6m−3 6m−2 6m−1 6m (18+36k−18)k n 9n2 当n=2k(kN*)时，T =T = =18k2 =18( )2 = 3n 6k 2 2 2 当n=2k−1(kN*)时，T =T =T −c −c −c =18k2 −0−(9k−2)−(9k−3) 3n 6k−3 6k 6k 6k−1 6k−2 n+1 n+1 9n2 +1 =18k2 −18k+5=18( )2 −18 +5= 2 2 2 9n2 ，n为偶数.   2 综上，T = ………………………………………………………17分 3n 9n2 +1 ，n为奇数.   2 高三 数学答案 第5页（共5页） {#{QQABLQKAggioAJAAARgCQQUQCgOQkACCAKoOAFAEoAABiBFABAA=}#}