文档内容
乌鲁木齐地区 2024 年高三年级第一次质量监测
数学(问卷)
(卷面分值:150分;考试时间:120分钟)
注意事项:
1.本试卷分为问卷(4页)和答卷(4页),答案务必书写在答卷(或答题卡)的指定位量上.
2.答题前,先将答卷密封线内的项目(或答题卡中的相关信息)填写清楚.
第I卷(选择题 共58分)
一、选择题:本大题共8小题,每小题5分,共计40分.在每小题给出的四个选项中只有一项
是符合题目要求的.请把正确的选项填涂在答题卡相应的位置上.
1.若复数 ,则 ( )
A. B. C.1 D.
2.命题“ , ”的否定是( )
A. , B. ,
C. , D. ,
3.已知向量 , ,则( )
A. B.
C. D.
4.已知数列 满足 , ,则 ( )
A.3 B.2或 C.3或 D.2
5. 的展开式中 的系数为( )
A. B. C.20 D.30
6.设抛物线 的焦点为 ,过点 且倾斜角为 的直线与 交于A,B两点,以 为
直径的圆与准线 切于点 ,则 的方程为( )
学科网(北京)股份有限公司A. B. C. D.
7.在 中, , , ,则下列各式一定成立的是( )
A. B.
C. D.
8.在满足 , 的实数对 中,使得 成立的
正整数 的最大位为( )
A.15 B.16 C.22 D.23
二、选择题:本大题共3小题,每小题6分,共计18分.在每小题给出的四个选项中,有多项
符合题目要求.全部选对得6分,部分选对得部分分,有选错的得0分.
9.已知函数 的部分图像如图所示,则( )
A. 在 上单调递增
B. 在 上有4个零点
C.
D.将 的图祭向右平移 个单位,可得 的图急
10.若函数 的定义域为 ,且 , ,则( )
A. B. 为偶函数
C. 的图象关于点 对称 D.
11.某广场设置了一些石凳供大家休息,这些石凳是由棱长为40cm的正方体截去八个一样的四面体得到的,
学科网(北京)股份有限公司则( )
A.该几何体的顶点数为12
B.该几何体的棱数为24
C.该几何体的表面积为
D.该几何体外接球的表面积是原正方体内切球、外接球表面积的等差中项
第II卷(非选择题 共92分)
三、填空题:本大题共3小题,每小题5分,共计15分.
12.已知集合 , ,则 的子集个数为
_________;
13.在工业生产中轴承的直径服从 ,购买者要求直径为 ,不在这个范围的将被拒绝,
要使拒绝的概率控制在 之内,则 至少为_________;(若 ,则
)
14.设双曲线 的左、右焦点分别为 , ,A是右支上一点,满足 ,
直线 交双曲线于另一点 ,且 ,则双曲线离心率的一个值为_________.
四、解答题:本大题共5小题,共计77分.解答应在答卷的相应各题中写出文字说明,证明过
程或演算步骤.
15.(13分)设等比数列 的前 项和为 ,已知 , .
(I)求 的通项公式;
(II)设 ,求 的前 项和 .
16.(15分)我们平时常用的视力表叫做对数视力表,视力呈现为4.8,4.9,5.0,5.1.视力 为正常视
力.否则就是近视.某地区对学生视力与学习成结进行调查,随机抽查了100名近视学生的成绩,得到频率
分布直方图:
学科网(北京)股份有限公司(I)能否据此判断学生的学习成绩与视力状况相关?(不需说明理由)
(II)估计该地区近视学生学习成缆的第85百分位数;(精确到0.1)
(III)已知该地区学生的近视率为54%,学生成绩的优秀率为36%(成绩 分为优秀),从该地区学生中
任选一人,若此人的成绩为优秀,求此人近视的概率.(以样本中的频率作为相应的概率)
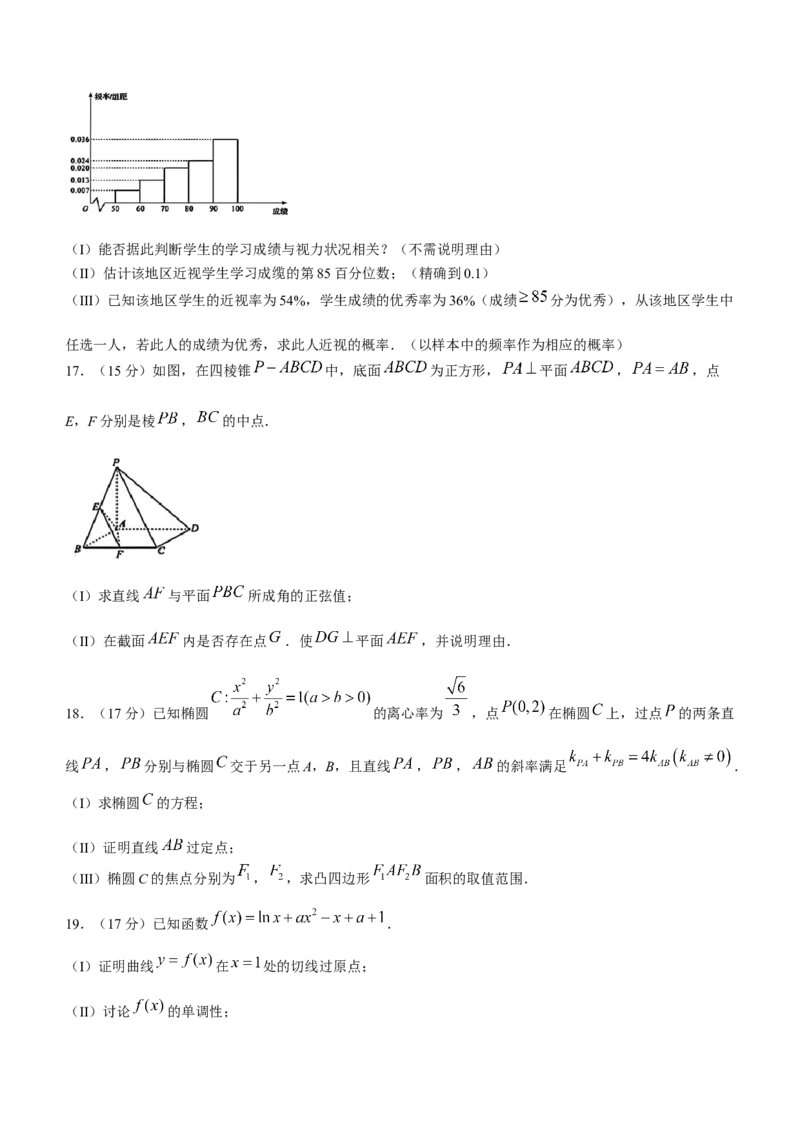
17.(15分)如图,在四棱锥 中,底面 为正方形, 平面 , ,点
E,F分别是棱 , 的中点.
(I)求直线 与平面 所成角的正弦值;
(II)在截面 内是否存在点 .使 平面 ,并说明理由.
18.(17分)已知椭圆 的离心率为 ,点 在椭圆 上,过点 的两条直
线 , 分别与椭圆 交于另一点A,B,且直线 , , 的斜率满足 .
(I)求椭圆 的方程;
(II)证明直线 过定点;
(III)椭圆C的焦点分别为 , ,求凸四边形 面积的取值范围.
19.(17分)已知函数 .
(I)证明曲线 在 处的切线过原点;
(II)讨论 的单调性;
学科网(北京)股份有限公司(III)若 ,求实数 的取值范围.
乌鲁木齐地区2024年高三年级第一次质量监测
数学(答案)
一、选择题:本大题共8小题,每小题5分,共计40分.
1~4ACDC 5~8ABBD
二、选择题:本大题共3小题,每小题6分,共计18分.在每小题给出的四个选项中,有多项
符合题目要求.全部选对得6分,部分选对得部分分,有选错的得0分.
9.ABC 10.BCD 11.ABD
三、填空题:本大题共3小题,每小题5分,共计15分.
12.4 13.0.1 14. 或5
四、解答题:本大题共5小题,共计77分.解答应在答卷的相应各题中写出文字说明,证明过
程或演算步骤.
15.(13分)(I)由题设得 ,故 ,
因为数列 为等比数列,所以数列 ,所以 ;
(II)由(I)得 ,
所以 .
16.(15分)(I)不能据此判断;
(II)由频率分布直方图可知,成绩90分以下所占比例为 ,因此第85百分
位数一定位于 内,由 ,可以估计该地区近视学生的学习成绩
的第85百分位数约为95.8;
(III)设 “该地区近视学生”, “该地区优秀学生”,
由题设得 , , ,
学科网(北京)股份有限公司所以 .
17.(15分)(I)以 为坐标原点, 的方向为 轴正方向,建立如图所示的空间直角坐标系 ,
不妨设 ,则 , , , , , , ,
, , ,
设平面 的法向量 ,则 ,即 ,可取 ,
因为 ,所以 与平面 所成角的正弦值为 ;
(II)假设截面 内存在点 满足条件,设 , , , ,
所以 , , ,
因为 平面 ,所以 ,所以 ,解得 ,
这与假设矛盾矛盾,所以不存在点 ,使 平面 .
18.(17分)(I)由题设得 ,解得 ,所以 的方程为 ;
(II)由题意可设 ,设 , ,
学科网(北京)股份有限公司由 ,整理得 ,
.
由韦达定理得 , ,
由 得 ,即 ,
整理得 ,因为 ,得 ,解得 或 ,
时,直线 过定点 舍去;
时,满足 ,所以直线 过定点 .
(III)由(II)得直线 ,所以 ,
由 ,整理得 , ,
由题意得 ,
因为 ,所以 ,所以 ,令 , ,
所以 ,在 上单调递减,
所以 的范围是 .
学科网(北京)股份有限公司19.(17分)(I)由题设得 ,所以 ,
又因为 ,所以切点为 ,斜率 ,
所以切线方程为 ,即 ,恒过原点.
(II)由(I)得 ,
① 时, ,
当 时, , 在 上单调递增,
当 时, , 在 上单调递减;
② 时, , 时, , , 在 上单调递增,
时, , 在 上单调递增,在 上单调递减,在
上单调递增;
③ 时, , 在 上单调递增,在 上单调递减;
(III)当 时, ,即 ,
下面证明当 时, , ,即证 ,
令 ,因为 ,所以 ,只需证 ,
即证 ,令 , ,
学科网(北京)股份有限公司,令 , ,
令 , , 与 在 上单调递减,
所以 在 上单调递减, , ,
所以存在 ,使得 ,即 ,
所以 , , , ,
所以 在 上单调递增,在 上单调递减,
所以 , , ,
令 , 时 ,
所以 在 上单调递增,所以 ,
所以 , ,所以 在 上单调递减,
, , , , ,
所以 在 上单调递增,在 上单调递减,
所以 ,综上所述 .
以上各题的其他解法,限于篇幅,从略,请酌情给分.
学科网(北京)股份有限公司