新疆乌鲁木齐地区2024届高三第三次质量监测数学试题_2024年4月_01按日期_30号_2024届新疆乌鲁木齐地区高三下学期第三次质量监测_2024届新疆乌鲁木齐高三下学期三模考试数学试题

乌鲁木齐地区 2024 年高三年级第三次质量监测 数学（问卷） （卷面分值：150 分；考试时间：120 分钟） 注意事项： 1．本试卷分为问卷（4页）和答卷（4页），答案务必书写在答卷（或答题卡）的指定 位置上． 2．答题前，先将答卷密封线内的项目（或答题卡中的相关信息）填写清楚． 第 I 卷（选择题 共 58 分） 一、选择题：本大题共8小题，每小题5分，共计40分．在每小题给出的四个选项中只有一 项是符合题目要求的．请把正确的选项填涂在答题卡相应的位置上． 1．已知集合U1,2,3,4,5，A1,2,3，B2,3,4，则图中阴影部分表示的集合为 A．1 B．1,2 C．1,4 D．1,2,3,4 2．若12i2iabi(a,bR,i是虚数单位），则a，b的值分别等于 A．4,5 B．4,3 C．0,3 D．0,5 3．已知数列a 满足a  1 1  n2,nN* ，若a  3 ，则a  n n a 3 2 1 n1 1 2 A． B． C．1 D．2 2 3 1 1 4．已知 f x lgx ，若a f( )，b f( )，c f(4)，则 2 3 A．abc B．bca C．cab D．cba 5．数列a 是等差数列，S 是数列a 的前n项和，m,n,p,q是正整数，甲：S S S S ， n n n m n p q 乙：mn pq，则甲是乙的 A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 乌鲁木齐地区2024年高三年级第三次质量监测 数学试卷（问卷） 第1页 （共4页） {#{QQABBYqQggAAQoAAARgCUQXCCAAQkACACIoGAAAEIAABSRFABAA=}#}6．三棱锥ABCD中，AD^平面ABC，BAC60，AB1，AC2，AD4，则三 棱锥ABCD外接球的表面积为 A．10 B．20 C．25 D．30 7．直线l ，l 的斜率分别为1, 2，l ，l 夹角为，则sin2 1 2 1 2 3 4 3 3 A． B． C． D． 4 5 5 10 1, x0  8．已知符号函数sgn(x)0, x0，则函数 f(x)sgn(lnx)xlnx零点个数为  1, x0 A．0 B．1 C．2 D．3 二、选择题：本大题共3小题，每小题6分，共计18分．在每小题给出的四个选项中，有多 项符合题目要求．全部选对得6分，部分选对得部分分，有选错的得0分． 9．某运动员的特训成绩分别为：9,12,8,16,12,16,13,20,18,16，则这组数据的 A．极差为12 B．众数为16 C．平均数为14 D．第80百分位数为16 y2 10．已知双曲线x2- =1的右焦点为F，过原点O作斜率为k的直线交双曲线于A，B两 3   点，且FA×FB<0，则k的可能取值是 5 6 A．- B． 2 5 C． 2 D． 3 a+b 11．S={x||x|<1}，S 中的运算“Å”为aÅb= ，则 1+ab A．(-a)Åa=0 B．aÅb=bÅa C． D． 乌鲁木齐地区2024年高三年级第三次质量监测 数学试卷（问卷） 第2页 （共4页） {#{QQABBYqQggAAQoAAARgCUQXCCAAQkACACIoGAAAEIAABSRFABAA=}#}第Ⅱ卷（非选择题 共 92 分） 三、填空题：本大题共3小题，每小题5分，共计15分． 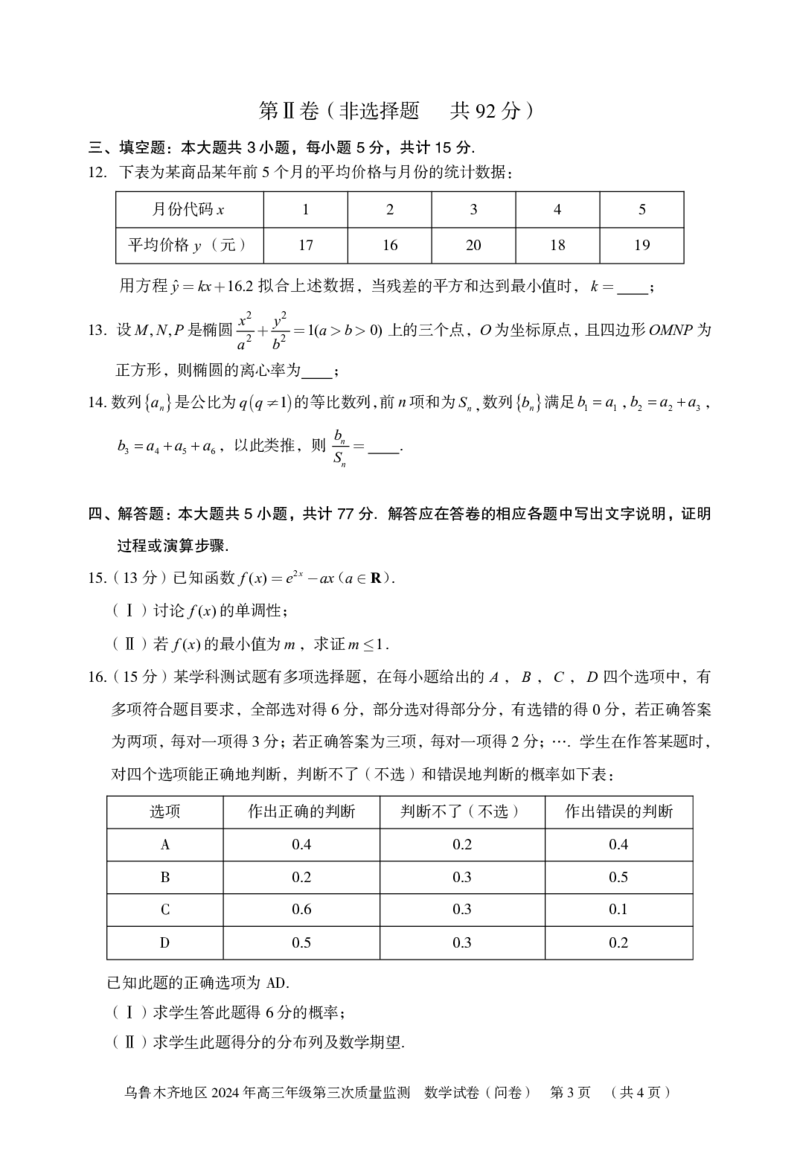12．下表为某商品某年前5个月的平均价格与月份的统计数据： 月份代码x 1 2 3 4 5 平均价格y（元） 17 16 20 18 19 用方程yˆ=kx+16.2拟合上述数据，当残差的平方和达到最小值时，k= ； x2 y2 13．设M,N,P是椭圆 + =1(a>b>0)上的三个点，O为坐标原点，且四边形OMNP为 a2 b2 正方形，则椭圆的离心率为 ； 14．数列a 是公比为q(q¹1)的等比数列，前n项和为S ，数列b 满足b a ，b a a ， n n n 1 1 2 2 3 b b a a a ，以此类推，则 n = ． 3 4 5 6 S n 四、解答题：本大题共5小题，共计77分．解答应在答卷的相应各题中写出文字说明，证明 过程或演算步骤． 15.（13分）已知函数 f(x)=e2x-ax（aÎR）． （Ⅰ）讨论 f(x)的单调性； （Ⅱ）若 f(x)的最小值为m，求证m£1． 16.（15分）某学科测试题有多项选择题，在每小题给出的A，B，C，D四个选项中，有 多项符合题目要求，全部选对得6分，部分选对得部分分，有选错的得0分，若正确答案 为两项，每对一项得3分；若正确答案为三项，每对一项得2分；…．学生在作答某题时， 对四个选项能正确地判断，判断不了（不选）和错误地判断的概率如下表： 选项 作出正确的判断 判断不了（不选） 作出错误的判断 A 0.4 0.2 0.4 B 0.2 0.3 0.5 C 0.6 0.3 0.1 D 0.5 0.3 0.2 已知此题的正确选项为AD． （Ⅰ）求学生答此题得6分的概率； （Ⅱ）求学生此题得分的分布列及数学期望． 乌鲁木齐地区2024年高三年级第三次质量监测 数学试卷（问卷） 第3页 （共4页） {#{QQABBYqQggAAQoAAARgCUQXCCAAQkACACIoGAAAEIAABSRFABAA=}#}17．（15分）直线l与锐角DABC的边AB夹角为，l的方向向量为i，设AB=c，BC=a， CA=b．    （Ⅰ）计算i×(AB+BC+CA)，并由此证明 ccosbcosAacosB； a b （Ⅱ）根据（Ⅰ）证明 = ，c2 =a2+b2-2abcosC ． sinA sinB 18.（17分）由平行六面体ABCD-ABCD 截去三棱锥B -ABC 后得到如图所示的几何体， 1 1 1 1 1 1 1 其体积为5，底面ABCD为菱形，AC与BD交于点O，AB=BC . 1 1 （Ⅰ）证明 DO//平面ABC ； 1 1 1 （Ⅱ）证明 平面DDO^平面ABC ； 1 1 1 （Ⅲ）若AB=2，ÐDAB=60°，AA 与底面ABCD所成角 1 为60°，求AA 与平面ABC 所成角的余弦值． 1 1 1 19.（17分）已知抛物线x2 =4y，DABC的三边AB，AC，BC 所在直线分别与抛物线相切 5 于点M ，N ，D，点A(2,- ). 4 （Ⅰ）求直线MN 的方程； MB AC （Ⅱ）证明 = ； BA CN （Ⅲ）证明 DABC的垂心H 在定直线上. 乌鲁木齐地区2024年高三年级第三次质量监测 数学试卷（问卷） 第4页 （共4页） {#{QQABBYqQggAAQoAAARgCUQXCCAAQkACACIoGAAAEIAABSRFABAA=}#}