数学试卷_2024年2月_01每日更新_16号_2023届重庆缙云教育联盟高三3月质检各科试题及答案全科_2023届重庆缙云教育联盟高三3月质检数学

★秘密·2023年3月16日16：00前 重庆市 2022-2023 学年（下）3 月月度质量检测 高三数学 2023.3 【命题单位：重庆缙云教育联盟】 注意事项： 1.答题前，考生务必用黑色签字笔将自己的姓名、准考证号、座位号在答题卡上填写清楚； 2.每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，在试卷上作答无效； 3.考试结束后，请将本试卷和答题卡一并交回； 4.全卷共6页，满分150分，考试时间120分钟。 一、选择题：本题共8小题，每小题5分，共40 分。在每小题给出的四个选项中，只有一项 是符合题目要求的。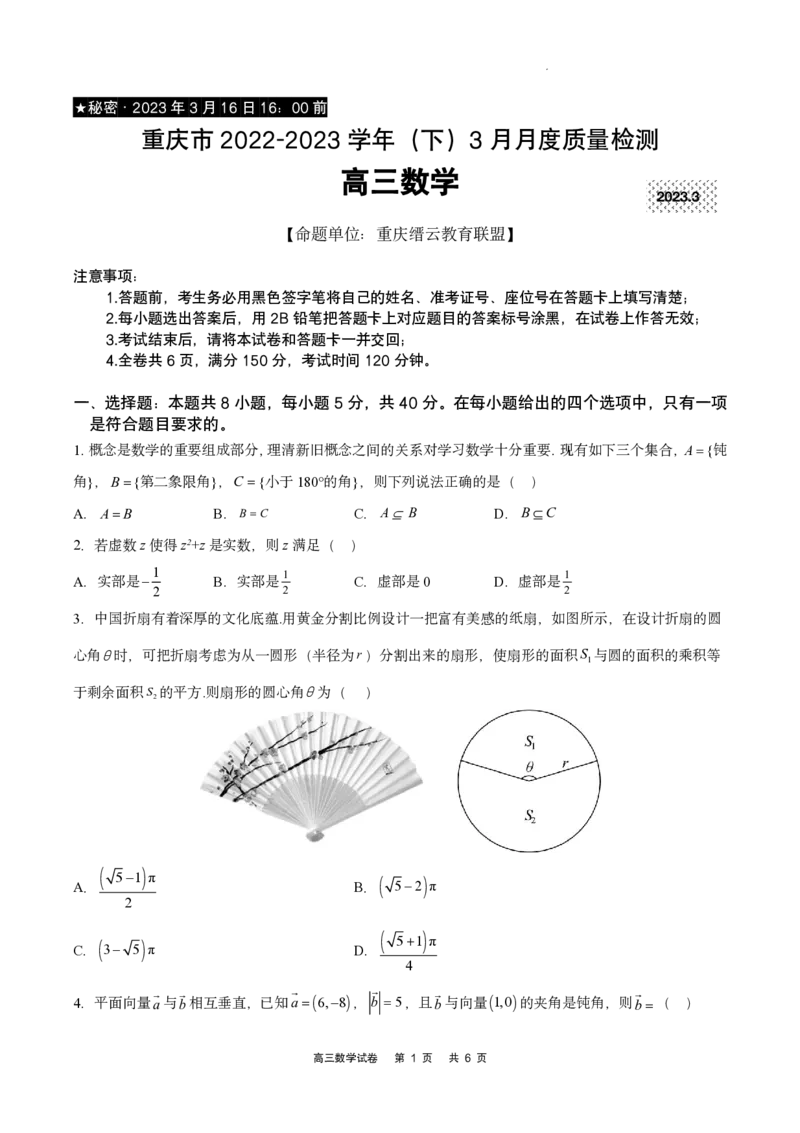 1．概念是数学的重要组成部分，理清新旧概念之间的关系对学习数学十分重要．现有如下三个集合，A{钝 角}，B{第二象限角}，C{小于180°的角}，则下列说法正确的是（ ） A．AB B．BC C．AB D．BC 2．若虚数z使得z2+z是实数，则z满足（ ） 1 1 1 A．实部是 B．实部是 C．虚部是0 D．虚部是 2 2 2 3．中国折扇有着深厚的文化底蕴.用黄金分割比例设计一把富有美感的纸扇，如图所示，在设计折扇的圆 心角时，可把折扇考虑为从一圆形（半径为r）分割出来的扇形，使扇形的面积S 与圆的面积的乘积等 1 于剩余面积S 的平方.则扇形的圆心角为（ ） 2   51 π   A． B． 52 π 2     51 π C． 3 5 π D． 4       4．平面向量a与b相互垂直，已知a6,8 ， b 5，且b与向量 1,0 的夹角是钝角，则b（ ） 高三数学试卷 第 1 页 共 6 页 学科网（北京）股份有限公司A． 3,4 B． 4,3 C． 4,3 D． 4,3 5．已知点 a,b 的横纵坐标均是集合N 2,3,4,0,5,6 中的元素，若点 a,b 在第二象限内的情况共有n n  2 种，则 x   的展开式中的第5项为（ ）  x A．240x3 B．80x3 C．  9 D．  9 192x 2 400x 2 6．设xy x y xy ,xΔy x y xy ，若正实数a b,c,d 高三数学试卷 第 2 页 共 6 页 学科网（北京）股份有限公司 , aΔbcΔd  满足：acbd,则下列选项一定正确的  bΔcad 是（ ） A．db B．bc C．bΔca D．dca sin2x π   7．函数 f x 0 x ，设球O的半径为 f xcosx ，则（ ） esin2x  2  4 A．球O的表面积随x增大而增大 B．球O的体积随x增大而减小 4 4 C．球O的表面积最小值为 D．球O的体积最大值为 e2 3e3 8．设a2e0.1,b2ln1.21,则（ ） A．a1.8,1.81,b1.8,1.81 B．a1.8,1.81,b1.8,1.81 C．a1.8,1.81,b1.8,1.81 D．a1.8,1.81,b1.8,1.81 二、多项选择题：本题共4小题，每小题5分，共20 分。在每小题给出的选项中，有多项符 合题目要求的。全部选对的得5分，部分选对的得2 分，有选错的得2 分。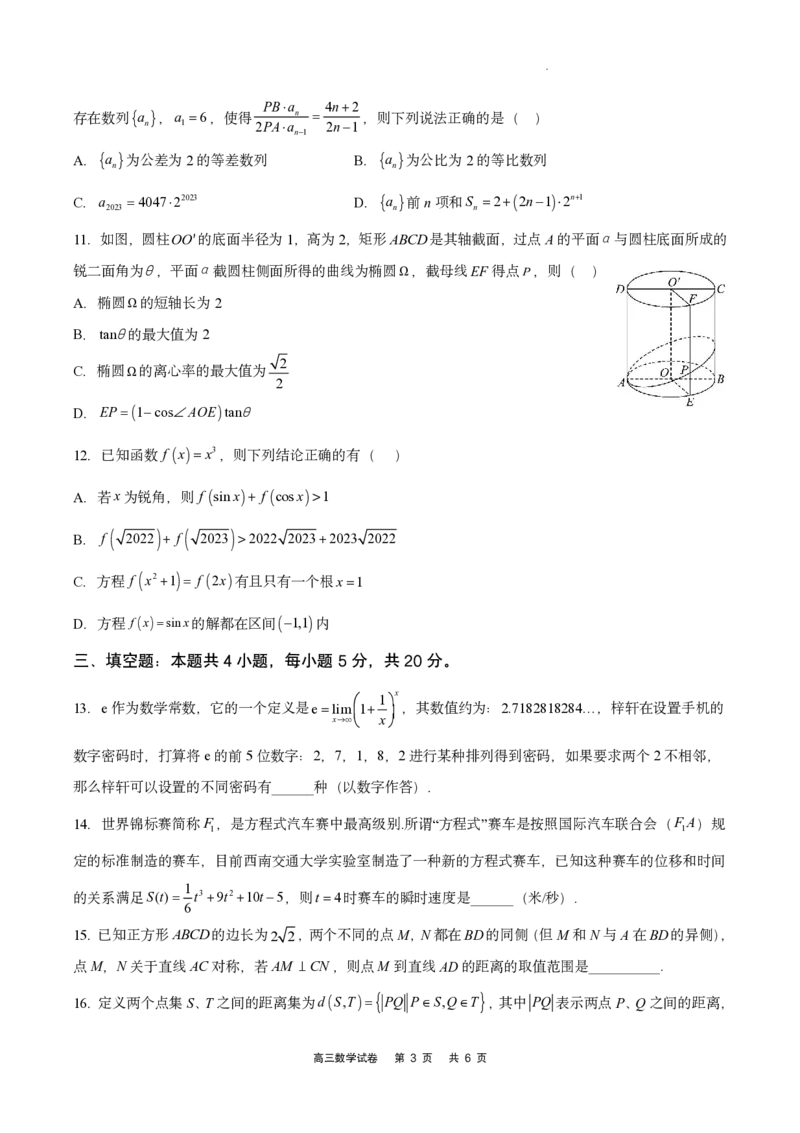 9．记无理数3.14159260288小数点后第a位上的数字是b，则b是a的函数，记作b f a ，定义 域为A，值域为B，其下列说法正确的是（ ） A．值域B是定义域A的子集 B．函数图像 f a 是一群孤立的点 C． f 62 D．a也是b的函数，记作a f b 2 10．在平面直角坐标系xOy中，A为坐标原点，B2,0 ，点列P在圆  x 2   y2  16 上，若对于nN*，  3 9PBa 4n2 存在数列 a  ，a 6，使得 n  ，则下列说法正确的是（ ） n 1 2PAa 2n1 n1 A． a  为公差为2的等差数列 B． a  为公比为2的等比数列 n n C．a 404722023 D． a  前n项和S 22n12n1 2023 n n 11．如图，圆柱OO的底面半径为1，高为2，矩形ABCD是其轴截面，过点A的平面与圆柱底面所成的 锐二面角为，平面截圆柱侧面所得的曲线为椭圆Ω，截母线EF得点P，则（ ） A．椭圆Ω的短轴长为2 B．tan的最大值为2 2 C．椭圆Ω的离心率的最大值为 2 D．EP1cosAOEtan 12．已知函数 f xx3 ，则下列结论正确的有（ ） A．若x为锐角，则 f sinx f cosx1     B． f 2022  f 2023 2022 20232023 2022 C．方程 f  x21   f 2x 有且只有一个根x1 D．方程 fxsinx的解都在区间 1,1 内 三、填空题：本题共4小题，每小题5 分，共20 分。 x  1 13．e作为数学常数，它的一个定义是elim1  ，其数值约为：2.7182818284…，梓轩在设置手机的 x x 数字密码时，打算将e的前5位数字：2，7，1，8，2进行某种排列得到密码，如果要求两个2不相邻， 那么梓轩可以设置的不同密码有______种（以数字作答）． 14．世界锦标赛简称F，是方程式汽车赛中最高级别.所谓“方程式”赛车是按照国际汽车联合会（FA）规 1 1 定的标准制造的赛车，目前西南交通大学实验室制造了一种新的方程式赛车，已知这种赛车的位移和时间 1 的关系满足S(t) t39t210t5，则t4时赛车的瞬时速度是______（米/秒）. 6 15．已知正方形ABCD的边长为2 2，两个不同的点M，N都在BD的同侧（但M和N与A在BD的异侧）， 点M，N关于直线AC对称，若AM CN，则点M 到直线AD的距离的取值范围是__________. 16．定义两个点集S、T之间的距离集为dS,T  PQ PS,QT  ，其中 PQ 表示两点P、Q之间的距离， 高三数学试卷 第 3 页 共 6 页 学科网（北京）股份有限公司已知k、tR，S  x,y ykxt,xR  ，T   x,y y 4x21,xR  ，若dS,T1, ，则t的值 为______. 四、解答题：本题共6小题，共70 分。解答应写出文字说明、证明过程或演算步骤。 17．篮球诞生美国马萨诸塞州的春田学院．1891年，春田学院的体育教师加拿大人詹姆斯奈史密斯博士 （JamesNaismith）为了对付冬季寒冷的气温，让学生们能够在室内有限的空间里继续进行有趣的传球训 练．现有甲、乙、丙3名同学在某次传球的训练中，球从甲开始，等可能地随机传向另外2人中的1人， 接球者接到球后再等可能地随机传向另外2人中的1人，如此不停地传下去，假设传出的球都能接住．记 第n次传球之前球在甲手里的概率为pn，第n次传球之前球在乙手里的概率为qn，显然p =1，q =0． 1 1 (1)求p ＋2q 的值； 3 3 (2)比较p ，q 的大小． 8 8 18．悬索桥（如图）的外观大漂亮，悬索的形状是平面几何 中的悬链线.1691年莱布尼兹和伯努利推导出某链线的方程 c x x 为y ec ec，其中c为参数.当c1时，该方程就是双 2  exex 曲余弦函数coshx ，类似的我们有双曲正弦函数 2 ex ex sinhx . 2 (1)从下列三个结论中选择一个进行证明，并求函数 ycosh2xsinhx 的最小值； ① coshx  2  sinhx  2 1； ②sinh2x2sinhxcoshx ； ③cosh2x coshx  2  sinhx  2 . 高三数学试卷 第 4 页 共 6 页 学科网（北京）股份有限公司  (2)求证：x  , ，coshcosxsinhsinx .  4 19．数据显示，中国在线直播用户规模及在线直播购物规模近几年都保持高速增长态势，下表为2017-2021 年中国在线直播用户规模（单位：亿人），其中2017年-2021年对应的代码依次为1-5. 年份代码x 1 2 3 4 5 市场规模y 3.98 4.56 5.04 5.86 6.36 (1)由上表数据可知，可用函数模型  yb  xa  拟合y与x的关系，请建立y关于x的回归方程（a ，b  的 值精确到0.01）； (2)已知中国在线直播购物用户选择在品牌官方直播间购物与不在品牌官方直播间购物的人数之比为4：1， 按照分层抽样从这两类用户中抽取5人，再从这5人中随机抽取2人，求这2人全是选择在品牌官方直播 间购物用户的概率. 5 参考数据：y5.16，v1.68， v y 45.10，其中v  x . i i i i i1 参考公式：对于一组数据 v,y  ， v ,y  ，…， v ,y  ，其回归直线  yb  va  的斜率和截距的最小二乘 1 1 2 2 n n n v y nvy i i 估计公式分别为b   i1 ，a   yb  v. n v2nv 2 i i1 20．如图，边长是6的等边三角形ABC和矩形BCDE.现 以BC为轴将面ABC进行旋转，使之形成四棱锥 A BCDE，O是等边三角形ABC的中心，M ，N 分别 1 是BC，DE的中点，且AB2ON ，OF//面BCDE，交AC 1 1 于F. (1)求证OF 面AMN 1 (2)求DF和面A 1 MN所成角的正弦值. 高三数学试卷 第 5 页 共 6 页 学科网（北京）股份有限公司 p  8 21．已知点F ,0到直线l :3x4y110的距离等于 ，其中0 p10．设平面内与点F和直线  2  1 5 p l :x 距离相等的点的轨迹为C． 2 2 (1)求C的方程； (2)设l 与C在第一象限的交点为A，l 与x轴的交点为B，求△ABF的面积． 1 2 22．俄国数学家切比雪夫（П.Л.Чебышев，1821-1894）是研究直线逼近函数理论的先驱.对定义在非空集合 I 上的函数 f x ，以及函数gxkxbk,bR ，切比雪夫将函数y f xgx ，xI的最大值称为 函数 f x 与gx 的“偏差”. (1)若 f x x2 x0,1 ，gxx1，求函数 f x 与gx 的“偏差”； (2)若 f x x2 x1,1 ，gx xb，求实数b，使得函数 f x 与gx 的“偏差”取得最小值. 高三数学试卷 第 6 页 共 6 页 学科网（北京）股份有限公司