数学试题答案_2024年5月_01按日期_30号_2024届重庆市巴蜀中学高三5月适应性月考卷（十）_重庆市巴蜀中学2024届高三年级下学期5月适应性月考卷（十）数学

数学参考答案
一、单项选择题（本大题共8小题，每小题5分，共40分）
题号 1 2 3 4 5 6 7 8
答案 C A C B B D B B
【解析】
1．由于x2 4x30，解得1x3，又因为AB且B{x|1xa}，所以a≥3，故选C．
   
2．因为“a∥b，所以2x2 18，解得x3，所以“x3”是“a∥b”的充分不必要条件，
故选A．
3．因为S 15a 60，所以a 4，所以a a 2a 8，故选C．
15 8 8 3 13 8
4．按照3原则可知：488≤5003，解得：≤4，所以的最大值为4，故选B．
5．第一种情况：当丙为第一名时，有A3 6种；第二种情况：当丁为第一名时，有A3 6种；
3 3
第三种情况：当戊为第一名时，有A3A2 12种，所以共有：661224种，故选B．
3 2
1 1
6．设直线l与曲线yln(xa)的切点为P(x，y )，由y[ln(xa)] ，则 1，
0 0 xa x a
0
则x 1a，y 0，即切点为P(1a，0) ，所以直线 l 为 yx1a ．又直线 l 与圆
0 0
|1a|
x2  y2 2都相切，则有  2，解得a3或a1，故选D．
2
1
7．设二面角PEF C的平面角为，则coscos60 ． 因为PC⊥平面ABC，过点P
2
作截面分别交 AC，BC 于点 E，F，所以△PEF 在平面 EFC 上的投影为△CEF ，所以
S 1 1
△CEF cos ，即S 2S ．设CE x，CF  y ，则S  xy，过点 P 作
S 2 △PEF △CEF △CEF 2
△PEF
PC
PM⊥EF 于点 M ，连接 CM ，则∠PMC60 ，所以 tan60 3 ，所以
CM
2 3 2 3 2 3
CM  ，在△CEF 中，由等面积得：xyEFCM  x2  y2  ≥ 2xy，解
3 3 3
8 8 4
得：xy≥ ，当且仅当x y时，等号成立，所以xy的最小值为 ，所以(S )  ，
3 3 △CEF min 3
8
所以(S ) 2(S )  ，故选B．
△PEF min △CEF min 3
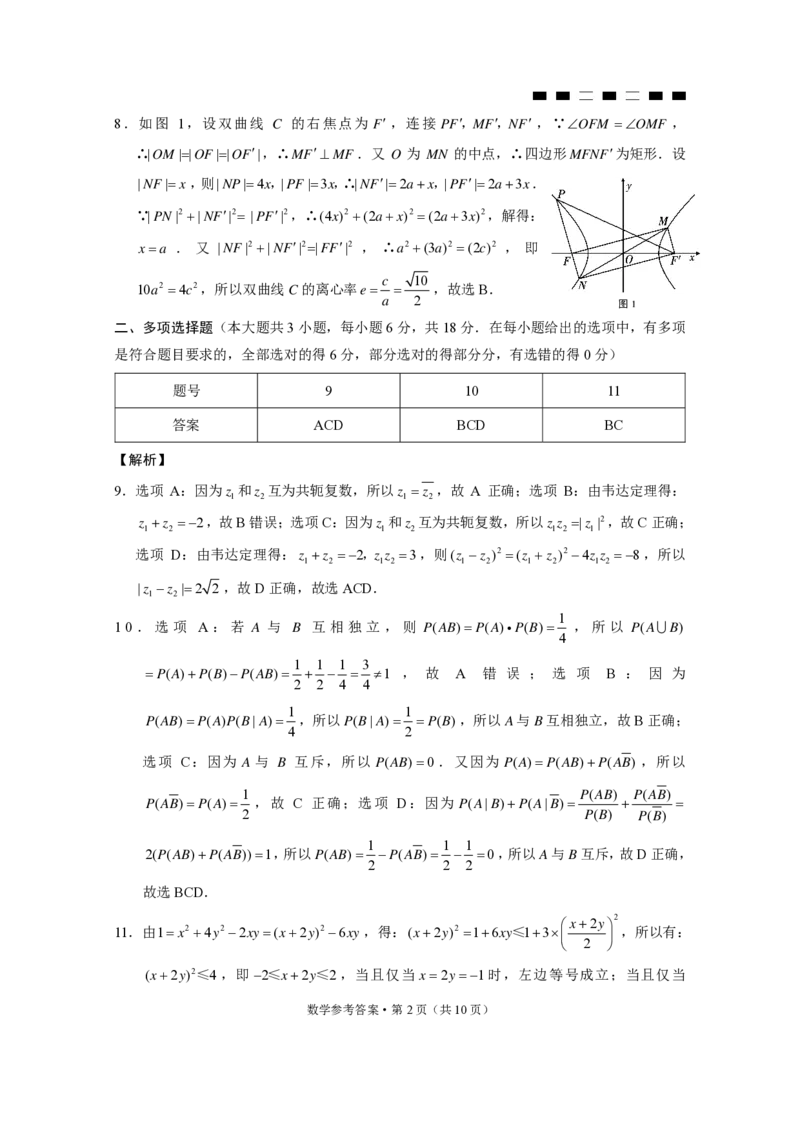
数学参考答案·第1页（共10页）8．如图 1，设双曲线 C 的右焦点为 F ，连接 PF，MF，NF ，∵OFM OMF ，
∴|OM ||OF||OF|，∴MFMF．又 O 为 MN 的中点，∴四边形MFNF为矩形．设
|NF|x，则|NP|4x，|PF|3x，∴|NF|2ax，|PF|2a3x．
∵|PN|2 |NF|2 |PF|2，∴(4x)2 (2ax)2 (2a3x)2，解得：
xa ． 又 |NF|2 |NF|2|FF|2 ， ∴a2 (3a)2 (2c)2 ， 即
c 10
10a2 4c2，所以双曲线C的离心率e  ，故选B．
a 2
图1
二、多项选择题（本大题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项
是符合题目要求的，全部选对的得6分，部分选对的得部分分，有选错的得0分）
题号 9 10 11
答案 ACD BCD BC
【解析】
9．选项 A：因为z 和z 互为共轭复数，所以z z ，故 A 正确；选项 B：由韦达定理得：
1 2 1 2
z z 2，故B错误；选项C：因为z 和z 互为共轭复数，所以z z |z |2，故C正确；
1 2 1 2 1 2 1
选项 D：由韦达定理得：z z 2，z z 3，则(z z )2 (z z )2 4z z 8，所以
1 2 1 2 1 2 1 2 1 2
|z z |2 2 ，故D正确，故选ACD．
1 2
1
10 ．选项 A：若 A 与 B 互相独立，则 P(AB)P(A)P(B) ，所 以 P(AB)
4
1 1 1 3
P(A)P(B)P(AB)    1 ， 故 A 错 误 ； 选 项 B ： 因 为
2 2 4 4
1 1
P(AB)P(A)P(B|A) ，所以P(B|A) P(B)，所以A与B互相独立，故B正确；
4 2
选项 C：因为 A与 B 互斥，所以 P(AB)0 ．又因为 P(A)P(AB)P(AB) ，所以
1 P(AB) P(AB)
P(AB)P(A) ，故 C 正确；选项 D：因为 P(A|B)P(A|B)  
2 P(B) P(B)
1 1 1
2(P(AB)P(AB))1，所以P(AB) P(AB)  0，所以A与B互斥，故D正确，
2 2 2
故选BCD．
x2y 2
11．由1x2 4y2 2xy(x2y)2 6xy，得：(x2y)2 16xy≤13

，所以有：
 2 
(x2y)2≤4 ，即2≤x2y≤2，当且仅当 x2y1时，左边等号成立；当且仅当
数学参考答案·第2页（共10页）x2 4y2
x2y1时，右边等号成立，故A错误，B正确；又因为x2 4y2 12xy≤1 ，
2
所以有x2 4y2≤2，当且仅当x2y1或x2y1时，等号成立，故C正确；又因为
x2 4y2 2
x2 4y2 12xy≥1 ， 所 以 有 x2 4y2≥ ， 当 且 仅 当
2 3
3 3 3 3
x ，2y 或x ，2y 时，等号成立，故D错误，故选BC．
3 3 3 3
【注】本题也可以通过三角换元进行求解．
三、填空题（本大题共3小题，每小题5分，共15分）
题号 12 13 14
5π 3
答案 8或9 4；
3 2
【解析】
12．由题可知：击中目标的次数X ~ B(14，0.6)，因为(n1)p(141)0.69，所以由二项
分布的性质可知：最有可能击中目标8次或9次．
【参照人教A版选择性必修3学生用书第82页】
【注】也可直接通过比较概率大小而求值．
π  π π
13．因为 f(x)的一个对称中心为  ，0 ，所以有2 kπ，k Z，即 kπ，k Z
6  6 1 1 3 1 1
 π  2π   π π 
①．又因为 f(x)在   0， 3   上单增，所以有   ， 3       2 2k 2 π， 2 2k 2 π   ，k 2 Z，
 π
≥ 2k π，
  2 2 π π
即 得到 2k π≤≤ 2k π，k Z②．又因为0，所以结
2π π 2 2 6 2 2
 ≤ 2k π，
 3 2 2
5π
合①②知：的最小值为 ．
3
14．延长 AF 交抛物线 E 于点 D，连接 CD，过点 A 作AH⊥x轴于点 H，由抛物线的性质结
论可知：直线 CA 与 CD 关于 x 轴对称． 又因为 BF 为∠AFC的角平分线，所以
∠AFB∠CFB∠CFD60 ， 所 以 ∠AFH 60 ， 由 焦 半 径 公 式 得 ：
p 2
|AF|  4 ；则 AH 2 3，FH 2 ．又因为 F(1，0) ，所以
1cos∠AFH 1cos60
数学参考答案·第3页（共10页）2 30 3
A(3，2 3)或 A(3，2 3)． 又因为C(1，0) ，所以直线 l 的斜率k   或
3(1) 2
2 30 3 3
k   ，所以直线l的斜率为 ．
3(1) 2 2
【注】直接设直线l的方程为xmy1，与抛物线E：y2 4x联立方程，利用韦达定理以
及角平分线性质，也可以求解．
四、解答题（共77分．解答应写出文字说明，证明过程或演算步骤）
15．（本小题满分13分）
（1）证明：如图2，取BC的中点E，连接BE，AE，则AE⊥BC．
1
又因为ABCABC 为正三棱柱，所以平面ABC⊥平面BBCC ．
1 1 1 1 1
又因为BC平面ABC平面BBCC ，所以AE⊥平面BBCC ．
1 1 1 1
又因为BC 平面BBCC ，所以AE⊥BC ．…………………………………………（2分）
1 1 1 1
又因为AB2，BB  2，
1
BE 2 BB 2
所以tan∠EBB  ，tan∠BCB 1  ，
1 BB 2 1 1 BC 2
1 1 1
所以tan∠EBBtan∠BCB，所以∠EBB∠BCB．
1 1 1 1 1 1
又因为∠BCB∠BBC 90，
1 1 1 1 图2
所以BE⊥BC ． ………………………………………………………………………（5分）
1 1
又因为AEBEE，所以BC ⊥平面ABE，
1 1 1
所以AB ⊥BC ． ………………………………………………………………………（6分）
1 1
（2）解：过点D作DF⊥BC 于点F，
由（1）知：AE⊥平面BBCC ，所以DF⊥平面BBCC ．
1 1 1 1
又因为D为边AC的中点，所以AE2DF．
3
因为AB2且△ABC为正三角形，所以AE 3，所以DF  ．
2
1
又因为S  2 2  2，
△BCC1 2
1 1 3 6
所以V  S DF   2  ．……………………………………（9分）
DBCC1 3 △BCC1 3 2 6
（3）解：过点F作FG⊥BC 于点G，连接DG，
1
因为DF⊥平面BBCC 且FG⊥BC ，
1 1 1
数学参考答案·第4页（共10页）所以∠DGF 即为二面角DBC C的平面角．……………………………………（10分）
1
GF 3 3
又因为sin∠FBG  且BF  ，
BF 3 2
3 DF
所以GF  ，所以tan∠DGF  1．…………………………………………（12分）
2 GF
π
又因为∠DGF 为锐角，所以∠DGF  ，
4
π
即二面角DBC C的大小为 ．……………………………………………………（13分）
1 4
16．（本小题满分15分）
解：（1）如下表：
疾病
药物 合计
未患病 患病
未服用 50 40 90
服用 75 35 110
合计 125 75 200
………………………………………………………………………………………（3分）
（2）零假设为H ：药物与患病独立，即药物对疾病没有效果．
0
根据列联表中的数据，经计算得到：
200(50354075)2
2  3.3672.706 x ，…………………………………（5分）
1257590110 0.1
所以依据0.1的独立性检验，我们可以推断H 不成立，即认为药物对预防疾病有效，
0
该推断犯错误的概率不超过0.1．………………………………………………………（7分）
5 4
结论解释：未服用药物中未患病和患病的频率分别为 和 ，服用药物中未患病和患病的
9 9
15 7
频率分别为 和 ，根据频率稳定于概率的原理，可以推断服用药物不患病的概率更
22 22
大．【参照人教A版选择性必修3教师用书第176页】
………………………………………………………………………………………（9分）
（3）按分层抽样的方法从未患病动物中抽取10只，则未服用药物的动物有4只，服用药
物的动物有6只，所以X的可能取值为0，1，2，3，4，…………………………（11分）
数学参考答案·第5页（共10页）C4 15 C3C1 80 C2C2 90
则P(X 0) 6  ，P(X 1) 6 4  ，P(X 2) 6 4  ，
C4 210 C4 210 C4 210
10 10 10
C1C3 24 C4 1
P(X 3) 6 4  ，P(X 4) 4  ，
C4 210 C4 210
10 10
所以X的分布列如下：
X 0 1 2 3 4
15 80 90 24 1
P
210 210 210 210 210
……………………………………………………………………………………（14分）
15 80 90 24 1
则E(X)0 1 2 3 4 1.6．……………………（15分）
210 210 210 210 210
17．（本小题满分15分）
3sinC
解：（1）由正弦定理得： sinBtanAcosB，
sinA
3sinC sinB sinA
所以   ，………………………………………………………（2分）
sinAcosB cosB cosA
3sinC sinA sinB sinAcosBcosAsinB sin(AB) sinC
所以      ，
sinAcosB cosA cosB cosAcosB cosAcosB cosAcosB
sinA
化简得：  3，所以tanA 3．………………………………………………（5分）
cosA
π
又因为A(0，π)，所以A ．………………………………………………………（6分）
3
a b c 2 6
（2）由正弦定理得：    4 2，
sinA sinB sinC π
sin
3
所以b4 2sinB，c4 2sinC，………………………………………………………（8分）
1 2π 
所以S
△ABC

2
bcsinA8 3sinBsinC 8 3sinBsin
 3
B

 2π  2π  2π
4 3  cos cos2B  4 3cos2B 2 3．
 3  3   3 
……………………………………………………………………………………（11分）
数学参考答案·第6页（共10页） π  π
0B ， 0B ，
 
 2  2
又因为△ABC为锐角三角形，所以 所以
2π π π 2π
0 B ，  B ，
 3 2 6 3
π π 2π  π π
所以B ，  ，所以2B  ，  ，………………………………………（13分）
6 2 3  3 3
 2π 1 
所以cos2B  ，1

，
 3  2 
 2π
所以S △ABC 4 3cos  2B 3   2 3(4 3，6 3]．…………………………………（15分）
【另注】第（2）问也可以用几何意义说明：
π
由于A 且a2 6，
3
所以点A的轨迹为△ABC外接圆O的一部分，即弦BC所对的优弧．
当AO⊥BC时，此时△ABC的面积最大为6 3；
当AB⊥BC或AC⊥BC时，此时△ABC的面积最小为4 3；
由于△ABC为锐角三角形，所以取不到最小值；
因此S (4 3，6 3]． 也可根据实际情况酌情给分．
△ABC
18．（本小题满分17分）
c 1
 ，

a 2

 3 2
 12  2   a2，
（1）解：由题可知：  1，解得
 a2 b2 b 3，
a2 b2 c2，




x2 y2
所以C的方程为  1．
4 3
………………………………………………………………………………………（4分）
（2）（ⅰ）证明：①当直线l的斜率为0时，则不妨设P(2，0)，Q(2，0)，
3 3
2 2
所以k k   1为定值．…………………………………………………（5分）
1 2 12 12
数学参考答案·第7页（共10页）②当直线l的斜率不为0时，设直线l：xmy4(m0)，P(x，y )，Q(x，y )，
1 1 2 2
xmy4，
联立直线l与椭圆C的方程：
3x2 4y2 12，
消掉x得：3(my4)2 4y2 12，
化简得：(3m2 4)y2 24my360，
 24m
y  y  ，
  1 2 3m2 4
当0时，由韦达定理得： ……………………………………（7分）
36
y y  ，
 1 2 3m2 4
3
所以my y  (y  y )，
1 2 2 1 2
3 3  3  3
y  y  y  (x 1)y  (x 1)
1 2 2 2  1 2 2  2 2 1
所以k k   
1 2 x 1 x 1 (x 1)(x 1)
1 2 1 2
 3  3  3 
y  (my 3)y  (my 3) 2my y 3 m(y  y )9
 1 2 2  2 2 1 1 2  2  1 2
 
(my 3)(my 3) m2y y 3m(y  y )9
1 2 1 2 1 2
 3  3
3(y  y )3 m(y  y )9  m(y  y )9
1 2  2  1 2 2 1 2
  1为定值，
3 3
 m(y  y )3m(y  y )9 m(y  y )9
2 1 2 1 2 2 1 2
综上：k k 1为定值．……………………………………………………………（11分）
1 2
x x，
 N 1
（ⅱ）证明：设线段PM的中点为N(x ，y )，M(x，y )，易得 y  y
N N 1 M y  1 M ，

 N 2
……………………………………………………………………………………（12分）
3 3
由题可得：直线AQ的方程为yk (x1) ，则y k (x 1) ，
2 2 M 2 1 2
3
直线AP的方程为yk (x1) ，
1 2
3
则y k (x 1) ，…………………………………………………………………（13分）
1 1 1 2
y  y 1 3 3 1 3
所以y  1 M  k (x 1) k (x 1)  (k k )(x 1) ．
N 2 2   1 1 2 2 1 2   2 1 2 1 2
……………………………………………………………………………………（15分）
数学参考答案·第8页（共10页）y  y 1 3 1
由（ⅰ）知：k k 1，所以y  1 M  (x 1)  x 2．
1 2 N 2 2 1 2 2 N
1
又因为直线AT 的方程为y x2，所以点N(x ，y )在直线AT上，
2 N N
即直线AT过线段PM的中点．…………………………………………………………（17分）
19．（本小题满分17分）
证明：（1）令 f(x)xsinx(x0)，则 f(x)1cosx≥0，
所以 f(x)在(0，)上单增，所以 f(x) f(0)0，即xsinx．
………………………………………………………………………………………（2分）
x3 x2
再令g(x)x sinx(x0)， 则g(x)1 cosx且g(0)0，
6 2
再求导得：g(x)xsinx0，
所以g(x)在(0，)上单减，所以g(x)g(0)0，
x3
所以g(x)在(0，)上单减，所以g(x)g(0)0，即x sinx．
6
x3
综上：当x0时，x sinxx成立，证毕．……………………………………（5分）
6
sina
（2）（ⅰ）由于a a  n ，所以(n1)a (n1)a sina ，
n1 n n1 n1 n n
所以(n1)a na a sina ．………………………………………………………（7分）
n1 n n n
由（1）知：当a 0时，a sina 0，
n n n
所以(n1)a na a sina 0，所以{na }为递增数列，证毕．
n1 n n n n
………………………………………………………………………………………（8分）
3a 1 3a2 1 a 1 1 a
（ⅱ）要证na  1 ，即证  1   1    1 ．
n 3a2 na 3a a 3 a na 3
1 n 1 1 1 n
………………………………………………………………………………………（9分）
a3
由（1）知：当a 0时，a sina  n ，
n n n 6
a3
所以(n1)a na a sina  n ，………………………………………………（10分）
n1 n n n 6
a3 1 1 a2
即有(n1)a na  n ，所以   n ，
n1 n 6 na (n1)a 6n(n1)a
n n1 n1
数学参考答案·第9页（共10页）1 1 a2
所以   n ．…………………………………………………（12分）
na (n1)a 6n(n1)a
n n1 n1
又因为0a  3，所以sina 0，
1 1
sina
所以a a  1 a  3，归纳易得：数列{a }为递减数列．
2 1 2 1 n
……………………………………………………………………………………（13分）
又因为数列{na }为递增数列，
n
1 1 a2 a2 a
所以   n  n  1 ，
na (n1)a 6n(n1)a 6n(na ) 6n2
n n1 n1 n
1 1  1 1   1 1  1 1 a  1 1 1 
所以         1     ．
a na a 2a  2a 3a  (n1)a na 6 12 22 n2 
1 n 1 2 2 3 n1 n
……………………………………………………………………………………（15分）
1 1 1 1
又因为    (n≥2)，
n2 n(n1) n1 n
1 1 1 1 1 1 1
所以   11   2 2，
12 22 n2 2 n1 n n
1 1 a  1 1 1  a 3a
所以   1     1 ，即na  1 ，证毕．
a na 6 12 22 n2  3 n 3a2
1 n 1
……………………………………………………………………………………（17分）
数学参考答案·第10页（共10页）