数学高三答案_2024年3月_013月合集_2024届江西省南昌市HGT高三第一次模拟考试_2024届江西省南昌市HGT高三第一次模拟考试-数学

2024年HGT第一次模拟测试 数学 参考答案及评分意见 一、单项选择题：共8小题，每题5分，共40分．在每小题给出的四个选项中，只有一个 选项是符合题目要求的． 题号 1 2 3 4 5 6 7 8 答案 C B C A A D B C 二、多项选择题：共4小题，每题5分，共20分．在每小题给出的四个选项中，有多项符 合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分． 题号 9 10 11 12 答案 BC ABD ACD ACD 三、填空题：共4小题，每小题5分，共20分. 1 5 13． 14．160 15．[0,80 3] 16． 6 3 四、解答题：共6小题，共70分．解答应写出文字说明、证明过程或演算步骤． 2e 17．【解析】（1） f(x)1ln2lnxln ， ……………… 2分 x 2e 令 f(x)0，得0 1，即x2e， ……………… 4分 x 所以 f(x)的单调递减区间为(2e,). ……………… 5分 （2）当x(0,2e)时, f(x)0, f(x)单调递增； 当x(2e,)时, f(x)0, f(x)单调递减， ……………… 8分 所以 f(x) f(2e)2e，即 f(x)的最大值为2e. ……………… 10分 a b 18．【解析】由题意知 n1  n2 ， ……………… 2分 a b n n a （1）因为b 1，且{b }是公比为2的等比数列，所以 n1 4， 1 n a n 因为a 1，所以数列{a }首项为1，公比为4的等比数列， ……………… 4分 1 n 1(14n) 1 所以S   (4n 1)； ……………… 6分 n 14 3 （2）因为b 1，且{b }是公差为2的等差数列，所以b 2n1， 1 n n a b 2n3 所以 n1  n2  ， ……………… 8分 a b 2n1 n n a 2n1 a 2n1 a 5 所以 n  ， n1  ，……， 2  ， ……………… 10分 a 2n3 a 2n5 a 1 n1 n2 1 a (2n1)(2n1) 1 所以 n  ，因为a 1，所以a  (4n2 1). a 31 1 n 3 1 ……………… 12分 — 高三 数学 第 页（共 页）— 1 51 19．【解析】（1）由已知，AB ACcosBAC 10 5， 2 2 AD ACcosDAC 10 5 2， ……………… 2分 2 因为BADBACDAC 6045， 1 2 3 2 2 6 所以cosBADcos60ocos45o sin60osin45o      ， 2 2 2 2 4 ……………… 4分 所以在ABD中，BD2  AB2 AD22ABADcosBAD 2 6 2550255 2 4 5025 3. ……………… 6分 6 2 （2）【解法1】因为sinBADsin(6045) ， …………… 8分 4 又因为S S S ， ABD ABE ADE 1 1 1 所以 ABADsinBAD ABAEsinBAE AEADsinEAD， 2 2 2 ……………… 10分 1 6 2 1 3 1 2 即 55 2  5AE  AE5 2 ， 2 4 2 2 2 2 解得AE 5 35. ……………… 12分 1 ABADsinBAD AE S 2 3 【解法2】因为  ABD   ， ………… 9分 EC S 1 3 BCD BCCDsinBCD 2 又因为AC 10，所以AEEC 10，则AE 3AE 10， 所以AE 5 35. ……………… 12分 20. 【解析】（1）记投资期间经济形势好为事件B ，投资期间经济形势不好为事件B ， 1 2 投资咨询公司预测投资期间经济形势好为事件A， 则P(B )0.4,P(B )0.6， ……………… 2分 1 2 因此P(A)P(B AB A)0.40.80.60.30.5； ……………… 5分 1 2 —高三 数学 第 页（共 页）— 2 5（2）若采取方案一，则该公司获得的利润值X 万元的分布列是 X 50 20 P 0.4 0.6 EX 500.4200.68万元； ……………… 7分 若采取方案二：设该公司获得的利润值为Y万元，有以下情况， 投资期间经济形势好，咨询公司乙预测经济形势为好，Y 49.5， 其发生的概率为：P(B A)0.40.80.32， 1 投资期间经济形势好，咨询公司乙预测经济形势为不好，Y 1.5， 其发生的概率为：P(B A)0.40.20.08， 1 投资期间经济形势不好，咨询公司乙预测经济形势为好，Y 20.5， 其发生的概率为：P(B A)0.60.30.18， 2 投资期间经济形势不好，咨询公司乙预测经济形势为不好，Y 1.5， 其发生的概率为：P(B A)0.60.70.42， ……………… 9分 2 因此，随机变量Y的分布列为： Y 20.5 1.5 49.5 P 0.18 0.5 0.32 因此，EY 20.50.181.50.549.50.32 3.690.7515.8411.4万元， 因为EX EY ，所以甲公司应该选择方案二. 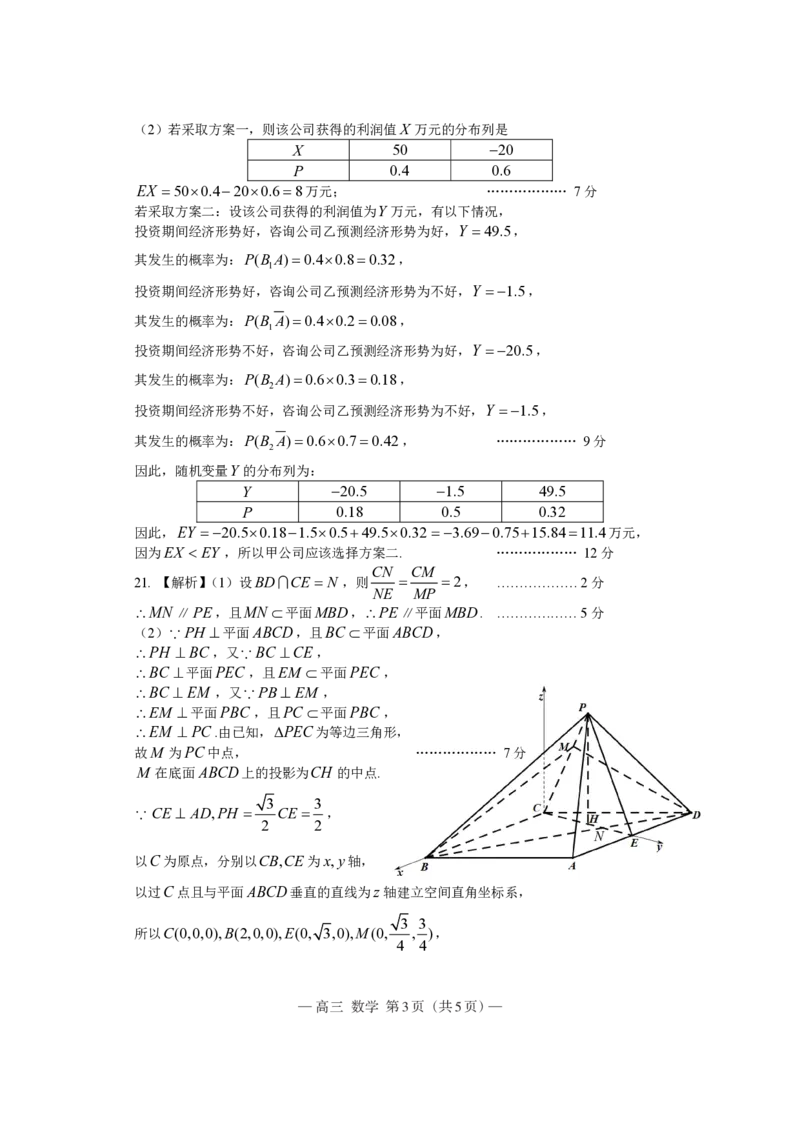……………… 12分 CN CM 21. 【解析】（1）设BD  CE  N ，则  2， ……………… 2分 NE MP MN ∥PE，且MN 平面MBD，PE∥平面MBD. ……………… 5分 （2）  PH 平面ABCD，且BC 平面ABCD， PH BC，又  BC CE， BC 平面PEC ，且EM 平面PEC ， BC  EM ，又  PBEM ， EM 平面PBC ，且PC 平面PBC ， EM PC.由已知，PEC为等边三角形， 故M 为PC中点， ……………… 7分 M 在底面ABCD上的投影为CH 的中点. 3 3  CE  AD,PH  CE  ， 2 2 N 以C为原点，分别以CB,CE为x,y轴， 以过C点且与平面ABCD垂直的直线为z轴建立空间直角坐标系， 3 3 所以C(0,0,0),B(2,0,0),E(0, 3,0),M(0, , )， 4 4 —高三 数学 第 页（共 页）— 3 5  3 3 3 EB(2, 3,0),ME (0, , )， 4 4  设n(x,y,z)是平面EBM 的一个法向量，则   nEB02x 3y0     3 3 3 ， nME 0 y z 0  4 4  令y2，则x 3，z 2 3，即n( 3,2,2 3)， ……………… 9分  BC 平面PEC ，  CB(2,0,0)是平面PEC 的一个法向量， ……………… 10分     nCB 2 3 57 cosn,CB     ， |n||CB| 2 19 19 因为二面角BEM C是一个锐角， 57 所以二面角BEM C的余弦值为 . ……………… 12分 19 c 3 22. 【解析】（1）依题意可知e  ， ……………… 1分 a 2 3 2 由于k 1，则直线MN的方程为xy10，因为点A到直线MN的距离为 . 1 1 2 |a1| 3 2 所以  ，解得a 2， ……………… 3分 2 2 所以c 3，则b a2 c2 1， x2 所以椭圆E的标准方程  y2 1. ……………… 4分 4 1 （2）设M(x ,y ),N(x ,y ),P(x ,y )，直线AB的方程为xmy1.此时k  . 1 1 2 2 1 1 1 m xmy1 联立直线与椭圆方程 消去x得(m2 4)y2 2my30， x2 4y2 4 2m 3 则有y  y  ,y y  ……………… 6分 1 2 m2 4 1 2 m2 4 y y 不妨设Q(x ,y )，因为A ,N,Q三点共线，则k k ，所以则有 0  2 ， 0 0 2 A 2 N A 2 Q x 2 x 2 0 2 y y 因为A,P,Q三点共线，则k k 则有 0  1 ， ……………… 8分 1 A 1 P A 1 Q x 2 x 2 0 1 —高三 数学 第 页（共 页）— 4 5x 2 x 2 my 1 1 x 2 x 2 my 1 1 所以 0  2  2 m ， 0  1  1 m y y y y y y y y 0 2 2 2 0 1 1 1 2m 2x 1 1 m2 4 4m 0 2m(  )2m  ， ……………… 10分 y y y 3 3 0 1 2 m2 4 y 3 3 所以 0  ，所以k  ， ……………… 11分 x 2m 2 2m 0 3 k 3 所以k  k ，所以 2  . ……………… 12分 2 2 1 k 2 1 —高三 数学 第 页（共 页）— 5 5