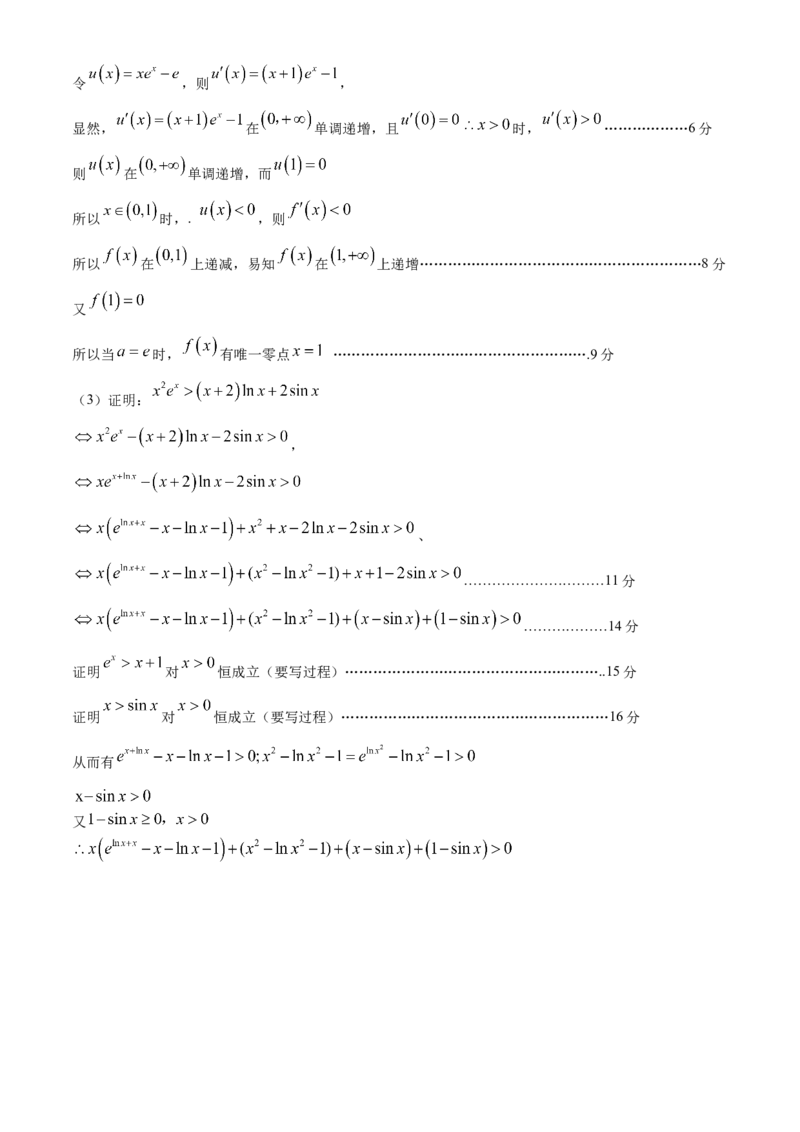文档内容
荆州中学 2021 级高三第三次适应性考试
数学试卷参考答案
1 2 3 4 5 6 7 8 9 10 11
B D A C D D C A ABC ABC AC
8. 设 的中点为 ,设 ,则 ,得
,则 ,设直线 的倾斜角为 ,又 ,所以
,可得 ,所以直线 的倾斜角为 ,则 的斜率为
,所以 ,所以双曲线的渐近线方程为 ,
11. 设点 ,由已知得 ,整理得 ,所以点 的轨迹为曲线 的方程为
,故A正确;又离心率 ,故B不正确;
圆 的圆心 到曲线 的渐近线为 的距离为 ,
又圆 的半径为1,故C正确;
直线 与曲线 的方程联立 整理得 ,设 , ,且 ,
有 ,所以 ,
要满足 ,则需 ,解得 或 或 ,当 ,此时
,而曲线E上 ,所以满足条件的直线有两条,故D不正确,
故选:AC.
14.记事件 “抽取学生是勤生”, 事件 “抽取学生是懒生”, 事件 “抽取学生流下了悔恨的
泪水”,
则依题意有 ,
同理,
故
所以
15.证明:(1) ;
,
……………………………………………………3分
(2)
……………………………6分…………………………………………...7分
……………………………………………………………..8分
(3)
………………………………9分
……………………………….14分(错位相减法操作
程序到位,结果不对可以给到12分,建议只扣2分)
……………………………………………………15分
16. (1)证明 如图,连接BD,设BD∩AC=G,连接EG,FG,EF.
在菱形ABCD中,不妨设GB=1.由∠ABC=120°,可得AG=GC=…………1
分
由BE⊥平面ABCD,AB=BC,可知AE=EC.
又AE⊥EC,
所以 EG=,且 EG⊥AC……………………………………………………………2
分
在Rt △EBG中,可得BE=,故DF=.
在Rt △FDG中,可得FG=.
在直角梯形BDFE中,由BD=2,BE=,DF=,可得EF=,……………4分
从而EG2+FG2=EF2,所以EG⊥FG.又AC∩FG=G,可得EG⊥平面AFC.
因为EG 平面AEC,
所以平面AEC⊥平面AFC……………………………………………………………………7分
⊂
(2)解 如图,以G为坐标原点,分别以GB,GC的方向为x轴,y轴正方向,|GB|为单位长度,建立空间
直角坐标系G-xyz,…………………………………………………………………………8分
由(1)可得A(0,-,0),E(1,0,),F,
C(0,,0)……………………………………………………………………………………9分所以AE=(1,,),CF=.
故cos〈AE,CF〉==-………………………………………………………………14分
所以直线AE与直线CF所成角的余弦值为………………………………………………………15分
17.解:(1)依题意知甲、乙两人所付费用相同时,可能是 元或 元或 元…………………….1分
甲滑雪2小时以上,3小时以内的概率为 ,
乙滑雪2小时以上,3小时以内的概率为 ,………………………………………..2分
所以两人付费均为 元的概率为 ,……………………………………………………..3分
两人付费均为 元的概率为 ………………………………………………………4分
两人付费均为 元的概率为 ……………………………………………..5分
所以,甲、乙两人所付费用的概率为 ………………………..6分
(2) 的所有可能取值为: ,…………………………………………………………7分
则
………………………………………………………………………….8分
…………………………………………………………………………………10分
所以,随机变量 的分布列如下表所示:
0 40 80 120...........................................................................................................................................................................11分
……………………………………………13分
…
…………………………………………………………………………………………………………………….15
分
18.解:(1)设AB的中点为P,切点为Q,连接OP,PQ,取B关于y轴的对称点D,连接AD
则 ,
故
所以点A的轨迹是以B,D为焦点,长轴长为4的椭圆.其中
则曲线C的方程为
………………………………………………………………4分
(2)
……………………………………….6分
……………..8分
解得,
……………………………………………………………………………….9分…………………………………………………………………10分
(3)易得,
…………………………………………….12分
…………………………………………………13分
而
……………………..16分
所以 ,即定值为 ………………………………………..17分
19.解:(1)当 时, ,故 ,…………………1分
所以 ,又 ,…………………………………………………………………..2分
所以,曲线 在点 处的切线方程为 ……………………3分
斜截式方程为 ………………………………………………………………………4分
(2)当 时, ,故 ,令 ,则 ,
显然, 在 单调递增,且 时, ………………6分
则 在 单调递增,而
所以 时,. ,则
所以 在 上递减,易知 在 上递增……………………………………………………8分
又
所以当 时, 有唯一零点 ……………………………………………….9分
(3)证明:
,
、
…………………………11分
………………14分
证明 对 恒成立(要写过程)………………………………………………..15分
证明 对 恒成立(要写过程)…………………………………………………16分
从而有
又