文档内容
2024 年高考数学第一次模拟考试(七省新高考)
数学·全解全析
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.答卷前,考生务必将自己的姓
名、准考证号填写在答题卡上.
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如
需改动,用橡皮擦干净后,再选涂其他答案标号.写在本试卷上无效.
3.回答第Ⅱ卷时,将答案写在答题卡上.写在本试卷上无效.
4.测试范围:高考全部内容
5.考试结束后,将本试卷和答题卡一并交回.
第Ⅰ卷(选择题)
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项
是符合要求的。
1.设i为虚数单位,复数 满足 ,则 ( )
A. B.2 C. D.1
【答案】A
【分析】先求出复数 ,再求 .
【详解】∵ ,∴ .
故选:A
2.已知集合 ,则 ( )
A. B.
C. D.
【答案】B
【分析】直接解一元二次不等式得集合 ,解一元一次不等式的集合 ,从而可得并集 .【详解】因为 ,解得 或 ,所以 或 ,
又 ,所以 或 .
故选:B.
3.“ ”是“方程 表示焦点在x轴上的椭圆”的( )
A.充要条件 B.必要而不充分条件
C.充分而不必要条件 D.既不充分也不必要条件
【答案】A
【分析】由椭圆的标准方程结合充分必要条件的定义即得.
【详解】若 ,则方程 表示焦点在 轴上的椭圆;
反之,若方程 表示焦点在 轴上的椭圆,则 ;
所以“ ”是“方程 表示焦点在x轴上的椭圆”的充要条件.
故选:A.
4.某校高三年级有500人,一次数学考试的成绩X服从正态分布 .估计该校高三年级
本次考试学生数学成绩在120分以上的有( )
参考数据:若 ,则 ,
.
A.75人 B.77人 C.79人 D.81人
【答案】C
【分析】 , ,由概率计算人数即可.
【详解】 , , ,
因为 ,
所以 ,所以数学成绩在 分以上的人数约为 人.
故选:C.
5.唐代诗人李颀的诗《古从军行》开头两句“白日登山望烽火,黄昏饮马傍交河”隐含着一个有
趣的数学问题—“将军饮马”问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再
回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为 ,河岸
线所在直线方程为 ,若将军从点 处出发,并假定将军只要到达军营所在区域即回
到军营,则“将军饮马”的最短路程为( )
A. B. C. D.
【答案】D
【分析】求得 关于直线 的对称点,根据点和圆的位置关系求得正确答案.
【详解】设 关于直线 的对称点为 ,
则 ,解得 ,
圆 的圆心为 ,半径 ,
所以“将军饮马”的最短路程为 .
故选:D
6.已知函数 在区间 上单调递减,则 的取值范围是( )
A. B. C. D.
【答案】D
【分析】复合函数利用“同增异减”求解函数的单调性,求出函数在 上单调递减,从而
得到集合的包含关系,求出 的取值范围.
【详解】令 ,则 .由 在 上单调递减,则 在 上单调递减.
所以 .
所以 ,解得 .故选:D.
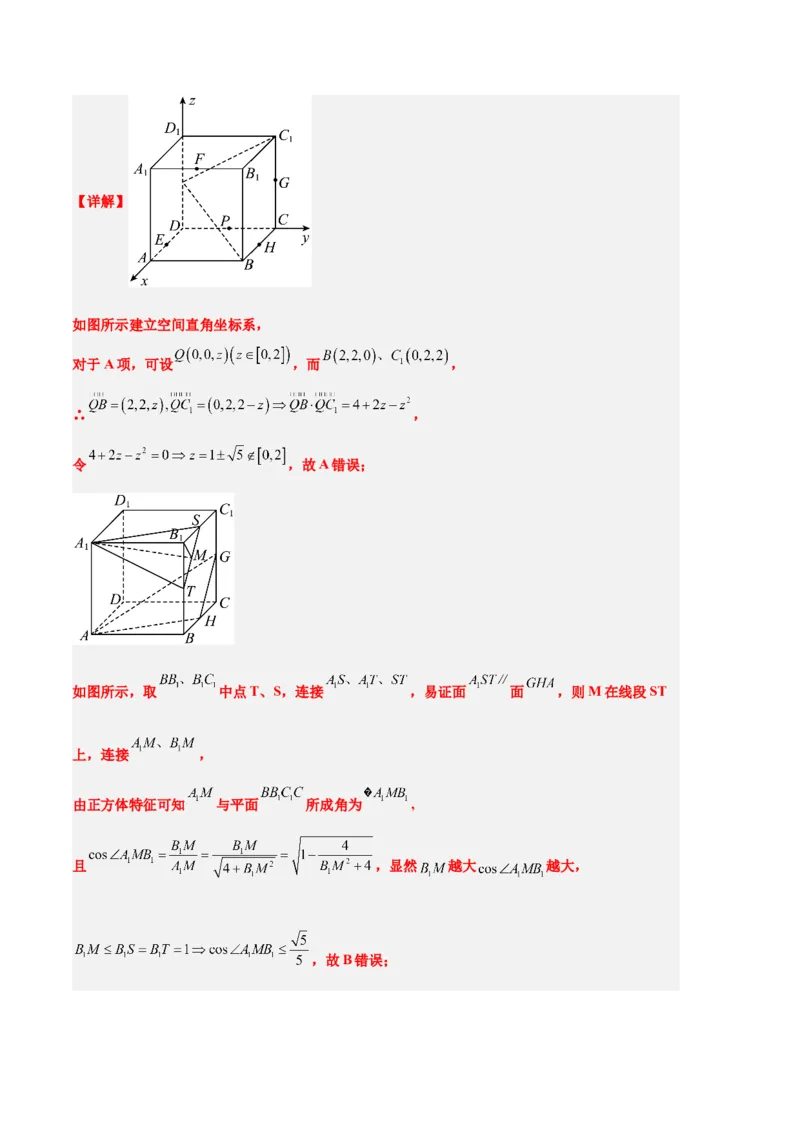
7.如图,在棱长为2的正方体 中, , , , , 均为所在棱的中点,则
下列结论正确的是( )
A.棱 上一定存在点 ,使得
B.设点 在平面 内,且 平面 ,则 与平面 所成角的余弦值的
最大值为
C.过点 , , 作正方体的截面,则截面面积为
D.三棱锥 的外接球的体积为
【答案】C
【分析】对于A,建立空间直角坐标系,由数量积判定即可;对于B,先确定M的位置,由空间
中的线面关系计算即可;对于C,由平面的性质确定截面图象,计算正六边形的面积即可;对于
D,确定球心及球半径计算即可.【详解】
如图所示建立空间直角坐标系,
对于A项,可设 ,而 ,
∴ ,
令 ,故A错误;
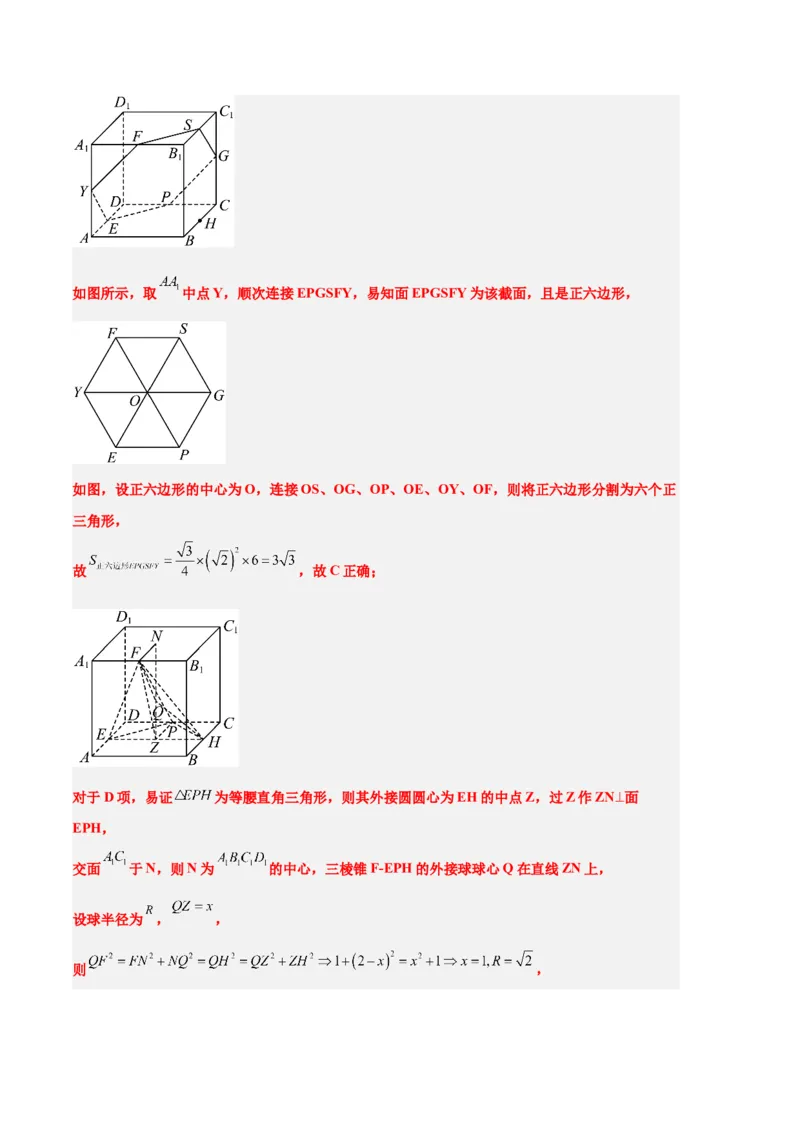
如图所示,取 中点T、S,连接 ,易证面 面 ,则M在线段ST
上,连接 ,
由正方体特征可知 与平面 所成角为 ,
且 ,显然 越大 越大,
,故B错误;如图所示,取 中点Y,顺次连接EPGSFY,易知面EPGSFY为该截面,且是正六边形,
如图,设正六边形的中心为O,连接OS、OG、OP、OE、OY、OF,则将正六边形分割为六个正
三角形,
故 ,故C正确;
对于D项,易证 为等腰直角三角形,则其外接圆圆心为EH的中点Z,过Z作ZN⊥面
EPH,
交面 于N,则N为 的中心,三棱锥F-EPH的外接球球心Q在直线ZN上,
设球半径为 , ,
则 ,故 .
故选:C
8.定义在区间 上的函数 满足: 对 恒成立,其中
为 的导函数,则
A.
B.
C.
D.
【答案】B
【分析】分别构造函数 , , , ,利用导数研究其单调
性即可得出.
【详解】令 , ,
,
, 恒成立,
, ,
, 函数 在 上单调递增,
, .
令 , , ,
, 恒成立,, 函数 在 上单调递减,
, .综上可得: ,
故选:B.
二、多项选择题:本题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符
合题目的要求,全部选对的得5分,部分选对的得2分,有选错的得0分。
9.已知一组样本数据 ,其中 ( ,2,…,15),由这组数据得到另一组新的
样本数据 , ,…, ,其中 ,则( )
A.两组样本数据的样本方差相同
B.两组样本数据的样本平均数相同
C. , ,…, 样本数据的第30百分位数为
D.将两组数据合成一个样本容量为30的新的样本数据,该样本数据的平均数为5
【答案】AC
【分析】根据一组数据加减一个数以及乘以一个数时,平均数以及方差的性质可判断ABD;根据
百分位数的计算可判断C;
【详解】由题意可得: ,
∵ ,则 , ,故A正确,B错误;
由于求 第30百分位数:15×0.3=4.5,故为第5个数,
的排列为: ,
因此,第30百分位数为 ,C正确;
将两组数据合成一个样本容量为30的新的样本数据,
新样本的平均数为 ,D错误,
故选:AC.
10.若函数 ( , , )的图象如图,且 , ,则下列说法正确的是( )
A.函数 的周期为5
B.函数 的对称轴为 ,
C.函数 在 内没有单调性
D.若将 的图象向左平移 ( )个单位长度,得到的函数图象关于 轴对称,则
的最小值为1
【答案】BD
【分析】根据给定的函数及图象,结合“五点法”作图,求出函数 的解析式,再逐项分析、
计算判断作答.
【详解】观察图象知, ,而 ,解得 ,又 ,则 ,
因为 ,由“五点法”作图知, ,解得 ,于是 ,
对于A,函数 的周期 ,A错误;
对于B,由 ,得 ,函数 图象的对称轴为 ,
B正确;
对于C,当 时, ,因此函数 在 上单调递增,C错误;
对于D,将 的图象向左平移 ( )个单位长度,得到函数 的图象,
依题意, ,解得 ,因此 ,D正确.
故选:BD11.已知定义在 上的函数 满足 ,且 为偶函数,则下列说法
一定正确的是( )
A.函数 的周期为2 B.函数 的图象关于 对称
C.函数 为偶函数 D.函数 的图象关于 对称
【答案】BC
【分析】根据给定的信息,推理论证周期性、对称性判断AB;借助变量替换的方法,结合偶函数
的定义及对称性意义判断CD作答.
【详解】依题意, 上的函数 , ,则 ,函数
的周期为4,A错误;
因为函数 是偶函数,则 ,函数 的图象关于 对称,
且 ,即 ,函数 图象关于 对称,B正确;
由 得 ,则函数 为偶函数,C正确;
由 得 ,由 得 ,
因此 ,函数 的图象关于 对称,D错误.
故选:BC
12.已知 是抛物线 的焦点,点 在抛物线 上,过点 的两条互相垂直
的直线 , 分别与抛物线 交于 , 和 , ,过点 分别作 , 的垂线,垂足分别为 ,
,则( )
A.四边形 面积的最大值为2
B.四边形 周长的最大值为C. 为定值
D.四边形 面积的最小值为32
【答案】ABD
【分析】根据给定条件,求出抛物线 的方程,确定四边形 形状,利用勾股定理及均值不
等式计算判断A,B;设出直线 的方程,与抛物线方程联立,求出弦 长即可计算推理判断
C,D作答.
【详解】依题意, ,解得 ,即抛物线 : ,焦点 ,准线方程为:
,直线 , 与坐标轴不垂直,
因为 , ,则四边形 为矩形,有
,
当且仅当 时取等号, ,即四边形 面积的最大值为2,
A正确;
因为 ,则 ,
当且仅当 时取等号,因此四边形 周长 的最大值为 ,B
正确;设直线 方程为: , ,由 消去y得: ,则
,
,同理 ,
因此 ,C错误;
四边形 面积 ,
当且仅当 时取等号,所以四边形 面积的最小值为32,D正确.
故选:ABD
第Ⅱ卷(非选择题)
二、填空题:本大题共4小题,每小题5分,共20分
13.已知向量 是单位向量,且 与 垂直, 与 的夹角为135°,则 .
【答案】
【分析】根据数量积定义与运算律求解.
【详解】由题意 ,∴ ,
故答案为: .
14.已知正四棱台 中, , ,则其体积为 .
【答案】
【分析】作出正四棱台的直观图,过点 作 交 于点 ,过点 作 交 于
点 ,利用勾股定理求出棱台的高,最后根据棱台的体积公式计算可得.
【详解】如图正四棱台 中 ,则 , ,过点 作 交 于点 ,
过点 作 交 于点 ,
则 ,又 ,所以 ,
即正四棱台 的高 ,
所以棱台的体积 .
故答案为:
15.试写出曲线 与曲线 的一条公切线方程 .
【答案】 或 (写出一个即可)
【分析】设出切点坐标,根据切线斜率相等,建立等式,解出即可.
【详解】设公切线 与曲线 切于点 ,
与曲线 切于点 .
由 ,得 .由 ,得 .
令 ,即 ,则 ,
且 ,即 ,
化为 ,
所以 ,解得 或 .
当 时, , ,
此时切线 的方程为 ,即 .
当 时, , ,
此时切线 的方程为 ,即 .
综上可知,切线 的方程为 或 ,写出任意一个即可.
故答案为: 或 ,写出任意一个即可.
16.已知各项都不为0的数列 的前 项和 满足 ,其中 ,设数列 的前
项和为 ,若对一切 ,恒有 成立,则 能取到的最大整数是 .
【答案】
【分析】根据题意推得 ,利用等差数列的通项公式,求得 的通项公式为 ,
得到 ,令 ,结合 ,求得 最小
时为 ,根据 恒成立,求得 ,即可求解.
【详解】因为 ,当 时, ,
两式相减可得 ,即 ,因为数列 的各项都不为0,所以 ,
因为 ,所以 ,
数列 的奇数项是以1为首项,公差为2的等差数列,所以 ;
数列 的偶数项是以2为首项,公差为2的等差数列,所以 ,
故数列 的通项公式为 ,可得 ,所以 ,
令 ,
,
,则 ,
所以 随着 的增大而增大,即 在 处取最小值, ,
又因为对一切 ,恒有 成立,所以 ,解得 ,
故 能取到的最大整数是 .
故答案为: .
三、解答题:本小题共6小题,共70分,其中第17题10分,18~22题12分。解答应写出文字说
明、证明过程或演算步骤.
17.在△ABC中,内角A,B,C所对边分别为a,b,c, .
(1)求cosB;
(2)若b=3,a>c,△ABC的面积为 ,求a.
【答案】(1)
(2)
【分析】(1)由正弦定理得 ,再利用 可得答案;(1)利用 可得 由余弦定理得 ,再由a,c可看作一元二次方程
的两不等实根可得答案.
(1)
因为 ,由正弦定理得
,
因为 ,
所以 ,
所以 ,可得 .
(2)
,∵ ,可得
在△ABC中,由余弦定理得 ,∴ ,
, ,∴a,c可看作一元二次方程 的两不等实根,
∵ ∴ .
18.设同时满足条件:① ;② , 是常数)的无穷数列 叫做 数
列,已知数列 的前 项和 满足 为常数,且 , .
(1)求数列 的通项公式;
(2)设 ,若数列 为等比数列,求 的值;并证明数列 为 数列.
【答案】(1)(2) ,证明见解析
【分析】(1)根据关系 ,结合条件求数列 的通项公式;
(2)根据等比数列性质求 的值;根据 数列的定义证明结论.
【详解】(1)当 时, , .
当 时, ,
整理得 ,又 ,
所以 ,
即数列 是以 为首项、 为公比的等比数列,
;
(2)由(1)知, , ,
所以 , , ,
由数列 是等比数列,则 ,
故 ,解得 ,
再将 代入 式,得 .
因为 ,所以数列 为等比数列,故 满足要求;
由于 ,满足条件①;
又由于 ,故存在 满足条件②.故数列 为 数列.
19.四棱锥 中,四边形 为梯形,其中 , ,
,平面 平面 .
(1)证明: ;
(2)若 ,且 与平面 所成角的正弦值为 ,点 在线段 上且满足 ,
求二面角 的余弦值.
【答案】(1)证明见解析;
(2) .
【分析】(1)由题设可得 ,利用面面垂直的性质可得 面 ,再由线面垂直的性
质证 ;
(2)若 为 中点,连接 ,首先求证 , 两两垂直,构建空间直角坐标系,确定
相关点坐标并令 且 ,根据线面角及向量夹角的坐标表示求参数m,进而可得
,再求面 、面 的法向量,应用向量夹角的坐标运算求二面角余弦值.
(1)
由题设,△ 为等边三角形,则 ,
又四边形 为梯形, ,则 ,
在△ 中, ,即 ,
面 面 ,面 面 , 面 ,则 面 ,
又 面 ,故 .(2)
若 为 中点, ,则 ,
面 面 ,面 面 , 面 ,则 面 ,
连接 ,则 ,且 面 ,故 ,
综上, , 两两垂直,
构建以 为原点, 为x、y、z轴正方向的空间直角坐标系,
所以 , , , ,若 且 ,则 ,
而面 的一个法向量为 , ,
所以 ,可得 ,故 ,
所以 , , ,
若 是面 的一个法向量,则 ,
取 ,若 是面 的一个法向量,则 ,取 ,
所以 ,
由图知:锐二面角 的余弦值 .
20.击鼓传花,也称传彩球,是中国古代传统民间酒宴上的助兴游戏,属于酒令的一种,又称“击
鼓催花”,在唐代时就已出现.杜牧《羊栏浦夜陪宴会》诗句中有“球来香袖依稀暖,酒凸觥心泛
艳光”,可以得知唐代酒宴上击鼓传花助兴的情景.游戏规则为:鼓响时,开始传花(或一小物件),
鼓响时众人开始依次传花,至鼓停为止,此时花在谁手中(或其序位前),谁就上台表演节目(多是唱
歌、跳舞、说笑话:或回答问题、猜谜、按纸条规定行事等).某单位组织团建活动,9人一组,
共9组,玩击鼓传花,组号 (前五组)与组内女性人数 统计结果如表:
x 1 2 3 4 5
y 2 2 3 4 4
若女性人数 与组号 (组号变量 依次为1,2,3,4,5,…)具有线性相关关系.
(1)请求出女性人数 关于组号 的回归直线方程;(参考公式 , )
(2)从前5组中随机抽取3组,若3组中女性人数不低于3人的有 组,求 的分布列与期望.
【答案】(1)
(2)分布列见解析;期望为
【分析】(1)利用已知条件求解回归直线方程的系数, 然后求解回归直线方程(2)由题可知 的
所有可能取值为 ,求出概率得到 的分布列,然后求解期望即可.
(1)
解:由题可得
.,
则
所以
(2)
解:由题可知 的所有可能取值为 , , , ,
, ,
则X的分布列为
∴ .
21.已知双曲线 : 的离心率为 ,直线 : 与双曲线C仅有一
个公共点.
(1)求双曲线 的方程
(2)设双曲线 的左顶点为 ,直线 平行于 ,且交双曲线C于M,N两点,求证: 的垂心
在双曲线C上.
【答案】(1)
(2)证明见解析
【分析】(1)由离心率为 可得 ,再联立直线与双曲线利用判别式可得 的方程;(2)设 方程,及 的坐标,由过A引 的垂线交C于另一点H,可得点H为 .
再证 即可.
【详解】(1)因为双曲线 的离心率为 ,所以 ,即 ,
所以双曲线 的方程为 ,
联立直线 与双曲线 的方程 ,消去 得 ,
即 ,
因为 与双曲线C仅有一个公共点,
所以 ,
解得 ,
故双曲线 的方程为 .
(2)设 , , 则 满足
消去 得 ,
所以 , ,
如图所示,过A引 的垂线交C于另一点H,则AH的方程为 .
代入 得 ,即 (舍去)或 .
所以点H为 .
所以
,
所以 ,
故 为 的垂心,得证.
22.已知函数 , .
(1)讨论函数 的单调性;
(2)证明:当 时, 恒成立.
【答案】(1)答案见解析;
(2)证明见解析.
【分析】(1)对参数 分类讨论,在不同情况下利用导数判断函数单调性,即可求得结果;
(2)将问题转化为证明 ,构造函数 ,利用导数判断其单调
性,结合题意,即可证明.
【详解】(1) 的定义域是 , ,① 时, , 在 单调递增,
② 时, ,
令 ,解得 ;令 ,解得 ,
故 在 递减,在 递增,
综上:
时, 在 单调递增, 时, 在 递减,在 递增.
(2)要证 ,即证 , ,
①当 时, , ,该不等式恒成立;
②当 时, ,结合 ,得 ,
只需证明: ,即证 ,
令 , ,
令 ,则 ,
令 ,则 在 上恒成立,
所以 在 上单调递增,
又 , ,所以存在 ,使得 ,
所以 在 上单调递减,在 上单调递增,又 , , , ,
所以当 时, ;当 时, ,
即函数 在 上单调递减,在 上单调递增,
所以 ,问题得证,
即当 时, 恒成立.
综上所述,当 时, 恒成立.