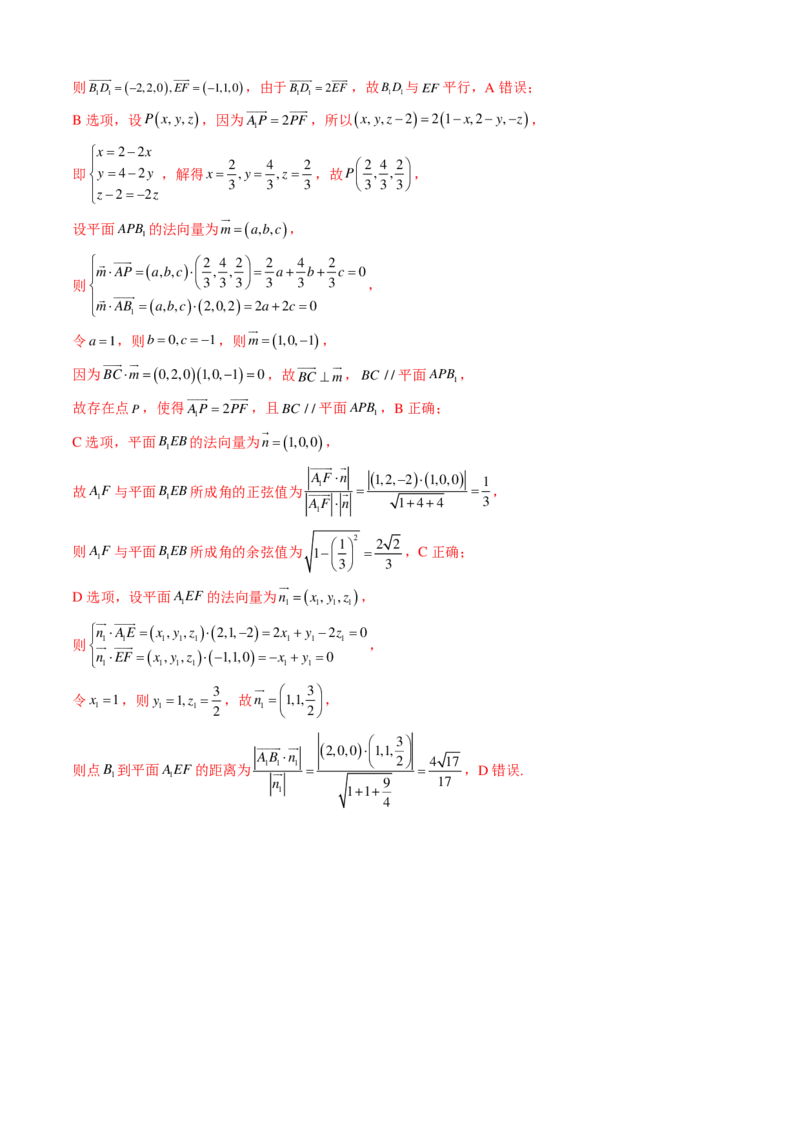文档内容
2024 年高考第二次模拟考试
高三数学
全解全析
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要
求的.
1.设集合A= { x y=ln(x−3)} ,B={ x x≤−1 } ,则A ( B ) =( )
R
A. { x −1< x≤3 } B. { x x>−1 } C. { x x≤−1,或x>3} D. { x x>3 }
【答案】B
【分析】先化简集合,再利用集合的交并补运算求解即可,
【详解】由题意得A={ x x>3 },B={ x x≤−1 } ,又 B={ x x>−1 }
R
则A∪ ( B ) ={ x x>−1 } ,故选:B.
R
z
2.已知复数z=a+bi(a∈R,b∈R且ab),且z2为纯虚数,则 =( )
z
A.1 B.−1 C.i D.−i
【答案】D
【分析】利用复数的概念及四则运算法则运算即可求解.
【详解】因为z=a+bi,所以z2 =(a+bi)2 = ( a2−b2) +2abi,
a2−b2 =0
又因为z2为纯虚数,所以 ,即a=b≠0(舍)或a=−b≠0,
2ab≠0
所以z=a−ai,所以z =a+ai,
z a−ai 1−i (1−i)2
所以 = = = =−i.
z a+ai 1+i (1+i)(1−i)
故选:D
3.已知向量a =(−2,4 ) ,b =( 1,t ),若a 与b 共线,则向量a +b 在向量 j =( 0,1 ) 上的投影向量为( )
A. j B. −j C. 2j D. −2j
【答案】C
【解析】
【分析】根据a
与b
共线,可得−2t−4=0,求得t =−2,再利用向量a
+b
在向量
j
=(
0,1
)
上的投影向
(a+b)⋅ j j
量为 ⋅ ,计算即可得解.
j j
【详解】由向量a =(−2,4 ) ,b =( 1,t ),
若a与b 共线,则−2t−4=0,所以t =−2,
a+b =(−1,2),
所以向量a
+b
在向量 j
=(
0,1
)
上的投影向量为:
(a+b)⋅ j j (−1,2)⋅(0,1)
⋅ = ⋅ j =2j ,
j j 1
故选:C
1
4. “ab>1”是“b> >0”( )
a
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
【答案】B
【解析】
【分析】根据充分条件和必要条件的定义判断.
1
【详解】当a>0时,由ab>1,可得b> >0,
a
1
当a<0时,由ab>1,得b< <0;
a
1
所以“ab>1”不是“b> >0”的充分条件.
a
a>0
1
因为b> >0⇔ ab−1 ,所以ab>1,
a
>0
a
1
所以“ab>1”是“b> >0”的必要不充分条件.
a
故选:B.
【点睛】本题考查不等式性质与充分、必要条件的判定,还考查了理解辨析问题的能力,属于基础题.
5.有甲、乙等五人到三家企业去应聘,若每人至多被一家企业录用,每家企业至少录用其中一人且甲、乙两
人不能被同一家企业录用,则不同的录用情况种数是( )
A.60 B.114 C.278 D.336
【答案】D
【解析】命题意图 本题考查排列与组合的应用.
录用3人,有 C3A3 =60 种情况;录用4 人,有 C4C2A3 −C2A3 =162 种情况;录用 5 人,有
5 3 5 4 3 3 3
C1C2
( 5 4 A3−C2A3)+(C3A3−C1A3)=114种情况.所以共有336种.
A2 3 3 3 5 3 3 3
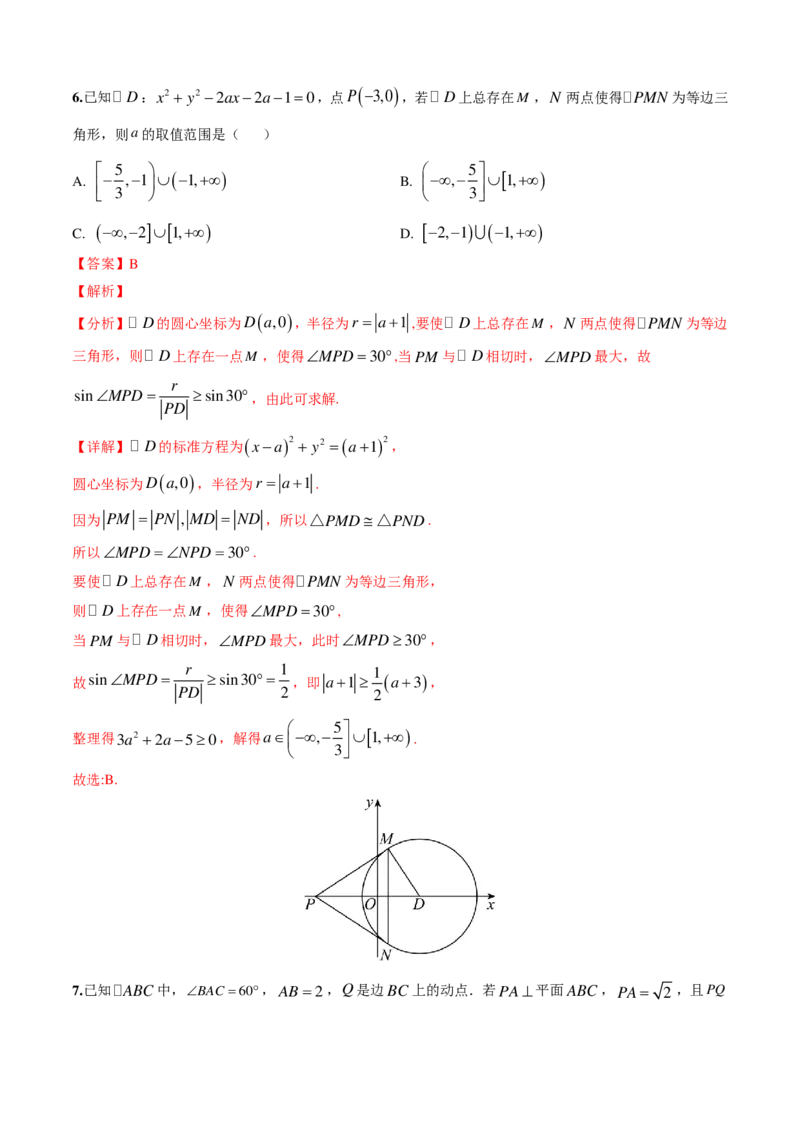
26.已知 D:x2 + y2 −2ax−2a−1=0,点P
(−3,0 )
,若 D上总存在M ,N 两点使得PMN 为等边三
角形,则a的取值范围是( )
5 5
A. − ,−1 ∪(−1,+∞) B. −∞,− ∪[ 1,+∞)
3 3
C.
(−∞,−2 ]∪[ 1,+∞)
D.
[−2,−1 )(−1,+∞)
【答案】B
【解析】
【分析】 D的圆心坐标为D ( a,0 ) ,半径为r = a+1 ,要使 D上总存在M ,N 两点使得PMN 为等边
三角形,则 D上存在一点M ,使得∠MPD=30°,当PM 与 D相切时,∠MPD最大,故
r
sin∠MPD= ≥sin30°,由此可求解.
PD
【详解】 D的标准方程为( x−a )2 + y2 =( a+1 )2,
圆心坐标为D ( a,0 ) ,半径为r = a+1 .
因为 PM = PN , MD = ND ,所以△PMD≅△PND.
所以∠MPD=∠NPD=30°.
要使 D上总存在M ,N 两点使得PMN 为等边三角形,
则 D上存在一点M ,使得∠MPD=30°,
当PM 与 D相切时,∠MPD最大,此时∠MPD≥30°,
r 1 1
故sin∠MPD= ≥sin30°= ,即 a+1 ≥ ( a+3 ),
PD 2 2
5
整理得3a2 +2a−5≥0,解得a∈ −∞,− ∪[ 1,+∞) .
3
故选:B.
7.已知ABC中,∠BAC =60°,AB =2,Q是边BC上的动点.若PA⊥平面ABC,PA= 2 ,且PQ6
与面ABC所成角的正弦值的最大值为 ,则三棱锥P−ABC 的外接球的表面积为( )
3
A. 4π B. 6π C. 8π D. 9π
【答案】B
【解析】
【分析】根据题意得PQ的最小值为 3,AQ的最小值是1,即A到BC的距离为1,则∠ACB=90°,结
合图形找出 ABC的外接圆圆心与三棱锥P−ABC 外接球的球心,求出外接球的半径,再计算它的表面积.
【详解】三棱
△
锥P−ABC 中,PA⊥平面ABC,设直线PQ与平面ABC所成角为θ,
6 PA 2 6
∵sinθ的最大值是 ,∴sinθ= = ≤ ,解得PQ≥ 3,
3 PQ PQ 3
即PQ的最小值为 3,AQ的最小值是1,即A到BC的距离为1,
直角三角形 ABQ中,AB=2,所以∠BAQ=60°,又∠BAC=60°,
所以A,Q重△合,则∠ACB=90°,
则 ABC的外接圆圆心M为AB的中点,
△
又PA⊥平面ABC,从而外接球的球心O为PB的中点,
AB 2 PA 2 2 2 6
外接球的半径R=OB= MB2 +MO2 = + = 12 + = ,
2 2 2 2
2
6
∴三棱锥P−ABC 的外接球的表面积S =4πR2 =4π× =6π.
2
故选:B.
8.加斯帕尔-蒙日是1819世纪法国著名的几何学家.如图,他在研究圆锥曲线时发现:椭圆的任意两条互相
垂直的切线的交点都在同一个圆上,其圆心是椭圆的中心,这个圆被称为“蒙日圆”.若长方形G的四边均
x2 y2
与椭圆M : + =1相切,则下列说法错误的是( )
6 43
A.椭圆M 的离心率为 B.椭圆M 的蒙日圆方程为x2+y2 =10
3
C.若G为正方形,则G的边长为2 5 D.长方形G的面积的最大值为18
【答案】D
【分析】由椭圆标准方程求得a,b后再求得c,从而可得离心率,利用特殊的长方形(即边长与椭圆的轴平
行)求得蒙日圆方程,从而可得长方形边长的关系,结合基本不等式得面积最大值,并得出长方形为正方
形时的边长.
2 3
【详解】由椭圆方程知a= 6,b=2,则c= 6−4 = 2,离心率为e= = ,A正确;
6 3
当长方形G的边与椭圆的轴平行时,长方形的边长分别为2 6和4,其对角线长为 24+16 =2 10,因此蒙
日圆半径为 10,圆方程为x2+y2 =10,B正确;
设矩形的边长分别为m,n,因此m2+n2 =40≥2mn,即mn≤20,当且仅当m=n时取等号,所以长方形G的
面积的最大值是20,此时该长方形G为正方形,边长为2 5,C正确,D错误.
故选:D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部
选对的得6分,部分选对的得部分分,有选错的得0分.
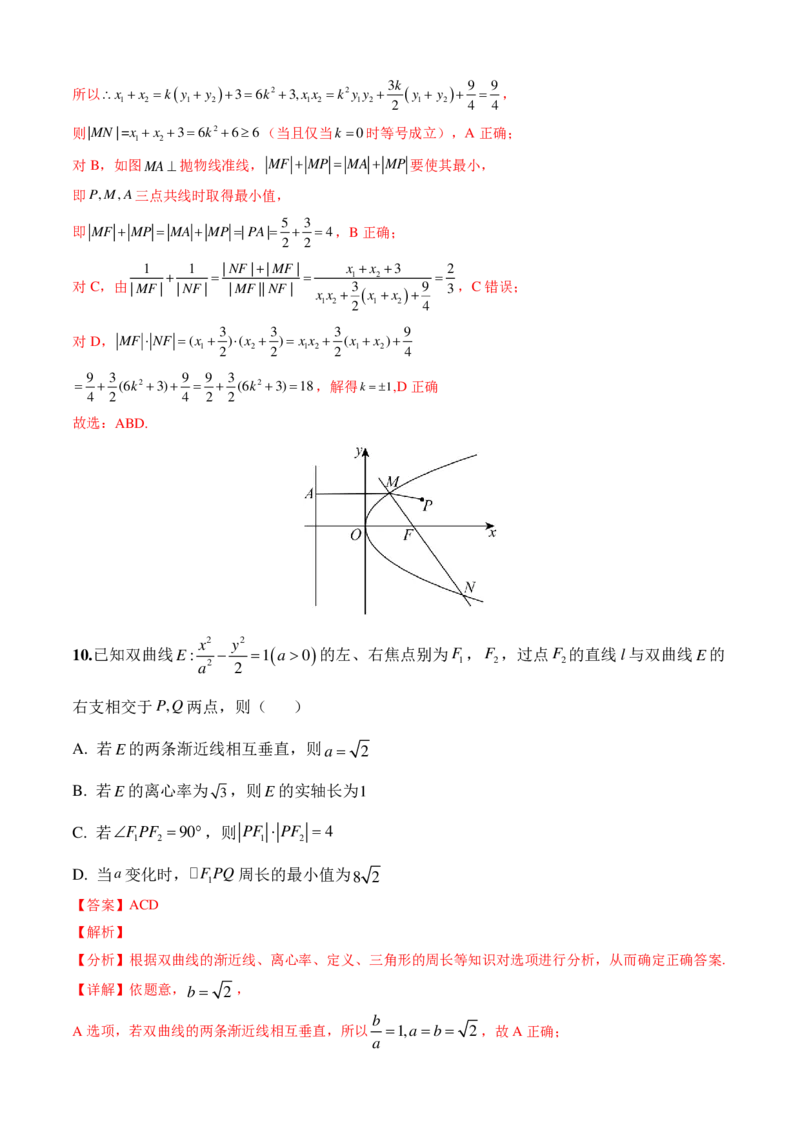
9.已知抛物线C: y2 =6x的焦点为F,过点F的直线交C于M,N两个不同点,则下列结论正确的
是( )
5
A. MN 的最小值是6 B.若点P ,2 ,则 MF + MP 的最小值是4
2
1 1
C. + =3 D.若 MF ⋅ NF =18,则直线MN的斜率为±1
MF NF
【答案】ABD
【分析】A,根据|MN|=x +x + p结合基本不等式即可判断;B,由抛物线定义知当P,M,A三点共线时
1 2
MF + MP ;C,D,设直线方程,联立抛物线,应用韦达定理即可求解.
【详解】对A,设M(x,y ),N(x ,y ),(x,x >0),
1 1 2 2 1 2
因为这些MN倾斜角不为0,
3
则设直线MN的方程为x=ky+ ,联立抛物线得y2−6ky−9=0,
2
则y +y =6k,y ⋅y =−9,
1 2 1 23k 9 9
所以∴x +x =k(y +y )+3=6k2+3,xx =k2y y + (y +y )+ = ,
1 2 1 2 1 2 1 2 2 1 2 4 4
则|MN|=x +x +3=6k2+6≥6(当且仅当k =0时等号成立),A正确;
1 2
对B,如图MA⊥抛物线准线, MF + MP = MA + MP 要使其最小,
即P,M,A三点共线时取得最小值,
5 3
即 MF + MP = MA + MP =|PA|= + =4,B正确;
2 2
1 1 |NF|+|MF| x +x +3 2
+ = = 1 2 =
对C,由|MF| |NF| |MF||NF| xx + 3 (x +x )+ 9 3,C错误;
1 2 2 1 2 4
3 3 3 9
对D, MF ⋅ NF =(x + )⋅(x + )=xx + (x +x )+
1 2 2 2 1 2 2 1 2 4
9 3 9 9 3
= + (6k2+3)+ = + (6k2+3)=18,解得k=±1,D正确
4 2 4 2 2
故选:ABD.
x2 y2
10.已知双曲线E: − =1 ( a >0 )的左、右焦点别为F ,F ,过点F 的直线l与双曲线E的
a2 2 1 2 2
右支相交于P,Q两点,则( )
A. 若E的两条渐近线相互垂直,则 a = 2
B. 若E的离心率为 3 ,则E的实轴长为1
C. 若∠FPF =90°,则 PF ⋅ PF =4
1 2 1 2
D. 当a变化时,FPQ周长的最小值为 8 2
1
【答案】ACD
【解析】
【分析】根据双曲线的渐近线、离心率、定义、三角形的周长等知识对选项进行分析,从而确定正确答案.
【详解】依题意,b= 2 ,
b
A选项,若双曲线的两条渐近线相互垂直,所以 =1,a =b= 2,故A正确;
ac c2 a2 +b2 b 2 2 2
B选项,若E的离心率为e= a = a2 = a2 = 1+ a = 1+ a = 3,
解得a =1,所以实轴长2a=2,故B错误;
PF − PF =2a
C选项,若∠FPF =90°,则 1 2 ,
1 2 PF 2 + PF 2 =4c2
1 2
整理得2 PF ⋅ PF =4c2 −4a2 =4b2 =8, PF ⋅ PF =4,故C正确;
1 2 1 2
PF − PF =2a
D选项,根据双曲线的定义可知, 1 2 ,
QF − QF =2a
1 2
两式相加得 PF + QF − PQ =4a, PF + QF =4a+ PQ ,
1 1 1 1
所以FPQ周长为4a+2 PQ ,
1
2b2 4
当PQ⊥ FF 时, PQ 取得最小值 = ,
1 2
a a
8 8
所以4a+2 PQ ≥4a+ ≥2 4a⋅ =8 2 ,
a a
8
当且仅当4a= ,即a = 2时,等号成立,
a
所以FPQ周长的最小值为8 2,故D正确.
1
故选:ACD
11.在棱长为2的正方体ABCD−ABCD 中,E,F分别是棱BC,CD的中点,则( )
1 1 1 1
A.BD与EF是异面直线
1 1
B.存在点
P
,使得AP=2PF,且BC //平面APB
1 1
2 2
C.AF与平面BEB所成角的余弦值为
1 1
3
4
D.点B 到平面AEF的距离为
1 1 5
【答案】BC
2 4 2
【分析】A选项,建立空间直角坐标系,根据BD =2EF得到BD与EF平行;B选项,先求出P , , ,
1 1 1 1 3 3 3
得到平面APB 的法向量m=(1,0,−1),根据数量积为0得到BC⊥m,得到BC //平面APB ;C选项,先求
1 1
出AF与平面BEB所成角的正弦值,进而求出余弦值;D选项,求出平面AEF的法向量,根据点到平面距
1 1 1
离公式求出答案.
【详解】A选项,以A作坐标原点,AB,AD,AA所在直线分别为x,y,z轴,建立空间直角坐标系,
1
B (2,0,2),D (0,2,2),E(2,1,0),F(1,2,0),A (0,0,2),B(2,0,0),C(2,2,0),
1 1 1
则BD =(−2,2,0),EF =(−1,1,0),由于BD =2EF,故BD与EF平行,A错误;
1 1 1 1 1 1
B选项,设P(x,y,z),因为AP=2PF,所以(x,y,z−2)=2(1−x,2−y,−z),
1
x=2−2x
2 4 2 2 4 2
即y=4−2y ,解得x= ,y= ,z= ,故P , , ,
3 3 3 3 3 3
z−2=−2z
设平面APB 的法向量为m=(a,b,c),
1
2 4 2 2 4 2
m⋅AP=(a,b,c)⋅ , , = a+ b+ c=0
则 3 3 3 3 3 3 ,
m ⋅ A B
1
=(a,b,c)⋅(2,0,2)=2a+2c=0
令a=1,则b=0,c=−1,则m=(1,0,−1),
因为BC⋅m=(0,2,0)(1,0,−1)=0,故BC⊥m,BC //平面APB ,
1
故存在点P,使得AP=2PF,且BC //平面APB ,B正确;
1 1
C选项,平面BEB的法向量为n=(1,0,0),
1
A
1
F⋅n (1,2,−2)⋅(1,0,0)
1
故AF与平面BEB所成角的正弦值为 = = ,
1 1 AF ⋅ n 1+4+4 3
1
2
1 2 2
则A 1 F与平面B 1 EB所成角的余弦值为 1− = ,C正确;
3 3
D选项,设平面AEF的法向量为n =(x,y ,z ),
1 1 1 1 1
n ⋅AE=(x,y ,z )⋅(2,1,−2)=2x +y −2z =0
则1 1 1 1 1 1 1 1 ,
n
1
⋅EF =(x
1
,y
1
,z
1
)⋅(−1,1,0)=−x
1
+y
1
=0
3 3
令x =1,则y =1,z = ,故n =1,1, ,
1 1 1 2 1 2
则点B 到平面AEF的距离为 A 1 B 1 ⋅n 1 = (2,0,0)⋅ 1,1, 3 2 = 4 17 ,D错误.
1 1
n 9 17
1 1+1+
4故选:BC
三、填空题:本题共3小题,每小题5分,共15分.
n
2
12.若二项式 x+
的展开式中二项式系数之和为64,则二项展开式中系数最大的项为
x
【答案】240
【解析】
n
2
【详解】因为二项式 x+
的展开式中二项式系数之和为64,
x
6
2
所以2n =64,得n=6,所以二项式为 x+
,
x
2 6− 3 r
则二项式展开式的通项T =Crx6−r( )r =Cr2rx 2 ,
r+1 6 6
x
Cr2r ≥Cr−12r−1
11 14
令第r+1项的系数最大,则 6 6 ,解得 ≤r ≤ ,
Cr2r ≥Cr+12r+1 3 3
6 6
3
因为r∈N,所以r =4,则二项展开式中系数最大的项为 T =C424x 6− 2 ×4 =240 ,所以填240
5 6
13.若函数 f
(
x
)=ax+sinx
的图像上存在两条互相垂直的切线,则实数a 是__________.
【答案】0
【解析】
【详解】注意到,
f′(
x
)=a+cosx.
若函数 f ( x ) 上存在两条切线垂直,则存在x 、x ∈R,使得
1 2
f′( x ) f′( x )=−1⇔( a+cosx )( a+cosx )=−1
1 2 1 2
⇔ a2 +a ( cosx +cosx )+cosx ⋅cosx +1=0
1 2 1 2 cosx +cosx 2 cosx −cosx 2
⇔ a+ 1 2
+1−
1 2
=0
2 2
⇔cosx =−cosx =±1,a=0.
1 2
故答案为0
1 1
14. 若过点 ( 0,1 ) 的直线l自左往右交抛物线y = x2及圆x2 +( y−1 )2 = 于A,B,C,D四点,则
4 4
AB +3CD 的最小值为________.
【答案】2 3+2
【解析】
1 1
【分析】根据抛物线的定义求得求出 AB = y + , CD = y + ,当l ⊥ y轴时,则y = y =1,可求
A 2 D 2 D A
AB +3CD 的值;当直线方程为x=n ( y−1 ) 时,代入抛物线方程,根据韦达定理结合基本不等式求得此
时 AB +3CD 的最小值,即可得结论.
1
【详解】解:如图,其中抛物线y = x2的焦点坐标为F ( 0,1 ) ,
4
1 1
抛物线的准线方程为:y =−1,圆x2 +( y−1 )2 = 的半径r =
4 2
又抛物线的定义可得: AF = y +1, DF = y +1,又
A D
1 1
AB = AF − BF = y + , CD = DF − CF = y + ,
A 2 D 2
1 1
当l ⊥ y轴时,则y = y =1,所以 AB +3CD =1+ +31+ =6;
A D 2 2
当l不垂直于y轴时,设l的方程为:x=n ( y−1 ) ,代入抛物线方程得:n2y2 − ( 2n2 +4 ) y+n2 =0,
2n2 +4
所以y + y = ,y ⋅y =1。
A D n2 A D
所以 AB +3CD =2+ y +3y ≥2+2 3y ⋅y =2+2 3,
A D A D
3
当且仅当y =3y ,即y = ,y = 3时,等号成立.
A D D 3 A综上, AB +3CD 的最小值为2+2 3.
故答案为:2+2 3.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)已知数列 { a } 的前n项和为S ,且对于任意的n∈N*都有3S =2a +1.
n n n n
{ }
(1)求数列 a 的通项公式;
n
(2)记数列 { a } 的前n项中的最大值为M ,最小值为m ,令b = M n +m n ,求数列 { b } 的前20项和T .
n n n n 2 n 20
【答案】(1)a =(−2 )n−1
n
5−219
(2)T =
20 6
【解析】
【分析】(1)根据3S =2a +1可得 { a } 是以公比为−2的等比数列,进而可求解,
n n n
(2)根据数列 { a } 的通项性质可对n分奇偶,进而可得M ,m ,分组求和即可求解.
n n n
【小问1详解】
对于任意的n∈N*都有3S =2a +1,
n n
当n≥2时,3S =2a +1,两式相减得3 ( S −S )=( 2a +1 )−( 2a +1 ),即
n−1 n−1 n n−1 n n−1
3a =2a −2a ( n≥2 ) ,
n n n−1
进而得a =−2a ( n≥2 ) , ...................................................4分
n n−1
当n=1时,3S =2a +1,故a =1,
1 1 1
{ }
所以数列 a 是以首项为1,公比为−2的等比数列,
n
所以a =(−2 )n−1 .............................................6分
n
【小问2详解】
当n为奇数时,a =2n−1,且a >0,当n为偶数时,a =−2n−1,且a <0,
n n n n
因此当n为大于1的奇数时, { a } 的前n项中的最大值为a =(−2 )n−1,最小值为a =(−2 )n−2,此时
n n n−1
M +m a +a
b = n n = n n−1 ,
n 2 2
因此当n为偶数时, { a } 的前n项中的最大值为a =(−2 )n−2,
n n−1
最小值为a =(−2 )n−1,此时b = M n +m n = a n−1 +a n , .............................................10分
n n 2 2
当n=1时,b =a ,
1 1{ }
因此 b 的前20项和
n
a +a a +a a +a
T =b +( b +b ++b )+( b +b +b ++b )=a + 3 2 + 5 4 ++ 19 18
20 1 3 5 19 2 4 6 20 1 2 2 2
a +a a +a a +a a S +S 1 S +S +a 1 (−2 )19
+ 1 2 + 3 4 ++ 19 20 = 1 + 19 20 = + 19 19 20 =S + +
2 2 2 2 2 2 2 19 2 2
1−(−2 )19 1 (−2 )19 5−219
= + + = .............................................13分
1+2 2 2 6
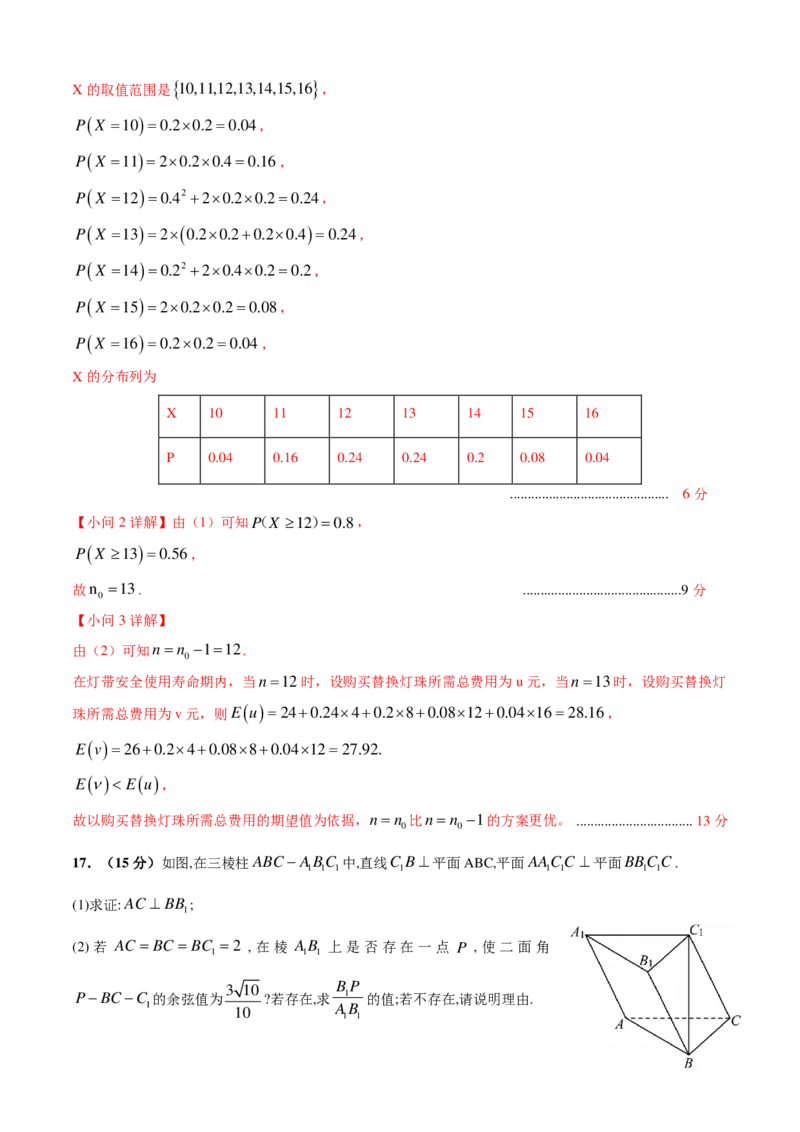
16.(15分)灯带是生活中常见的一种装饰材料,已知某款灯带的安全使用寿命为5年,灯带上照明的灯
珠为易损配件,该灯珠的零售价为4元/只,但在购买灯带时可以以零售价五折的价格购买备用灯珠,该灯
带销售老板为了给某顾客节省装饰及后期维护的支出,提供了150条这款灯带在安全使用寿命内更换的灯
珠数量的数据,数据如图所示.以这150条灯带在安全使用寿命内更换的灯珠数量的频率代替1条灯带更换
的灯珠数量发生的概率,若该顾客买1盒此款灯带,每盒有2条灯带,记X表示这1盒灯带在安全使用寿命
内更换的灯珠数量,n表示该顾客购买1盒灯带的同时购买的备用灯珠数量.
(1)求X 的分布列;
(2)若满足P(X ≥n)≤0.6的n的最小值为n ,求n ;
0 0
(3)在灯带安全使用寿命期内,以购买替换灯珠所需总费用的期望值为依据,比较n=n −1与n=n 哪种
0 0
方案更优.
【答案】(1)分布列见解析;
(2)13; (3)n=n 更优
0
【解析】
【分析】(1)由条件确定随机变量X 的可能取值,再求其取各值的概率,由此可得分布列;
(2)根据分布列结合条件求n的最小值;
(3)分别计算n=n −1与n=n 时购买替换灯珠所需总费用的期望值,比较大小确定结论.
0 0
【小问1详解】
设ξ表示1条灯带在安全使用寿命内更换的灯珠数量,
则P ( ξ =5 )=P ( ξ =7 )=P ( ξ =8 )=0.2,P ( ξ =6 )=0.4,{ }
X的取值范围是 10,11,12,13,14,15,16 ,
P ( X =10 )=0.2×0.2=0.04,
P ( X =11 )=2×0.2×0.4=0.16,
P ( X =12 )=0.42 +2×0.2×0.2=0.24,
P ( X =13 )=2×( 0.2×0.2+0.2×0.4 )=0.24,
P ( X =14 )=0.22 +2×0.4×0.2=0.2,
P ( X =15 )=2×0.2×0.2=0.08,
P ( X =16 )=0.2×0.2=0.04,
X的分布列为
X 10 11 12 13 14 15 16
P 0.04 0.16 0.24 0.24 0.2 0.08 0.04
............................................. 6分
【小问2详解】由(1)可知P(X ≥12)=0.8,
P ( X ≥13 )=0.56,
故n =13. .............................................9分
0
【小问3详解】
由(2)可知n=n −1=12.
0
在灯带安全使用寿命期内,当n=12时,设购买替换灯珠所需总费用为u元,当n =13时,设购买替换灯
珠所需总费用为v元,则E
(
u
)=24+0.24×4+0.2×8+0.08×12+0.04×16=28.16,
E
(
v
)=26+0.2×4+0.08×8+0.04×12=27.92.
E
(ν)<
E
(
u
)
,
故以购买替换灯珠所需总费用的期望值为依据,n=n 比n=n −1的方案更优。 ................................. 13分
0 0
17.(15分)如图,在三棱柱ABC−ABC 中,直线C B⊥平面ABC,平面AACC ⊥平面BBCC.
1 1 1 1 1 1 1 1
(1)求证:AC ⊥ BB ;
1
(2)若 AC = BC = BC =2 ,在棱 AB 上是否存在一点 P ,使二面角
1 1 1
BP
3 10
P−BC−C 的余弦值为 ?若存在,求 1 的值;若不存在,请说明理由.
1 10 AB
1 117.【解析】(1)在平面BBCC中作BH ⊥CC 于H ,
1 1 1
因为平面AACC ⊥平面BBCC,
1 1 1 1
且平面AACC∩平面BBCC =CC ,
1 1 1 1 1
所以BH ⊥平面AACC,从而
1 1
AC ⊥ BH . .............................................4分
在三棱柱ABC−ABC 中,C B⊥平面ABC,AC ⊂平面ABC,
1 1 1 1
所以AC ⊥C B.
1
又因为BC ∩BH = B,所以AC ⊥平面BBCC,因此
1 1 1
AC ⊥ BB . .............................................7分
1
(2)由(1)可知,CA,CB,BC 两两垂直,如图,以C为原点建立空间直角坐标系.
1
则A(2,0,0),B(0,2,0),C (0,2,2),B (0,4,2),B A = BA=(2,−2,0).
1 1 1 1
设BP=λB A =(2λ,−2λ,0),λ∈[0,1],
1 1 1
则P(2λ,4−2λ,2). .............................................9分
设平面PBC的一个法向量为n =(x,y,z),
1
因为BP=(2λ,2−2λ,2),CB=(0,2,0),
n ⋅BP=0, 2λx+(2−2λ)y+2z =0,
所以 1 即
n ⋅CB=0, 2y =0,
1
z =−λx,
则有
y =0.
令x=1,得n =(1,0,−λ).10分
1
而平面BCC 的一个法向量可以是n =(1,0,0),
1 2
n ⋅n (1,0,−λ)⋅(1,0,0) 3 10 1
则 cos n ,n = 1 2 = = ,解得λ= ,
1 2 n ⋅ n 1+λ2 10 3
1 2
BP 1
即P为棱B A 的三等分点, 1 = . .............................................15分
1 1 AB 3
1 1
18.(17分)已知函数 f(x)=lnx−x+a.
(1)若直线y=(e−1)x与函数 f(x)的图象相切,求实数a的值;x
(2)若函数g(x)=xf(x)有两个极值点x和x,且x 1+ln( 1).(e为自然对数的底数).
1 2 1 2 2 1 x
2
【答案】(1)2;(2)证明见解析.
【分析】(1)求出函数 f(x)的导数,利用导数的几何意义结合已知求出a的值.
(2)求出函数g(x)及其导数,确定g(x)有两个极值点的条件,再由g′(x )=0,g′(x )=0变形并构造函数,
1 2
利用导数推理论证即得.
1
【详解】(1)依题意,设切点(x ,lnx −x +a),求导得 f′(x)= −1,
0 0 0 x
1 1
则 f′(x )= −1=e−1,解得x = ,又 f(x )=(e−1)x ,(e−1)x =lnx −x +a,则a=2,
0 x 0 e 0 0 0 0 0
0
所以实数a的值为2. ............................................. 6分
(2)依题意,g(x)=x(lnx−x+a)的定义域为(0,+∞),
1
求导得g′(x)=lnx−x+a+( −1)x=lnx−2x+a+1,
x
则g′(x)=0有两个不等的正根x,x ,且是g′(x)的变号零点,
1 2
1
令h(x)=lnx−2x+a+1,x>0,求导得h′(x)= −2,
x
1 1
当00,当x> 时,h′(x)<0,
2 2
1 1
于是函数h(x)在(0, )上单调递增,在( ,+∞)上单调递减,
2 2
1
由函数h(x)有两个零点,得h(x) =h( )=a−ln2>0,解得a>ln2, .............................................9分
max 2
1
此时h(e−3a)=−2a−2e−3a +1<1−2ln2<0,令ϕ(a)=lna−a+1,求导得ϕ′(a)= −1,
a
当ln20,
当a>1时,ϕ′(a)<0,函数ϕ(a)在(ln2,1)上递增,在(1,+∞)上递减,
则ϕ(a)≤ϕ(1)=0,即lna−a+1≤0,h(2a)=ln2a−3a+1=(lna−a+1)+(ln2−a)−a<0,
1
因此当a>ln2时,函数h(x)必有两个零点x,x ,且是变号零点,由x 1+ln( 1),只需证 >1+lnt,
2 1 x 2(t−1)
2
3lnt−tlnt 2(t−1)
即 >1,只证lnt− <0,
2(t−1) 3−t
2(t−1)
令F(t)=lnt− ,00,
t (3−t)2 t(3−t)2 t(3−t)2
因此函数F(t)在(0,1)上单调递增,F(t)1+ln( 1). .............................................17分
2 1 x
2
【点睛】思路点睛:涉及函数的双零点问题,不管待证的是两个变量的不等式,还是导函数的值的不等式,
都是把双变量的等式或不等式转化为一元变量问题求解,途径都是构造一元函数.
19.(17分)阿波罗尼斯是古希腊著名数学家,他的主要研究成果集中在他的代表作《圆锥曲线》一书中.
阿 波 罗 尼 斯 圆 是 他 的 研 究 成 果 之 一 , 指 的 是 已 知 动 点 M 与 两 定 点 Q,P 的 距 离 之 比
|MQ|
=λ(λ>0,λ≠1 ) ,λ是一个常数,那么动点M的轨迹就是阿波罗尼斯圆,圆心在直线PQ上.已知动
|MP|
x2 y2
点 M 的轨迹是阿波罗尼斯圆,其方程为x2 + y2 =4,定点分别为椭圆C: + =1(a>b>0)的右焦点
a2 b2
1
F 与右顶点A,且椭圆C的离心率为e= .
2
(1)求椭圆C的标准方程;
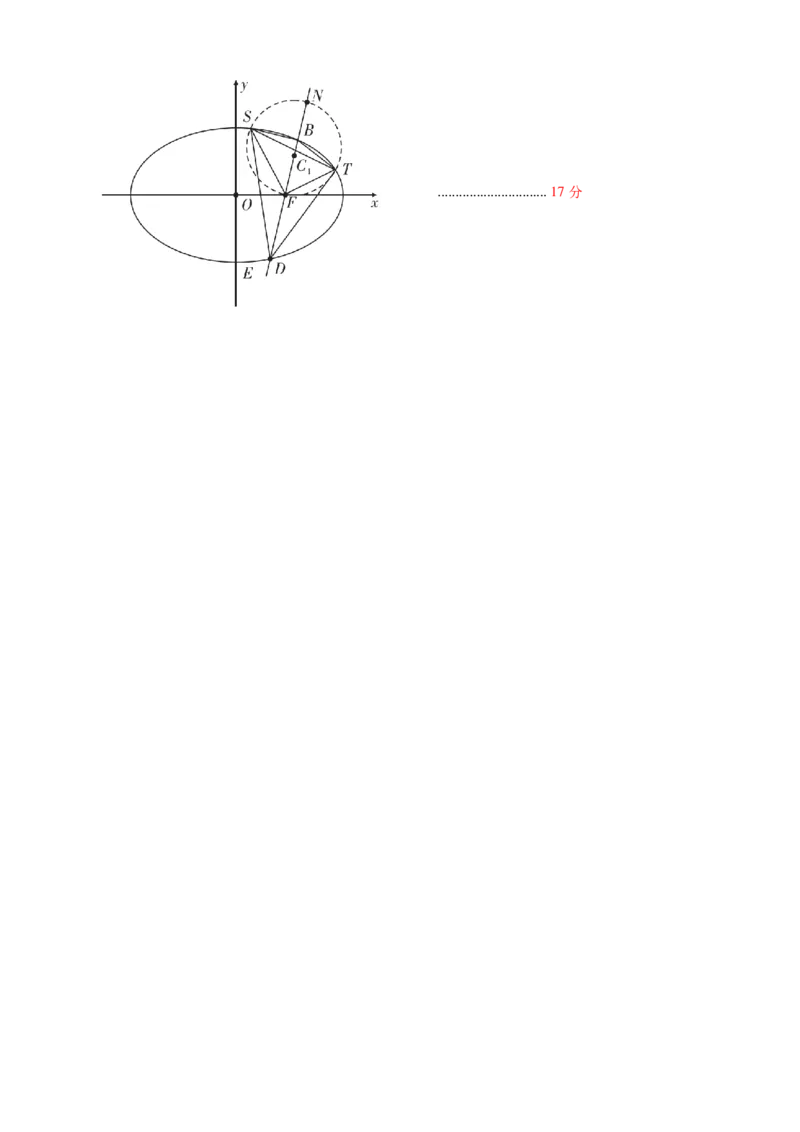
(2)如图,过右焦点F斜率为k(k >0)的直线l与椭圆C相交于B,D(点B在x轴上方),点S,T是椭圆C上异
于B,D的两点,SF平分∠BSD,TF 平分∠BTD.
|BF |
(1)求 的取值范围;
|DF |
(2)将点 S、F、T 看作一个阿波罗尼斯圆上的三点,若 SFT 外接圆的面
81π
积为 ,求直线l的方程. △
8
x2 y2 1 5 10
19.【答案】(1) + =1(2)(1) ,1(2)y = x−
8 6 3 2 2
|c−2| c+2
【解析】(1)方法(1)特殊值法,令M(±2,0), = ,且a=2c,解得c2 =2.
|a−2| a+2
x2 y2
∴a2 =8,b2 =a2 −c2 =6,椭圆C的方程为 + =1, ............................................. 5分
8 6
|MF | (x−c)2 + y2
方法(2)设M(x,y),由题意 = =λ(常数),整理得:
|MA| (x−a)2 + y22c−2aλ2
=0
2c−2aλ2 λ2a2 −c2 λ2 −1 c 1
x2 + y2 + x+ =0,故 ,又 = ,解得:a =2 2,c= 2.
λ2 −1 λ2 −1 λ2a2 −c2 a 2
=−4
λ2 −1
x2 y2
∴b2 =a2 −c2 =6,椭圆C的方程为 + =1. ............................................. 5分
8 6
1
|SB|⋅|SF |⋅sin∠BSF
S |SB| S |BF |
(2)(1) SBF = 2 = ,又 SBF = ,
S 1 |SD| S |DF |
SDF |SD|⋅|SF |⋅sin∠DSF SDF
2
|BS| |BF | |BF |
∴ = (或由角平分线定理得),令 =λ ,则BF =λFD,设D ( x ,y ) ,
|DS| |DF | |DF | 0 0
x = 2(λ+1)−λx
则有3x2 +4y2 =24,又直线l的斜率k >0,则x ∈(−2 2, 2), B 0
0 0 0 y =−λy
B 0
2 ( )
代人3x2 +4y2 −24=0得:3 2(1+λ)−λx +4λ2y2 −24=0,即(λ+1) 5λ−3− 2λx =0,
0 0 0
3 1
λ>0,∴λ= ∈ ,1. ............................... 11分
5− 2x 3
0
|SB| |TB| |BF |
(2)由(1)知, = = ,由阿波罗尼斯圆定义知,
|SD| |TD| |DF |
S,T,F在以B,D为定点的阿波罗尼斯圆上,设该圆圆心为C ,半径为r,与直线l的另一个交点为N ,则有
1
1
|BF | |NB| |BF | 2r−|BF | r =
= ,即 = ,解得: 1 1 .
|DF | |ND| |DF | 2r+|DF | −
|BF | |DF |
81 9 1 1 2 2
又S =πr2 = π,故r = ,∴ − = 13分
Ô² C 1 8 2 2 |BF | |DF | 9
( )2 ( )2 3 1
又|DF |= x − 2 + y2 = x − 2 +6− x2 =2 2− x ,
0 0 0 4 0 2 0
1 1 1 1 5− 2x 1 2− 2x 2 2
∴ − = − = 0 − = 0 =
|BF | |DF | λ|DF | |DF | 1 1 1 9 ,
32 2− x 2 2− x 32 2− x
2 0 2 0 2 0
2 3 3 10 −y 5 5 10
解得:x =− ,y =− 6− x2 =− ,∴k = 0 = ,∴直线l的方程为y = x− .
0 2 0 4 0 4 2−x 2 2 2
0............................... 17分