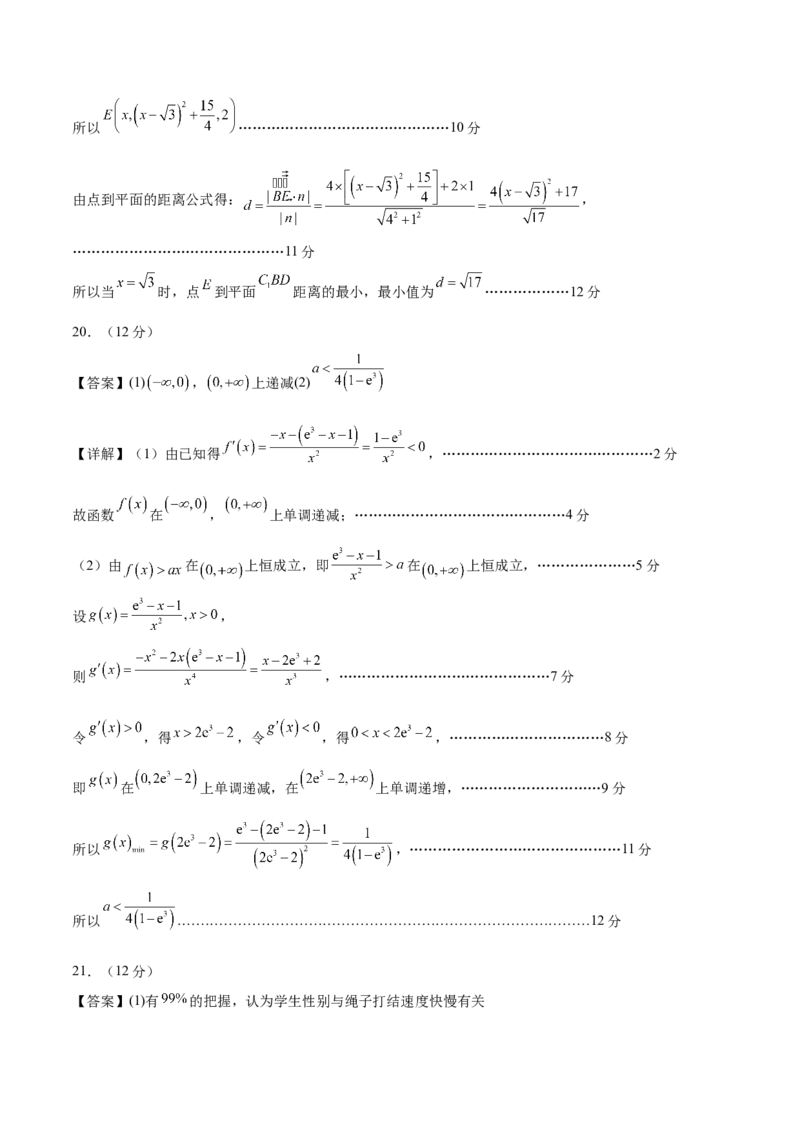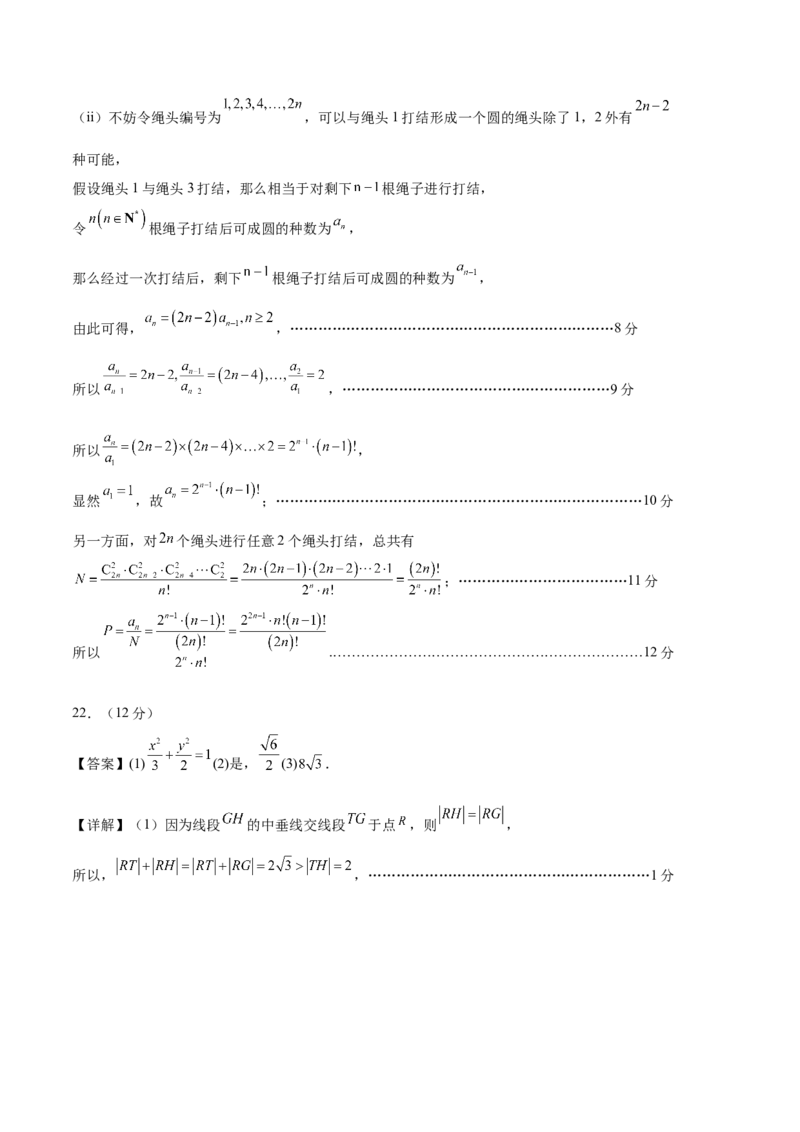文档内容
2024 年高考数学第一次模拟考试
数学(新高考 I 卷)·参考答案
第 I 卷(选择题)
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项
是符合要求的。
1 2 3 4 5 6 7 8
C C C B C A A D
二、多项选择题:本题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符
合题目的要求,全部选对的得5分,部分选对的得2分,有选错的得0分。
9 10 11 12
AB ABC ABD AC
第 II 卷(非选择题)
三、填空题:本题共4小题,每小题5分,共20分。
13. 14. 15. 16.16
四、解答题:本题共6小题,共70分,解答应写出必要的文字说明、证明过程及验算步骤。
17.(10分)
【答案】(1) (2)
(2)利用分组求和法计算可得.
【详解】(1)因为 , ,数列 为等比数列,
所以 , ,则 ,……………………………………1分
即 是以 为首项, 为公比的等比数列,…………………………………2分
所以 ,……………………………………………………………………3分
则 .……………………………………………………………5分(2)
…………………………………………6分
……………………………7分
.……………………………10分
18.(12分)
【答案】(1) (2)
【详解】(1)解法一:因为 ,由正弦定理得 ,……………1分
可得 ,即 ,……………………………………………………2分
又因为 ,由余弦定理得 ,即 ,………………3分
联立方程组 ,可得 ,即 ,所以 ,………………4分
由余弦定理定理得 ,………………………………5分
因为 ,所以 .………………………………………………………………6分
解法二:因为 ,由正弦定理得 ,…………1分
整理得 ,…………………2分
又因为 ,可得 ,所以 ,…………3分
即 ,可得 ,即 ,…………4分
因为 ,所以 ,……………………………5分
所以 ,所以 .………………………………………………………6分(2)由(1)知 ,可得 ,且 ,
所以 ,……………………………………………8分
由三角形三边关系,可得 ,可得 ,……………………………………………9分
令 ,可得 ,其中 ,……………………………………………10
分
所以函数 ,……………………………………………11分
所以 ,所以 的取值范围是 .……………………………………………12分
19.(12分)
【答案】(1)见详解;(2)存在点 使得 与平面 夹角的正弦值为 ,点 到平面 距
离的最小值为
【详解】(1)取 中点 ,连接 ,则 ,
所以四边形 是菱形, 是正三角形,
所以 , ,
因为 ,所以 ,
所以 ,所以 ,………………………………………2分
因为 底面 , 平面 ,
所以 ,……………………………………………………………3分
又因为 平面 , 平面 , ,所以 平面 ,因为 平面 ,………………………………………4分
所以平面 平面 ………………………………………5分
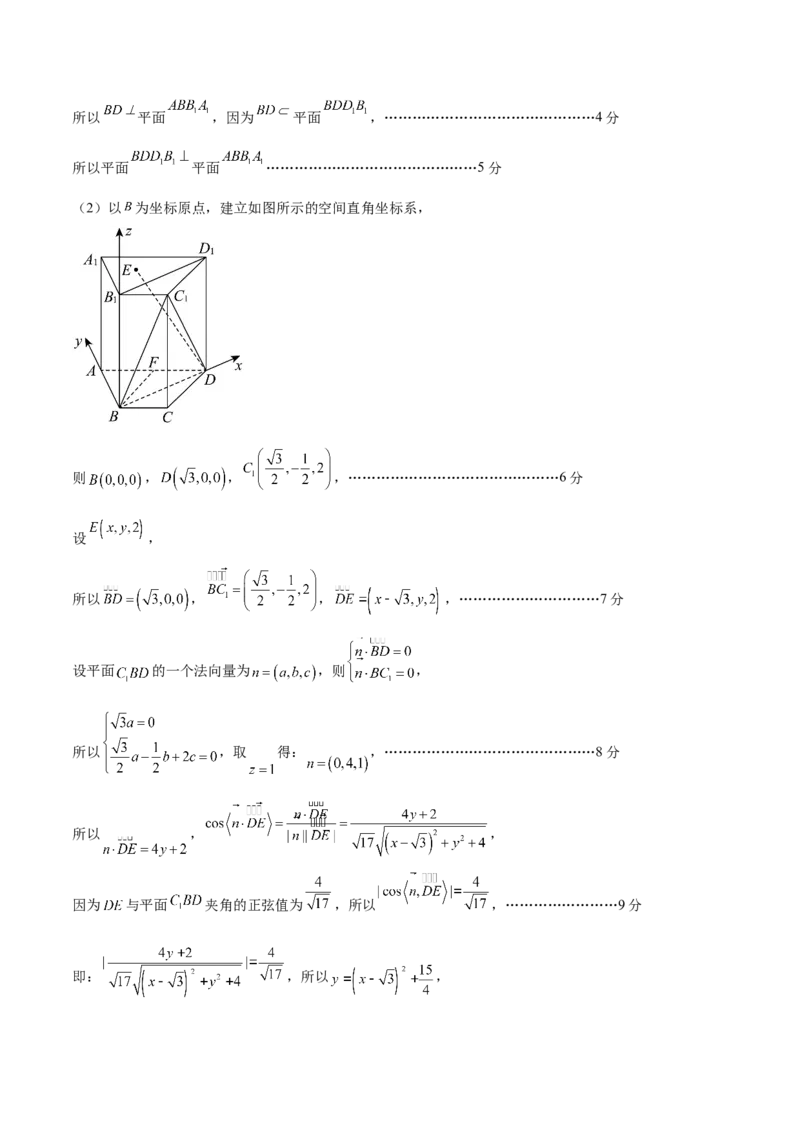
(2)以 为坐标原点,建立如图所示的空间直角坐标系,
则 , , ,………………………………………6分
设 ,
所以 , , ,…………………………7分
设平面 的一个法向量为 ,则 ,
所以 ,取 得: ,………………………………………8分
所以 , ,
因为 与平面 夹角的正弦值为 ,所以 ,……………………9分
即: ,所以 ,所以 ………………………………………10分
由点到平面的距离公式得: ,
………………………………………11分
所以当 时,点 到平面 距离的最小,最小值为 ………………12分
20.(12分)
【答案】(1) , 上递减(2)
【详解】(1)由已知得 ,………………………………………2分
故函数 在 , 上单调递减;………………………………………4分
(2)由 在 上恒成立,即 在 上恒成立,…………………5分
设 ,
则 ,………………………………………7分
令 ,得 ,令 ,得 ,……………………………8分
即 在 上单调递减,在 上单调递增,…………………………9分
所以 ,………………………………………11分
所以 .……………………………………………………………………………12分
21.(12分)
【答案】(1)有 的把握,认为学生性别与绳子打结速度快慢有关(2)(i)分布列见解析, ;(ii)证明见解析
【详解】(1)依题意,完善 列联表如下,
速度
性
合计
别
快 慢
男
65 35 100
生
女
45 55 100
生
合
110 90 200
计
………………………………………………………………1分
所以 .…………………………………2分
故有 的把握,认为学生性别与绳子打结速度快慢有关.…………………………3分
(2)(i)由题知,随机变量 的所有可能取值为 ,
………………………………………………………………4分
…………………………………………………5分
,……………………………………………………………6分
所以 的分布列为
1 2 3
所以 .…………………………………………………7分(ii)不妨令绳头编号为 ,可以与绳头1打结形成一个圆的绳头除了1,2外有
种可能,
假设绳头1与绳头3打结,那么相当于对剩下 根绳子进行打结,
令 根绳子打结后可成圆的种数为 ,
那么经过一次打结后,剩下 根绳子打结后可成圆的种数为 ,
由此可得, ,……………………………………………………………8分
所以 ,…………………………………………………9分
所以 ,
显然 ,故 ;……………………………………………………………………10分
另一方面,对 个绳头进行任意2个绳头打结,总共有
;………………………………11分
所以 .…………………………………………………………12分
22.(12分)
【答案】(1) (2)是, (3) .
【详解】(1)因为线段 的中垂线交线段 于点 ,则 ,
所以, ,……………………………………………………1分由椭圆定义知:动点 的轨迹为以 、 为焦点,长轴长为 的椭圆,
设椭圆方程为 ,则 , , , ,……………2分
所以曲线 的方程为 ………………………………………………………………3分
(2)设 , ,直线 : ;
, 到直线 的距离 ,
所以 ………………………………………5分
另一方面,因为 , 是椭圆 上的动点,
所以可设 , , ,
由 ,得 ,
为定值.……………………………………………………………6分
(3)设 , , ,代入 : 得 ,所以曲线 的方程为 .………………………7分
由 知 ,同理 , ,………………………8分
设 ,
①当直线 有斜率时,设 : ,
代入椭圆 的方程得: ,
, ,
…………………………………………………………………9分
将 : 代入椭圆 的方程得: ,
与椭圆 有公共点 , 由 得: ,
令 ,则 ,
.………………………………………………………………10分
②当 斜率不存在时,设 : ,代入椭圆 的方程得: ,,……………………………………………11分
综合①②得 面积的最大值为 ,
所以 面积的最大值为 .…………………………………………………………………12分