文档内容
2024~2025 学年第一学期第二次月考
高二数学(学科)试题
注意事项:
1.考试时间120分钟,试卷总分150分。
2.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
3.请用2B铅笔和0.5毫米黑色墨水签字笔在答题卡上指定区域内作答。
一、单选题
1.若集合A={−1,−2,−3},B={x+ y|x∈A,y∈A},则A∩B=( )
A. {−2} B. {−3} C. {−2,−3} D. {−1,−2,−3}
z−1
2.已知 =2−i,则z=( )
z+3
A. −2−2i B. −2+2i C. −5+2i D. −5−2i
2
3.点P在曲线y=x3−x+ 上,设曲线在点P处切线的倾斜角为α,则角α的取值范围是(
3
)
A. [ π) B. [ π) ( π ) C. [3π ) D.
0, 0, ∪ − ,0 ,π
2 2 2 4
[ π) [3π )
0, ∪ ,π
2 4
4.设递增等比数列{a }满足a +a =20,a a a =512,则a a +a a +…+a a =( )
n 4 6 4 5 6 1 2 2 3 n n+1
2n−1 2n+1−1 4n−1 4n+1−1
A. B. C. D.
2 2 6 6
5.已知函数 ,若 ,则实数 的取值范围为( )
f(x)=x3+2x−sinx f(2a2 )+f(a−1)≤0 aA. ( 1] B. [ 1 ]
−∞,− ∪[1,+∞) − ,1
2 2
C. [1 ) D. [ 1]
(−∞,−1]∪ ,+∞ −1,
2 2
6.已知圆C:x2+y2-2x+my+1=0(m∈R)关于直线x+2y+1=0对称,圆C 的标准方程是
1 2
(x+2)2+(y-3)2=16,则圆C 与圆C 的位置关系是( )
1 2
A.外离 B.外切 C.相交 D.内含
7.若直线y=4x+m是曲线y=x3−nx+13与曲线y=x2+2lnx的公切线,则n−m=( )
A. 11 B. 12 C. −8 D. −7
8.已知双曲线
x2 y2
的左、右焦点分别为 , ,点 在双曲线
C: − =1(a>0,b>0) F F P
a2 b2 1 2
x2 y2 上,点 在直线 上,且满足 ⃗ ⃗ ⃗ ⃗ 若存在实数 使
C: − =1 H x=a 2HP+3H F +4H F =0. λ
a2 b2 1 2
→ →
得
O
→
H=O
→
P+λ(
PF
1 +
PF
2 )
,则双曲线C的离心率为( )
sin∠PF F sin∠PF F
2 1 1 2
7 7
A. B. C. 2 D. 3
4 2
二、多选题
9.已知直线l:(2m+1)x+(m+1)y−7m−4=0,则下列结论正确的是( )
A. 直线l过定点(3,1)
B. 原点O到直线l距离的最大值为❑√10
1
C. 若点A(−1,0),B(1,0)到直线l的距离相等,则m=−
2
4 1
D. 若直线l经过一、二、三象限,则− 2
2n 2024 2023
C. S <−2015 D. S −S <2
2024 2024 2025
11.已知斜率为 的直线l经过抛物线 的焦点 ,与抛物线C交于A,B两点
(点A在第一象限),O为坐标原点,则下列结论正确的是( )
A. B. C. D.
三、填空题
12.已知平面向量 ⃗a=(2,m) , ⃗b=(1,−1) ,且
|
⃗
a+2
⃗
b|=|
⃗
a−2
⃗
b|
,则
|
⃗
a|=
13.已知圆C:x2+(y-1)2=5,直线l:mx-y+1-m=0.若定点P(1,1)分弦AB为AP∶PB
=1∶2,求直线l的方程 .
14.如图,在边长为a的等边三角形ABC中,圆D与△ABC相切,圆
1
D与圆D相切且与AB,AC相切,…,圆D 与圆D相切且与AB,AC
2 1 n+1 n
相切,依次得到圆D,D,…,D.设圆D,D,…,D的面积之和
3 4 n 1 2 n
为 ,( ),则
四、解答题
15.(本小题13分)
a2+b2−c2
△ABC的内角A,B,C的对边分别为a,b,c,已知(c−2b)cosA+ =0.
2b
(1)若a=4,b+c=8,求△ABC的面积;
c
(2)若角C为钝角,求 的取值范围.
b16.(本小题15分)
已知数列{a }的前n项和为S ,且n、a 、S 成等差数列,b =2log (1+a )−1.
n n n n n 2 n
(1)求数列{a }的通项公式;
n
(2)若数列{b }中去掉数列{a }的项后余下的项按原顺序组成数列{c },求
n n n
c +c +⋅⋅⋅+c 的值.
1 2 100
17.(本小题15分)
设函数 , .
f(x)=x2+ax−lnx a∈R
(1)当a=1时,求f(x)的单调区间.
令 ,是否存在实数 ,当 时,函数 的最小值是 ?若存
(2) g(x)=f(x)−x2 a x∈(0,e] g(x) 3
在,求出a的值;若不存在,说明理由.
18.(本小题17分)
已知数列 的前 项和为 ,且 .
{a } n S S =2a +n−3
n n n n
证明:数列 为等比数列,并求 的通项公式;
(1) {a −1} {a }
n n
在 和 之间插入 个数,使这 个数组成一个公差为 的等差数列,求数列{1 }
(2) a a n n+2 d
n n+1 n d
n
的前n项和T .
n若对于任意 ,数列{1 }的前 项和 恒成立,求实数 的取值范围.
(3) n∈N n T >m m
+ d n
n
19.(本小题17分)
已知椭圆x2 y2 的离心率为1,左、右焦点分别为 、 , 是椭圆上任一
+ =1(a>b>0) F F P
a2 b2 2 1 2
点,▵PF F 的面积的最大值为❑√3.
1 2
(1)求椭圆的标准方程;
(2)四边形ABCD的顶点在椭圆上,且对角线AC、BD过原点O,设A(x ,y ),B(x ,y ),
1 1 2 2
①若3x x =4 y y ,求证:直线AB和直线BC的斜率之和为定值;
1 2 1 2
②
若
O
⃗
A⋅O
⃗
B=0
,求四边形
ABCD
周长的取值范围.
一 单选
、 、 、 、 、 、 、 、
1 C 2 D 3 D 4 C 5 D 6 B 7 A 8 C
二多选
、ABD 、 ACD 、
9 10 11 AD三填空
12、2❑√2 13、x-y=0或x+y-2=0. 14、
四解答题
、【答案】解:(1)根据题意得 (c−2b)cosA+acosC=0 ,
1由5正弦定理得 (sinC−2sinB)cosA+sin AcosC=0 ,
因为 sinCcosA+sin AcosC=sin(A+C)=sin(π−B)=sinB ,
1
所以 sinB(1−2cosA)=0 ,因为 00,所以cosA= ,
2
π
又 0
3 2
❑√3 ❑√3 3 c c
则 0 ,即 >2 ,故 的取值范围是 (2,+∞) .
3 2tanB 2 b b
、
16【答案】解:(1)因为n,a ,S 成等差数列,
n n
所以S +n=2a ,①
n n
所以 由 ,得 ,
S +n−1=2a (n≥2)② ①−② a +1=2a −2a
n−1 n−1 n n n−1
所以a +1=2(a +1)(n≥2),又当n=1时,S +1=2a ,所以a =1,所以a +1=2,
n n−1 1 1 1 1
故数列 是首项为 ,公比为 的等比数列,所以 ,
{a +1} 2 2 a +1=2⋅2n−1=2n
n n
即 ;
a =2n−1
n
据 求解知, , ,
(2) (1) b =2log (1+2n−1)−1=2n−1 b =1
n 2 1
所以b −b =2,所以数列{b }是以1为首项,2为公差的等差数列,
n+1 n n
又因为a =1,a =3,a =7,a =15,a =31,
1 2 3 4 5
a =63,a =127,a =255,b =127,b =211,b =213,
6 7 8 64 106 107
所以c +c +…+c =(b +b +…+b )−(a +a +…+a )
1 2 100 1 2 107 1 2 7
107×(1+213) 107×214 2(1−27 )
= −[(21+22+…+27 )−7]= − +7
2 2 1−2
=1072−28+9=11202.
、【答案】解: 当 时, , ,得
(1) a=1 f(x)=x2+x−lnx x>0
17
1 (2x−1)(x+1) 1
f '(x)=2x+1− = , 令f '(x)>0,解得x> ,令f '(x)<0,解得
x x 2
1
00 g(x) ,e g(x) (0,e]
a
(1) ,解得 ,满足题意;
g =1+lna=3 a=e2
a
1
③当 ≥e时,x∈(0,e)时,g'(x)<0,g(x)在(0,e]上单调递减, 所以g(x)在(0,e]
a
4
上的最小值为g(e)=ae−1=3,解得a= ,不合题意,舍去.
e
综上,存在实数a=e2,使得当x∈(0,e]时,g(x)的最小值是3.
、【答案】解:(1)因为S =2a +n−3,①当n=1时,a =2a −2,所以a =2.
n n 1 1 1
1当8 时, , 由 得 ,即 ,
n≥2 S =2a +n−4 ② ①−② a =2a −2a +1 a =2a −1
n−1 n−1 n n n−1 n n−1
所以a −1=2(a −1),又a −1=1,
n n−1 1
所以数列 是首项为 ,公比为 的等比数列,
{a −1} 1 2
n所以 ,当 时, 也适合 ,
a −1=2n−1 n=1 a =2 a −1=2n−1
n 1 n
故 的通项公式为 ;
{a } a =2n−1+1
n n
因为 ,所以 ,
(2) a =a +(n+1)d 2n+1=2n+1+1+(n+1)d
n+1 n n n
2n−1 1 n+1 2 3 4 n+1
解得d = ,所以 = .所以T = + + +⋯+ ,
n n+1 d 2n−1 n 20 21 22 2n−1
n
1 2 3 4 n n+1
T = + + +⋯+ + ,
2 n 21 22 23 2n−1 2n
两式相减得1
T =2+
( 1
+
1
+
1
+⋯+
1 )
−
n+1
2 n 21 22 23 2n−1 2n
1[ (1) n−1]
1−
2 2 n+1 n+3.
=2+ − =3−
1 2n 2n
1−
2
n+3
所以T =6− ;
n 2n−1
n+3 n+3
(3)由于对于任意n∈N ,T >m恒成立,即6− >m恒成立,等价于6− 的
+ n 2n−1 2n−1
n+3 n+4 n+3 −n−2 n+2
最小值大于m.令b = ,则b −b = − = =− <0,
n 2n−1 n+1 n 2n 2n−1 2n 2n
1+3
所以数列{b }是递减数列,故数列{b }中的最大值为b = =4,
n n 1 21−1
所以T 的最小值为2,所以当T >m对于任意n∈N 恒成立时,m<2.
n n +c 1 1
、【答案】解:(1)由题意e= = , ×2c×b=cb=❑√3,
a 2 2
19
x2 y2
又a2=b2+c2,解得a=2,b=❑√3,所以椭圆的标准方程为: + =1;
4 3
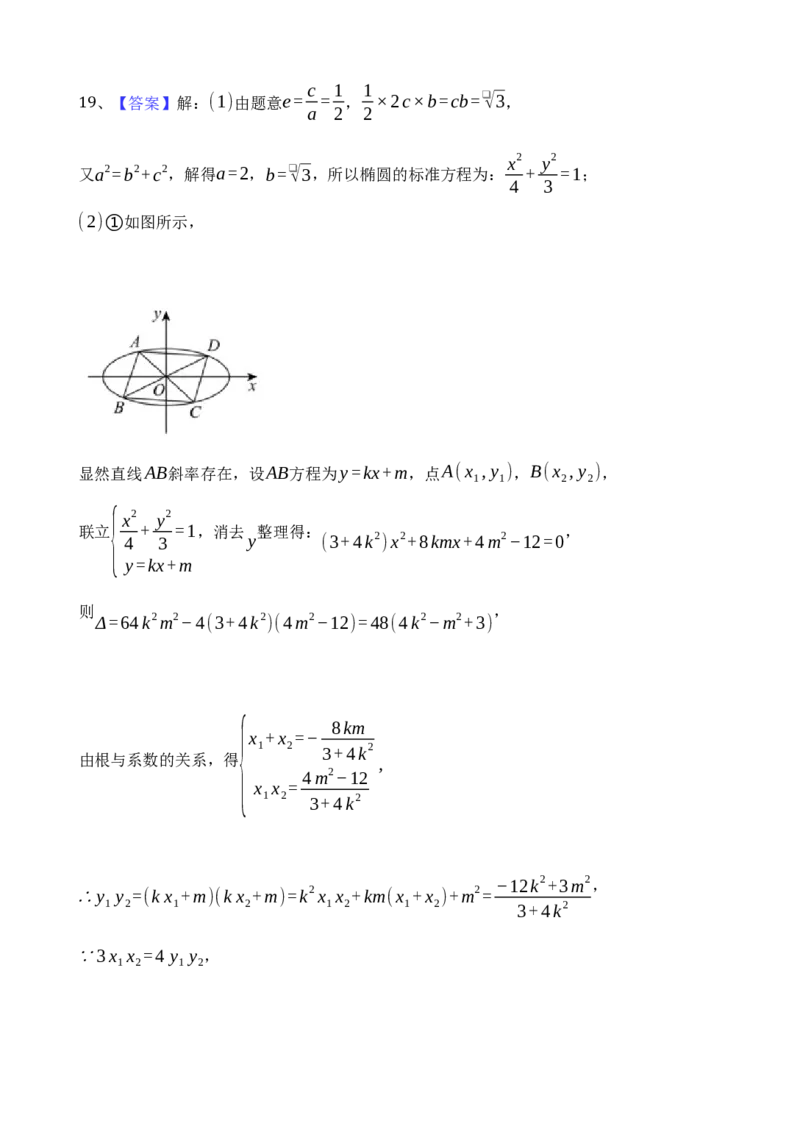
(2)①如图所示,
显然直线AB斜率存在,设AB方程为y=kx+m,点A(x ,y ),B(x ,y ),
1 1 2 2
{x2 y2
联立 + =1,消去 整理得: ,
4 3 y (3+4k2 )x2+8kmx+4m2−12=0
y=kx+m
则 ,
Δ=64k2m2−4(3+4k2 )(4m2−12)=48(4k2−m2+3)
8km
{x +x =−
1 2 3+4k2
由根与系数的关系,得 ,
4m2−12
x x =
1 2 3+4k2
−12k2+3m2,
∴y y =(kx +m)(kx +m)=k2x x +km(x +x )+m2=
1 2 1 2 1 2 1 2 3+4k2
∵3x x =4 y y ,
1 2 1 24m2−12 −12k2+3m2,解得 ,
∴3· =4· 4k2−3=0
3+4k2 3+4k2
又 y + y 2m 3 , 3 4k2−3 ,
∵k = 2 1=k+ =− k +k =k− = =0
BC x +x x +x 4k AB BC 4k 4k
2 1 2 1
所以直线AB和直线BC的斜率之和为定值0;
因为对角线 、 过原点 ,且 ⃗ ⃗ ,即 ,
② AC BD O OA⋅OB=0 OA⊥OB
所以四边形ABCD为菱形,所以四边形ABCD的周长为:4|AB|,
若直线AB斜率不存在,则设A(x ,y ),则B(x ,−y ),因为⃗OA⋅⃗OB=0,所以
0 0 0 0
|x |=|y |,
0 0
所以x2 y2 ,所以 2❑√21,所以 4❑√21,
0+ 0=1 |y |= |AB|=2|y |=
4 3 0 7 0 7
16❑√21
所以四边形ABCD周长为 ;
7
若直线AB斜率存在,设AB方程为y=kx+m,
于是
⃗ ⃗ 4m2−12 8km
OA⋅OB=x x + y y =(k2+1)x x +km(x +x )+m2=(k2+1) −km· +m2=0
1 2 1 2 1 2 1 2 3+4k2 3+4k2
化简得7m2=12k2+12,
故 |AB|=❑√k2+1|x −x |=❑√k2+1 ❑√48(4k2−m2+3) = 4❑√21 ❑ √(k2+1)(16k2+9),
1 2 3+4k2 7 (3+4k2 ) 2
t+1
令3+4k2=t(t≥3),则k2+1= ,16k2+9=4t−3,
4所以 4❑√21 √(t+1)(4t−3) 2❑√21 √ 1 3 2❑√21 √ 1 1 49,
|AB|= ❑ = ❑4+ − = ❑−3( − ) 2+
7 4t2 7 t t2 7 t 6 12
1 1 1 1 4❑√21 1 1
因为 ∈(0, ],所以当 = 时,|AB| = ,当 = 时,|AB| =❑√7,
t 3 t 3 min 7 t 6 max
4❑√21
综上,|AB|的取值范围为[ ,❑√7],
7
16❑√21
所以,四边形ABCD周长的取值范围是[ ,4❑√7].
7