文档内容
2024 年高考数学第一次模拟考试
数学(新高考Ⅱ卷)·全解全析
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.答卷前,考生务必将自己的姓
名、准考证号填写在答题卡上.
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如
需改动,用橡皮擦干净后,再选涂其他答案标号.写在本试卷上无效.
3.回答第Ⅱ卷时,将答案写在答题卡上.写在本试卷上无效.
4.测试范围:高考全部内容
5.考试结束后,将本试卷和答题卡一并交回.
第 I 卷(选择题)
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项
是符合要求的。
1.设全集U=R,集合A={x||x-2|≥1},B=¿,则(∁ A)∪B=( )
U
A.{x|-30),利用两点间距离公式可得
4
|PF| √ (4 4) 2 9
=❑ - + ,结合二次函数性质可得解.
|PO| t 5 25
3
【详解】由题意,F(5,0),双曲线的渐近线为y=± x,
4
( 3 )
由点P在第一象限,可设P t, t (t>0),
4
则|PO|= 5 t,|PF|=❑ √ (t-5) 2+ (3 t ) 2 =❑ √25 t2-10t+25,
4 4 16
|PF| √ 32 16 √ (4 4) 2 9
所以 =❑1- + =❑ - + ,
|PO| 5t t2 t 5 25
|PF|
所以当t=5时, 取最小值,
|PO|
( 15)
此时P 5, ,
4
1 1 15 75
此时△POF的面积S = |OF|⋅y = ×5× = ,
△POF 2 p 2 4 8
故选:C.
1
7.在△ABC中,⃗BD= ⃗BC,E是线段AD上的动点(与端点不重合),设⃗CE=x⃗CA+ y⃗CB,
3
2x+3 y
则 的最小值是( )
3xy
A.3 B.1 C.2 D.4
【答案】D
3
【分析】由已知条件结合平面向量基本定理可得x+ y=1,x>0,y>0,则
22x+3 y 2 1 ( 2 1)( 3 ),化简后利用基本不等式可求得结果
= + = + x+ y
3xy 3 y x 3 y x 2
【详解】
1 3
因为⃗BD= ⃗BC,所以⃗CB= ⃗CD,
3 2
3
因为⃗CE=x⃗CA+ y⃗CB,所以⃗CE=x⃗CA+ y⃗CD,
2
3
因为A,D,E三点共线,所以x+ y=1,x>0,y>0,
2
2x+3 y 2 1 ( 2 1)( 3 )
所以 = + = + x+ y
3xy 3 y x 3 y x 2
2x 3 y √2x 3 y 2x 3 y 1 1
= +1+1+ ≥2❑ ⋅ +2=4,当且仅当 = ,即x= 、y= 时取等号,
3 y 2x 3 y 2x 3 y 2x 2 3
2x+3 y
所以 的最小值是4.
3xy
故选:D
1
8.已知a= ,b=log 2,c=sin(cos1.1),则( )
√
3e 3
A.b ,结合对数函数单调性得到log 2∈ , ,比较出大小.
3 3 2 3π π
【详解】因为1.1> ,而y=cosx在x∈ ( 0, ) 上单调递减,
3 2
π 1
故cos1.10在x∈ ( 0, ) 上恒成立,
2
π
( )
故f (x)=x-sinx在x∈ 0, 上单调递增,f (x)>f (0)=0,
2
(1) 1 1
故f >0,即 >sin ,
2 2 2
1 1
故c=sin(cos1.1)g(0)=0,故e 3> ,
3 3
1 1 2
因为23<32,所以 (23)3<(32)3,即 2<33,
因为y=log x在(0,+∞)上单调递增,
3
2
故log 2< ,
3 3
1 (1 2)
又log 2>log ❑√3= ,故log 2∈ , ,
3 3 2 3 2 3
故c ,
❑√2 2
1
所以圆C上有4个点到直线的距离为 ,故C正确;
2
当k=1时,直线l:x- y=0,曲线E:x2+ y2-(λ+4)x+λy=0,
即x2+ y2-4x-λ(x- y)=0一定过直线l:x- y=0与圆C:x2+ y2-4x=0的交点,故D正确.
故选:BCD.
1 11 7
10.设A,B是一个随机试验中的两个事件,且P(A)= ,P(B)= ,P(AB+AB)= ,则
2 24 24
下列结论中正确的是( )
1 5
A.P(AB)= B.P(A+B)=
8 6
9
C.P(A|B)= D.P(A|B)=P(B|A)
11
【答案】AB
【分析】利用和事件的概率公式和条件概率公式求解即可.1 11 1 13
【详解】因为P(A)= ,P(B)= ,所以P(A)= ,P(B)=
.
2 24 2 24
因为AB与AB为互斥事件,所以P(AB⋅AB)=0,
所以P(AB+AB)=P(AB)+P(AB)-P(AB⋅AB)=P(AB)+P(AB)
1 11 7
=P(B)-P(AB)+P(A)-P(AB) = + -2P(AB) = ,
2 24 24
1
所以P(AB)= ,
3
11 1 1
故P(AB)=P(B)-P(AB)= - = ,故A正确;
24 3 8
1 1 5
P(A+B)=P(A)+P(B)-P(AB)=P(A)+P(B)-[P(B)-P(AB)]=P(A)+P(AB)= + =,
2 3 6
故B正确;
1
P(AB) 3 8
P(A|B)= = = ,故C错误;
P(B) 11 11
24
1 1 1
-
P(AB) 8 3 P(AB) P(A)-P(AB) 2 3 1
P(A|B)= = = ,P(B|A)= = = = ,
P(B) 11 11 P(A) P(A) 1 3
24 2
所以P(A|B)≠P(B|A),故D错误.
故选:AB.
11.在正方体ABCD-A B C D 中,AB=1,点P满足⃗CP=λ⃗CD+μ⃗CC ,其中
1 1 1 1 1
λ∈[0,1],μ∈[0,1],则下列结论正确的是( )
π
A.当B P//平面A BD时,B P与CD 所成夹角可能为
1 1 1 1 3
❑√2+❑√5
B.当λ=μ时,|⃗DP|+|⃗A P|的最小值为
1 2
π π
C.若B P与平面CC D D所成角为 ,则点P的轨迹长度为
1 1 1 4 2
[❑√3 ]
D.当λ=1时,正方体经过点A ,P,C的截面面积的取值范围为 ,❑√2
1 2
【答案】ACπ
【分析】A选项,当点P与点D 重合时,满足B P//平面A BD,B P与CD 所成夹角为 ,A
1 1 1 1 1 3
正确;B选项,将两图形展开到同一平面内,由三点共线得到|⃗DP|+|⃗A P|的最小值,由余弦
1
定理求出最小值;C选项,作出辅助线,得到点P的轨迹,求出轨迹长度;D选项,先得到点P在
线段DD 上,从而得到正方体过点A ,P,C的截面,建立空间直角坐标系,得到点P到直线A C
1 1 1
的距离,从而求出截面面积的取值范围.
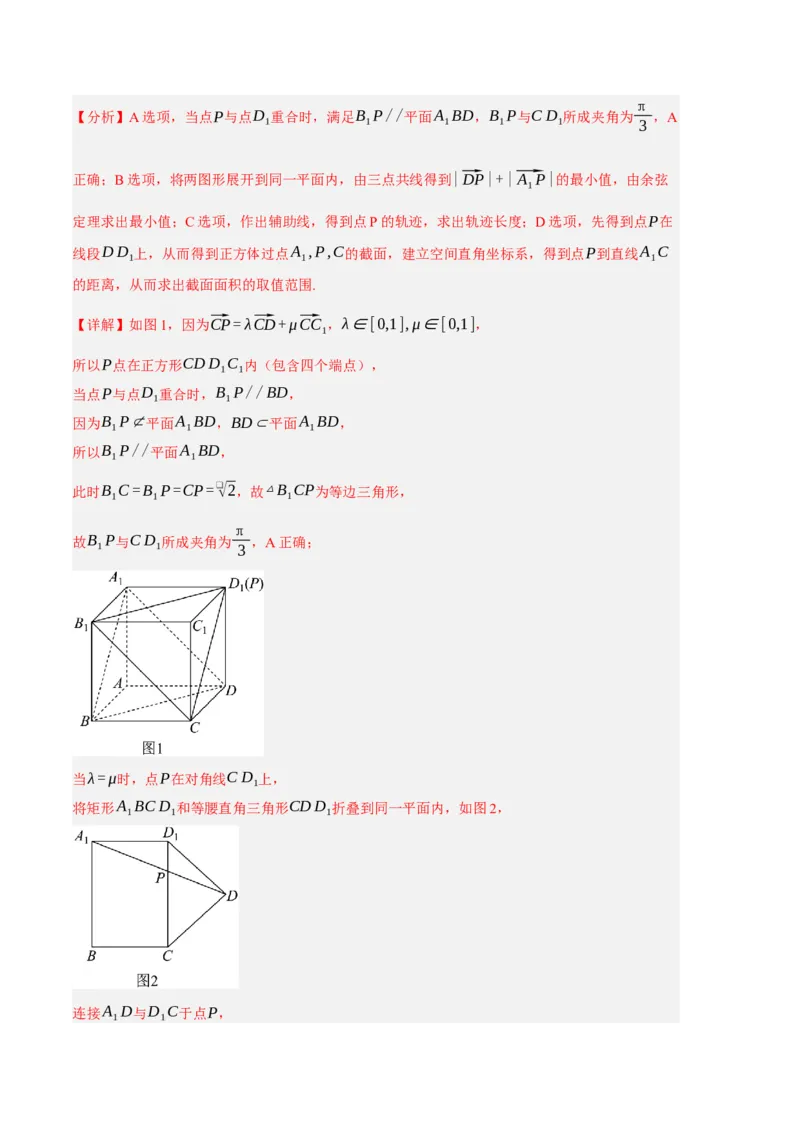
【详解】如图1,因为⃗CP=λ⃗CD+μ⃗CC ,λ∈[0,1],μ∈[0,1],
1
所以P点在正方形CDD C 内(包含四个端点),
1 1
当点P与点D 重合时,B P//BD,
1 1
因为B P⊄平面A BD,BD⊂平面A BD,
1 1 1
所以B P//平面A BD,
1 1
此时B C=B P=CP=❑√2,故△B CP为等边三角形,
1 1 1
π
故B P与CD 所成夹角为 ,A正确;
1 1 3
当λ=μ时,点P在对角线CD 上,
1
将矩形A BCD 和等腰直角三角形CDD 折叠到同一平面内,如图2,
1 1 1
连接A D与D C于点P,
1 1由三点共线可知,|⃗DP|+|⃗A P|的最小值即为A D的长,
2 1
其中A D =D D=1,∠A D D=135°,
1 1 1 1 1
由余弦定理得
A D=❑√A D2+D D2-2A D ⋅D Dcos135°=❑ √ 1+1-2× ( - ❑√2) =❑√2+❑√2,B错误;
1 1 1 1 1 1 1 2
1
C选项,如图3,以C 为圆心,CC 的长为半径作圆,与正方形CDD C 交于 圆弧,
1 1 1 1 4
π
此时满足B P与平面CC D D所成角为 ,
1 1 1 4
1 π
故则点P的轨迹长度等于 ×2π×1= ,C正确;
4 2
D选项,如图4,当λ=1时,⃗CP=⃗CD+μ⃗CC ,即⃗CP-⃗CD=μ⃗CC ,故⃗DP=μ⃗CC ,
1 1 1
故点P在线段DD 上,
1
在BB 上取点H,使得B H=PD,连接A H,CH,
1 1 1
则可证得A H=PC,CH=A P,四边形A PCH为平行四边形,
1 1 1
故正方体经过点A ,P,C的截面为平行四边形A PCH,
1 1
以A为坐标原点,AB,AD,A A 所在直线分别为x,y,z轴,建立空间直角坐标系,
1
则A (0,0,1),C(1,1,0),P(0,1,μ),μ∈[0,1],
1
⃗A C (1,1,-1) (❑√3 ❑√3 ❑√3)
其中⃗m= 1 = = , ,- ,⃗A C=(1,1,0)-(0,0,1)=(1,1,-1),
|⃗A C| ❑√1+1+1 3 3 3 1
1
⃗PA =(0,0,1)-(0,1,μ)=(0,-1,1-μ),
1(❑√3 ❑√3 ❑√3) ❑√3 ❑√3 ❑√3 ❑√3 2❑√3
则⃗PA ⋅⃗m=(0,-1,1-μ)⋅ , ,- =- - + μ= μ- ,
1 3 3 3 3 3 3 3 3
则点P到直线A C的距离d=❑√⃗PA 2-(⃗PA ⋅⃗m) 2 =❑
√
1+(1-μ) 2-
(❑√3
μ-
2❑√3) 2
1 1 1 3 3
√2( 1) 2 1
=❑ μ- + ,
3 2 2
√2( 1) 2 1 [❑√2 ❑√6]
因为μ∈[0,1],所以d=❑ μ- + ∈ , ,
3 2 2 2 3
[❑√6 ]
故截面面积为d⋅|⃗A C|=❑√3d∈ ,❑√2 ,D错误.
1 2
故选:AC
【点睛】方法点睛:立体几何中截面的处理思路:
(1)直接连接法:有两点在几何体的同一个平面上,连接该两点即为几何体与截面的交线,找截
面就是找交线的过程;
(2)作平行线法:过直线与直线外一点作截面,若直线所在的平面与点所在的平面平行,可以通
过过点找直线的平行线找到几何体与截面的交线;
(3)作延长线找交点法:若直线相交但在立体几何中未体现,可通过作延长线的方法先找到交点,
然后借助交点找到截面形成的交线;
(4)辅助平面法:若三个点两两都不在一个侧面或者底面中,则在作截面时需要作一个辅助平面.
12.已知函数f(x)=x2-8x+6lnx,且函数g(x)=f(x)-m有三个零点x ,x ,x (x 2
1 2
【答案】ABD
【分析】求出导数,研究函数f(x)的单调性及极值可能判断A、B两项,由导数的几何意义可以
判断C项,构造函数F(x)=f(x)-f(2-x),x∈(0,1),可以判断D项.
【详解】解:对于A,由题设得,函数f(x)的定义域为(0,+∞),且
6 2(x-1)(x-3)
f' (x)=2x-8+ = .
x x
当x∈(0,1)∪(3,+∞)时,f' (x)>0;当x∈(1,3)时,f' (x)<0.
所以f(x)的单调递增区间为(0,1),(3,+∞),单调递减区间为(1,3),故A正确.
对于B,因为函数f(x)在(0,1)上单调递增,在(1,3)上单调递减,在(3,+∞)上单调递增,
所以f(x)的极大值为f(1)=1-8+0=-7,极小值为f (3)=9-24+6ln3=-15+6ln3.
当x趋向于0时,f(x)趋向负无穷,当x趋向于正无穷时,f(x)趋向于正无穷.
由于函数g(x)=f(x)-m有三个零点,因此6ln3-150在(0,1)上恒成立,即F(x)=f(x)-f(2-x)在(0,1)上单调递增,
所以F(x)2-x ,即x +x >2,故D正确.
2 1 1 2
故选:ABD.第 II 卷(非选择题)
三、填空题:本题共4小题,每小题5分,共20分。
13.若 ( √3 x- 1) n 的展开式的二项式系数之和为16,则 ( √3 x+ 1) 2n 的展开式中 1 的系数为 .
x x x4
【答案】56
【分析】通过二项式系数和求出n=4,然后求出 ( √3 x+ 1) 8 展开式的通项公式,最后求出指定项的
x
系数即可.
【详解】由 ( √3 x- 1) n 的展开式的二项式系数之和为16,得2n=16,所以n=4,
x
则 ( √3 x+ 1) 8 的展开式的通项公式为T =Cr(√3 x) 8-r(1) r =Crx 8- 3 4r ,
x r+1 8 x 8
令 8-4r =-4,解得r=5,故 ( √3 x+ 1) 2n 的展开式中 1 的系数为C5=56.
3 x x4 8
故答案为:56
14.抛物线y2=2px(p>0)的焦点为F,准线为l,A,B是抛物线上的两个动点,且满足
2|MN|
⃗AF⋅⃗FB=0.设线段AB的中点M在l上的投影为N,则 的最大值是 .
3|AB|
❑√2
【答案】
3
1
【分析】根据抛物线的定义和几何性质,可得|AB| 2=|AF| 2+|BF| 2 ,|MN|= (|AF|+|BF|),可得
2
2|MN| ❑√2
2 2
|AB| ≥2|MN|,进而可得 的最大值为 .
3|AB| 3【详解】
如图,过A点作AC⊥l,过B作BD⊥l,设|AF|=m,|BF|=n,
则由抛物线的定义知|BD|=|BF|=n,|AC|=|AF|=m,
1 1
由题意知|MN|= (|BD|+|AC|)= (m+n),
2 2
因⃗AF⋅⃗FB=0得AF⊥BF,
|AB|
2=|AF| 2+|BF| 2=m2+n2,
(m+n) 2
因m2+n2≥ ,当且仅当m=n,即|AF|=|BF|时等号成立,
2
|MN| ❑√2
所以|AB| 2 ≥2|MN| 2 , ≤ ,
|AB| 2
2|MN| ❑√2
所以 ≤ ,
3|AB| 3
❑√2
故答案为:
3
15.分形几何学是一门以不规则几何形态为研究对象的几何学.分形的外表结构极为复杂,但其内
部却是有规律可寻的.一个数学意义上分形的生成是基于一个不断迭代的方程式,即一种基于递归
的反馈系统.下面我们用分形的方法来得到一系列图形,如图1,线段AB的长度为a,在线段AB
1
上取两个点C,D,使得AC=DB= AB,以CD为一边在线段AB的上方做一个正六边形,然后
4
去掉线段CD,得到图2中的图形;对图2中的最上方的线段EF作相同的操作,得到图3中的图形;
依此类推,我们就得到了以下一系列图形:记第n个图形(图1为第1个图形)中的所有线段长的和为S ,现给出有关数列{S }的四个命题:
n n
①数列{S }是等比数列;
n
②数列{S }是递增数列;
n
③存在最小的正数a,使得对任意的正整数n ,都有S >2018 ;
n
④存在最大的正数a,使得对任意的正整数n,都有S <2018.
n
其中真命题的序号是 (请写出所有真命题的序号).
【答案】②④
【分析】通过分析图1到图4,猜想归纳出其递推规律,再判断该数列的性质,即可求解.
【详解】由题意,得图1中线段为a,即S =a;
1
a a
图2中正六边形边长为 ,则S =S + ×4=S +2a;
2 2 1 2 1
a a
图3中的最小正六边形边长为 ,则S =S + ×4=S +a;
4 3 2 4 2
a a a
图4中的最小正六边形边长为 ,则S =S + ×4=S + ;
8 4 3 8 2 2
a
由此类推,S -S = ,
n n-1 2n-1
所以{S }为递增数列,但不是等比数列,即①错误,②正确;
n
a a
因为S =S +(S -S )+(S -S )+⋯+(S -S )=a+2a+a+ +⋯+
n 1 2 1 3 2 n n-1 2 2n-3
1
2a(1- )
2n-1 1
=a+ =a+4a(1- )<5a,
1 2n-1
1-
2
2018
即存在最大的正数a= ,使得对任意的正整数n,都有S <2018,
5 n即④正确;③错误,
综上可知正确的由②④.
【点睛】用数列知识解相关的实际问题,关键是列出相关信息,合理建立数学模型——数列模型,
判断是等差数列还是等比数列模型;求解时,要明确目标,搞清是求和、求通项、还是解递推关系
问题,所求结论对应的是解方程问题、解不等式问题、还是最值问题,然后经过数学推理与计算得
出的结果,放回到实际问题中进行检验,最终得出结论.
16.已知函数f (x)=¿,若存在m∈(2,8),使得方程f (x)=m-9有两个不同的实数根且两根之和
为6,则实数k的取值范围是 .
【答案】(❑√2,2❑√2)
【分析】先通过对题目的分析,令g(x)=f (x)+9,将题目简单化,并转化为等价形式;再根据函
数y=g(x)与y=m的图象有两个交点,数形结合可判断k>0;最后结合图形分析得出y=k(x-3)
与y=(x-3) 2 (x>3)图象的交点纵坐标与之间的关系: y =m∈(2,8),建立不等式求解即可得出
P
答案.
【详解】令g(x)=f (x)+9,得g(x)=¿,
则原问题等价于存在m∈(2,8),
使得y=g(x)与y=m的图象有两个交点且两交点的横坐标之和为6,
则k>0,作出函数y=g(x)与y=m的图象如图所示,
设两图象交点的横坐标分别为x ,x ,则x +x =6,
1 2 1 2
故两个交点关于二次函数y=(x-3) 2的图象的对称轴x=3对称,
设点P为y=k(x-3)与y=(x-3) 2 (x>3)图象的交点,且y =m∈(2,8),
P
联立y=k(x-3)与y=(x-3) 2 (x>3),解得x =k+3,故y =k2 ,
P P
故¿,解得❑√20,解得0b>0)的离心率为 ,且过点 -❑√3,- .
a2 b2 2 2
(1)求椭圆C的标准方程.
(2)已知过右焦点F的直线l与C交于A,B两点,在x轴上是否存在一个定点P,使∠OPA=∠OPB?
若存在,求出定点P的坐标;若不存在,请说明理由.
x2 y2
【答案】(1) + =1
12 3
(2)存在,P(4,0)
❑√3 ( 3)
【分析】(1)由离心率 与定点 -❑√3,- 代入椭圆方程,建立方程组a,b,c待定系数即可;
2 2
(2)由∠OPA=∠OPB条件转化为k +k =0,设直线l的方程为
PA PB
x=my+3,A(x ,y ),B(x ,y ),将斜率坐标化,利用韦达定理代入,得到t,m的等式,不论m如
1 1 2 2
何变化,等式恒成立求t值即可.
c √ b2 ❑√3
【详解】(1)因为e= =❑1- = ,所以a=2b.
a a2 2
x2 y2
所以椭圆C的方程为 + =1.
4b2 b2
9
( 3)
因为点 -❑√3,- 在椭圆C上,所以 3 4 ,解得b2=3,
2 + =1
4b2 b2
所以a2=12.
x2 y2
所以椭圆C的标准方程为 + =1.
12 3
(2)存在定点P(4,0),使∠OPA=∠OPB.理由如下:
由(1)知,c2=12-3=9,则点F(3,0).
设在x轴上存在定点P(ι,0),使∠OPA=∠OPB成立.
当直线l斜率为0时,直线右焦点F的直线l即x轴与C交于长轴两端点,
若∠OPA=∠OPB,则t>2❑√3,或t<-2❑√3.当直线l斜率不为0时,设直线l的方程为x=my+3,A(x ,y ),B(x ,y ),.
1 1 2 2
由¿消去x并整理,得(4+m2)y2+6my-3=0,
6m 3
则y + y =- ,y y =-
.
1 2 4+m2 1 2 4+m2
因为∠OPA=∠OPB,所以k +k =0,
PA PB
y y
所以 1 + 2 =0,即y (x -t)+ y (x -t)=0.
x -t x -t 1 2 2 1
1 2
所以y (m y +3-t)+ y (m y +3-t)=0,
1 2 2 1
即2m y y +3(y + y )-t(y + y )=0,
1 2 1 2 1 2
6m 18m 6mt 6m(t-4)
- - + = =0恒成立,
4+m2 4+m2 4+m2 4+m2
6m(t-4)
即对∀m∈R, =0恒成立,则t=4,即P(4,0).
4+m2
又点P(4,0)满足条件t>2❑√3.
综上所述,故存在定点P(4,0),使∠OPA=∠OPB.
ex
22.(12分)已知f (x)= ,g(x)=asinx,直线l 是y=f (x)在x=1处的切线,直线l 是
x 1 2
y=g(x)在x=0处的切线,若两直线l 、l 夹角的正切值为2,且当x>0时,直线l 恒在函数
1 2 2
y=g(x)图象的下方.
(1)求a的值;
(2)设F(x)=f (x)+g(x),若x 是F(x)在(-π,0)上的一个极值点,求证:x 是函数F(x)在
0 0上的唯一极大值点,且 .
(-π,0) 00时,直线l 恒在函数
1 2 2
y=g(x)图象的下方进行检验,即可得出实数a的值;
ex
(2)求得F(x)= -2sinx,x∈(-π,0),利用导数分析函数F(x)在(-π,0)上的单调性,结
x
合零点存在定理可证得x 是函数F(x)在(-π,0)上的唯一极大值点,再结合函数F(x)的单调性可
0
证得0φ(0)=0,满足题意.
综上所述,a=-2.
ex
(2)证明:由(1)知a=-2,故F(x)= -2sinx,x∈(-π,0).
x
(x-1)ex-2x2cosx
F'(x)=
,
x2
当x∈ [ - π ,0 ) 时,(x-1)ex<0,x2cosx≥0,F'(x)<0,
2故F(x)在 [ - π ,0 ) 上单调递减,
2
π π
当x∈ (-π,- ) 时,令h(x)=(x-1)ex-2x2cosx,x∈ (-π,- ) ,
2 2
h'(x)=xex-4xcosx+2x2sinx=x(ex-4cosx+2xsinx),
π
ex>0,cosx<0,xsinx>0,则h'(x)<0,故h(x)在 (-π,- ) 上单调递减,
2
因为h(-π)=2π2- π+1 >0,h (- π )=(- π -1 )e - π 2 <0,则h(-π)h (- π )<0,
eπ 2 2 2
π
由零点存在性定理知:h(x)在
(-π,- )
上有唯一零点,
2
π
即F'(x)在 (-π,- ) 上有唯一零点,该零点即为x ,
2 0
当x∈(-π,x )时,h(x)>0,即F'(x)>0,
0
π
当x∈ ( x ,- ) 时,h(x)<0,即F'(x)<0,
0 2
又x∈ [ - π ,0 ) 时,F'(x)<0,故F(x)在(-π,x )单调递增,在(x ,0)单调递减,
2 0 0
π
( )
则当x∈ (-π,- π ) 时,F(x )>F (- π )=2- 2 = 2 πe2 -1 >0,
2 0 2 π π
πe2 πe2
因为x ∈ (-π,- π ) ,则F(x )= ex 0 -2sinx <-2sinx <2,
0 2 0 x 0 0
0
故x 是函数F(x)在(-π,0)上的唯一的极大值点,且0g(x)(或f (x)0(或
f (x)-g(x)<0),进而构造辅助函数h(x)=f (x)-g(x);
(2)适当放缩构造法:一是根据已知条件适当放缩;二是利用常见放缩结论;
(3)构造“形似”函数,稍作变形再构造,对原不等式同解变形,根据相似结构构造辅助函数.