河南省商丘市第一高级中学2023-2024学年第一学期期中考试数学(1)_2023年11月_0211月合集_2024届河南省商丘市第一高级中学第一学期期中考试

河南省商丘市第一高级中学 2023-2024 学年第一学期期中考试
高三数学试卷
一、单选题：（本题共 8小题，每题 5分，共40分）
1．若i是虚数单位，则复数z i2019 23i 的虚部等于（ ）
A．2 B．2 C．2i D．2i
2．设集合A  x yln  x3  ，B   x x1  ，则  x 1 x3  （ ）
A．ð  AB  B．ð  AB  C．A ð B  D．A ð B 
R R R R
x2 2
3．函数 y sinxln 的图象可能是（ ）．
x2
A． B．
C． D．
1
4．已知命题“xR，使2x2  a1  x 0”是假命题，则实数a的取值范围是（ ）
2
       
A． a a1 B． a 1a3 C． a 1a3 D． a 3a1
5．2020年12月17日凌晨，嫦娥五号返回器携带月球样品在内蒙古四子王旗预定区域安全着陆．嫦娥五号返
回舱之所以能达到如此高的再入精度，主要是因为它采用弹跳式返回弹道，实现了减速和再入阶段弹道调整，
这与“打水漂”原理类似（如图所示）．现将石片扔向水面，假设石片第一次接触水面的速率为100m/s，这是
第一次“打水漂”，然后石片在水面上多次“打水漂”，每次“打水漂”的速率为上一次的90%，若要使石片
的速率低于60m/s，则至少需要“打水漂”的次数为（参考数据：取ln0.60.511，ln0.90.105）（ ）A．4 B．5 C．6 D．7
22 2
6．若 a 为等差数列，S 是其前n项的和，且S  ， b 为等比数列，b b  ，则tan  a b 
n n 11 3 n 5 7 4 6 6
的值为（ ）
3 3
A． 3 B． 3 C． D．
3 3
     
7．设非零向量a,b的夹角为θ，定义运算a*b a b sin．下列叙述错误的是（ ）
   
A．若a*b 0，则a//b
       
 
B．a* bc a*ba*c （c为任意非零向量）
     
C．设在△ABC中，AB a，AC b，则2S a*b
△ABC
   
 
D．若 a  b 1，则 a*b 1
max
8．已知函数 f  x 2xxlnx的图象上有且仅有两个不同的点关于直线 y 1的对称点在kx y10的图
象上，则实数k的取值范围是（ ）
A．,1  B． 0, C．
0,1
 D．,1 
二、多选题（本题共 4小题，每题 5分，部分选对得 2分，共 20分）
9．已知数列 a 满足a 2a 2n1a n2n1，则（ ）
n 1 2 n
A．a 2n2 B． a 的前n项和为n  n3 
n n
 
C． 1 n a 的前100项和为100 D．  a 10  的前20项和为284
n n
4ex
10．已知函数 f  x  ，则（ ）
ex 1
A． f  sinx 是周期函数 B．函数 f  x 在定义域上是单调递增函数
C．函数 y  f  x 2是偶函数 D．函数 f  x 的图象关于点 0,2 对称
  1  1 
11．已知向量m 2, ，n  ,4，其中a0,b0，则下列说法正确的是（ ）
 a b 
 
A．若m,n，可以作为平面向量的一组基底，则log ab3
2
 
B．若mn，则22ab 1 
C．若ab1，则m,n有最小值64 2
  b  7 
D．若 m  n 4 2，则 1, 
 
a 2
 
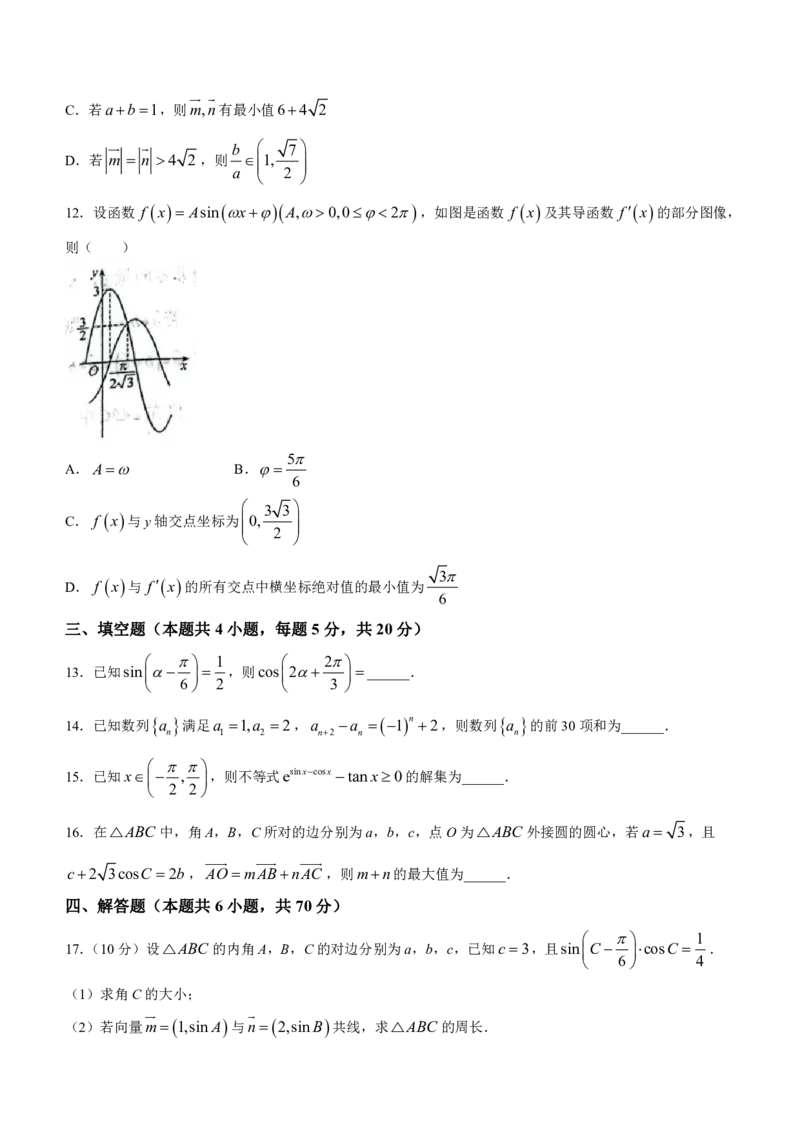
12．设函数 f  x  Asin x A,0,02，如图是函数 f  x 及其导函数 f x 的部分图像，
则（ ）
5
A．A B．
6
 3 3
C． f  x 与y轴交点坐标为0, 
 
2
 
3
D． f  x 与 f x 的所有交点中横坐标绝对值的最小值为
6
三、填空题（本题共 4小题，每题 5分，共20分）
  1  2
13．已知sin    ，则cos2  ______．
 6 2  3 
14．已知数列 a 满足a 1,a 2，a a 1 n 2，则数列 a 的前30项和为______．
n 1 2 n2 n n
  
15．已知x   , ，则不等式esinxcosx tanx0的解集为______．
 2 2 
16．在△ABC中，角A，B，C所对的边分别为a，b，c，点O为△ABC外接圆的圆心，若a  3，且
  
c2 3cosC 2b，AO mABnAC ，则mn的最大值为______．
四、解答题（本题共 6小题，共 70分）
  1
17．（10分）设△ABC的内角A，B，C的对边分别为a，b，c，已知c3，且sinC  cosC  ．
 6 4
（1）求角C的大小；
 
（2）若向量m
1,sinA
与n
2,sinB
共线，求△ABC的周长．1
18．（12分）已知函数 f  x log  1x alog  1x  aR ，且满足 f   1log 4．
3 3 2 3
（1）求函数 f  x 的定义域及a的值；
（2）若关于x的方程x3fx t 0  tR 有两个不同的实数解，求t的取值范围．
19．（12分）已知数列 a 中，a 2，na  n1  a 2  n2 n  nN 
n 1 n1 n 
a 
（1）证明：数列 n是等差数列，并求数列 a 的通项公式；
 n  n
2n1 n
（2）设b  ，数列 b 的前n项和为T ，若T   nN 恒成立，试求实数λ的取值范围．
n a a n n n n1 
n n1
    
20．（12分）已知向量a  sinx,1 ，b  3cosx,2  ，函数 f  x   ab  a．
 
（1）若a//b，求cos2x的值；
1
（2）已知△ABC为锐角三角形，a，b，c为△ABC的内角A，B，C的对边，b2，且 f  A  ，求△ABC
2
面积的取值范围．
 4
21．（12分）已知函数 f  x 定义在区间1,1 内， f     2，且当x,y1,1 时，恒有
 5
 x y 
f  x  f  y  f  ．
1xy
（1）证明： f  x 为奇函数；
1 2a 2 3 n1
（2）若数列 a  ,  b 满足0a 1，a  ，a  n ，b    ，且对
n n n 1 2 n1 a2 1 n f  a  f  a  f  a 
n 1 2 n
nN*，1 n b 6 4，求λ的取值范围．
n
2
22．（12分）已知函数 f  x lnxax ．
ax
（1）若 f  x 0，求实数a的取值范围；
2
（2）若g  x  f  x x2 有两个极值点分别为x ,x  x  x ，求2g  x g  x 的最小值．
ax 1 2 1 2 1 2