数学试卷_2024-2025高二（7-7月题库）_2025年6月试卷_0606浙江省北斗星盟2024-2025学年高二下学期阶段性联考_浙江省北斗星盟2024-2025学年高二下学期阶段性联考数学试卷（PDF版，含答案）

2024 学年第二学期浙江北斗星盟阶段性联考 高二年级数学试题 命题学校：余杭高级中学 东阳中学 审题学校：严州中学 考生须知： 1．本卷共4 页满分150分，考试时间120分钟； 2．答题前，在答题卷指定区域填写班级、学号和姓名；考场号、座位号写在指定位置； 3．所有答案必须写在答题纸上，写在试卷上无效； 4．考试结束后，只需上交答题纸。 一、单选题：本题共8小题，每小题5分，共40分. 在每小题给出的四个选项中，只有一项 是符合题目要求的. 1.设i为虚数单位，若复数z  a25a6  (a2)i是纯虚数，则实数a的值为（ ） A. 2 B. 3 C. 5 D. 2或3 2.定义集合A、B的“对称差集”：A△B={x|x∈A∪B且x∉ A∩B}.已知集合A={1,2,3}， B={2,3,4}，C={4,5}，下列结论正确的是（ ） A.A△B={1,4} B.A△ = C.(A△B)△C≠A△(B△C) D.若 A△B=A，则B≠ 3.命题p：函数 f(x)sin(2∅x∅) 的图象关于直线 x 对称；命题q：  5 2k,k∅ Z. 3 6 则p是q的（ ） A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 4.已知m，n为空间中不重合的直线，、、为不重合的平面，下列命题正确的是（ ） A．若m//,n，则m//n B．若//,m，则m// C．若，，则// D．若a，b，a//b，则// 5.已知F，F 是双曲线 的两个焦点， 为 上一点，且F PF 30，|PF | 3|PF |， 1 2 1 2 1 2 则 的离心率为（ ） 3 1 1 3 A.1 3 B.1 C.  3 D. 2 2 2 6.在空间四边形ABCD中，M、N分别是AB、CD的中点，且AB⊥AD，CB⊥CD.设 ABa, ACb,ADc ，则下列结论正确的是（ ） 1 1 2 2 A. MN  (acb) B. MN  (bac) C. c(ba)c D. b(ca)b 2 2 高二数学学科 试题 第1页(共4页)7.杭州“六小龙”企业(宇树科技、深度求索、游戏科学、群核科技、强脑科技、云深处科技)在 科技领域大放异彩。现从这6家企业中选出4家，分别派往A、B、C、D四个不同的科技交流活动 进行成果展示，且必须同时满足条件:①宇树科技和深度求索中至少有一家被选中；②若宇树科技被 选中，则必须去A活动，若深度求索被选中，则不能去D活动.则不同的安排方式种数是（ ）​ A.96​ B.120​ C.240 ​ D.336 8.已知连续型随机变量服从正态分布N(1,4)，记函数 f(x) P( x)，则 f (x)的图象（ ） A. 关于直线x 1对称 B. 关于直线x 2对称 1 1 C. 关于点(1, )成中心对称 D. 关于点(2, )成中心对称 2 2 二、多选题：本题共3小题，每小题6分，共18分. 在每小题给出的选项中，有多项符合题目要求. 全部选对的得满分，部分选对的得部分分. 9.已知数列a 2n1的前n项和为S ，数列b 2a n 1的前n项和为T ，则下列说法正确的是（ ） n n n n A．S S S B．3(S S )S C．T T T2 D．T2 T2 T (T T ) 2 4 6 4 2 6 2 6 4 2 4 2 4 6 10.已知P(x ,y ),P(x ,y )是曲线C:xy(xy1)2上的两个动点，则( ) 1 1 1 2 2 2 A.曲线C是中心对称图形 B.曲线C有且只有两条渐近线 C.若P,P 分别在第二象限和第四象限，则|PP |的最小值为2 1 2 1 2 D.曲线C和圆E：x2y2 4恰好有6个公共点 11.甲､乙两人进行象棋比赛，赛前每人发3枚筹码.一局后负的一方，需将自己的一枚筹码给对方； 若平局，双方的筹码不动，当一方无筹码时，比赛结束，另一方最终获胜.由以往两人的比赛结果可 知，在一局中甲胜的概率为0.3，乙胜的概率为0.2.用P(i0,1,,6)表示“在甲所得筹码为i枚时， i 最终甲获胜的概率”，则( ) A.第一局比赛后甲的筹码个数记为X ，则期望E(X)3.1 B.四局比赛后，比赛结束的概率为0.0405 C.P P 1 0 6 2 D.P P  (P P ) 6 1 3 5 0 三、填空题：本题共3小题，每小题5分，共15分.  12.若3sin( )sin 10 ，则tan=_________． 2 13.(x2 2x3)4的展开式中x3的系数为 ． 14.已知不等式ex cosxax2 ax 0对任意实数x都成立，则实数a的值为 ． 高二数学学科 试题 第2页(共4页)四、解答题：本题共5小题，共77分. 解答应写出文字说明、证明过程或演算步骤. 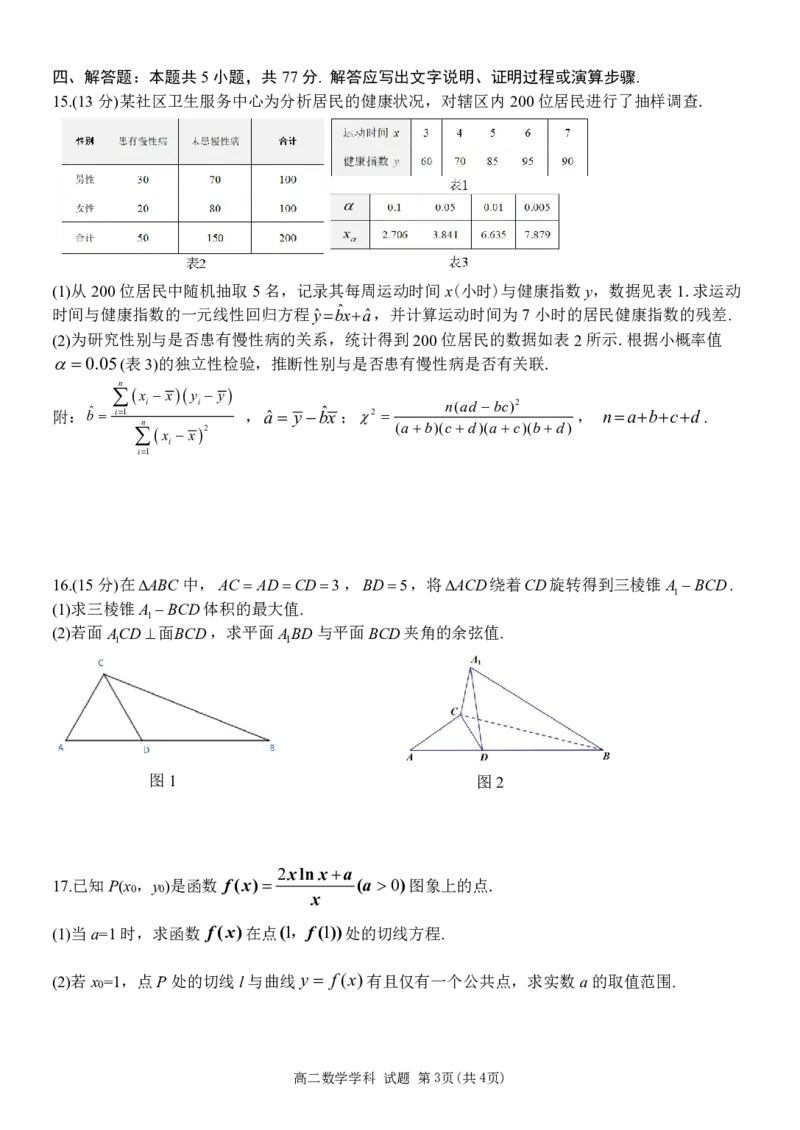15.(13分)某社区卫生服务中心为分析居民的健康状况，对辖区内200位居民进行了抽样调查. (1)从200位居民中随机抽取5名，记录其每周运动时间x(小时)与健康指数y，数据见表1.求运动 时间与健康指数的一元线性回归方程yˆb ˆ xaˆ，并计算运动时间为7小时的居民健康指数的残差. (2)为研究性别与是否患有慢性病的关系，统计得到200位居民的数据如表2所示.根据小概率值 0.05(表3)的独立性检验，推断性别与是否患有慢性病是否有关联. n x xy  y 附：bˆ i1 i i ，aˆ  yb ˆ x；2  n(ad bc)2 ， nabcd.  n x x2 (ab)(cd)(ac)(bd) i i1 16.(15分)在ABC 中，AC ADCD3，BD5，将ACD绕着CD旋转得到三棱锥A BCD. 1 (1)求三棱锥A BCD体积的最大值. 1 (2)若面ACD面BCD，求平面ABD与平面BCD夹角的余弦值. 1 1 图1 图2 2xlnxa 17.已知P(x ，y )是函数 f(x) (a 0)图象上的点. 0 0 x (1)当a=1时，求函数 f(x)在点(1，f(1))处的切线方程. (2)若x =1，点P处的切线l与曲线 y  f(x)有且仅有一个公共点，求实数a的取值范围. 0 高二数学学科 试题 第3页(共4页)3 18.设A,B两点的坐标分别为2,0,2,0，直线AP,BP相交于点P，且它们的斜率之积为 ， 4 设点P的轨迹为曲线E． (1)求曲线E的标准方程； (2)若直线l过点Q1,0，与曲线E交于C,D两点，C在x轴上方，直线AC,BD交于点M ，直线 AD,BC 交于点N ．记A,B到直线l的距离分别为d ,d ． 1 2 9 1 （ⅰ）证明：  4． （ⅰⅰ）求AMN的面积最小值． d d 1 2 a a  a   11 12 1n 19.已知n行n列(n2)的数表 A a 21 a 22  a 2n 中，对任意的i{1,2,,n}， j{1,2,,n}，都有          a a  a  n1 n2 nn n n n n a {0,1}.若当a  0时，总有a a  n，则称数表A为典型表，此时记S  a . ij st it sj n ij i1 j1 i1 j1 1 1 0 0 0 0 1   (1)若数表 B  1 0 0  ， C 1 1 0 0，请判断B，C 是否为典型表，并说明理由；     0 0 1 1 1 1 0     0 0 1 1 (2)当n6时，是否存在典型表A使得S 17，若存在，请写出一个A；若不存在，请说明理由； 6 2n (3)记S 的最小值为Sn ，求[(1)iSi ]. n min min i1 高二数学学科 试题 第4页(共4页)