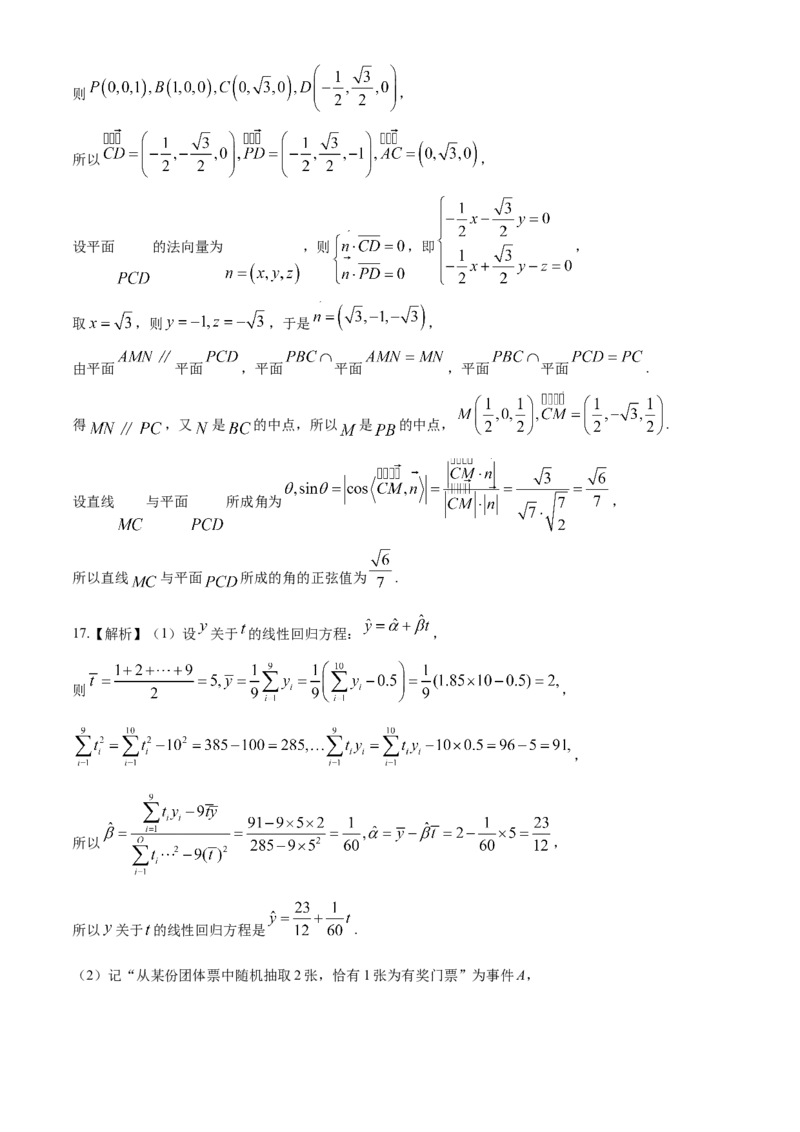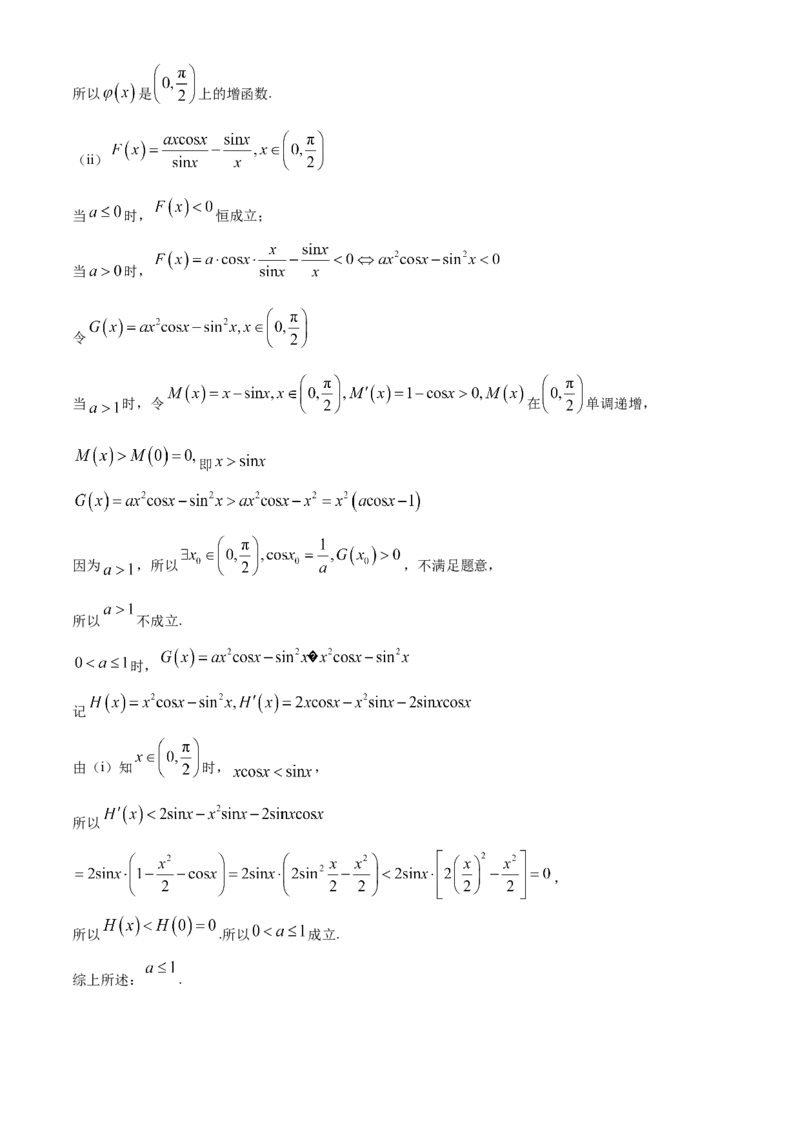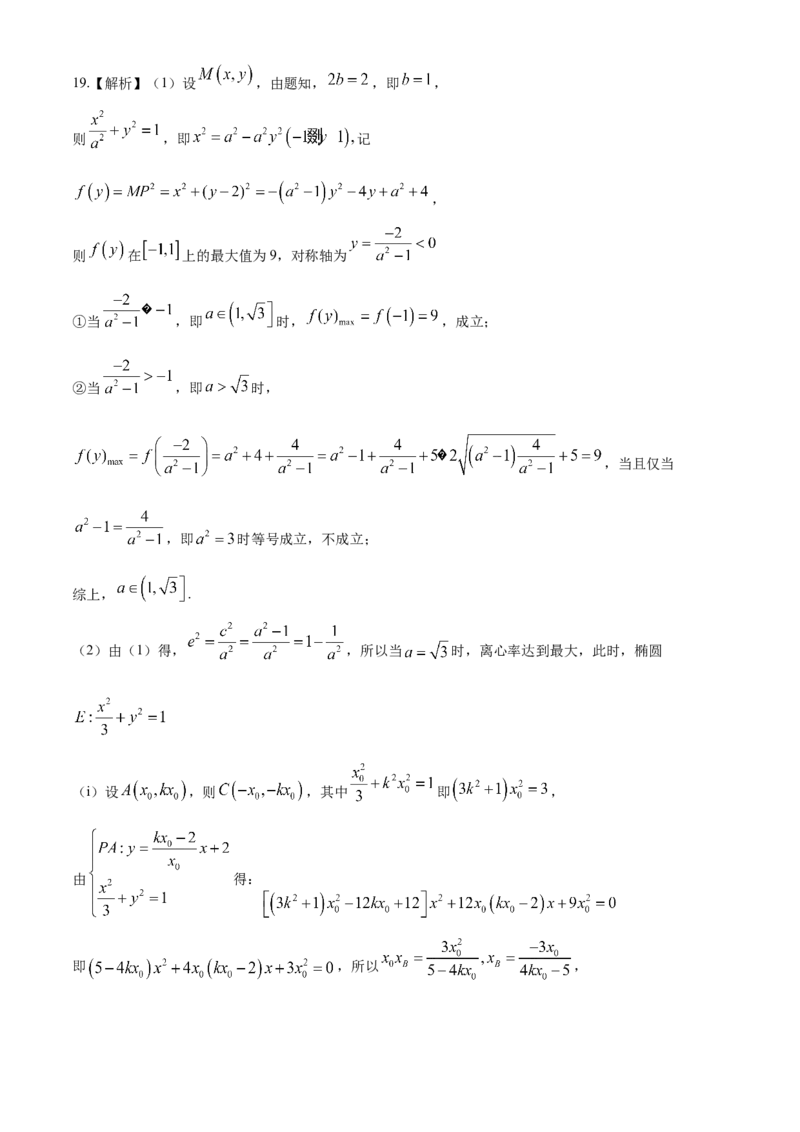文档内容
数学
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
1.已知集合 ,则“ ”是“ ”的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
2.若复数 满足 ,则 等于( )
A. B. C. D.2
3.圆 被直线 所截线段的长度为( )
A.2 B.4 C. D.
4.某外来入侵植物生长迅速,繁殖能力强,大量繁殖会排挤本地植物,容易形成单一优势种群,导致原有
植物种群的衰退甚至消失,使当地生态系统的物种多样性下降,从而破坏生态平衡.假如不加控制,它的总
数量每经过一年就增长一倍.则该外来入侵植物由入侵的1株变成100万株大约需要( )(参考数据:
)
A.40年 B.30年 C.20年 D.10年
5.已知某圆锥底面半径为1,高为2,则该圆锥的外接球表面积为( )
A. B. C. D.
6.在二项式 的展开式中,记各项的系数和为 ,则 被5除所得的余数是( )
A.4 B.3 C.2 D.1
7.在 中, 为线段 的中点,过 的直线分别与线段 交于 ,且
,则 ( )
A. B. C. D.
8.将一颗骰子连续抛掷三次,向上的点数依次为 ,则 的概率为( )A. B. C. D.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有错的得0分.
9.已知函数 ,则( )
A. 最小正周期为
B. 是 图象的一条对称轴
C. 是 图象的一个对称中心
D. 在 上单调
10.已知正实数 满足 ( 是自然对数的底数, ),则( )
A. B.
C. 的最大值为 D.方程 无实数解
11.如图,一个棱长为6的透明的正方体容器(记为正方体 )放置在水平面 的上方,
点 恰在平面 内,点 到平面 的距离为2,若容器中装有水,静止时水面与表面 的交线与
的夹角为0,记水面到平面 的距离为 ,则( )
A.平面 平面
B.点 到平面 的距离为8
C.当 时,水面的形状是四边形D.当 时,所装的水的体积为
三、填空题:本大题共3小题,每小题5分,共15分.
12.在 中,内角 的对边分别是 .若 ,则 __________.
13.已知双曲线 的左、右焦点分别是 ,若双曲线左支上存在点 ,使得
,则该双曲线离心率的最大值为__________.
14.对于有穷数列 ,从数列 中选取第 项、第 项、 、第 项 ,顺次排列构成数
列 ,其中 ,则称新数列 为 的一个子列,称 各项之和为 的一个子
列和.规定:数列 的任意一项都是 的子列.则数列 的所有子列和的和为__________.
四、解答题:本大题共5小题,计77分.解答应写出必要的文字说明、证明过程或演算步骤.
15.(本小题满分13分)
已知各项均为正数的数列 前 项和为 ,且 .
(1)求数列 的通项公式;
(2)证明: .
16.(本小题满分15分)
如图,在四棱锥 中,底面 是等腰梯形, ,点 在 上,
点 在 上,平面 平面 .
(1)求证: 是 的中点;(2)若 ,求直线 与平面 所成角的正弦值.
17.(本小题满分15分)
扬州是国家历史文化名城,“烟花三月下扬州”“春风十里扬州路”传诵千年.为了给来扬州的客人提供最
好的旅游服务,某景点推出了预订优惠活动,下表是该景点在某App平台10天预订票销售情况:
日期 1 2 3 4 5 6 7 8 9 10
销售量 (万
1.93 1.95 1.97 1.98 2.01 2.02 2.02 2.05 2.07 0.5
张)
经计算可得: .
(1)因为该景点今年预订票购买火爆程度远超预期,该App平台在第10天时系统异常,现剔除第10天数
据,求 关于 的线性回归方程(结果中的数值用分数表示);
(2)该景点推出团体票,每份团体票包含四张门票,其中 张为有奖门票(可凭票兑换景点纪念品),
的分布列如下:
2 3 4
今从某份团体票中随机抽取2张,恰有1张为有奖门票,求该份团体票中共有3张有奖门票的概率.
附:对于一组数据 ,其回归线 的斜率和截距的最小二乘估计分别
为:
18.(本小题满分17分)
已知函数 .
(1)求函数 的极值;
(2)函数 .
(i)讨论函数 的单调性;
(ii)函数 ,求实数 的取值范围.
19.(本小题满分17分)己知椭圆 短轴长为2,椭圆 上一点 到 距离的最大值为3.
(1)求 的取值范围;
(2)当椭圆 的离心率达到最大时,过原点 斜率为 的直线 与 交于 两点, 分
别与椭圆 的另一个交点为 .
(i)是否存在实数 ,使得 的斜率 等于 ?若存在,求出 的值;若不存在,说明理由;
(ii)记 与 交于点 ,求线段 长度的取值范围.
扬州市 2024 届高三考前调研测试
数学参考答案
1.B 2.A 3.D 4.C 5.C 6.D 7.B 8.D
9.BC 10.ACD 11.ABD
12. 13.3 14.2016
15.【解析】(1)因为 ①,所以 ②, ③,
由③得: ,所以 ,
②-①得: ,整理得: ,又因为 各项均为正数,所以 ,
所以 是公差 的等差数列, .
(2)证明:由(1), ,
所以 ,
所以 .
16.【解析】
(1)因为平面 平面 ,平面 平面 ,
平面 平面 .所以 ,
又由梯形 可得 ,所以四边形 为平行四边形,
所以 ,所以 是 的中点.
(2)连接 ,由(1)知 是 的中点, ,所以 ,即 ,
因为 ,所以 与 全等,
所以 ,即 ,
又 平面 ,所以 平面 ,
以 为正交基底,建立如图所示空间直角坐标系 ,则 ,
所以 ,
设平面 的法向量为 ,则 ,即 ,
取 ,则 ,于是 ,
由平面 平面 ,平面 平面 ,平面 平面 .
得 ,又 是 的中点,所以 是 的中点, .
设直线 与平面 所成角为 ,
所以直线 与平面 所成的角的正弦值为 .
17.【解析】(1)设 关于 的线性回归方程: ,
则 ,
,
所以 ,
所以 关于 的线性回归方程是 .
(2)记“从某份团体票中随机抽取2张,恰有1张为有奖门票”为事件A,“该份团体票中共有 张有奖门票”为事件 ,则 ,
,所以 ,
,所以
.
所以 .
答:所求概率是 .
18.【解析】(1)函数 ,导函数 ,
令 或
+ 0 - 0 +
极大 极小
由上表,函数 极大值为 ,极小值为
(2)(i)
记 ,
则
时, ,所以 时, ,所以 ,所以 是 上的增函数.
(ii)
当 时, 恒成立;
当 时,
令
当 时,令 在 单调递增,
即
因为 ,所以 ,不满足题意,
所以 不成立.
时,
记
由(i)知 时, ,
所以
,
所以 .所以 成立.
综上所述: .19.【解析】(1)设 ,由题知, ,即 ,
则 ,即 记
,
则 在 上的最大值为9,对称轴为
①当 ,即 时, ,成立;
②当 ,即 时,
,当且仅当
,即 时等号成立,不成立;
综上, .
(2)由(1)得, ,所以当 时,离心率达到最大,此时,椭圆
(i)设 ,则 ,其中 即 ,
由 得:
即 ,所以 ,所以 ,同理可得:
所以, 的斜率
(ii)由(i)知,
由 ., ,即 ,将 代入椭圆方程得: ,
所以, 的轨迹方程为 ,
所以,线段 长度的取值范围为 .