江西省重点中学协作体2024届高三第一次联考数学参考答案24.2.2(2)_2024年2月_01每日更新_24号_2024届江西省重点中学协作体高三下学期第一次联考

二、多选题：本大题共3小题，每小题6分，共18分. 江西省重点中学协作体 2024 届高三第一次联考数学参考答案 题号 9 10 11 一、单选题：本大题共8小题，每小题5分，共40分. 答案 AD BCD ABD 题号 1 2 3 4 5 6 7 8 1 9.【答案】AD【详解】对于A，一个总体含有50个个体，某个个体被抽到的概率为 ， 答案 B C D A C B D C 50 以简单随机抽样方式从该总体中抽取一个容量为10的样本， 1.【答案】B；2.【答案】C；3.【答案】D 1 1 则指定的某个个体被抽到的概率为 10 0.2 ，故A正确； 1 3 3 π 3 50 5 4.【答案】A由2sin32 3cos，得 sin cos ，即sin( ) ， 2 2 4 3 4 对于B，Q数据1，2，m，6，7的平均数是4，m4512674， π π π π π 3 1 所以sin(2 6 )sin[2( 3 ) 2 ]cos2( 3 )12sin2( 3 )12( 4 )2  8 . 这组数据的方差是s2  1 5   142242442642742   2 5 6 ，故B错误； 5.【答案】C；6.【答案】B 1719 7.【答案】D【详解】丙队在输了第一场的情况下，其积分仍超过其余三支球队的积分，三队中选一队 对于C，8个数据50百分为850%4，第50百分位数为 =18，故C错误； 2 1 与丙比赛，丙输，C1 ，例如是丙甲， 3 3 对于D，依题意，Dx82，则D2x122Dx162， 若丙与乙、丁的两场比赛一赢一平，则丙只得4分，这时，甲乙、甲丁两场比赛中甲只能输，否则甲 的分数不小于4分，不合题意，在甲输的情况下，乙、丁已有3分，那个它们之间的比赛无论什么情 所以数据2x 1,2x 1,,2x 1的标准差为16，D正确. 况， 乙、丁中有一人得分不小于4分，不合题意. 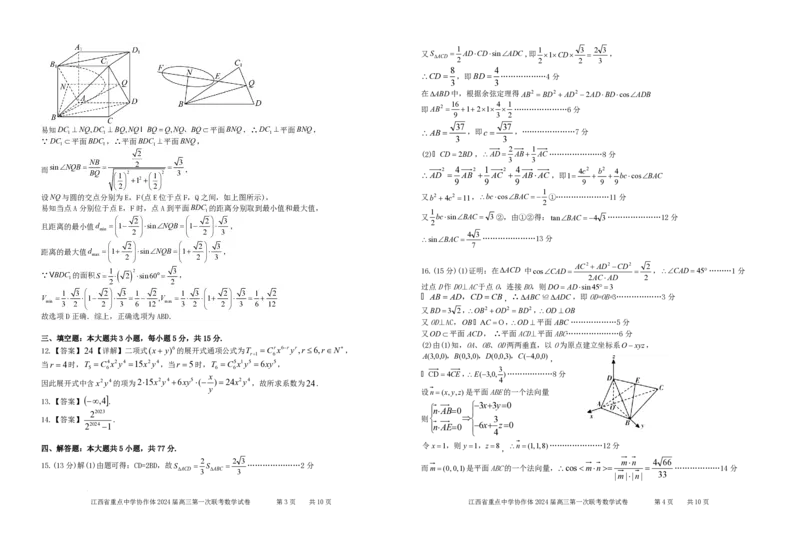1 2 10 1 10.【答案】BCD 若丙全赢（概率是( )2）时，丙得6分，其他3人分数最高为5分，这时甲乙，甲丁两场比赛中甲不 3 11.【答案】ABD【详解】对于A项，如图所示，连接对应面对角线， 1 根据正方体的性质可知：BD//BD ， 能赢，否则甲的分数不小于6分，只有平或输，一平一输，概率是C1( )2，如平乙，输丁，则乙丁比 1 1 2 3 BD平面BDA，BD 平面BDA， 1 1 1 1 1 1 2 ∴BD//平面BDA，同理可知CD//平面BDA， 赛时，丁不能赢，概率是 ， 1 1 1 1 1 3 又BDI DC,BD、DC 平面BCD， 1 1 1 1 两场均平，概率是( )2，乙丁这场比赛无论结论如何均符合题意， ∴平面BCD//平面BDA， 1 1 1 3 又PCD，∴BP平面BCD， 1 1 1 1 两场甲都输，概率是( )2，乙丁这场比赛只能平，概率是 . ∴BP//平面BDA，故A正确; 1 1 3 3 对于B项，易知BB 面ABCD ， 1 1 1 2 1 1 1 8 1 1 1 1 1 综上，概率为C1 ( )2[C1 ( )2 ( )2 ( )2 ] ，D正确． AC 面ABCD ，则AC BB， 3 3 3 2 3 3 3 3 3 35 1 1 1 1 1 1 1 1 1 又AC BD,BD I BB B,BD、BB 平面BBD， 8.【答案】C【详解】因为g3x为偶函数，gx fx1，所以 fx4 fx4， 1 1 1 1 1 1 1 1 1 1 1 1 ∴AC 平面BBD，而BD 平面BBD， 对 f(2x) f(2x)4x两边同时求导，得 f(2x) f(2x)4，所以有 1 1 1 1 1 ∴BD  AC ，同理BD DC ， f(4x) f(x)4 f(4x) f(x)4 f(4x) f(x)4 f(8x) f(x), 1 1 1 1 1 所以函数 fx的周期为8，在 f(2x) f(2x)4中，令x0，所以 f(2)2， 又DC 1 I A 1 C 1 C 1 ,DC 1 、A 1 C 1 平面A 1 C 1 D， ∴BD 平面ACD， 因此g17 f18 f22，因为g3x为偶函数， 1 1 1 又∵BD 平面PBD ，∴平面PBD 平面ACD，故B正确; 所以有g3xg3xg3xg3xg7g11， 1 1 1 1 1 对于C项，因为BM 为定直线，DBM 是定角，D 到BM 的距离为定值， 1 1 f(8x) f(x)g7xgx1g7xgx1g7g12， 所以MBPMBD 时，P在以BM 为旋转轴，D 到BM 的距离为半径的圆锥上， 1 1 由1,2可得：g70，所以g7g172. 又BM //平面CDDC ，故平面CDDC 截圆锥的轨迹为双曲线的一支，即C错误； 1 1 1 1 对于D项，设AB,DC 中点分别为N，Q， 1 1 2 则点A的运动轨迹是平面ABCD内以N为圆心， 为半径的圆(如图)， 1 1 2 江西省重点中学协作体2024届高三第一次联考数学试卷 第1页 共10页 江西省重点中学协作体2024届高三第一次联考数学试卷 第2页 共10页 学科网（北京）股份有限公司1 1 3 2 3 又S  ADCDsinADC,即 1CD  ， ACD 2 2 2 3 8 4 CD  ，即BD ………………4分 3 3 在ABD中，根据余弦定理得AB2 BD2  AD2 2ADBDcosADB 16 4 1 即AB2  121  …………………6分 9 3 2 易知DC 1 NQ,DC 1 BQ,NQI BQQ,NQ、BQ平面BNQ，∴DC 1 平面BNQ， AB 37 ，即c 37 ，…………………7分 ∵DC 平面BDC ，∴平面BDC 平面BNQ， 3 3 1 1 1 2 1 2 (2) CD2BD，AD AB AC…………………8分 3 3 NB 2 3 而 sinNQB BQ  1 2 1 2  3 ， AD 2  4 AB 2  1 AC 2  4 ABAC，即1 4c2  b2  4 bccosBAC   12  9 9 9 9 9 9 2 2 1 设NQ与圆的交点分别为E，F(点E位于点F，Q之间，如上图所示)， 又b2 4c2 11，bccosBAC ①…………………11分 2 易知当点A分别位于点E，F时，点A到平面BDC 的距离分别取到最小值和最大值， 1 1  2  2 3 又 2 bcsinBAC 3②，由①②得：tanBAC4 3…………………12分 且距离的最小值d 1 sinNQB1  ， min  2   2  3     4 3 sinBAC …………………13分  2  2 3 7 距离的最大值d 1 sinNQB1  ， max  2   2  3     AC2AD2CD2 2 ∵VBDC 1 的面积S  1   2 2 sin60o 3 ， 16.(15分)(1)证明：在ACD 中cosCAD 2ACAD  2 ，CAD45………1分 2 2 过点D作DO⊥AC于点O，连接BO，则DO ADsin453 1 3  2 3 1 2 1 3  2 3 1 2 V   1    ,V   1     AB AD，CD CB ，∴ABC≌ADC，即OD=OB=3………………3分 min 3 2  2  3 6 12 max 3 2  2  3 6 12     又BD3 2，OB2 OD2 BD2，ODOB 故选项D正确．综上，正确选项为ABD． 又OD⊥AC，OB AC O，OD平面 ABC ………………5分 又OD平面 ACD， ∴平面ACD⊥平面ABC…………………6分 三、填空题：本大题共3小题，每小题5分，共15分. (2)由(1)知，OA、OB、OD两两垂直，以O为原点建立坐标系Oxyz， 12.【答案】24【详解】二项式(x y)6的展开式通项公式为T Crx6ryr,r 6,rN， r1 6 A(3,0,0)，B(0,3,0)，D(0,0,3)，C(4,0,0) ， 当r 4时，T C4x2y4 15x2y4，当r 5时，T C5x1y5 6xy5， 5 6 6 6 3 x  CD4CE，E(3,0, )………………8分 因此展开式中含x2y4的项为215x2y4 6xy5( )24x2y4 ，故所求系数为24. 4 y 设n(x,y,z)是平面ABE的一个法向量   13.【答案】 ,4 . 3x3y0 22023  nAB0  14.【答案】 . 则  3 22024 1   nAE0  6x z0  4 四、解答题：本大题共5小题，共77分. 令x1，则y1，z8 ， n(1,1,8)…………………12分 2 2 3 mn 4 66 15.(13分)解(1)由题可得：CD=2BD，故S ACD  3 S ABC  3 …………………2分 而m(0,0,1)是平面ABC的一个法向量，cosmn  ………………14分 |m||n| 33 江西省重点中学协作体2024届高三第一次联考数学试卷 第3页 共10页 江西省重点中学协作体2024届高三第一次联考数学试卷 第4页 共10页 学科网（北京）股份有限公司2 3y 4 60y 2 225 3 3 设二面角EABC平面角的大小为，则tan 整理得x M M  ，此时直线CD经过定点( ,0)……………14分 8 2y 4 40y 2 150 2 2 M M 2 二面角EABC的正切值为 ………………15分 3 8 综上，直线CD经过定点( ,0)………………15分 2 另解：(ii)当直线CD不垂直于x轴时，由对称性知定点在x轴上，设Q(t,0) 30y 10y 17.(15分)解(1)设C(x ,y )，由题可知，k k k k ………………2分 M M 1 1 AC BC AM BN 45 y 2 5 y 2 又k AM k BN  y M 27 y N ，由k AC k BC  x 1 y  1 3  x 1 y  1 3  x 1 y 2 1  2 9 …………………4分 由C、D、Q三点共线知 3y M 2 1 M 35 t  3y M 2  M 15 t 45 y 2 5 y 2 x 2 y 2 5 M M  点C(x y )在E上， 1  1 1，k k  ………………… 5分 1 1 9 5 AC BC 9 化简得： 64t  y 2 9060t 0，则t  3 y y 15………………6分 M 2 M N y 3 （2)由题可知，直线MA的方程为：y M (x3) 此时直线CD经过定点( ,0)……………14分 9 2  y 3 y  M (x3) 综上，直线CD经过定点( ,0)………………15分 联立方程 9 可得：(45 y 2)x2 6y 2x9y 2 4050 2 M M M  5x2 9y2 45 解法二： (1)设C(x ,y )，则AC (x 3，y )，AM (9,y )， 36y 2 4(45 y 2)(9y 2 405)=45>0………………7分 1 1 1 1 M M M M 9y  3x  9y M 2 405 ， x  3y M 2 135 ………………8分 ∵A、C、M三点共线，∴y M  x  1 3 ，…………………2分 1 45 y 2 1 45 y 2 1 M M 3y 27y2 又y  y M (x 3)，y  30y M ，C（ 3y M 2 135 , 30y M ） 同理：y N  x 1  1 3 ，∴y M y N  x 1 2  1 9 …………………4分 1 9 1 1 45y M 2 45 y M 2 45 y M 2 又点C(x ,y )在曲线E上，∴ x 1 2  y 1 2 1，代入上式得：y y 15………………6分 1 1 M N 3y 2 15 10y 9 5 同理可得点D的坐标为（ M , M ）………………9分 y y 5 y 2 5 y 2 (2)由k  M ，k  M 得k 3k M M AC 9 BM 3 BM AC 3y 2 135 3y 2 15 (i)当直线CD垂直于x轴时，x C x D ，即 45 M  y 2  5 M  y 2 ,y M 2 15 又k AC k BC  x y  1 3  x y  1 3  9 5 ，∴k BC k BD 3k BC k AC  5 3 …………………8分 M M 1 1 3 3 由题可得直线CD显然不与x轴平行 x x  ，此时直线CD的方程为x ………………10分 C D 2 2 设直线CD的方程为：xmyn(n3)，C(x ,y )，D(x ,y ) 1 1 2 2 (ii)当直线CD不垂直于x轴时， xmyn  30y 10y 由 得(5m2 9)y2 10mny5n2 450…………………9分 45 y M 2  5 y M 2 20y 3 300y  5x2 9y2 45 k CD  3y 2  M 135 3y M 2 15  3 M y 4 675 M ………………11分  y  y  10mn 45 M  y M 2  5 M  1 y 0 M y 2 20y M 3 300y 3y 2 15 由0得     y 1 y 2  5n2 5m  2 45 9 …………………11分 故直线CD的方程为y M  M M（x M ）………………12分   1 2 5m2 9 5 y 2 3y 4 675 5 y 2 M M M y y y y 又k k  1  2  1 2 1 2y 2 30 3y 2 15 BC BD x 3 x 3 (my n3)(my n3) 令 y=0，则  M （x M ） 1 2 1 2 5 y 2 3y 4 675 5 y 2 y y 5n2 45 M M M  1 2  …………………13分 m2y y mn(y  y )3m(y  y )n2 6n9 9n2 54n81 1 2 1 2 1 2 江西省重点中学协作体2024届高三第一次联考数学试卷 第5页 共10页 江西省重点中学协作体2024届高三第一次联考数学试卷 第6页 共10页 学科网（北京）股份有限公司5n2 45 5 3 19.(17分)解(1)若a 1，则 f x xlnx2x2 1，所以 fxlnx14x， 由  得n 或n3(舍去)…………………14分 9n2 54n81 3 2 所以 f1145，又 f 1213，………………2分 3 3 ∴直线CD：xmy ，∴直线CD经过定点( ,0)…………………15分 所以 f x的图象在x1处的切线方程为y35x1，即5x y20.………………3分 2 2 (2)(i)由题意知 fxlnx14ax. 18.(17分)解(1)若n=2，X的取值为0，1，2，Y的取值为0，1，2，…………………1分 1 令gx fxlnx4ax1，则gx 4a. 1 1 则P（X=0，Y=0）=  ，…………………2分 x 32 9 因为 f x有两个极值点x ，x x  x ，所以gx0有两个不等正实根x ，x x  x . 1 2 1 2 1 2 1 2 1 1 2 P（X=0，Y=1）=C1   ，…………………3分 若a0，gx0，则gx在0,上递增， 2 3 3 9 所以gx在0,上至多有一个零点，不符合题意；………………5分 1 1 1 1 2 P（X=0，Y=2）=  ，P（X=1，Y=0）=C1   ，…………………4分 32 9 2 3 3 9 1 若a 0，令gx0，解得x ， 1 1 2 1 1 4a P（X=1，Y=1）=C1   ，P（X=2，Y=0）=  …………………5分 2 3 3 9 32 9 1 1 所以当0 x 时，gx0，当x 时，gx0， P（X=1，Y=2）=P（X=2，Y=1）=P（X=2，Y=2）=0…………………6分 4a 4a 故（X，Y）的联合分布列为  1   1  所以gx在 0, 上递增，在 , 上递减. （X，Y） 0 1 2  4a 4a  1 2 1 1  1  0 所以x 时，gx取得极大值，即最大值为g   ln4a，………………6分 9 9 9 4a 4a 2 2  1  1 1 9 9 0 所以g   ln4a0，解得0a .………………7分 4a 4 1 2 0 0 1  1  1 4a  1  1 9 当0a 时，g   0，又g    0，所以g   g   0， 4 4a e e 4a e …………………7分 1 1  由零点存在性定理知：存在唯一的x   , ，使得gx 0.………………8分 (2)当kmn时,P(X k,Y m)0，…………………9分 1 e 4a 1  1  1 1 4 n nk nk 1 又g   ln 4a 12lna 1， 故 p P(X k,Y m)P(X k,Y m)CkCm  …………………11分 a2  a2 a2 a k n nk 3n m0 m0 m0 4 2 4 42x 令x2lnx 1，所以x   ， x x x2 x2 Ck nk Ck 1 2 = n Cm  n 2nk Ck( )k( )nk…………………13分 所以当0 x2时，x0，当x  2时，x0， 3n nk 3n n 3 3 m0 所以x在0,2上递增，在2,上递减， n n 1 2 4 所以 kp [kCk( )k( )nk]，…………………15分 所以a2lna 1≤22ln210， k n 3 3 a k0 k0  1   1   1  所以g   0，所以g   g   0， n n a2  4a a2  由二项分布的期望公式可得 kp  .…………………17分 k 3  1 1  k0 由零点存在性定理知：存在唯一的x   , ，使得gx 0.………………10分 2 4a a2  2 江西省重点中学协作体2024届高三第一次联考数学试卷 第7页 共10页 江西省重点中学协作体2024届高三第一次联考数学试卷 第8页 共10页 学科网（北京）股份有限公司1 所以当0a 时，gx0有两个不等正实根x ，x . 4 1 2  1 综上，a的取值范围是 0, .………………11分  4 1 1 1 (ii)证明：由①知0a ，且0 x   x ，所以 1， 4 1 4a 2 4a  1  因为gx在 0, 上为增函数，及g114a 0，所以x 1，…………………12分  4a 1 1 1 又x  ，所以x x  1.………………13分 2 4a 2 1 4a 因为gx 0，gx 0，所以lnx 4ax 10，lnx 4ax 10， 1 2 1 1 2 2 1 x x 所以lnx lnx 4ax x ，所以  1 2 .………………14分 1 2 1 2 4a lnx lnx 1 2 2x1 1 4 x12 令hxlnx 0 x1，所以hx   0， x1 x x12 xx12 x  x  所以hx在0,1上递增，因为x  x ，所以 1 1，所以h 1 h10， 1 2 x x   2 2  x  2 1 1 即ln x 1   x 2  0，所以 x 1 x 2  x 1 x 2 ，………………16分 x x lnx lnx 2 2 1 1 1 2 x 2 1 x x x x 1 所以  1 2  1 2 ，即x x  . 4a lnx lnx 2 1 2 2a 1 2 1 1 1 所以3x x x x 2x x   2 2.………………17分 2 1 1 2 2 1 2a 2a a 江西省重点中学协作体2024届高三第一次联考数学试卷 第9页 共10页 江西省重点中学协作体2024届高三第一次联考数学试卷 第10页 共10页 学科网（北京）股份有限公司