文档内容
兰州一中高三年级诊断考试试卷
高三数学答案
一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.)
题号 1 2 3 4 5 6 7 8
答案 C B D D C A D B
二、多选题(本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符
合题目要求,全部选对得6分,部分选对得部分分,有选错的得0分.
题号 9 10 11
答案 ABC BD AB
三、填空题(本大题共3小题,每小题5分,共15分.)
3
、 ,1 13、36 14、
5
1
四
2
、解−答题(本大题共5小题,共77分.解答应写出必要的文字说明、证明过程或演算步
骤。)
15. ( 本 题 13 分 ) 在 Δ 中 , 角 , , 的 对 边 分 别 为 , , , 且
, Δ ABC. (1)求 ;
2 2 2
(+2) 若−在 边=24上且 ABC =12, ,求 的长.
解析:(1)因为 2+ 2 2 =24, =12,
=2 ABC =2 5
所以 2+ 2 2 =2 = .
− ABC Δ
2+ 2 2 1
所以 − = Δ ,得2 = 即 =2.
2 2
−
=2 2 5
(2)因为 =2,所以 ,解得 = ,
2 + 2 =1 5
±
2 5 5
因为 =2> 0,且 为三角形的内角,所以 = , = ,
5 5
1 1 2 5
又因为 = = 2 5 =12,所以 =6.
ABC 2 2 5
Δ 1 2× ×
因为 2 ,∴ = + .
3 3
1 ��� �� 2 ��� �� 1 ��� � 2 1 2
所以 2 =( + )2 =( )2+( )2+2( | |)( | |) ,
3 3 3 3 3 3
��� �� �� 8 � � 0 � 16 ��� � 164 ��� �� 2 � 4 �� 1 � ��� �� ��� �
所以 2 =4+ + = ,所以 = .
9 3 9 3
��� ��
16.(本题15分)已知函数 是定义在 上的奇函数,且当 时, .
2
>0 =− +2
第 1 页 共 4 页
{#{QQABDYIEogigAIJAARgCQwUaCECQkAEACYgGBEAEsAAAwANABAA=}#}(1)求函数 的解析式;
(2)若函数 在 上有三个零点,求 的取值范围.
解析:(1)令 <0,则 >0,又 是定义在 上的奇函数,
= +
所以可得 = = [ 2+2 ]= 2+2 ,
−
2+2 , 0,
又 0 = 0, 故函−数 − 的解−析式−为− = −
2+2 , <0.
− ⩾
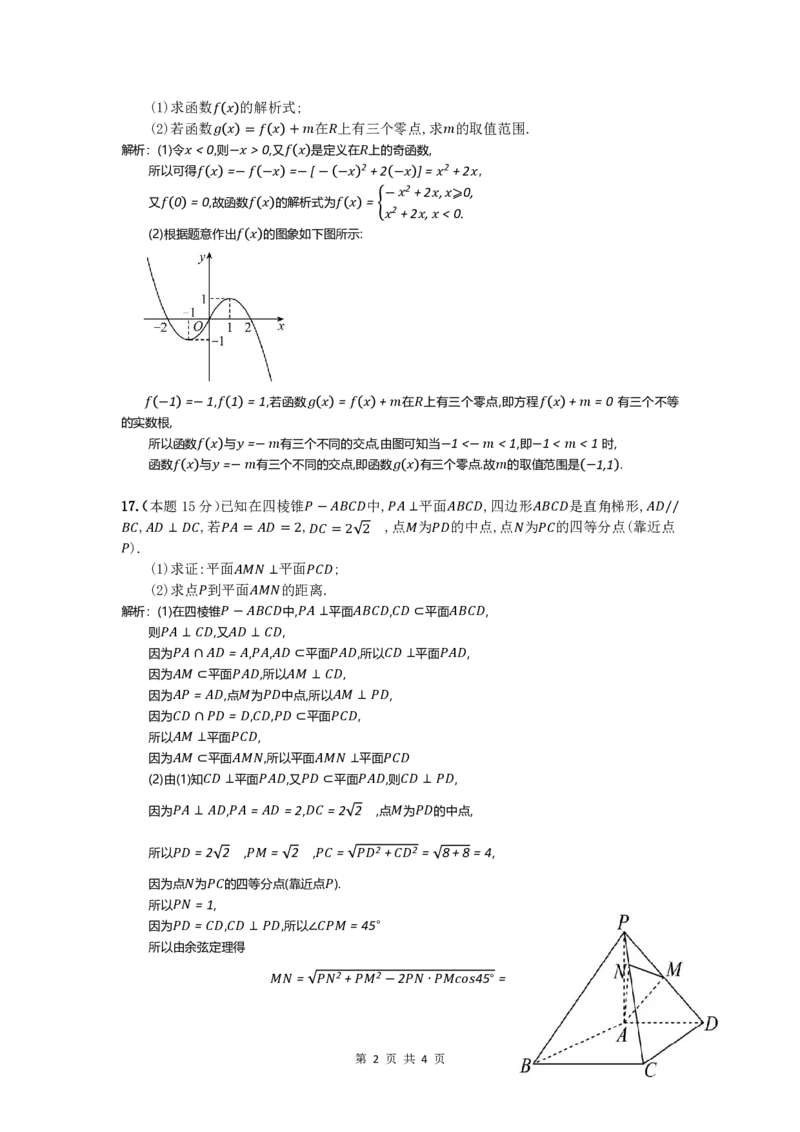
(2) 根据题意作出 的图象如下图 所示 :
1 = 1, 1 =1,若函数 = + 在 上有三个零点,即方程 + =0 有三个不等
的实数根,
− −
所以函数 与 = 有三个不同的交点,由图可知当 1< <1,即 1< <1时,
函数 与 = 有三个不同的交点,即函数 有三个零点.故 的取值范围是 1,1 .
− − − −
− −
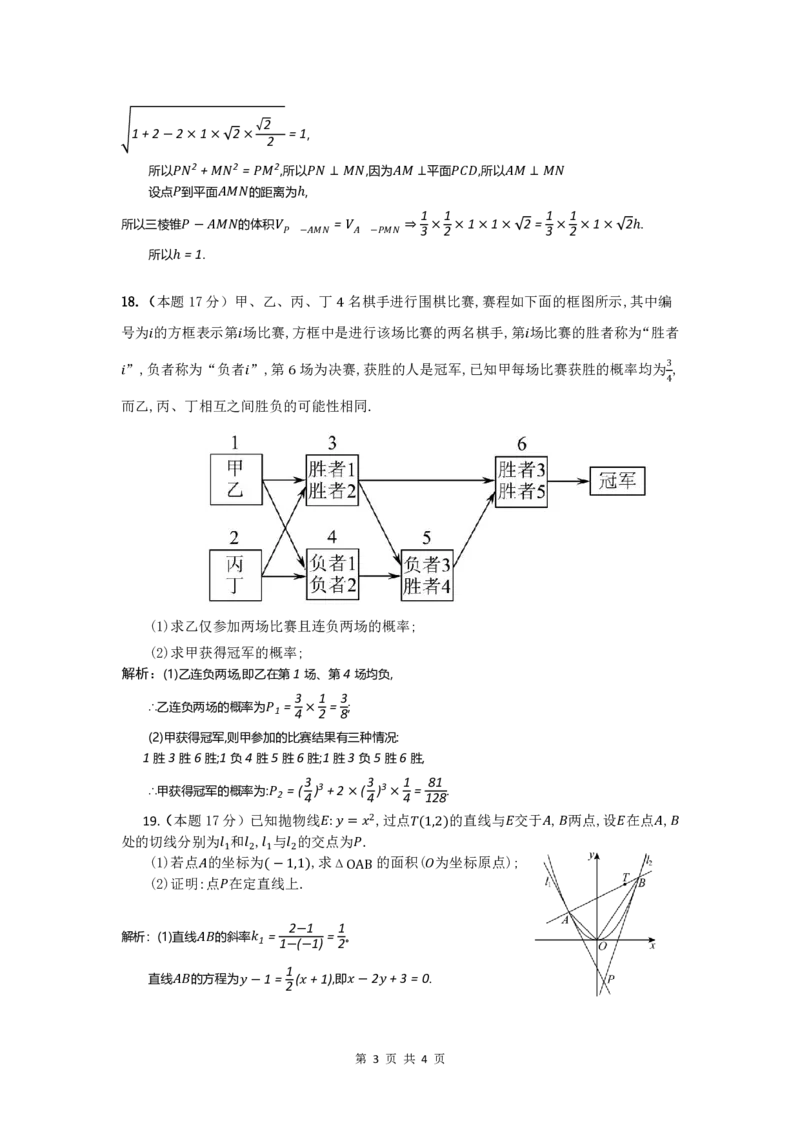
17(. 本题15分)已知在四棱锥 中, 平面 ,四边形 是直角梯形,
, ,若 , ,点 为 的中点,点 为 的四等分点(靠近点
− ⊥ //
).
⊥ = =2 =2 2
(1)求证:平面 平面 ;
(2)求点 到平面 的距离.
⊥
解析:(1)在四棱锥 中, 平面 , 平面 ,
则 ,又 ,
− ⊥ ⊂
因为 = , , 平面 ,所以 平面 ,
⊥ ⊥
因为 平面 ,所以 ,
∩ ⊂ ⊥
因为 = ,点 为 中点,所以 ,
⊂ ⊥
因为 = , , 平面 ,
⊥
所以 平面 ,
∩ ⊂
因为 平面 ,所以平面 平面
⊥
(2)由(1)知 平面 ,又 平面 ,则 ,
⊂ ⊥
因为 ⊥, = =2 , ⊂=2 2 ,点 为 ⊥的 中点,
⊥
所以 =2 2 , = 2 , = 2+ 2 = 8+8=4,
因为 点 为 的四 等 分点(靠近点 ).
所以 =1,
因为 = , ,所以 =45
所以由余弦定理得 ∘
⊥ ∠
= 2+ 2 2 45 =
∘
− ∙
第 2 页 共 4 页
{#{QQABDYIEogigAIJAARgCQwUaCECQkAEACYgGBEAEsAAAwANABAA=}#}2
1+2 2 1 2 =1,
2
所以 − ×2+ × 2 = × 2,所以 ,因为 平面 ,所以
设点 到平面 的距离为 ,
⊥ ⊥ ⊥
1 1 1 1
所以三棱锥 的 体积 ℎ = 1 1 2= 1 2 .
3 2 3 2
所以 =−1. − − ⇒ × × × × × × × ℎ
ℎ
18.(本题17分)甲、乙、丙、丁 名棋手进行围棋比赛,赛程如下面的框图所示,其中编
号为 的方框表示第 场比赛,方框中是4 进行该场比赛的两名棋手,第 场比赛的胜者称为“胜者
”,负者称为“负者 ”,第 场为决赛,获胜的人是冠军,已知甲每场比赛获胜的概率均为 ,
3
而乙,丙、丁相互之间 胜负的 6 可能性相同. 4
(1)求乙仅参加两场比赛且连负两场的概率;
(2)求甲获得冠军的概率;
解析:(1)乙连负两场,即乙在第1场、第4场均负,
3 1 3
∴乙连负两场的概率为 = = ;
1 4 2 8
(2)甲获得冠军,则甲参加 的比赛×结果有三种情况:
1胜3胜6胜;1负4胜5胜6胜;1胜3负5胜6胜,
3 3 1 81
∴甲获得冠军的概率为: =( )3+2 ( )3 = .
2 4 4 4 128
19.(本题17分)已知 抛物线 × ,过×点 的直线与 交于 , 两点,设 在点 ,
处的切线分别为 和 , 与 的交点为 .2
: = (1,2)
(1)若点 的坐标为 ,求Δ 的面积( 为坐标原点);
1 2 1 2
(2)证明:点 在定直线上.
(−1,1) OAB
2 1 1
解析:(1)直线 的斜率 = = 。
1 1 ( 1) 2
−
1− −
直线 的方程为 1= ( +1),即 2 +3= 0.
2
− −
第 3 页 共 4 页
{#{QQABDYIEogigAIJAARgCQwUaCECQkAEACYgGBEAEsAAAwANABAA=}#}2 +3= 0
联立方程 ,整理得:2 2 3=0.
= 2
−
− −
1 3
设 , 2 , , 2 ,则 + = , = .
1 1 2 2 1 2 2 1 2 2
3 −
设直线 与 轴的交点为 ,则 0, .
2
1 3 1 3 3
= + = | |+ | |= | |
OAB OAD OBD 2 2 1 2 2 2 4 2 1
Δ 3 Δ Δ ×15 × × × −
= ( + )2 4 = .
4 1 2 1 2 8
(2)由 = 2,得 '=−2 .
的方程为: =2 ( )+ 2,整理得: =2 2.
1 1 1 1 1 1
同理可得 的方程为: =2 2.
2 − 2 2 −
+
= 2 − 2 = 1 2
设 , ,联立方程 1 1 ,解得 2 .
=2 2 − 2 2 = 1 2
因为点 (1,2)在抛物线内 部,可 知 直−线 的斜率存在 ,
设直线 的方程为 = 1 +2,与抛物线方程联立得: 2 + 2=0,
故 + = , = −2.所以 = , = 2,可 得− =2 − 2,
1 2 1 2 2
所 以点 在定 直线 =2 −2上. − −
−
第 4 页 共 4 页
{#{QQABDYIEogigAIJAARgCQwUaCECQkAEACYgGBEAEsAAAwANABAA=}#}