文档内容
2024-2025 学年浙江省四校高二下学期 3 月联考数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在平面直角坐标系xOy中,直线l:x+√3 y+1=0的倾斜角为( )
π π 2π 5π
A. B. C. D.
6 3 3 6
x2 y2
2.已知双曲线 − =1(m>0)的焦距为6,则m为( )
m 4
A. 5 B. 2√5 C. √5 D. 32
3.圆 : 与圆 : 的位置关系是( )
C x2+ y2=4 C (x+1) 2+(y+2) 2=9
1 2
A. 内含 B. 内切 C. 外离 D. 相交
lim f(1+Δx)−f(1)
4.如果函数 在 处的导数为 ,那么 ( )
y=f(x) x=1 1 x→0 =
2Δx
1
A. 1 B. C. 2 D. 4
2
5.将3个相同的红球和3个相同的黑球装入三个不同的袋中,每袋均装2个球,则不同的装法种数为( )
A. 6 B. 7 C. 15 D. 90
6.三个非零向量 ⃗a , ⃗b , ⃗c 则“ ⃗a , ⃗b , ⃗c 共面”是“⃗ c=λ ⃗ a+μ ⃗ b(λ,μ∈R) ”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
7.2025年这个寒假,国产AI助手DeepSeek在全球掀起一场科技风暴.DeepSeek在训练模型时会用到对
n
数似然函数来优化参数.假设某模型的对数似然函数为 ,其中 是模型参数, 是
L(w)=∑ln(wx +1) w x
i i
i=1
输入特征,为了最大化L(w),我们需要求解以下哪个方程( )
n n n n
A. 1 B. 1 C. w D. w
∑ =n ∑ =0 ∑ =0 ∑ =n
wx +1 wx +1 wx +1 wx +1
i=1 i i=1 i i=1 i i=1 i
8.已知 是椭圆 x2 y2 上的动点,若动点 到定点 的距离 的最小值为 ,则
Q M: + =1(0m>1,则C是椭圆
B. 若2>m>1,则C是焦点在x轴的椭圆
C. 若m<1,则C是焦点在y轴的双曲线
√2
D. 若m=3,则C是直线x=
2
π
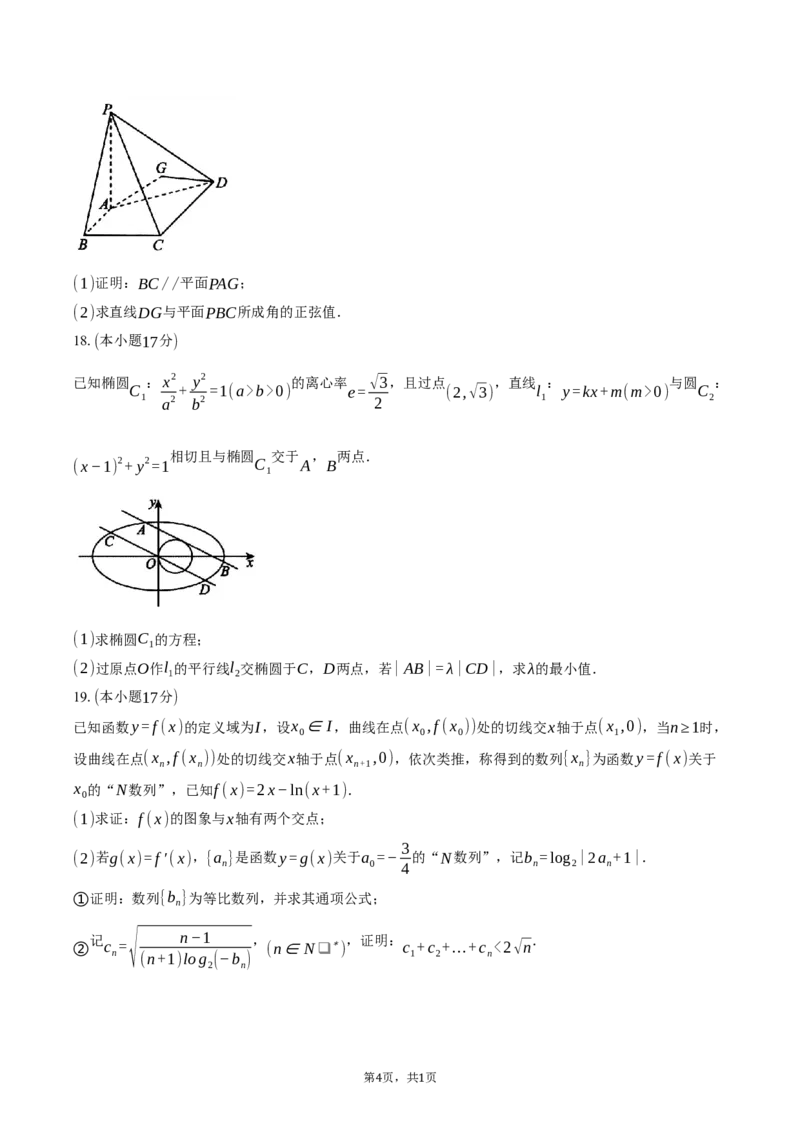
10.在平行六面体ABCD−A B C D 中,已知AB=AD=A A ,∠A AB=∠A AD=∠BAD= ,点
1 1 1 1 1 1 1 3
P为平面ABCD上的动点,则( )
A. 四边形B BDD 为矩形
1 1
⃗ ⃗ 1 ⃗
B. A A 在 AC 上的投影向量为 AC
1 1 3 1
√6
C. 点B到直线AC 的距离为
1 3
π
D. 若直线D P与直线AB所成的角为 ,则点P的轨迹为双曲线
1 3
11.如果一个人爬台阶的方式只有两种,在台阶底部(第0级)从下往上走,一次上一级台阶或一次上两级台
阶,设爬上n级台阶的方法数为a ,则下列结论正确的有( )
n
第 页,共 页
2 1A. 若用7步走完了10级台阶,则不同的走法有35种.
10
B.
∑a =231
i
i=1
C. a 是偶数
2025
D.
a2+a2+…+a2 =a a −1
1 2 2024 2024 2025
三、填空题:本题共3小题,每小题5分,共15分。
12.已知数列{a }为等比数列,a ·a ·a =216,则a =________.
n 1 3 11 5
13.阳春三月,草长莺飞;丝绦拂堤,尽飘香玉.三个家庭的3位妈妈带着3名女宝和2名男宝共8人踏春.
在沿行一条小溪时,为了安全起见,他们排队前进,三位母亲互不相邻照顾孩子;3名女宝相邻且不排最
前面也不排最后面;为了防止2名男宝打闹,2人不相邻,且不排最前面也不排最后面.则不同的排法种数
共有________种(用数字作答).
14.已知 , ,若对任意 ,都存在 ,使得
f(x)=lnx−ax g(x)=ex−ax x ∈(0,+∞) x ∈(0,+∞)
1 2
f(x )g(x )=x x ,则实数a的取值范围为________.
1 2 1 2
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
x−1
已知函数f(x)=lnx−a⋅ 的图象在点(1,f(1))处的切线与直线y=3平行,其中a为常数.
x+1
(1)求a的值;
求不等式 的解集.
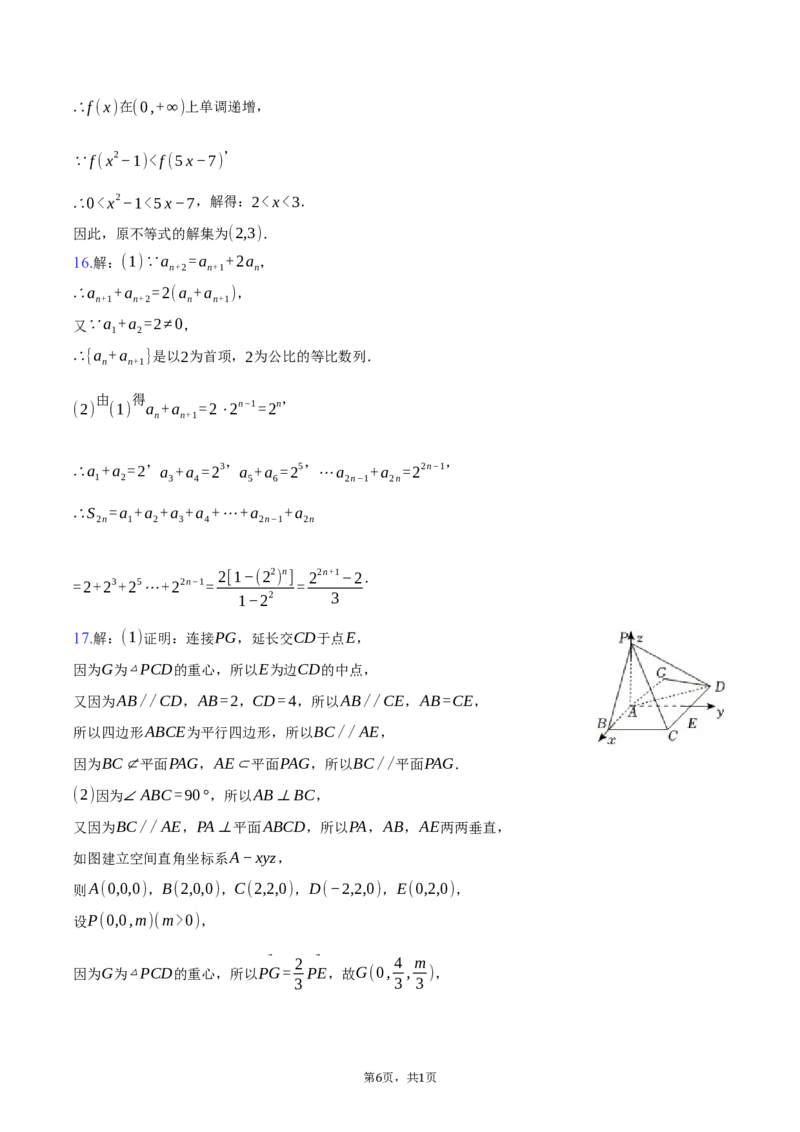
(2) f(x2−1)b>0) e= (2,√3) l y=kx+m(m>0) C
1 a2 b2 2 1 2
相切且与椭圆 交于 , 两点.
(x−1) 2+ y2=1 C A B
1
(1)求椭圆C 的方程;
1
(2)过原点O作l 的平行线l 交椭圆于C,D两点,若|AB|=λ|CD|,求λ的最小值.
1 2
19.(本小题17分)
已知函数y=f(x)的定义域为I,设x ∈I,曲线在点(x ,f(x ))处的切线交x轴于点(x ,0),当n≥1时,
0 0 0 1
设曲线在点(x ,f(x ))处的切线交x轴于点(x ,0),依次类推,称得到的数列{x }为函数y=f(x)关于
n n n+1 n
x 的“N数列”,已知f(x)=2x−ln(x+1).
0
(1)求证:f(x)的图象与x轴有两个交点;
3
(2)若g(x)=f ′(x),{a }是函数y=g(x)关于a =− 的“N数列”,记b =log |2a +1|.
n 0 4 n 2 n
①证明:数列{b }为等比数列,并求其通项公式;
n
记 √ n−1 , ,证明: .
② c = (n∈N❑∗) c +c +…+c <2√n
n (n+1)log (−b ) 1 2 n
2 n
第 页,共 页
4 11.D
2.A
3.D
4.B
5.B
6.B
7.A
8.C
9.BC
10.ABD
11.ABD
12.6
13.288
1
14.[e+ ,+∞)
e
15.解: 1 x+1−(x−1) 1 2 , a,
(1)f′ (x)= −a = −a ∴f′ (1)=1−
x (x+1) 2 x (x+1) 2 2
x−1
∵函数f(x)=lnx−a⋅ 在点(1,f(1))处的切线与直线y=3平行,
x+1
a
∴f′ (1)=1− =0,∴a=2.
2
x−1
(2)∵函数f(x)=lnx−a⋅ 的定义域为(0,+∞),
x+1
由{x2−1>0可得 7 ,
x∈( ,+∞)
5x−7>0 5
1 4 (x−1) 2
∵f′ (x)= − = ≥0
x (x+1) 2 x(x+1) 2
第 页,共 页
5 1∴f(x)在(0,+∞)上单调递增,
,
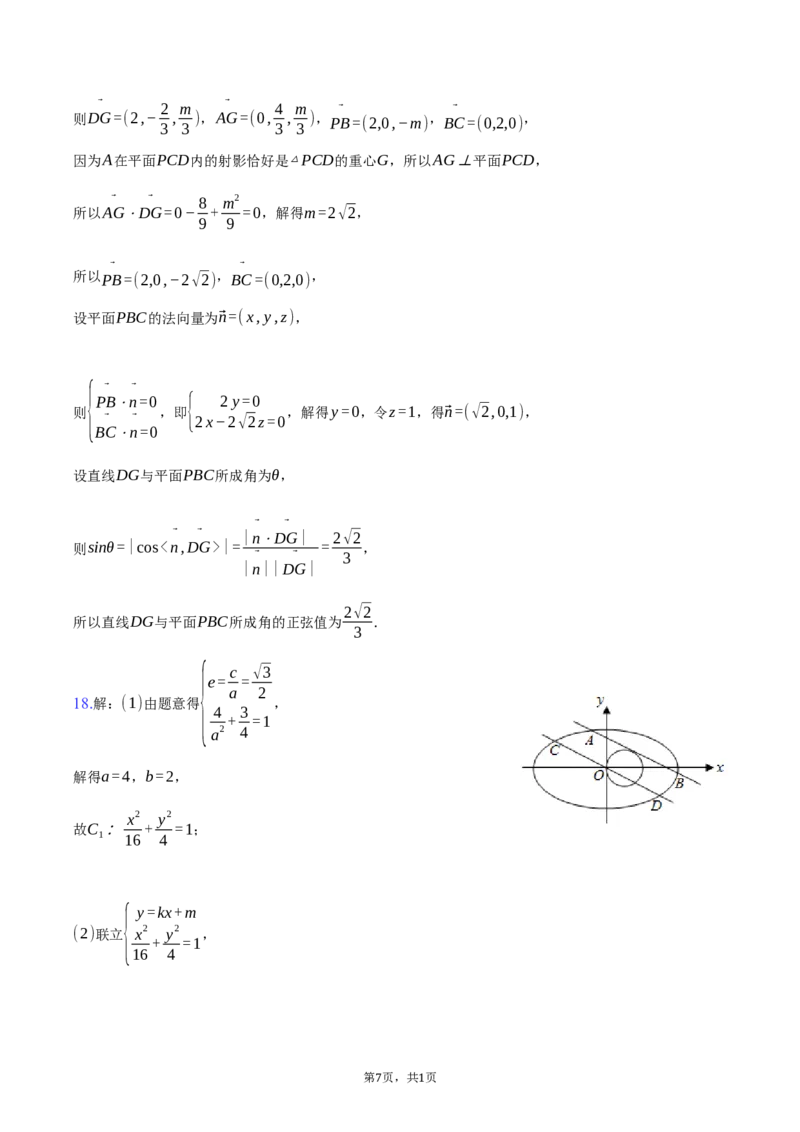
∵f(x2−1)0),
⃗ 2 ⃗ 4 m
因为G为△PCD的重心,所以PG= PE,故G(0, , ),
3 3 3
第 页,共 页
6 1⃗ 2 m ⃗ 4 m ⃗ ⃗
则DG=(2,− , ),AG=(0, , ),PB=(2,0,−m) ,BC=(0,2,0) ,
3 3 3 3
因为A在平面PCD内的射影恰好是△PCD的重心G,所以AG⊥平面PCD,
⃗ ⃗ 8 m2
所以AG⋅DG=0− + =0,解得m=2√2,
9 9
⃗ ⃗
所以PB=(2,0,−2√2) ,BC=(0,2,0) ,
设平面PBC的法向量为⃗n=(x,y,z),
{ ⃗ ⃗
PB⋅n=0 { 2y=0
则 ,即 ,解得y=0,令z=1,得⃗n=(√2,0,1),
⃗ ⃗ 2x−2√2z=0
BC⋅n=0
设直线DG与平面PBC所成角为θ,
⃗ ⃗
⃗ ⃗ |n⋅DG| 2√2
则sinθ=|cos|= = ,
⃗ ⃗ 3
|n||DG|
2√2
所以直线DG与平面PBC所成角的正弦值为 .
3
{ e= c = √3
a 2
18.解:(1)由题意得 ,
4 3
+ =1
a2 4
解得a=4,b=2,
x2 y2
故C : + =1;
1 16 4
{
y=kx+m
(2)联立 x2 y2 ,
+ =1
16 4
第 页,共 页
7 1化简得(1+4k2 )x2+8kmx+4(m2−4)=0,
△>0恒成立,
设A(x ,y ),B(x ,y ),
1 1 2 2
8km
{x +x =−
1 2 1+4k2 4√16k2−m2+4
则 ,得|x −x |= ,
4(m2−4) 1 2 1+4k2
x x =
1 2 1+4k2
4√16k2−m2+4
∴|AB|=√1+k2
⋅ ,
1+4k2
把l :y=kx代入C :
x2
+
y2
=1,得x2=
16
,
2 1 16 4 1+4k2
8
∴|CD|=√1+k2
⋅ ,
√1+4k2
又直线l :y=kx+m(m>0)与圆C :(x−1) 2+ y2=1相切,
1 2
|m+k| 1−m2
则
=1化简得:k=
,
√k2+1 2m
|AB| √16k2−m2+4 1√ m2
∴λ= = = 4−
|CD| 2√1+4k2 2 1+4k2
第 页,共 页
8 11√ m2 1√ m4 1√ 1 √6
= 4− = 4− = 4− ≥
2
1+4(
1−m2
) 2
2 m4−m2+1 2
(
1
−
1
) 2+
3 3 ,
2m m2 2 4
√2 √6
当m=√2,k=− 时,λ取最小值 .
4 3
1 2x+1
19.解:(1)由题意知, f ′(x)=2− = ,
x+1 x+1
1 1
当 x∈(−1,− ),f ′(x)<0,f(x) 单调递减;当 x∈(− ,+∞),f ′(x)>0,f(x) 单调递增,
2 2
1
所以 f(x) =f(− )=−1+ln2<0 ,
min 2
1 1 1 2
因为 f( −1)=2( −1)−ln = >0 (或者:当 x>−1,x→−1 时, f(x)→+∞ ),
e2 e2 e2 e2
f(e−1)=2(e−1)−lne=2e−3>0 (或者: f(0)=0 ),
1 1
所以 f(x) 在 (−1,− ) 和 (− ,+∞) 上各有一个零点,
2 2
即 f(x) 的图象与 x 轴有两个交点.
1 2x+1
(2)① g(x)=f′ (x)=2− = ,
x+1 x+1
1
g′ (x)=
(x+1) 2
则在 处的切线斜率为
(a ,g(a ))
n n
g′(a )=
1 ,
n (a +1) 2
n
2a +1 1
所以在 (a ,g(a )) 处的切线方程为 y− n = (x−a ) ,
n n a +1 (a +1) 2 n
n n
令
y=0
,解得
a =a −(2a +1)(a +1)=−2a2−2a −1
,
n+1 n n n n n
所以
−(2a +1)=(2a +1) 2
,所以
b =log |2a +1|=2log |2a +1|=2b
,
n+1 n n+1 2 n+1 2 n n
第 页,共 页
9 1即 b
n+1=2,b =2log |2a +1|=2log
1
=−2
,
b 1 2 0 22
n
所以 是以首项为 ,公比为 的等比数列,所以 .
{b } −2 2 b =−2n
n n
由 √ n−1 √1 2 2 ,
② c = < = < =2(√n−√n−1)
n n(n+1) n √n+√n √n+√n−1
则 .
c +c +⋅⋅⋅+c <2(√1−0)+2(√2−√1)+⋅⋅⋅+2(√n−√n−1)=2√n
1 2 n
第 页,共 页
10 1