文档内容
第一章 空间向量与立体几何全章综合测试卷(基础篇)
参考答案与试题解析
一.选择题(共8小题,满分40分,每小题5分)
1.(5分)(2023·江苏·高二专题练习)下列说法正确的是( )
A.任一空间向量与它的相反向量都不相等
B.不相等的两个空间向量的模必不相等
C.同平面向量一样,任意两个空间向量都不能比较大小
D.将空间向量所有的单位向量平移到同一起点,则它们的终点构成一个圆
【解题思路】取零向量可判断A选项;利用任意一个非零向量与其相反向量可判断B选项;利用向量不能
比大小可判断C选项;利用单位向量的概念可判断D选项.
【解答过程】对于A选项,零向量与它的相反向量相等,A错;
对于B选项,任意一个非零向量与其相反向量不相等,但它们的模相等,B错;
对于C选项,同平面向量一样,任意两个空间向量都不能比较大小,C对;
对于D选项,将空间向量所有的单位向量平移到同一起点,则它们的终点构成一个球,D错.
故选:C.
2.(5分)(2023春·江苏常州·高二校考阶段练习)如图,M是四面体OABC的棱BC的中点,点N在线
1 3
段OM上,点P在线段AN上,且MN= ON,AP= AN,用向量⃗OA,⃗OB,⃗OC表示⃗OP,则⃗OP=
2 4
( )
1 1 1 1 3 1
A. ⃗OA+ ⃗OB+ ⃗OC B. ⃗OA− ⃗OB+ ⃗OC
4 4 4 4 4 4
1 1 3 1 3 1
C. ⃗OA− ⃗OB+ ⃗OC D. ⃗OA+ ⃗OB+ ⃗OC
4 4 4 4 4 4
【解题思路】根据空间向量的线性运算求得正确答案.
学科网(北京)股份有限公司3
【解答过程】⃗OP= =⃗OA+⃗AP=⃗OA+ ⃗AN
4
3 1 3
=⃗OA+ (⃗ON−⃗OA)= ⃗OA+ ⃗ON
4 4 4
1 3 2 1 1
= ⃗OA+ × ⃗OM= ⃗OA+ ⃗OM
4 4 3 4 2
1 1 1 1 1 1
= ⃗OA+ × (⃗OB+⃗OC)= ⃗OA+ ⃗OB+ ⃗OC.
4 2 2 4 4 4
故选:A.
3.(5分)(2023·全国·高三对口高考)已知 ,
⃗a=(1,1,0),⃗b=(0,1,1),⃗c=(1,0,1),⃗p=⃗a−⃗b,⃗q=⃗a+2⃗b−⃗c
则⃗p⋅⃗q=( )
A.−1 B.1 C.0 D.2
【解题思路】根据空间向量的坐标运算与数量积的运算法则,求解即可.
【解答过程】因为 ,
⃗a=(1,1,0),⃗b=(0,1,1),⃗c=(1,0,1)
所以⃗p=⃗a−⃗b =(1,1,0)−(0,1,1)=(1,0,−1),
⃗q=⃗a+2⃗b−⃗c =(1,1,0)+2(0,1,1)−(1,0,1)=(0,3,1),
则⃗p⋅⃗q= 1×0+0×3−1×1=−1.
故选:A.
4.(5分)(2023秋·山西大同·高二校考期末)已知空间向量 ,且 ,则向量
⃗a=(1,0,1),⃗b=(x,1,2) ⃗a⋅⃗b=3
⃗a与⃗b的夹角为( )
5π 2π π π
A. B. C. D.
6 3 3 6
【解题思路】利用空间向量的坐标运算,求出向量⃗a与⃗b的夹角的余弦值,进而可求夹角.
【解答过程】因为 ,所以 ,所以 ,
⃗a⋅⃗b=x+0+2=3 x=1 ⃗b=(1,1,2)
则有
|⃗a|=√1+1=√2,|⃗b|=√1+1+4=√6,
所以 cos<⃗a,⃗b>= ⃗a⋅⃗b = 3 = √3,
|⃗a||⃗b| √2×√6 2
π
因为<⃗a,⃗b>∈[0,π],所以<⃗a,⃗b>= ,
6
学科网(北京)股份有限公司故选:D.
5.(5分)(2023秋·陕西宝鸡·高二统考期末)已知 ,则下
⃗a=(2,3,−1),⃗b=(2,0,−4),⃗c=(−4,−6,2)
列结论正确的是( )
A.⃗a⊥⃗b B.⃗a⊥⃗c C.⃗a//⃗b D.⃗a//⃗c
【解题思路】根据向量平行、垂直的坐标表示直接判断即可.
【解答过程】因为 ,
⃗a⋅⃗b=2×2+3×0+(−1)×(−4)=8
⃗a⋅⃗c=2×(−4)+3×(−6)+(−1)×2=−28,
所以AB错误;
2 0 −4
因为 ≠ ≠ ,所以⃗a,⃗b不平行,C错误;
2 3 −1
−4 −6 2
因为 = = ,所以⃗a//⃗c,D正确.
2 3 −1
故选:D.
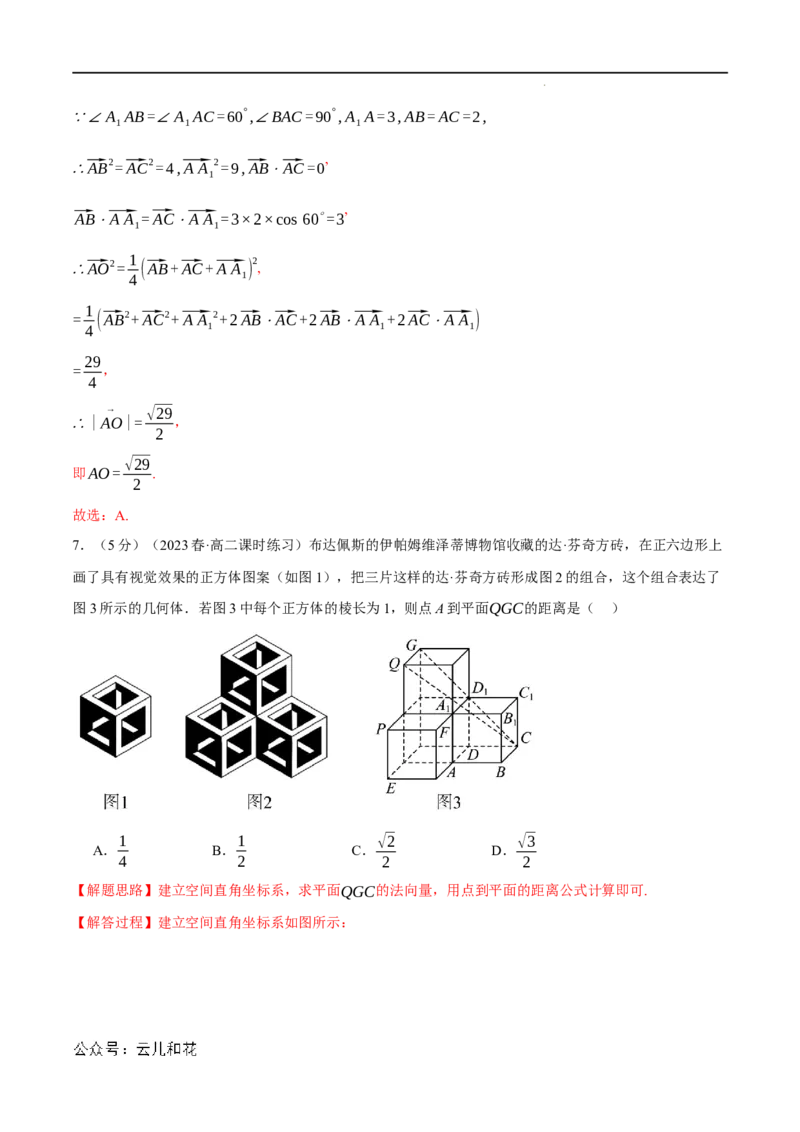
6.(5分)(2023春·江苏南通·高二校考阶段练习)如图,在三棱柱ABC-ABC 中,BC 与BC相交于点
1 1 1 1 1
O,∠AAB=∠AAC=60∘,∠BAC=90∘,AA=3,AB=AC=2,则线段AO的长度为( )
1 1 1
√29 √23
A. B.√29 C. D.√23
2 2
【解题思路】用
⃗AB,⃗AC,⃗A A 1
表示出
A
→
O
,计算
A
→
O2
,开方得出AO的长度.
【解答过程】因为四边形BCC B 是平行四边形,
1 1
1 1
∴⃗BO= ⃗BC = (⃗BC+⃗BB ),
2 1 2 1
1 1 1 1 1
∴⃗AO=⃗AB+⃗BO=⃗AB+ ⃗BC+ ⃗A A = ⃗AC+ ⃗AB+ ⃗A A
2 2 1 2 2 2 1
学科网(北京)股份有限公司∵∠A AB=∠A AC=60°,∠BAC=90°,A A=3,AB=AC=2,
1 1 1
,
∴⃗AB2=⃗AC2=4,⃗A A 2=9,⃗AB⋅⃗AC=0
1
,
⃗AB⋅⃗A A =⃗AC⋅⃗A A =3×2×cos60∘=3
1 1
∴⃗AO2= 1 (⃗AB+⃗AC+⃗A A ) 2 ,
4 1
1
= (⃗AB2+⃗AC2+⃗A A 2+2⃗AB⋅⃗AC+2⃗AB⋅⃗A A +2⃗AC⋅⃗A A )
4 1 1 1
29
= ,
4
→ √29
∴|AO|= ,
2
√29
即AO= .
2
故选:A.
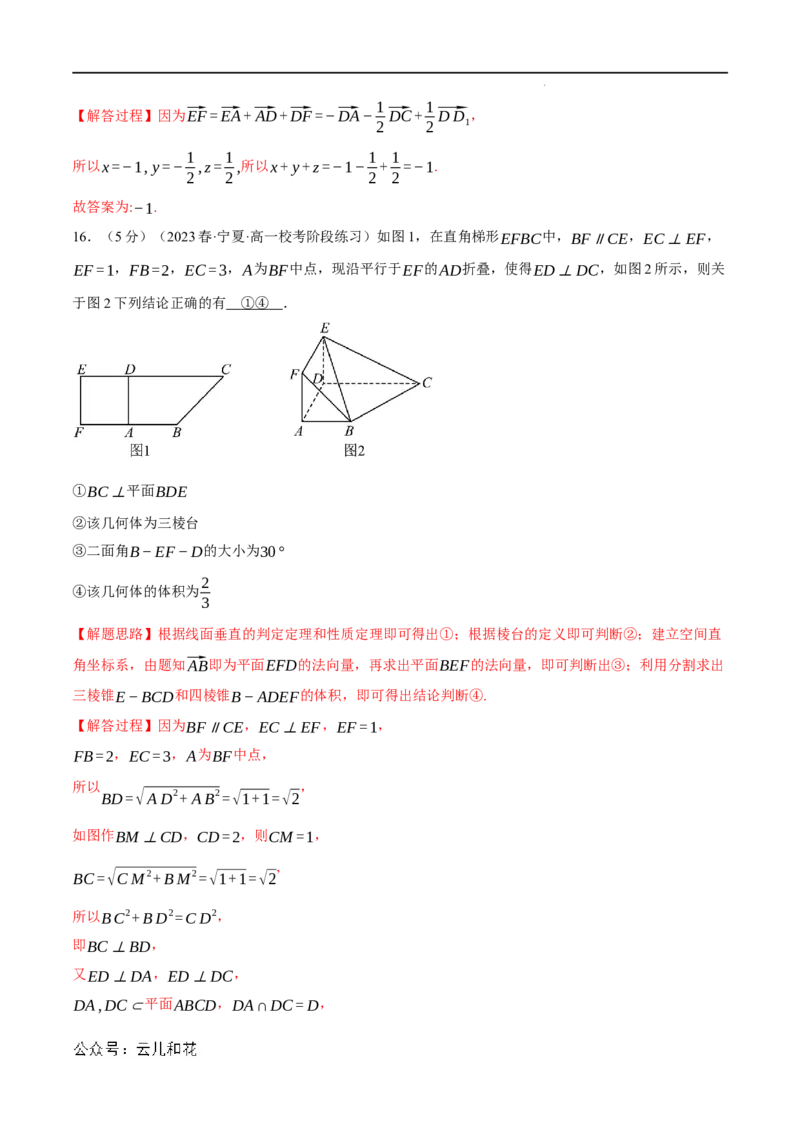
7.(5分)(2023春·高二课时练习)布达佩斯的伊帕姆维泽蒂博物馆收藏的达·芬奇方砖,在正六边形上
画了具有视觉效果的正方体图案(如图1),把三片这样的达·芬奇方砖形成图2的组合,这个组合表达了
图3所示的几何体.若图3中每个正方体的棱长为1,则点A到平面QGC的距离是( )
1 1 √2 √3
A. B. C. D.
4 2 2 2
【解题思路】建立空间直角坐标系,求平面QGC的法向量,用点到平面的距离公式计算即可.
【解答过程】建立空间直角坐标系如图所示:
学科网(北京)股份有限公司则C(0,2,0),Q(1,0,2),G(0,0,2),A(1,1,0),⃗QC=(−1,2,−2),⃗QG=(−1,0,0),⃗AC=(−1,1,0),
设平面QGC的法向量为⃗n=(x,y,z),则¿,即¿,则平面QGC的一个法向量为⃗n=(0,1,1),
则点A到平面 的距离 |⃗n⋅⃗AC| √2.
QGC d= =
|⃗n| 2
故选:C.
8.(5分)(2023秋·高一单元测试)如图,在平行六面体ABCD−A B C D 中,以顶点A为端点的三
1 1 1 1
条棱长均为6,且它们彼此的夹角都是60∘,下列说法中正确的是( )
A.
AC =12√6
1
√6
B.直线BD 与AC所成角的正弦值为
1 6
C.向量 与 的夹角是
⃗B C ⃗A A 60∘
1 1
D.AC ⊥平面CB D
1 1 1
【解题思路】利用基底向量,结合向量模长公式即可判断A,利用向量的夹角公式即可判断BC,由向量垂直
即可得线线垂直,进而根据线面垂直的判断即可判断D.
1
【解答过程】由题意可得|⃗AB|=|⃗A A |=|⃗AD|=6,⃗AB⋅⃗AD=⃗AB⋅⃗A A =⃗AD⋅⃗A A =6×6× =18,
1 1 1 2
又 ,则
⃗AC =⃗AB+⃗AD+⃗A A |⃗AC |=√(⃗AB+⃗AD+⃗A A ) 2
1 1 1 1
学科网(北京)股份有限公司,
=√⃗AB2+⃗AD2+⃗A A 2+2⃗AB⋅⃗AD+2⃗AD⋅⃗A A +2⃗AB⋅⃗A A =√3×62+3×2×6×6×cos60°=6√6
1 1 1
故A错误,
由于 ,
⃗BD =⃗AD+⃗A A −⃗AB,⃗AC=⃗AB+⃗AD
1 1
则
|⃗BD |=|⃗AD+⃗A A −⃗AB|==√⃗AD2+⃗A A 2+⃗AB2+2⃗AD⋅⃗A A −2⃗AB⋅⃗A A −2⃗AB⋅⃗AD=√3×36−2×18=6√2
1 1 1 1 1
,
|⃗AC|=|⃗AB+⃗AD|=√⃗AB2+⃗AD2+2⃗AB⋅⃗AD=√36×2+2×18=6√3
又
⃗BD ⋅⃗AC=(⃗AD+⃗A A −⃗AB)⋅(⃗AB+⃗AD)=⃗AD⋅⃗AB+⃗A A ⋅⃗AB−⃗AB2+⃗AD2+⃗A A ⋅⃗AD−⃗AB⋅⃗AD=36
1 1 1 1
则 cos<⃗BD ,⃗AC>= ⃗BD 1 ⋅⃗AC = 36 = √6,故B错误,
1 |⃗BD ||⃗AC| 6√2×6√3 6
1
由于 ,所以向量 与 的夹角即为 与 的夹角,
BB //A A ⃗B C ⃗A A ⃗B C ⃗BB
1 1 1 1 1 1
由于 等边三角形,故 为 ,
|BB |=|BC|=6,∠CBB =60∘,∴△CBB ∠BB C 60∘
1 1 1 1
进而 与 的夹角为 的补角,故 与 的夹角为 ,故C错误,
⃗B C ⃗BB ∠BB C ⃗B C ⃗BB 120∘
1 1 1 1 1
⃗AC ⋅⃗B C=(⃗AB+⃗AD+⃗A A )⋅(⃗AD−⃗A A )=⃗AB⋅⃗AD+⃗AD2+⃗A A ⋅⃗AD−⃗AB⋅⃗A A −⃗A A ⋅⃗AD−⃗A A 2=0
1 1 1 1 1 1 1 1
⃗AC ⋅⃗B D =(⃗AB+⃗AD+⃗A A )⋅(⃗AD−⃗AB)=⃗AB⋅⃗AD+⃗AD2+⃗A A ⋅⃗AD−⃗AB⋅⃗AD−⃗A A ⋅⃗AB−⃗AB2=0
1 1 1 1 1 1
,
所以 ,进而可得
⃗AC ⊥⃗B C,⃗AC ⊥⃗B D AC ⊥B C,AC ⊥B D ,B C∩B D =B ,B C,B D ⊂
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
平面CB D ,
1 1
故AC ⊥ 平面CB D ,故D正确,
1 1 1
故选:D.
二.多选题(共4小题,满分20分,每小题5分)
学科网(北京)股份有限公司9.(5分)(2023·全国·高一专题练习)给出下列命题,其中正确的命题是( )
A.若 ,则 或
|⃗a|=|⃗b| ⃗a=⃗b ⃗a=−⃗b
B.若向量 是向量 的相反向量,则
⃗a ⃗b |⃗a|=|⃗b|
C.在正方体 中,
ABCD−A B C D ⃗AC=⃗A C
1 1 1 1 1 1
D.若空间向量⃗m ,⃗n ,⃗p 满足⃗m=⃗n ,⃗n=⃗p ,则⃗m=⃗p
【解题思路】根据向量模长,相等向量,相反向量概念逐项判断真假.
【解答过程】对于选项A:若 ,即向量 与 的模相等,但方向不确定,故A错误;
|⃗a|=|⃗b| ⃗a ⃗b
对于选项B:相反向量是指大小相等方向相反的两个向量,故B正确;
对于选项C:在正方体 中, 与 大小相等,方向相同,故 ,所以
ABCD−A B C D ⃗AC ⃗A C ⃗AC=⃗A C
1 1 1 1 1 1 1 1
C正确;
对于选项D:若⃗m=⃗n ,⃗n=⃗p,则⃗m,⃗p方向相同大小相等,故⃗m=⃗p,若⃗m,⃗n,⃗p中有零向量结论也正确,
所以D正确.
故选:BCD.
10.(5分)(2023春·江苏盐城·高二校考阶段练习)以下能判定空间四点P、M、A、B共面的条件是(
)
1 1 1
A.⃗MP=2⃗MA+3⃗MB B.⃗OP= ⃗OA+ ⃗OB+ ⃗OM
2 3 6
C.⃗PM⋅⃗AB=0 D.⃗PM ∥ ⃗AB
【解题思路】根据空间向量的相关概念结合四点共面的结论逐项分析判断.
【解答过程】对A:若⃗MP=2⃗MA+3⃗MB,结合向量基本定理知:⃗MP,⃗MA,⃗MB为共面向量,故四点
P、M、A、B共面,A正确;
1 1 1 1 1 1
对B:若⃗OP= ⃗OA+ ⃗OB+ ⃗OM,且 + + =1,结合向量共面的性质知:四点P、M、A、B共面,
2 3 6 2 3 6
B正确;
对C:若⃗PM⋅⃗AB=0,则PM⊥AB,可知直线PM,AB的位置关系:异面或相交,故四点P、M、A、B
不一定共面,C错误;
对D:若⃗PM ∥ ⃗AB,可知直线PM,AB的位置关系:平行或重合,故四点P、M、A、B共面,D正确;
故选:ABD.
学科网(北京)股份有限公司11.(5分)(2023秋·湖北襄阳·高二校考期末)已知向量 , ,则下列结
⃗a=(1,−1,m) ⃗b=(−2,m−1,2)
论中正确的是( )
A.若|⃗a|=2,则m=±√2
B.若⃗a⊥⃗b,则m=−1
C.不存在实数 ,使得⃗a=λ⃗b
D.若 ,则
⃗a⋅⃗b=−1 ⃗a+⃗b=(−1,−2,2)
【解题思路】运用空间向量的垂直、共线的表示及应用,以及空间向量的数量积的运算、模的运算,逐项
判断即可.
【解答过程】对于A项,由 可得 ,解得 ,故A项正确;
|⃗a|=2 √12+(−1) 2+m2=2 m=±√2
对于B项,由⃗a⊥⃗b可得⃗a⋅⃗b=−2+1−m+2m=0,解得m=1,故B项错误;
对于C项,假设存在实数λ,使得⃗a=λ⃗b,则¿,所以不存在实数λ,使得⃗a=λ⃗b,故C项正确;
对于D项,由 可得 ,解得 ,所以 ,故D项正确.
⃗a⋅⃗b=−1 −2+1−m+2m=−1 m=0 ⃗a+⃗b=(−1,−2,2)
故选:ACD.
12.(5分)(2023秋·浙江丽水·高二统考期末)在棱长为2的正方体ABCD−A B C D 中,P,Q分
1 1 1 1
别是棱BC,CC 的中点,点M满足⃗BM=t⃗BA,t∈[0,1],下列结论正确的是( )
1
A.若t=1,则A B //平面MPQ
1 1
9
B.若t=1,则过点M,P,Q的截面面积是
2
1 √3
C.若t= ,则点A 到平面MPQ的距离是
2 1 6
1 √2
D.若t= ,则AB与平面MPQ所成角的正切值为
2 2
【解题思路】t=1时有M与A重合,对于A选项,可以利用反证法判定;对于B选项,根据平面的性质计
1
算即可;t= 时,M为AB中点,对于CD选项,建立合适的空间直角坐标系,利用空间向量处理即可.
2
【解答过程】如图所示,t=1时有M与A重合,
对于A选项,延长PQ交BB 于L,连接AL,易得平面AB ∩平面MPQ=AL,若A B //平面MPQ,则
1 1 1 1
A B ∥AL,显然A B ∥AB,且B、L不重合,矛盾,故A错误;
1 1 1 1
对于B项,连接AD、DQ,易知平面APQD 即该截面,显然该截面为等腰梯形,易得
1 1 1
学科网(北京)股份有限公司PQ=√2=
1
AD ,D Q=AP=√5
,
S=
1
(√2+2√2)×
√
5−
(√2) 2
=
9,故B正确;
2 1 1 2 2 2
1
如图所示,t= 时,M为AB中点,以D为中心建立空间直角坐标系,
2
则M(2,1,0)、P(1,2,0)、Q(0,2,1)、A (2,0,2)、A(2,0,0)、B(2,2,0),
1
,
⃗MP=(−1,1,0),⃗MQ=(−2,1,1),⃗M A =(0,−1,2),⃗MB=(0,1,0)
1
设平面MPQ的法向量为⃗n=(x,y,z),则¿,
令x=1,则y=1=z,故⃗n=(1,1,1)
对于C项,设点
A
到平面MPQ的距离为
d
,则
d=
|⃗M A
1
⋅⃗n|
=
√3,即C错误;
1 |⃗n| 3
对于D项,设AB与平面MPQ所成角为 α ,则 sinα=|cos⟨⃗n,⃗MB⟩|=
|⃗n⋅⃗MB|
=
√3
,
|⃗n||⃗MB| 3
√6 √2
所以cosα= ,tanα= ,即D正确.
3 2
故选:BD.
三.填空题(共4小题,满分20分,每小题5分)
学科网(北京)股份有限公司13.(5分)(2023秋·上海浦东新·高二校考期末)已知 , ,则 2 4 .
⃗a=(1,2,3) ⃗b=(3,2,1) ⃗a⋅(⃗a+⃗b)=
【解题思路】利用向量的数量积直接求解.
【解答过程】因为 , ,
⃗a=(1,2,3) ⃗b=(3,2,1)
所以 .
⃗a+⃗b=(4,4,4)
所以 .
⃗a⋅(⃗a+⃗b)=1×4+2×4+3×4=24
故答案为:24.
14.(5分)(2023·高二校考课时练习)已知 , ,且 与 的夹角为钝角,
⃗a=(3,−2,−3) ⃗b=(−1,x−1,1) ⃗a ⃗b
( 5) (5 )
则x的取值范围是 −2, ∪ ,+∞ .
3 3
【解题思路】由⃗a⋅⃗b<0求解,再排除⃗a与⃗b共线时x的值即可得答案.
【解答过程】因为⃗a与⃗b的夹角为钝角,
,解得 ,
∴⃗a⋅⃗b=−3−2(x−1)−3<0 x>−2
−1 x−1 5
由题意得⃗a与⃗b不共线,则 ≠ ,解得x≠ ,
3 −2 3
( 5) (5 )
∴x的取值范围是 −2, ∪ ,+∞ .
3 3
( 5) (5 )
故答案为: −2, ∪ ,+∞ .
3 3
15.(5分)(2023春·云南·高二校联考阶段练习)如图,在正方体ABCD−A B C D 中,E,F分别为
1 1 1 1
的中点,若 ,则 .
AB,DD ⃗EF=x⃗DA+ y⃗DC+z⃗DD x+ y+z= −1
1 1
【解题思路】根据向量的分解和基底的定义求解.
学科网(北京)股份有限公司1 1
【解答过程】因为⃗EF=⃗EA+⃗AD+⃗DF=−⃗DA− ⃗DC+ ⃗DD ,
2 2 1
1 1 1 1
所以x=−1,y=− ,z= ,所以x+ y+z=−1− + =−1.
2 2 2 2
故答案为:−1.
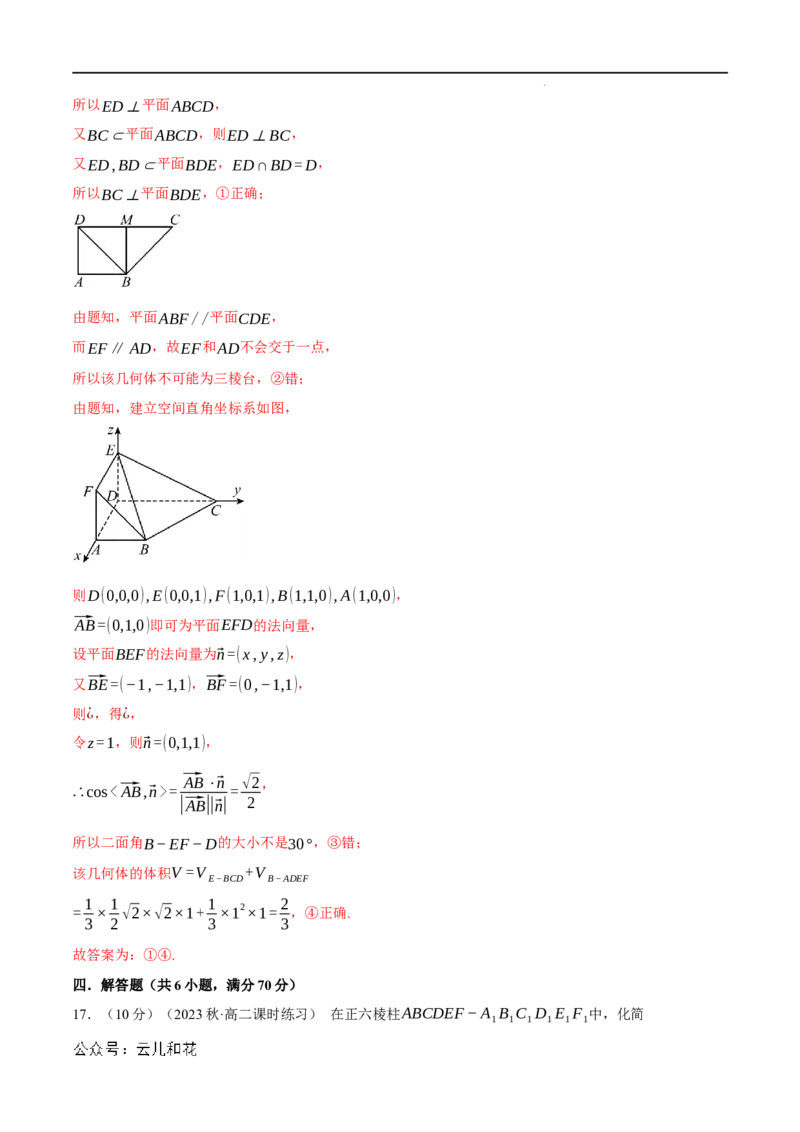
16.(5分)(2023春·宁夏·高一校考阶段练习)如图1,在直角梯形EFBC中,BF∥CE,EC⊥EF,
EF=1,FB=2,EC=3,A为BF中点,现沿平行于EF的AD折叠,使得ED⊥DC,如图2所示,则关
于图2下列结论正确的有 ①④ .
①BC⊥平面BDE
②该几何体为三棱台
③二面角B−EF−D的大小为30°
2
④该几何体的体积为
3
【解题思路】根据线面垂直的判定定理和性质定理即可得出①;根据棱台的定义即可判断②;建立空间直
角坐标系,由题知⃗AB即为平面EFD的法向量,再求出平面BEF的法向量,即可判断出③;利用分割求出
三棱锥E−BCD和四棱锥B−ADEF的体积,即可得出结论判断④.
【解答过程】因为BF∥CE,EC⊥EF,EF=1,
FB=2,EC=3,A为BF中点,
所以 ,
BD=√AD2+AB2=√1+1=√2
如图作BM⊥CD,CD=2,则CM=1,
,
BC=√CM2+BM2=√1+1=√2
所以BC2+BD2=CD2,
即BC⊥BD,
又ED⊥DA,ED⊥DC,
DA,DC⊂平面ABCD,DA∩DC=D,
学科网(北京)股份有限公司所以ED⊥平面ABCD,
又BC⊂平面ABCD,则ED⊥BC,
又ED,BD⊂平面BDE,ED∩BD=D,
所以BC⊥平面BDE,①正确;
由题知,平面ABF//平面CDE,
而EF∥AD,故EF和AD不会交于一点,
所以该几何体不可能为三棱台,②错;
由题知,建立空间直角坐标系如图,
则D(0,0,0),E(0,0,1),F(1,0,1),B(1,1,0),A(1,0,0),
⃗AB=(0,1,0)即可为平面EFD的法向量,
设平面BEF的法向量为⃗n=(x,y,z),
又⃗BE=(−1,−1,1),⃗BF=(0,−1,1),
则¿,得¿,
令z=1,则⃗n=(0,1,1),
⃗AB⋅⃗n √2,
∴cos<⃗AB,⃗n>= =
|⃗AB||⃗n| 2
所以二面角B−EF−D的大小不是30°,③错;
该几何体的体积V =V +V
E−BCD B−ADEF
1 1 1 2
= × √2×√2×1+ ×12×1= ,④正确.
3 2 3 3
故答案为:①④.
四.解答题(共6小题,满分70分)
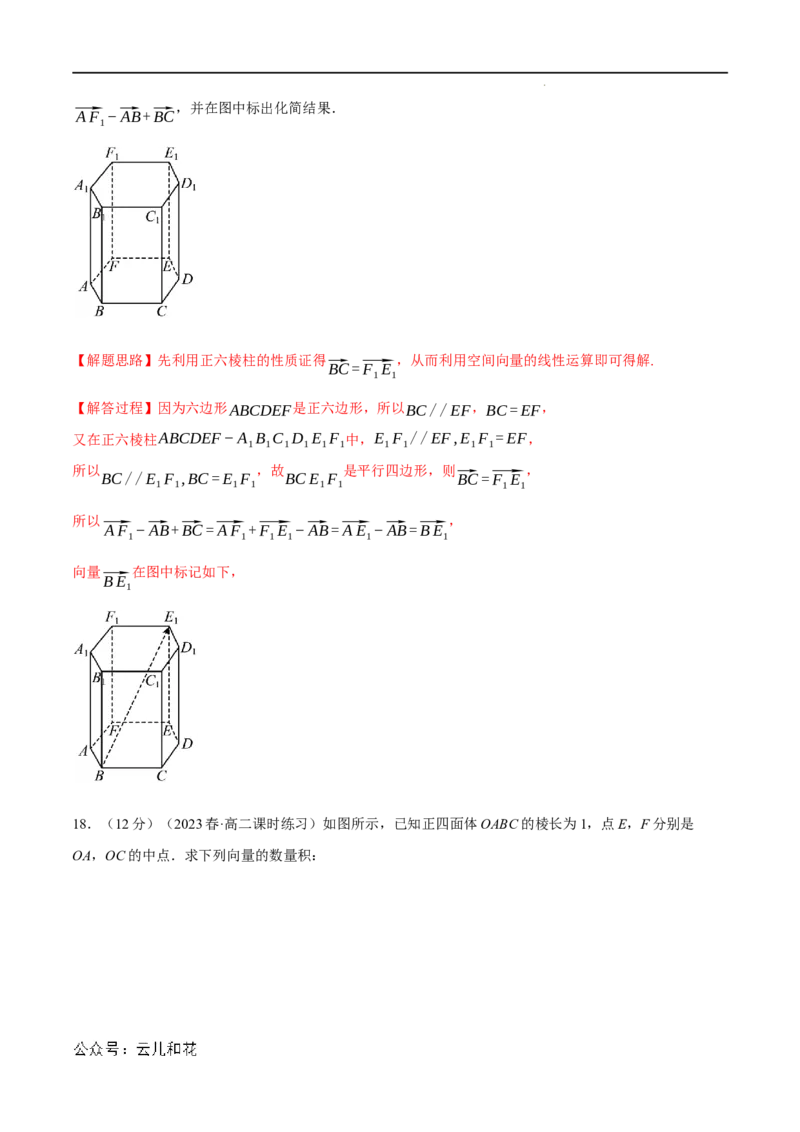
17.(10分)(2023秋·高二课时练习) 在正六棱柱ABCDEF−A B C D E F 中,化简
1 1 1 1 1 1
学科网(北京)股份有限公司,并在图中标出化简结果.
⃗AF −⃗AB+⃗BC
1
【解题思路】先利用正六棱柱的性质证得 ,从而利用空间向量的线性运算即可得解.
⃗BC=⃗F E
1 1
【解答过程】因为六边形ABCDEF是正六边形,所以BC//EF,BC=EF,
又在正六棱柱ABCDEF−A B C D E F 中,E F //EF,E F =EF,
1 1 1 1 1 1 1 1 1 1
所以 ,故 是平行四边形,则 ,
BC//E F ,BC=E F BCE F ⃗BC=⃗F E
1 1 1 1 1 1 1 1
所以 ,
⃗AF −⃗AB+⃗BC=⃗AF +⃗F E −⃗AB=⃗AE −⃗AB=⃗BE
1 1 1 1 1 1
向量 在图中标记如下,
⃗BE
1
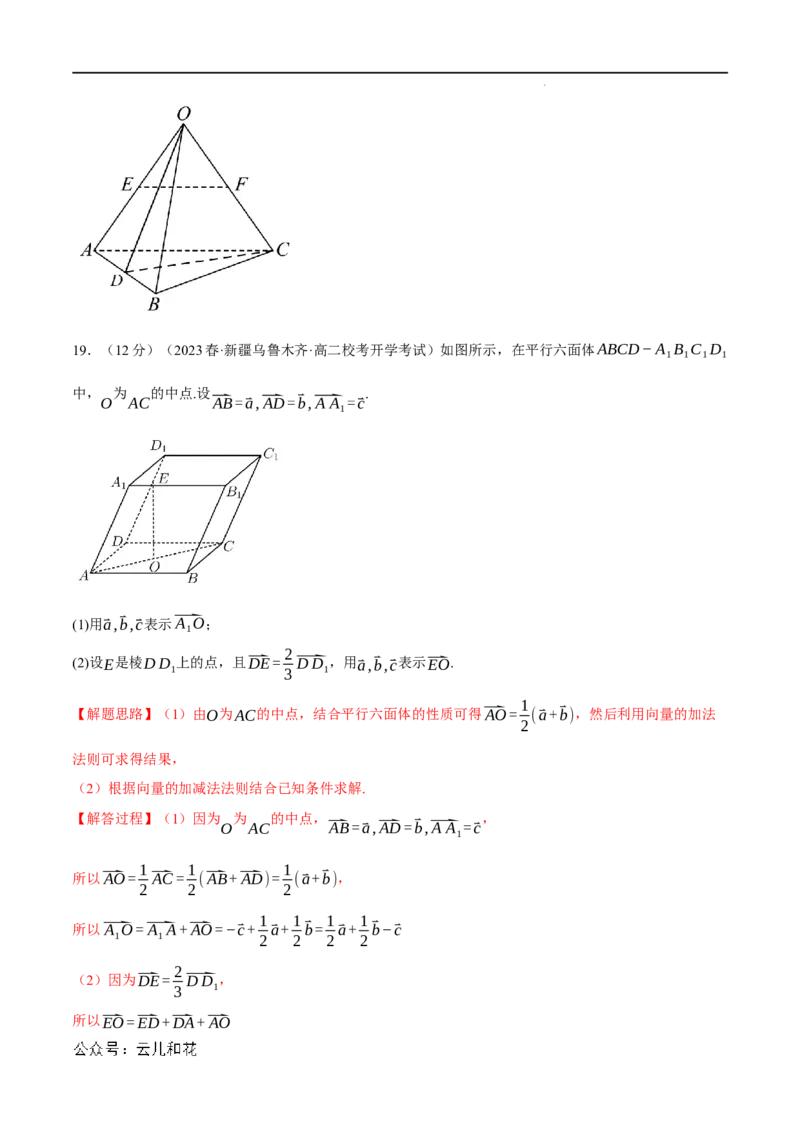
18.(12分)(2023春·高二课时练习)如图所示,已知正四面体OABC的棱长为1,点E,F分别是
OA,OC的中点.求下列向量的数量积:
学科网(北京)股份有限公司(1)⃗OA⋅⃗OB
(2)⃗EF⋅⃗CB
(3)
(⃗OA+⃗OB)⋅(⃗CA+⃗CB)
【解题思路】(1)正四面体的每个面均为等边三角形,夹角为60°,再结合空间向量数量积的运算法则,
得解;
1
(2)由⃗EF= ⃗AC,代入运算,即可得解;
2
(3)取AB的中点D,连接DO,DC,可推出(⃗OA+⃗OB)⋅(⃗CA+⃗CB)=4⃗OD⋅⃗CD,再在△OCD中,利
用余弦定理求出cos∠ODC的值,从而得解.
1
【解答过程】(1)⃗OA⋅⃗OB=|⃗OA|⋅|⃗OB|cos∠AOB=1×1×cos60°=
2
1 1 1
(2)⃗EF⋅⃗CB= ⃗AC⋅⃗CB= ×1×1×cos120°=− ;
2 2 4
(3)取AB的中点D,连接DO,DC,则⃗OA+⃗OB=2⃗OD,⃗CA+⃗CB=2⃗CD,
√3
在△OCD中,DO=DC= ,OC=1,
2
2 2
√3 √3
( ) +( ) −1
DO2+DC2−OC2 2 2 1
由余弦定理知,cos∠ODC= = = ,
2DO⋅DC √3 √3 3
2× ×
2 2
√3 √3 1
所以(⃗OA+⃗OB)⋅(⃗CA+⃗CB)=4⃗OD⋅⃗CD=4× × × =1.
2 2 3
学科网(北京)股份有限公司19.(12分)(2023春·新疆乌鲁木齐·高二校考开学考试)如图所示,在平行六面体ABCD−A B C D
1 1 1 1
中, 为 的中点.设 .
O AC ⃑AB=⃑a,⃑AD=⃑b,⃑A A =⃑c
1
(1)用⃑a,⃑b,⃑c表示⃑A O;
1
2
(2)设E是棱DD 上的点,且⃑DE= ⃑DD ,用 ⃑a,⃑b,⃑c表示⃑EO.
1 3 1
1
【解题思路】(1)由O为AC的中点,结合平行六面体的性质可得⃑AO= (⃑a+⃑b),然后利用向量的加法
2
法则可求得结果,
(2)根据向量的加减法法则结合已知条件求解.
【解答过程】(1)因为 为 的中点, ,
O AC ⃑AB=⃑a,⃑AD=⃑b,⃑A A =⃑c
1
1 1 1
所以⃑AO= ⃑AC= (⃑AB+⃑AD)= (⃑a+⃑b),
2 2 2
1 1 1 1
所以⃑A O=⃑A A+⃑AO=−⃑c+ ⃑a+ ⃑b= ⃑a+ ⃑b−⃑c
1 1 2 2 2 2
2
(2)因为⃑DE= ⃑DD ,
3 1
所以⃑EO=⃑ED+⃑DA+⃑AO
学科网(北京)股份有限公司2 1
=− ⃑DD −⃑AD+ (⃑a+⃑b)
3 1 2
2 1
=− ⃑c−⃑b+ (⃑a+⃑b)
3 2
1 1 2
= ⃑a− ⃑b− ⃑c.
2 2 3
20.(12分)(2023秋·湖南岳阳·高二统考期末)已知⃑a=(2,−1,−4),⃑b=(−1,k,2).
(1)若(⃑a−⃑b)//(⃑a+⃑b),求实数k的值;
(2)若(⃑a+3⃑b)⊥(⃑a+⃑b),求实数k的值.
【解题思路】(1)根据空间平行向量的性质,结合空间向量线性运算坐标表示公式进行求解即可;
(2)根据空间向量互相垂直的性质,结合空间向量线性运算坐标表示公式、数量积的坐标表示公式进行
求解即可;
【解答过程】(1)
⃑a−⃑b=(2,−1,−4)−(−1,k,2)=(3,−1−k,−6),⃑a+⃑b=(2,−1,−4)+(−1,k,2)=(1,k−1,−2),若
1
(⃑a−⃑b)∥(⃑a+⃑b),则 ⃑a−⃑b=λ(⃑a+⃑b),即3=λ,−1−k=λ(k−1),−6=−2λ,解得λ=3,k= ;
2
(2) ,若 ,则
⃑a+3⃑b=(2,−1,−4)+3(−1,k,2)=(−1,3k−1,2),⃑a+⃑b=(1,k−1,−2) (⃑a+3⃑b)⊥(⃑a+⃑b)
,即 ,化简可得 ,解得
(⃑a+3⃑b)⋅(⃑a+⃑b)=0 (−1)×1+(3k−1)×(k−1)+2×(−2)=0 3k2−4k−4=0 k=2
2
或k=− .
3
21.(12分)(2023·全国·高三专题练习)如图,在四棱锥P−ABCD中,PA⊥底面ABCD,AD⊥AB,
AB//DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.证明:
(1)BE⊥DC;
(2)BE//平面PAD;
(3)平面PCD⊥平面PAD.
【解题思路】(1)以点A为原点建立空间直角坐标系,写出点B,E,D,C的坐标,把⃑BE,⃑DC坐标写出,
学科网(北京)股份有限公司两向量作数量积为零,即可得到垂直;
(2)取PD的中点,设为F,连接EF,AF,证出四边形ABEF为平行四边形,即得出AF//BE,利用线
面平行的判定定理得到BE//平面PAD.
(3)利用PA⊥DC,DC⊥AD(线线垂直)推出DC⊥面PAD(线面垂直),由于DC⊂面PDC,再
由面面垂直的判定定理推出平面PCD⊥平面PAD.
【解答过程】(1)证明: 依题意,以点A为原点建立空间直角坐标系(如图),
∵AD=DC=AP=2,AB=1,可得B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2).由E为棱PC的中点,得
E(1,1,1).
(1)向量⃑BE=(0,1,1),⃑DC=(2,0,0),故⃑BE⋅⃑DC=0.
所以⃑BE⋅⃑DC=0.
1
(2)取PD的中点,设为F,连接EF,AF,∵E,F 分别是PD,PC的中点,∴EF//DC且EF= DC,
2
由题意知AB//DC,DC=2AB=2,∴EF//AB且EF=AB,即四边形ABEF为平行四边形,即
AF//BE,∵AF⊂面APD,BE⊄面PAD,∴BE//平面PAD.
(3)∵PA⊥底面ABCD,DC⊂底面ABCD,∴PA⊥DC,∵AD⊥AB,AB//DC,∴DC⊥AD,
PA,AD⊂面PAD,PA∩AD=A,∴DC⊥面PAD,∵DC⊂面PDC,∴ 平面PCD⊥平面PAD.
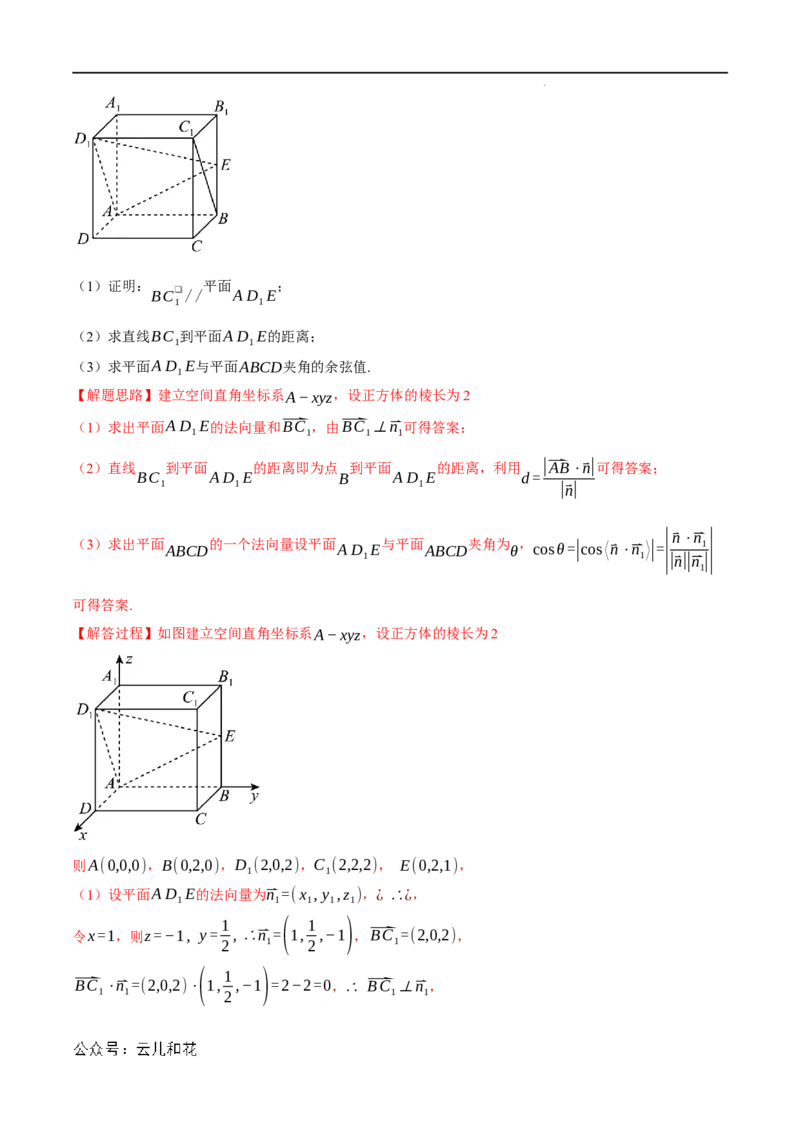
22.(12分)(2023·全国·高三专题练习)如图,在正方体ABCD−A B C D 中,E为BB 的中点.
1 1 1 1 1
学科网(北京)股份有限公司(1)证明: 平面 ;
BC❑// AD E
1 1
(2)求直线BC 到平面AD E的距离;
1 1
(3)求平面AD E与平面ABCD夹角的余弦值.
1
【解题思路】建立空间直角坐标系A−xyz,设正方体的棱长为2
(1)求出平面AD E的法向量和⃑BC ,由⃑BC ⊥⃑n 可得答案;
1 1 1 1
(2)直线 到平面 的距离即为点 到平面 的距离,利用 |⃑AB⋅⃑n|可得答案;
BC AD E B AD E d=
1 1 1
|⃑n|
|⃑n⋅⃑n |
(3)求出平面 ABCD 的一个法向量设平面 AD E 与平面 ABCD 夹角为 θ , cosθ=|cos⟨⃑n⋅⃑n ⟩|= 1
1 1 |⃑n||⃑n|
1
可得答案.
【解答过程】如图建立空间直角坐标系A−xyz,设正方体的棱长为2
则A(0,0,0),B(0,2,0),D (2,0,2),C (2,2,2), E(0,2,1),
1 1
(1)设平面AD E的法向量为⃑n =(x ,y ,z ),¿ ∴¿,
1 1 1 1 1
1 ( 1 )
令x=1,则z=−1, y= , ∴⃑n = 1, ,−1 ,⃑BC =(2,0,2),
2 1 2 1
( 1 )
⃑BC ⋅⃑n =(2,0,2)⋅ 1, ,−1 =2−2=0,∴ ⃑BC ⊥⃑n ,
1 1 2 1 1
学科网(北京)股份有限公司∵ C B⊄面AD E ∴BC //平面AD E.
1 1 1 1
(2)∵BC //平面AD E,直线BC 到平面AD E的距离即为点B到平面AD E的距离,
1 1 1 1 1
| 1 |
0×1+2× +0×(−1)
⃑AB=(0,2,0) , ⃑n = ( 1, 1 ,−1 ), d= |⃑AB⋅⃑n 1 | = 2 =2,
1 2 |⃑n| √ 1 3
1 1+1+
4
2
∴直线BC 到平面AD E的距离为 .
1 1 3
(3)平面ABCD的一个法向量为⃑n=(0,0,2),设平面AD E与平面ABCD夹角为θ,
1
1
| 0×1+0× +2×(−1) |
⃑n = ( 1, 1 ,−1 ), cosθ=|cos⟨⃑n⋅⃑n ⟩|= |⃑n⋅⃑n 1 | = 2 =2,
1 2 1 |⃑n||⃑n| √ 1 3
1 2 1+1+
4
2
所以平面AD E与平面ABCD夹角的余弦值 .
1 3
学科网(北京)股份有限公司