文档内容
第一章 空间向量与立体几何全章综合测试卷(提高篇)
【人教A版(2019)】
考试时间:120分钟;满分:150分
姓名:___________班级:___________考号:___________
考卷信息:
本卷试题共22题,单选8题,多选4题,填空4题,解答6题,满分150分,限时120分钟,本卷题型针对性
较高,覆盖面广,选题有深度,可衡量学生掌握本章内容的具体情况!
一.选择题(共8小题,满分40分,每小题5分)
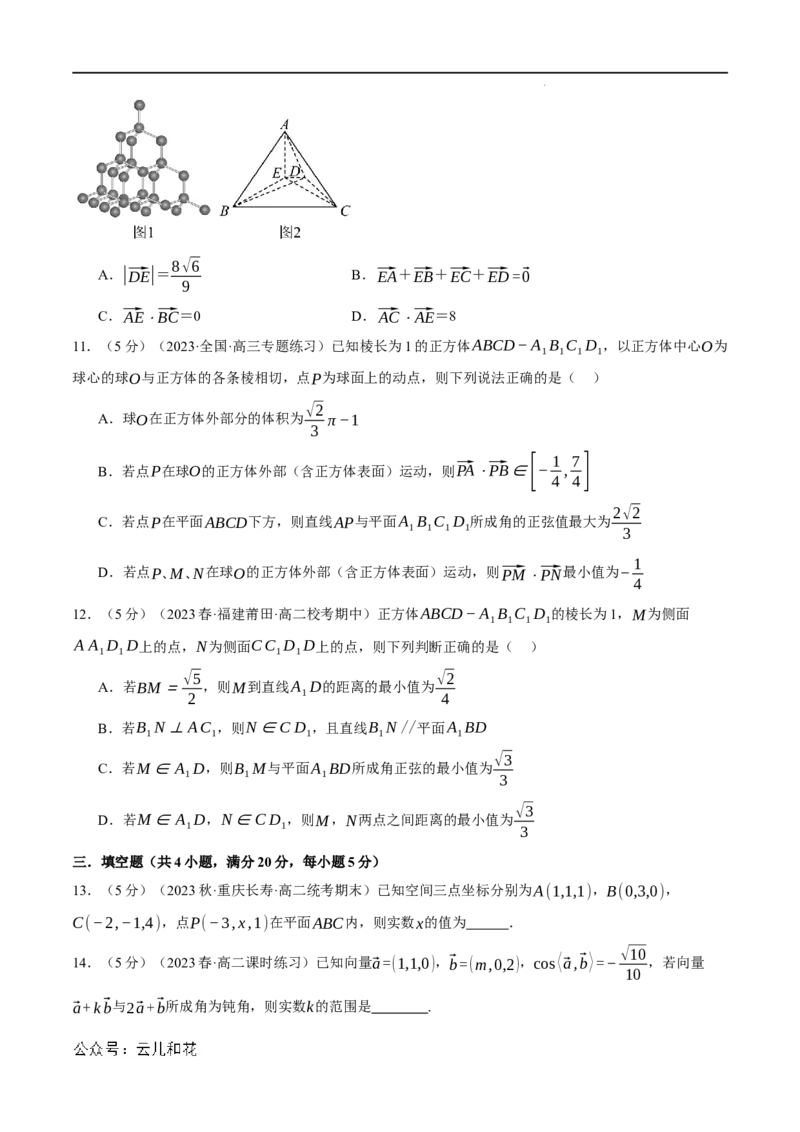
1.(5分)(2023秋·河北保定·高二统考期末)在以下命题中:
①三个非零向量⃗a,⃗b,⃗c不能构成空间的一个基底,则⃗a,⃗b,⃗c共面;
②若两个非零向量⃗a,⃗b与任何一个向量都不能构成空间的一个基底,则⃗a,⃗b共线;
③对空间任意一点O和不共线的三点A,B,C,若⃗OP=2⃗OA−⃗2OB−⃗2OC,则P,A,B,C四点共面
④若 , 是两个不共线的向量,且 ,则 构成空间的一个基底
⃗a ⃗b ⃗c=λ⃗a+μ⃗b(λ,μ∈R,λ,μ≠0) {⃗a,⃗b,⃗c}
⑤若 为空间的一个基底,则 构成空间的另一个基底;其中真命题的个数是
{⃗a,⃗b,⃗c} {⃗a+⃗b,⃗b+⃗c+2⃗a,⃗c+⃗a}
( )
A.0 B.1 C.2 D.3
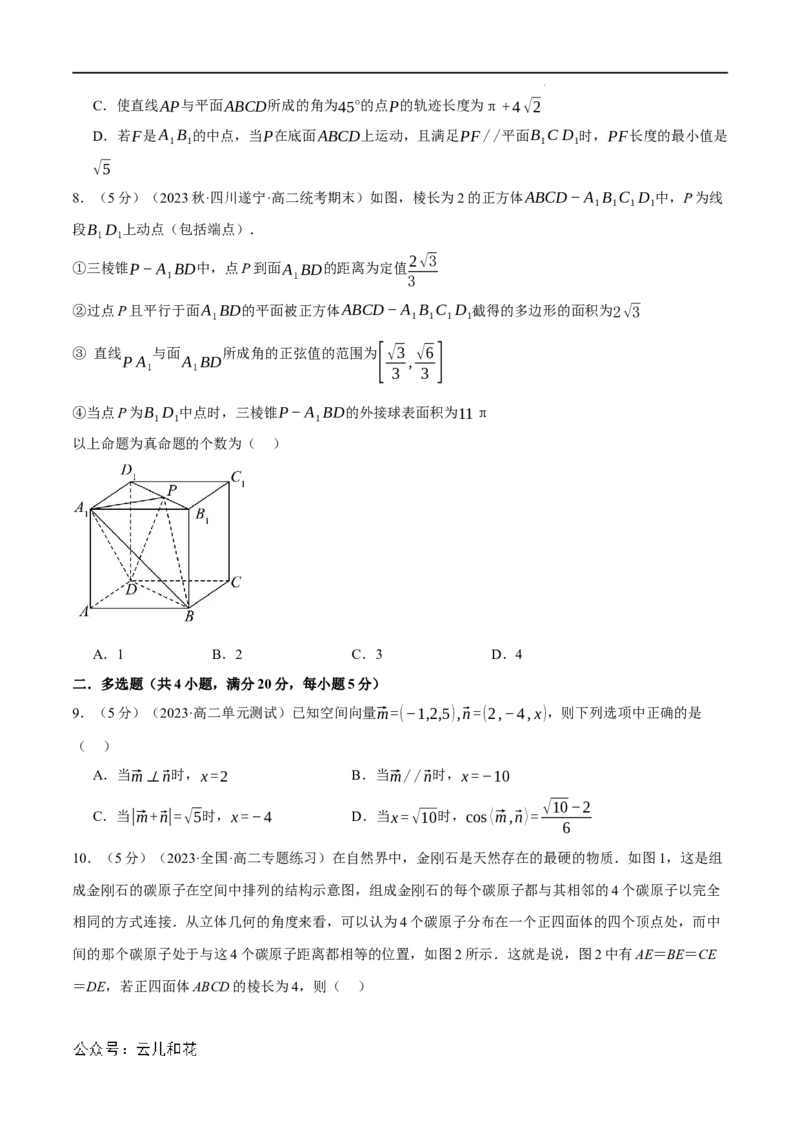
2.(5分)(2023·全国·高三专题练习)已知MN是棱长为4的正方体内切球的一条直径,点P在正方体
表面上运动,则⃑PM⋅⃑PN的最大值为( )
A.4 B.12 C.8 D.6
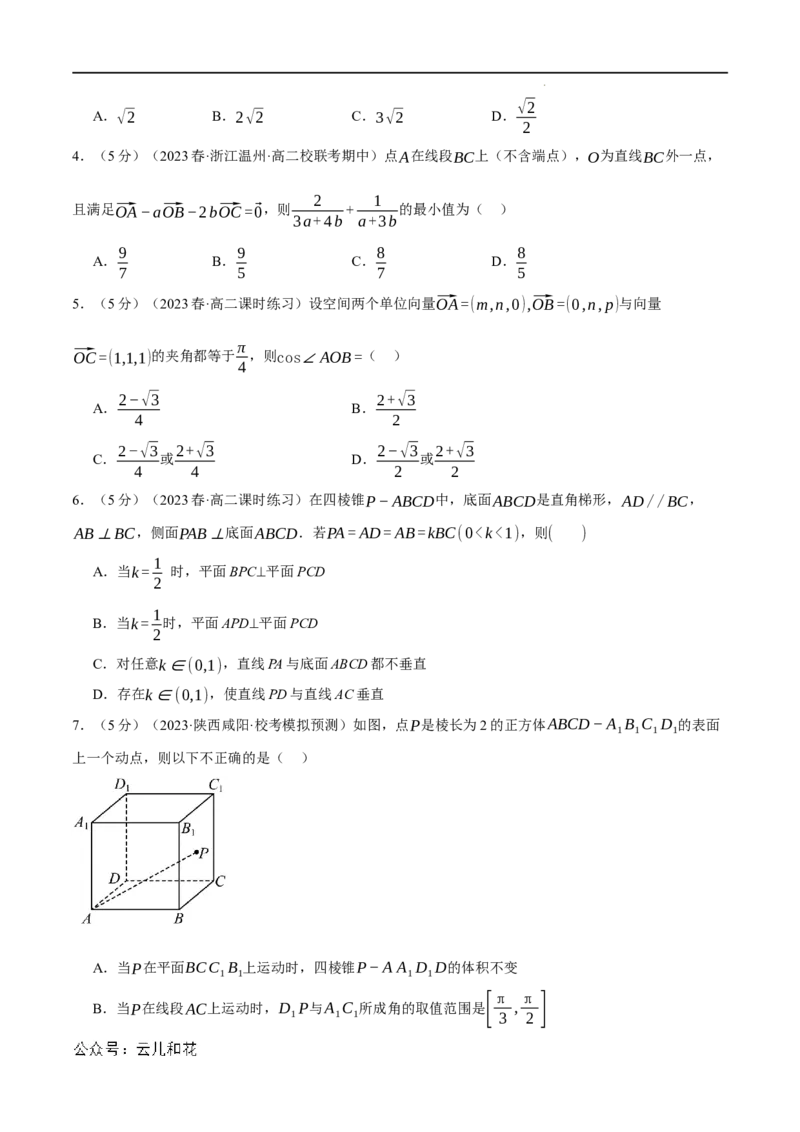
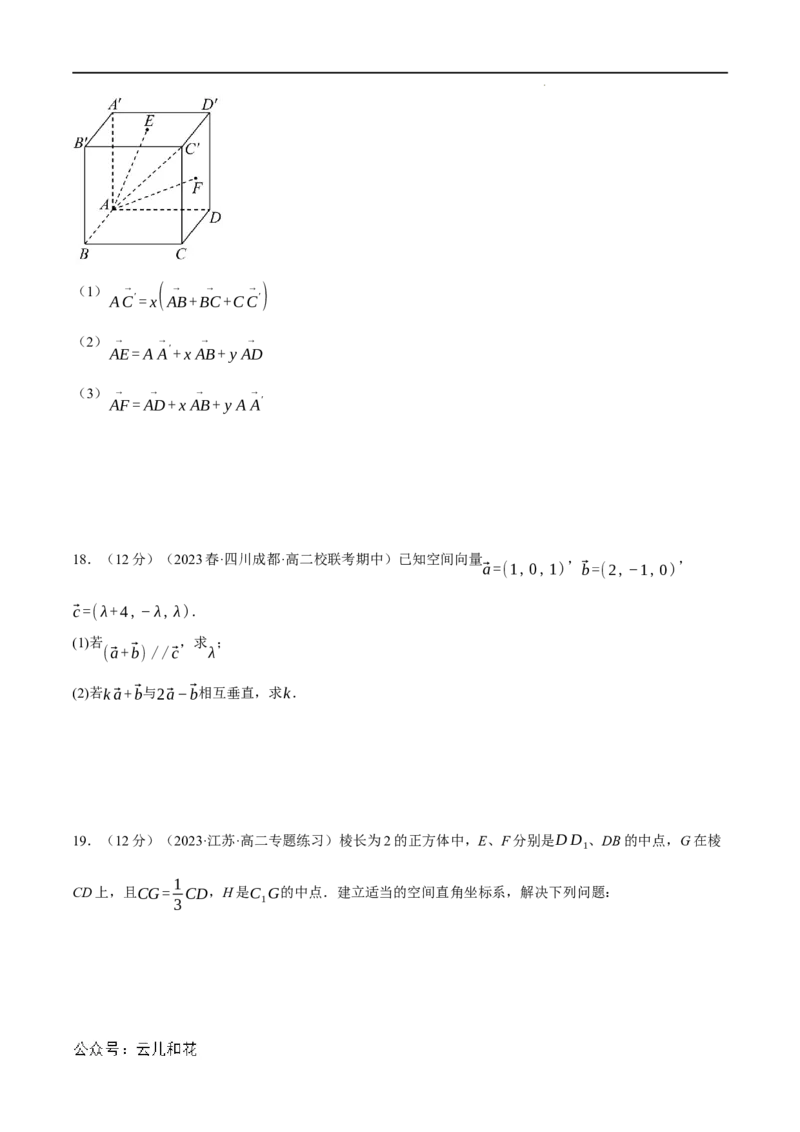
3.(5分)(2023春·江苏徐州·高二统考期中)在如图所示的试验装置中,两个正方形框架ABCD,ABEF
的边长都是2,且它们所在的平面互相垂直,活动弹子M,N分别在正方形对角线AC和BF上移动,且
CM和BN的长度保持相等,记CM=BN=a,其中0;
1
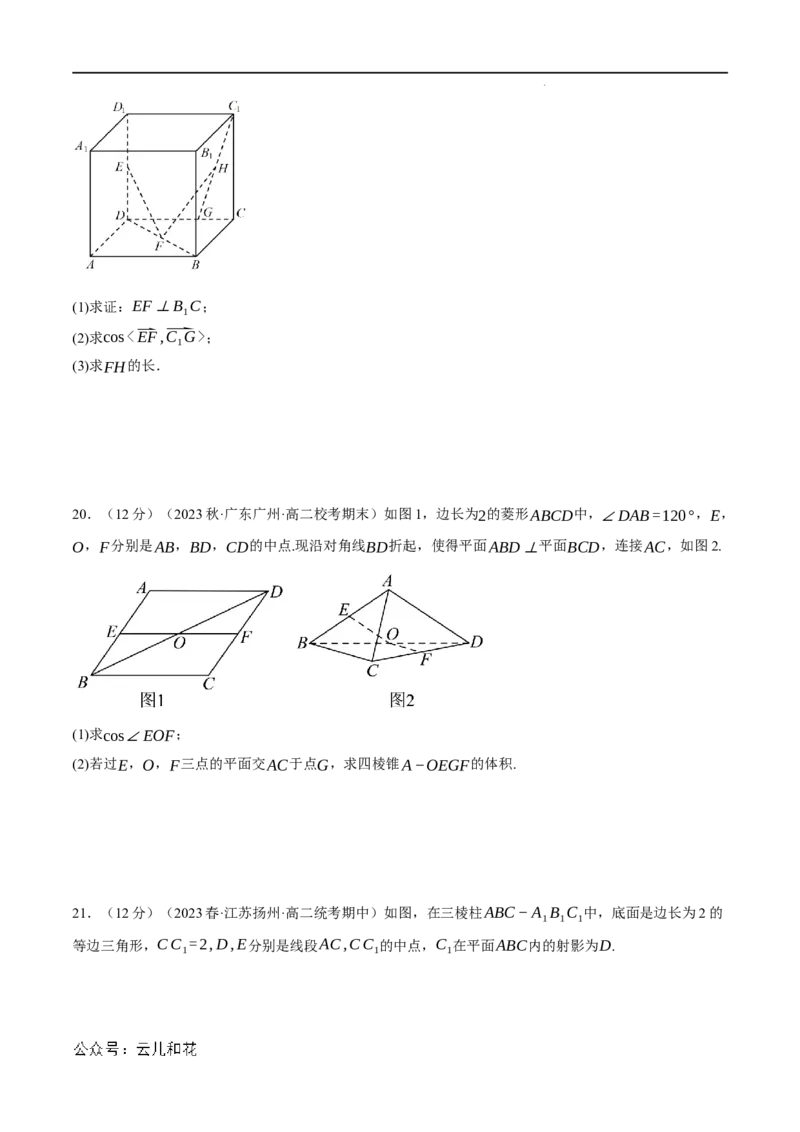
(3)求FH的长.
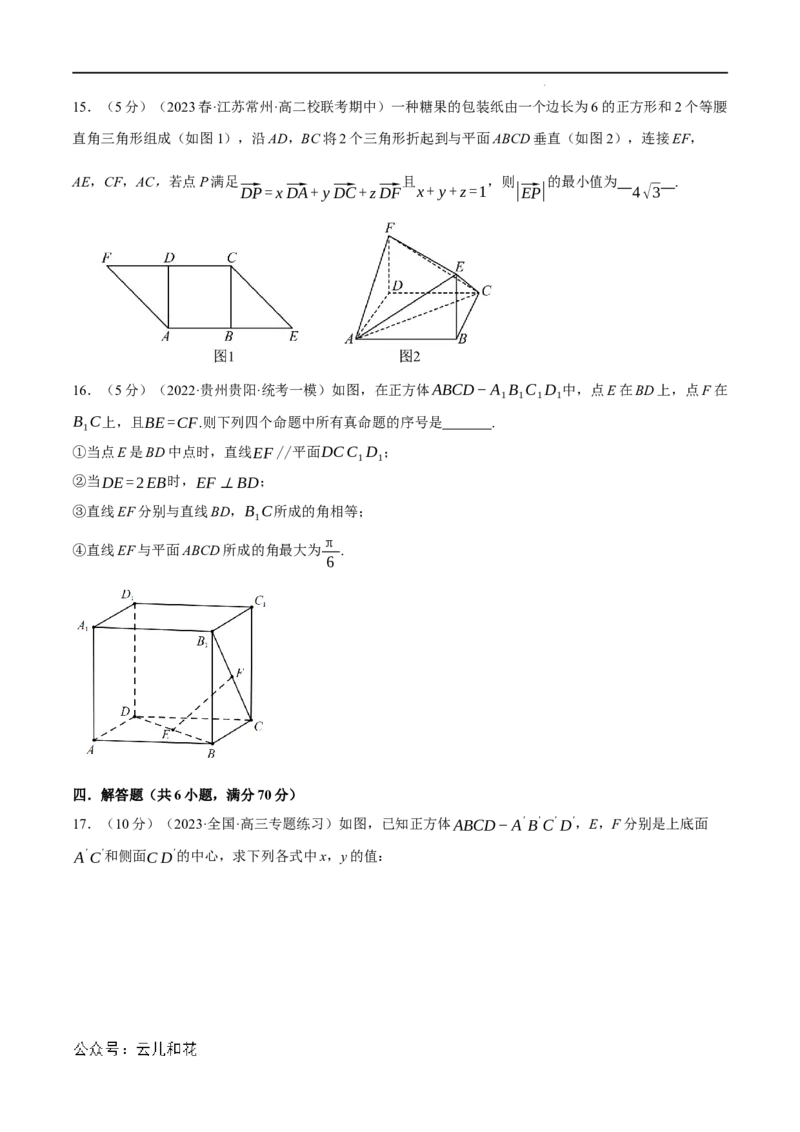
20.(12分)(2023秋·广东广州·高二校考期末)如图1,边长为2的菱形ABCD中,∠DAB=120°,E,
O,F分别是AB,BD,CD的中点.现沿对角线BD折起,使得平面ABD⊥平面BCD,连接AC,如图2.
(1)求cos∠EOF;
(2)若过E,O,F三点的平面交AC于点G,求四棱锥A−OEGF的体积.
21.(12分)(2023春·江苏扬州·高二统考期中)如图,在三棱柱ABC−A B C 中,底面是边长为2的
1 1 1
等边三角形,CC =2,D,E分别是线段AC,CC 的中点,C 在平面ABC内的射影为D.
1 1 1
学科网(北京)股份有限公司(1)求证:A C⊥平面BDE;
1
(2)若点F为棱B C 的中点,求点F到平面BDE的距离;
1 1
(3)若点F为线段B C 上的动点(不包括端点),求锐二面角F−BD−E的余弦值的取值范围.
1 1
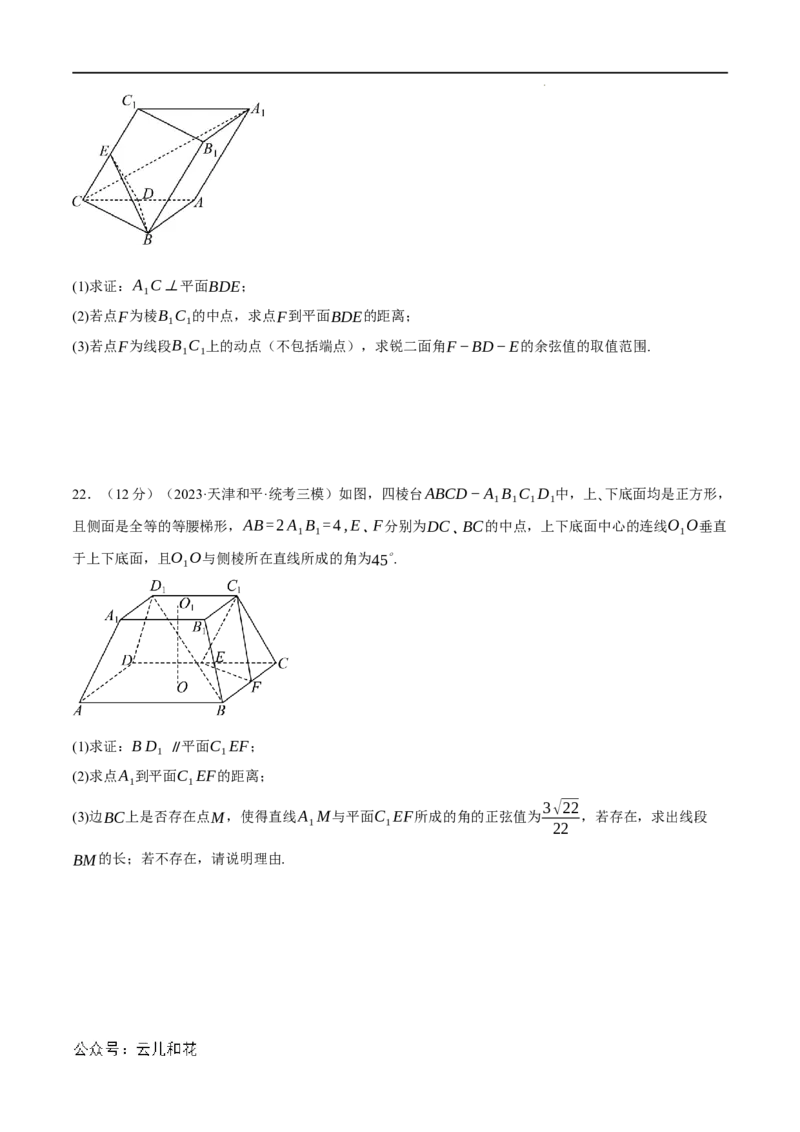
22.(12分)(2023·天津和平·统考三模)如图,四棱台ABCD−A B C D 中,上、下底面均是正方形,
1 1 1 1
且侧面是全等的等腰梯形,AB=2A B =4,E、F分别为DC、BC的中点,上下底面中心的连线O O垂直
1 1 1
于上下底面,且O O与侧棱所在直线所成的角为45∘.
1
(1)求证:BD ∥平面C EF;
1 1
(2)求点A 到平面C EF的距离;
1 1
3√22
(3)边BC上是否存在点M,使得直线A M与平面C EF所成的角的正弦值为 ,若存在,求出线段
1 1 22
BM的长;若不存在,请说明理由.
学科网(北京)股份有限公司