文档内容
2025-2026 学年内蒙古自治区鄂尔多斯市第一中学高二上学期 12 月月
考数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若方程x2+ y2−2x−m=0表示圆,则m的范围是( )
A. (−∞,−1) B. [−1,+∞) C. (−1,+∞) D. (−∞,−1]
2.已知圆 截直线 所得线段的长度是 ,则圆 与圆
M:x2+ y2+2ax=0(a>0) x+ y=0 2√2 M
的位置关系是( )
N:(x+6) 2+(y−3) 2=9
A. 内切 B. 相交 C. 外切 D. 相离
3.直线l :y=x+a和l :y=x+b将单位圆C:x2+ y2=2分成长度相等的四段弧,则a2+b2=( )
1 2
A. √2 B. 2 C. 3 D. 4
4.已知椭圆 x2 的右焦点为 ,点 在 上,点 到直线 4√3的距离为√3,则
C: + y2=1(a>0) F(√3,0) P C P x=
a2 3 3
|PF|=( )
1 1 √3
A. B. C. D. 1
3 2 2
5.若圆 与圆 外切,则 ( )
C :x2+ y2=1 C :x2+ y2−6x−8 y+m=0 m=
1 2
A. 9 B. 11 C. 19 D. 21
6.已知圆 和两点 ,若圆 上存在点 ,使得
C:(x−4) 2+(y+3) 2=4 A(−a,0),B(a,0)(a>0) C P
∠APB=90°,则a的最大值为( )
A. 3 B. 5 C. 7 D. 9
7.若双曲线经过点 ,且它的两条渐近线方程是 ,则双曲线的离心率是( )
(−√3,6) y=±3x
10 √10
A. B. 10 C. D. √10
3 3
8.若{
e
⃗
,e
⃗
,e
⃗}是空间向量中的一个基底,那么对任意一个空间向量 ⃗a,存在唯一的有序实数组 (x,y,z) ,
1 2 3
第 页,共 页
1 1使得⃗
a=xe
⃗
+ ye
⃗
+ze
⃗,我们把有序实数组(x,y,z)叫做基底{
e
⃗
,e
⃗
,e
⃗}下向量⃗a的斜坐标.设向量⃗p在
1 2 3 1 2 3
基底{⃗
a,
⃗
b,
⃗
c
}下的斜坐标为 {−1,2,3} ,则向量 ⃗p 在基底{⃗
a+
⃗
b,
⃗
a−
⃗
b,
⃗
c
}下的斜坐标为( )
1 3 1 3 1 3 1 3
A. ( ,− ,3) B. (− ,− ,3) C. (− , ,3) D. ( ,− ,−3)
2 2 2 2 2 2 2 2
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知i⃗,⃗j,⃗k是空间中三个向量,则下列说法错误的是( )
A. 对于空间中的任意一个向量 ,总存在实数 ,使得⃗ ⃗ ⃗ ⃗
⃗m x,y,z
m=xi+ y j+zk
B. 若{⃗ ⃗ ⃗}是空间的一个基底,则{⃗ ⃗ ⃗ ⃗ ⃗ ⃗}也是空间的一个基底
i, j,k i−3 j, j+k,k−2i
C. 若⃗ ⃗,⃗ ⃗,则⃗ ⃗
i⊥j k⊥j i//k
D. 若i⃗,⃗j,⃗k所在直线两两共面,则i⃗,⃗j,⃗k共面
10.下列说法不正确的是( )
A. 任意一条直线都有倾斜角,但不一定有斜率
B. 点(0,1)关于直线y=x的对称点为(1,1)
C. 直线x−y−3=0与两坐标轴围成的三角形的面积是2
D. 经过点(1,1)且在x轴和y轴上截距都相等的直线方程为x+ y−2=0
11.下列说法正确的是( )
A. 若abc≠0,且直线ax+by+c=0不经过第二象限,则ab>0,bc<0
B. 方程(2+λ)x+(1−2λ)y−5=0(λ∈R)表示的直线都经过点(2,1)
C. m∈R,直线m2x+ y+2=0不可能与y轴垂直
D. 直线3x+3 y−1=0的横、纵截距相等
三、填空题:本题共3小题,每小题5分,共15分。
12.抛物线 上一点 的横坐标为 ,且 ,则抛物线方程为 .
y2=2px(p>0) M 3 |MF|=2p
13.已知直线l :x+2my−1=0与l :(3m−1)x−my−1=0平行,则实数m= .
1 2
x2 y2
14.已知方程 + =1表示双曲线,则实数m的取值范围为 .
m−2 2m−3
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
第 页,共 页
2 115.(本小题13分)
已知圆 是圆 内一点, 是圆 外一点.
O:x2+ y2=8,M(−1,2) O P(4,0) O
(1)AB是圆O中过点M最长的弦,CD是圆O中过点M最短的弦,求四边形ACBD的面积;
(2)过点P作直线l交圆于E、F两点,求▵OEF面积的最大值,并求此时直线l的方程.
16.(本小题15分)
已知点A(2,4),直线l:x−2y+1=0,且点M,N均在直线l上,AM⊥l,
(1)求点M的坐标:
(2)若|MN|=√5,求直线AN的方程.
17.(本小题15分)
已知椭圆 :x2 y2 的离心率为√5,上、下顶点分别为 , ,右顶点为 ,且 的面
E + =1(a>b>0) A B C ▵ABC
a2 b2 3
积为6.
(1)求E的方程;
(2)若点P为E上异于顶点的一点,直线是AP与BC交于点M,直线CP交y轴于点N,试判断直线MN是
否过定点?若是,则求出该定点坐标;若不是,请说明理由.
18.(本小题17分)
已知P是矩形ABCD所在平面外一点,M,N分别是AB,PC的中点,设⃗PA=⃗a,⃗PB=⃗b,⃗PC=⃗c,
(1) 以{⃗ ⃗ ⃗}为空间基底表示向量⃗MN .
a,b,c
(2)求证:MN//平面PAD.
19.(本小题17分)
如图,在正三棱柱 中, , , 分别为 , , 的中点, , .
A B C −ABC D E F AC CC BC A A=2√3 AB=2
1 1 1 1 1
第 页,共 页
3 1(1)证明: 平面A B E.
1 1
(2)若B F⊥平面α,求平面α与平面A B E夹角的余弦值.
1 1 1
第 页,共 页
4 1参考答案
1.C
2.C
3.D
4.B
5.A
6.C
7.C
8.A
9.ACD
10.BCD
11.BD
12.y2=4x
1
13.0或 .
6
14.(3 )
,2
2
15.【详解】(1)M(−1,2)在圆x2+ y2=8内,由于圆内弦最长的即是圆的直径即AB为直径,
而CD是过M且与AB垂直的弦
此时 ,圆心 到直线 的距离 ,
AB=4√2 (0,0) CD d=√12+22=√5
从而可得,CD=2√3,
1
∴S= ×2√3×4√2=4√6;
2
1
(2)|OE|=|OF|=2√2,S = ×|OE|×|OF|×sin∠EOF,
▵OEF 2
π
当∠EOF= 时,▵OEF面积的最大值为4,
2
此时,O到直线l的距离为2,|OP|=4,
π 5π
∴直线l的倾斜角为 或 ,
6 6
√3
则直线l的斜率为± ,
3
第 页,共 页
5 1√3
∴直线l的方程为y=± (x−4).
3
{
m−2n+1=0
16.【详解】 设 ,由题意可得: ,解得:{m=3
(1) M(m,n) n−4 1 ,
× =−1 n=2
m−2 2
所以点M的坐标为(3,2).
(2)设N(s,t),由(1)知点M的坐标为(3,2).
根据题意可得{ s−2t+1=0 ,解得{s=5或{s=1
,
√(s−3) 2+(t−2) 2=√5 t=3 t=1
所以点N的坐标为(5,3)或(1,1),
3−4
当点N为(5,3)时,直线AN的方程为y−3= (x−5),即x+3 y−14=0,
5−2
1−4
当点N为(1,1)时,直线AN的方程为y−1= (x−1),即3x−y−2=0,
1−2
综上所述:直线AN的方程为3x−y−2=0或x+3 y−14=0.
c √5
{ = ,
a 3
17.【详解】 由题意知 解得 , , ,
(1) 1 a=3 b=2 c=√5
a⋅2b=6,
2
c2=a2−b2,
x2 y2
所以E的方程为 + =1.
9 4
(2)显然直线AP的斜率存在,设直线AP的斜率为k,则直线AP的方程为y=kx+2,
{
y=kx+2
又直线 的方程为 2 ,由 ,解得 12 , 6k+4,
BC y= x−2 2 x=− y=−
3 y= x−2 3k−2 3k−2
3
即 ( 12 6k+4).
M − ,−
3k−2 3k−2
第 页,共 页
6 1{x2 y2
由 + =1,得 ,解得 或 36k ,
9 4 (4+9k2)x2+36kx=0 x=0 x=−
4+9k2
y=kx+2
当 x=− 36k 时, y=k ( − 36k ) +2= 8−18k2 ,即 P ( − 36k , 8−18k2 ),
4+9k2 4+9k2 4+9k2 4+9k2 4+9k2
8−18k2
−0
所以直线 的斜率 4+9k2 6k−4,
CP k = =
CP 36k 9k+6
− −3
4+9k2
所以直线 的方程为 6k−4 ,令 ,得 4−6k,即 ( 4−6k).
CP y= (x−3) x=0 y= N 0,
9k+6 3k+2 3k+2
6k+4 4−6k
− −
3k−3 3k+2 4k
所以直线MN的斜率k = = ,
MN 12 3k+2
− −0
3k−3
4k 4−6k
所以直线MN的方程为y= x+ ,
3k+2 3k+2
4k
即y= (x−3)+2,所以直线MN过定点(3,2).
3k+2
⃗ ⃗ ⃗ 1 ⃗ 1( ⃗ ⃗ ) 1⃗ 1⃗ 1⃗
18.【详解】(1)MN=PN−PM= PC− PA+PB =− a− b+ c;
2 2 2 2 2
(2)取DC中点H,连接HM,HN,
第 页,共 页
7 1因为H是DC中点,N是PC中点,所以HN//DP,
因为HN⊄平面PAD,DP⊂平面PAD,
所以HN//平面PAD,
同理,得HM//DA,HM⊄平面PAD,DA⊂平面PAD,
所以HM//平面PAD,
又HN∩HM=H,HN⊂平面HNM,HM⊂平面HNM,
故平面HNM//平面PAD,
因为MN⊂平面HNM,
所以MN//平面PAD.
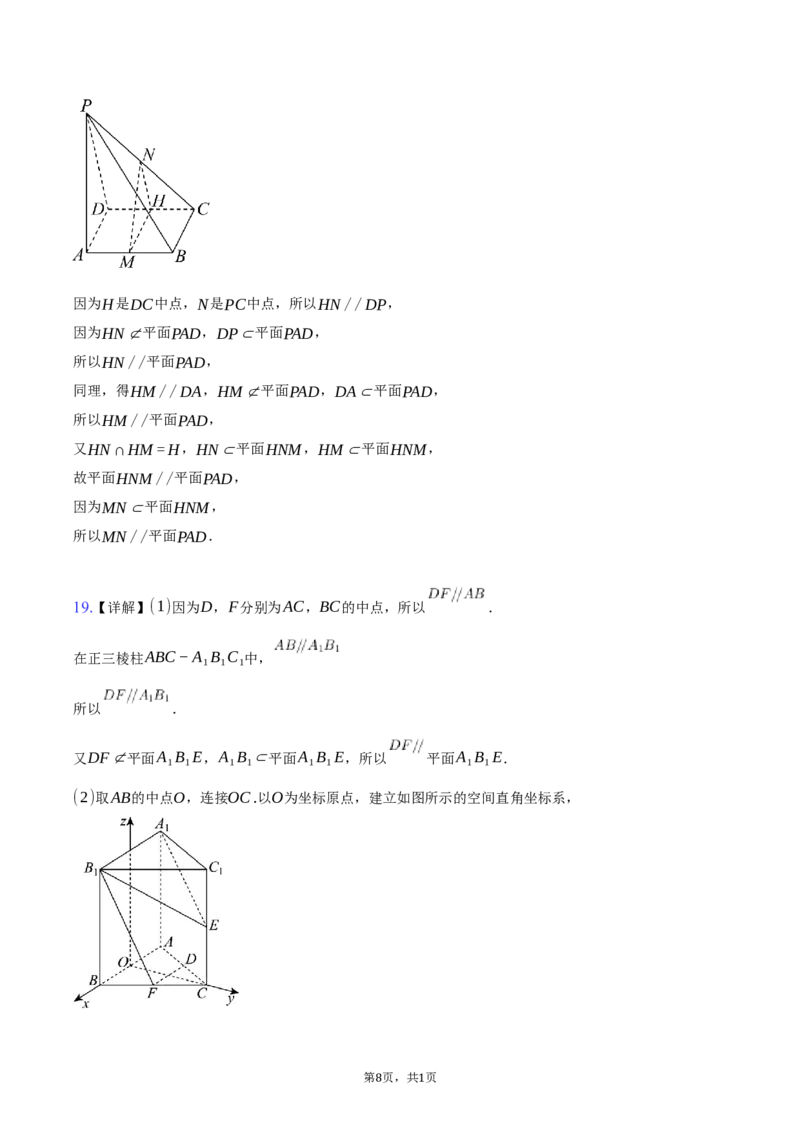
19.【详解】(1)因为D,F分别为AC,BC的中点,所以 .
在正三棱柱ABC−A B C 中,
1 1 1
所以 .
又DF⊄平面A B E,A B ⊂平面A B E,所以 平面A B E.
1 1 1 1 1 1 1 1
(2)取AB的中点O,连接OC.以O为坐标原点,建立如图所示的空间直角坐标系,
第 页,共 页
8 1则 , , , (1 √3 )
A (−1,0,2√3) B (1,0,2√3) E(0,√3,√3) F , ,0
1 1 2 2
⃗ , ⃗ .
A E=(1,√3,−√3) A B =(2,0,0)
1 1 1
设平面A B E的法向量为⃗n=(x,y,z),
1 1
{ ⃗ ⃗
n⋅A B =2x=0,
则 1 1
⃗ ⃗
n⋅A E=x+√3 y−√3z=0,
1
取y=1,则⃗n=(0,1,1)
易知 ⃗ ( 1 √3 )是平面 的一个法向量,
B F= − , ,−2√3 α
1 2 2
3√3
|⃗ ⃗ |
| ⟨⃗ ⃗ ⟩| n⋅B F 2 3√78
所以 cos n,B F = 1 = = .
1 |⃗|| ⃗ | √26 52
n B F
1
3√78
故平面α与平面A B E夹角的余弦值为 .
1 1 52
第 页,共 页
9 1