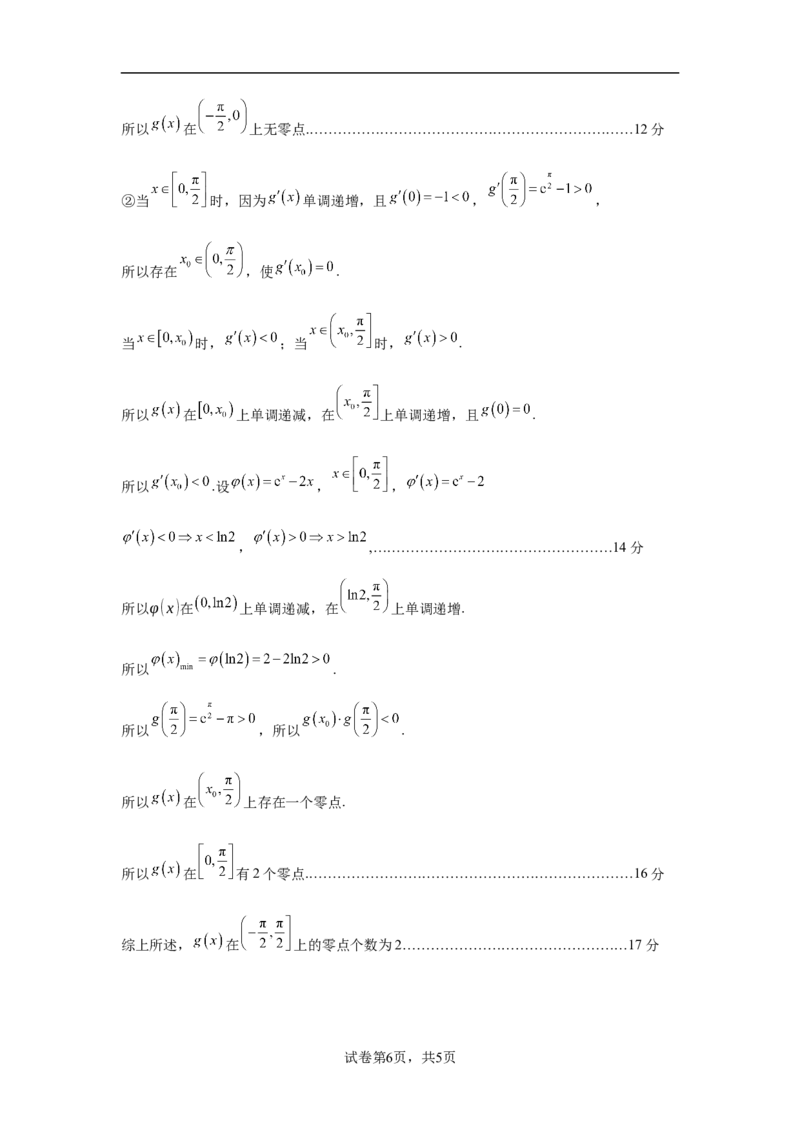文档内容
2025 年 1 月“八省联考”考前猜想卷
参考答案
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一
项是符合题目要求的。
1 2 3 4 5 6 7 8
D B C A D D C A
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9 10 11
ACD BD ABD
三、填空题:本题共3小题,每小题5分,共15分。
12.-1
13.
14.
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步棸。
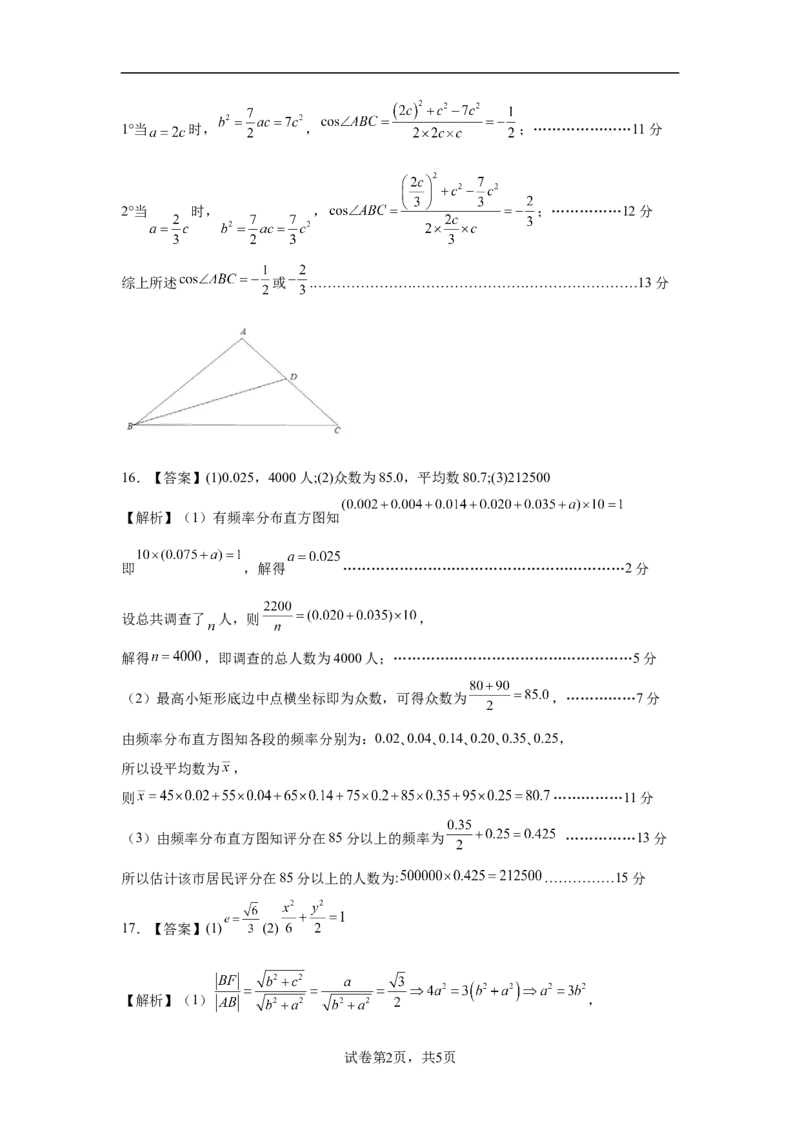
15.(13分【答案】(1)证明见解析;(2) 或
【解析】(1)点 在边 上,且满足 ,
所以 ,……………………………………………………3分
,……………………………………………………………4分
故 ,即 ;……………………………………………………………6分
(2)由图可知 ,
……………7分
可得 ,解得 或 ,……………9分
试卷第1页,共5页
学科网(北京)股份有限公司1°当 时, , ;…………………11分
2°当 时, , ;……………12分
综上所述 或 .……………………………………………………………13分
16.【答案】(1)0.025,4000人;(2)众数为85.0,平均数80.7;(3)212500
【解析】(1)有频率分布直方图知
即 ,解得 ……………………………………………………2分
设总共调查了 人,则 ,
解得 ,即调查的总人数为4000人;……………………………………………5分
(2)最高小矩形底边中点横坐标即为众数,可得众数为 ,……………7分
由频率分布直方图知各段的频率分别为:0.02、0.04、0.14、0.20、0.35、0.25,
所以设平均数为 ,
则 ……………11分
(3)由频率分布直方图知评分在85分以上的频率为 ……………13分
所以估计该市居民评分在85分以上的人数为: ……………15分
17.【答案】(1) (2)
【解析】(1) ,
试卷第2页,共5页离心率为 .…………………………………………………………5分
(2)由(1)可知椭圆的方程为 ,
易知直线 的斜率存在,设直线 的方程为 ,…………………………………6分
联立 得 ,………………………………8分
由 ,①………………………9分
, ,…………………………………………………11分
由 可得 ,②…………………………………………………12分
由 可得 ,③…………………………………………………13分
联立①②③可得 , , ,故椭圆的标准方程为 .………15分
18.【答案】(1)见解析;(2)
【解析】(1)由四边形 是直角梯形, , , ,
可得 , ,从而 是等边三角形, , 平分 .
为 的中点, , ,…………………………………3分
又 , , 平面 , 平面 ………………4分
平面 ,……………………………………………………………………5分
平面 ,所以平面 平面 .…………………………………6分
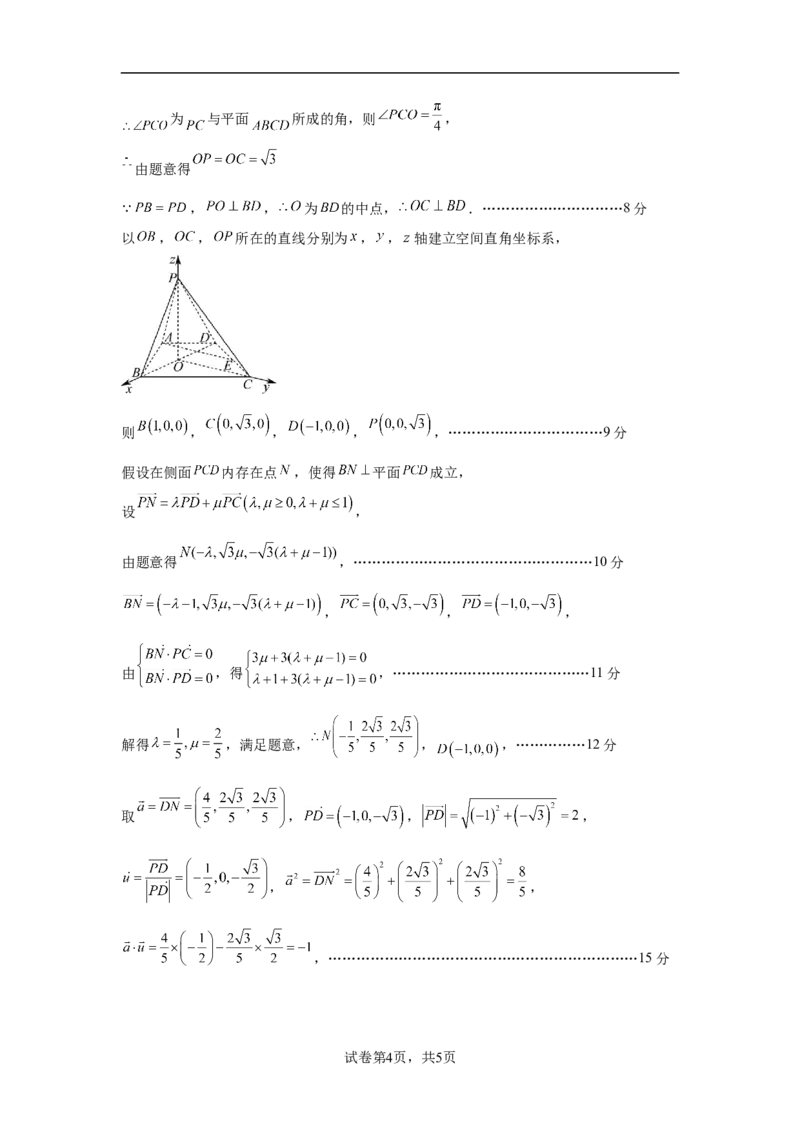
(2)在平面 内作 于 ,连接 , 平面 ,
又 平面 , 平面 平面 .
因为平面 平面 , 平面 , 平面
试卷第3页,共5页
学科网(北京)股份有限公司为 与平面 所成的角,则 ,
由题意得
, , 为 的中点, .…………………………8分
以 , , 所在的直线分别为 , , 轴建立空间直角坐标系,
则 , , , ,……………………………9分
假设在侧面 内存在点 ,使得 平面 成立,
设 ,
由题意得 ,……………………………………………10分
, , ,
由 ,得 ,……………………………………11分
解得 ,满足题意, , ,……………12分
取 , , ,
, ,
,…………………………………………………………15分
试卷第4页,共5页求出点N到直线PD的距离为: .…………………………16分
所以N点直线PD的距离为 .…………………………………………………………17分
19.【答案】(1) ;(2)1;(3)零点个数为2,证明见解析
【解析】(1)因为 ,所以 , ,………………1分
所以 ,………………………………………………3分
.………………………………………………………………5分
(2)由 , ,则 ,………………………6分
,令 ,则 ,故 ,…………7分
设 ,则 ,……………8分
在 时 , 递减,所以 , 最大值为1.……………10分
(3)因为 , ,则 .
①当 时,因为 ,
所以 在 上单调递减.所以 .
试卷第5页,共5页
学科网(北京)股份有限公司所以 在 上无零点.……………………………………………………………12分
②当 时,因为 单调递增,且 , ,
所以存在 ,使 .
当 时, ;当 时, .
所以 在 上单调递减,在 上单调递增,且 .
所以 .设 , ,
, ,……………………………………………14分
所以φ(x)在 上单调递减,在 上单调递增.
所以 .
所以 ,所以 .
所以 在 上存在一个零点.
所以 在 有2个零点.……………………………………………………………16分
综上所述, 在 上的零点个数为2…………………………………………17分
试卷第6页,共5页