理数_2024年4月_01按日期_16号_2024届四川绵阳南山中学高三4月绵阳三诊热身考试_四川省绵阳南山中学2024届高三下学期4月绵阳三诊热身考试数学（理）

2024年4月 绵阳南山中学高 2021 级高三下期绵阳三诊热身考试试题 理科数学 命题：汪琨 审题：黄磊 一、选择题：（本题共12小题，每小题5分，共60分。） 1．已知集合M   x∣x23x40  ,N {x∣yln(x1)}，则M N （ ） A．(1,4) B．[1,4) C．(1,4) D．[1,4)   2．若复数z满足z 3i 2，则 z （ ） A．1 B． 2 C． 3 D．2 x2 y2 3．已知双曲线  1的渐近线方程为y 3x，则a（ ）． a2 3 A．1 B．1 C．3 D．3       1        4．已知向量a,b 满足 a 2,b 5，且a与b 夹角的余弦值为 ，则 a2b  2ab （ ） 5 A．36 B．36 C．32 D．32 5．已知数列a 是首项为1的等比数列，S 是数列a 的前n项和，且9S S ，则数列 n n n 3 6 a 的前5项和为（ ） n A．30或40 B．31或40 C．31 D．30 6．点P在圆C：x42y42 9上，A3,0，B0,1，则PBA最小时，PB （ ） A．8 B．6 C．4 D．2 7．某几何体的三视图如图所示（单位：cm），则该几何体的表面积 （单位：cm2）是（ ） A．24 B．28 C．32 D．36 8．若ABC的内角A，B，C的对边分别为a，b，c，ABC的面积 S a2sinC，c6，角C平分线CM交边AB于点M，则AM的长为（ ） 第1页，共4页 {#{QQABCQiAggiAAIIAARgCUQXyCkAQkBACAIoOQAAEoAAByAFABAA=}#}A．2 B．4 C．2 2 D．2 3 π π π 9 ． 设 函 数 f(x)2sin(x ),(0), 若 存 在 x,x [ , ], 且 x  x ， 使 得 6 1 2 3 3 1 2 f x  f x 1，则的取值范围是（ ） 1 2 A． 4, B．4,6  C． 6, D．6,10  10．将甲、乙、丙、丁4名医生随机派往①，②，③三个村庄进行义诊活动，每个村庄至 少派1名医生，A表示事件“医生甲派往①村庄”； B表示事件“医生乙派往①村庄”； C 表示事件“医生乙派往②村庄”，则（ ） A．事件A与B相互独立 B．事件A与C相互独立 5 5 C． PB|A D． PC|A 12 12 11．若实数x，y满足4lnx2ln yx24y4 ，则（ ） 2 A．xy B．xy 2 C．x y1 2 D．x3y1 2 x2 y2 12．已知椭圆C：  1ab0的左、右焦点分别为F、F ，以F 为圆心的圆与x a2 b2 1 2 2 轴交于F，B两点，与y轴正半轴交于点A，线段AF 与C交于点M .若 BM 与C的焦距 1 1 31 的比值为 ，则C的离心率为（ ） 3 31 1 31 71 A． B． C． D． 2 2 4 2 二、填空题:（本题共4小题，每小题5分，共20分。） 13．x yx2y5的展开式中x4y2的系数为 ．（用数字作答）  π 3 5  3π 14．已知x  0,  ,sinxcosx ，则tanx  ．  4 5  4  1 x 15．若x,x 是函数 f x ax2ex1aR 的两个极值点，且 2 2，则实数a的取值 1 2 2 x 1 范围为 ． 第2页，共4页 {#{QQABCQiAggiAAIIAARgCUQXyCkAQkBACAIoOQAAEoAAByAFABAA=}#}4 3 16．将正方形ABCD沿对角线BD折起，当AC 2 3时，三棱锥ABCD的体积为 ， 3 则该三棱锥外接球的体积为 ． 三、解答题:（共70分） 17．一个盒子中装有大量形状大小一样但重量不尽相同的小球，从中随机抽取50个作为 样本，称出它们的重量(单位：克)，重量分组区间为5,15 , 15,25  , 25,35  , 35,45 ，由 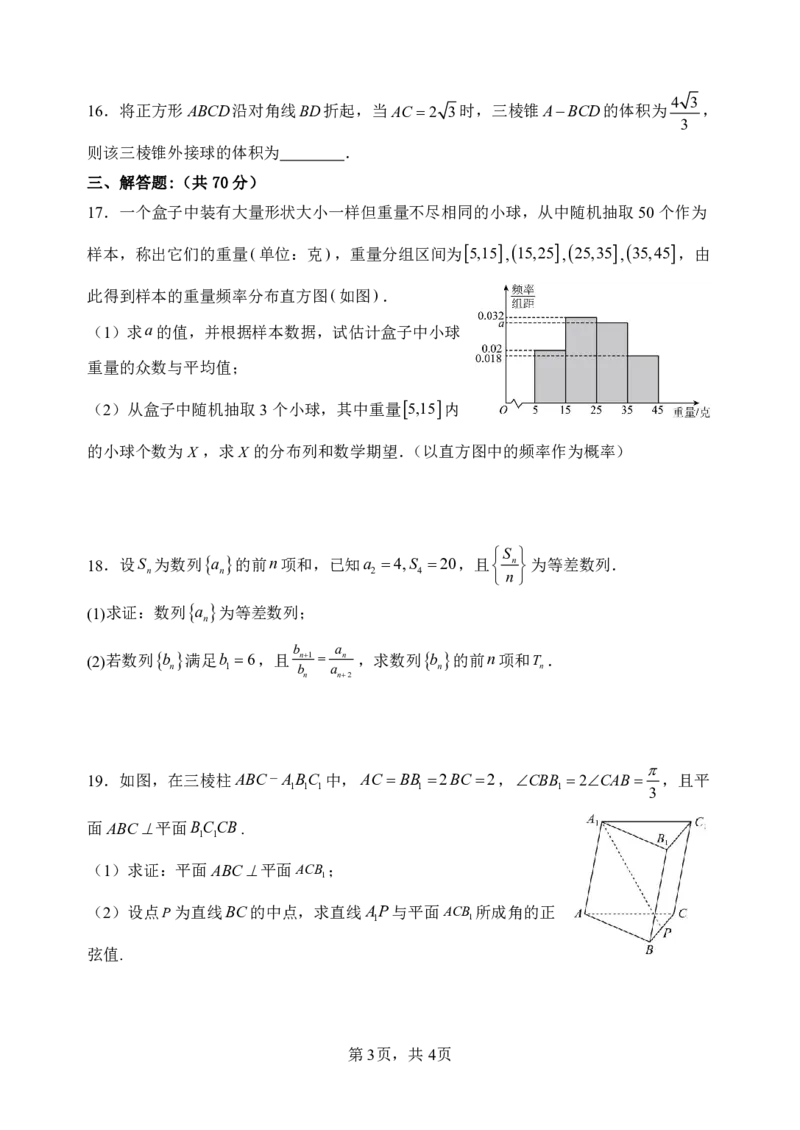此得到样本的重量频率分布直方图(如图)． （1）求a的值，并根据样本数据，试估计盒子中小球 重量的众数与平均值； （2）从盒子中随机抽取3个小球，其中重量5,15内 的小球个数为X ，求X 的分布列和数学期望．（以直方图中的频率作为概率） S  18．设S 为数列a 的前n项和，已知a 4,S 20，且 n为等差数列． n n 2 4  n  (1)求证：数列a 为等差数列； n b a (2)若数列b 满足b 6，且 n1  n ，求数列b 的前n项和T ． n 1 b a n n n n2  19．如图，在三棱柱ABC-ABC 中，AC BB 2BC2，CBB 2CAB ，且平 1 1 1 1 1 3 面ABC平面BCCB. 1 1 （1）求证：平面ABC平面ACB ； 1 （2）设点P为直线BC的中点，求直线AP与平面ACB 所成角的正 1 1 弦值. 第3页，共4页 {#{QQABCQiAggiAAIIAARgCUQXyCkAQkBACAIoOQAAEoAAByAFABAA=}#}20．已知函数 f xae2xa2exx （1）讨论 f x的单调性； （2）若 f x有两个零点，求a的取值范围. 21．已知点E  1,2 2  在抛物线C:y2 2pxp 0上，A,B为抛物线C上两个动点，AB 不垂直x轴，F 为焦点，且满足 AF  BF 8． (1)求p的值，并证明：线段AB的垂直平分线过定点； (2)设（1）中定点为M ，当ABM 的面积最大时，求直线AB的方程．  π 1 22．在极坐标系中，曲线C 的极坐标方程为ρsinθ  0，以极点为坐标原点，极 1  3 2 x2cos 轴为x轴正半轴，建立直角坐标系，曲线C 的参数方程为 （为参数）. 2 y2sin (1)写出C 的直角坐标方程和C 的普通方程； 1 2 1 1 (2)已知点P0,1，C 与C 相交于A，B两点，求  的值. 1 2 PA PB 23．已知x、y、z均为正实数，且4x2y2z2 3． (1)求2x yz的最大值； 1 1 (2)若y2x，证明：  3． x z 第4页，共4页 {#{QQABCQiAggiAAIIAARgCUQXyCkAQkBACAIoOQAAEoAAByAFABAA=}#}