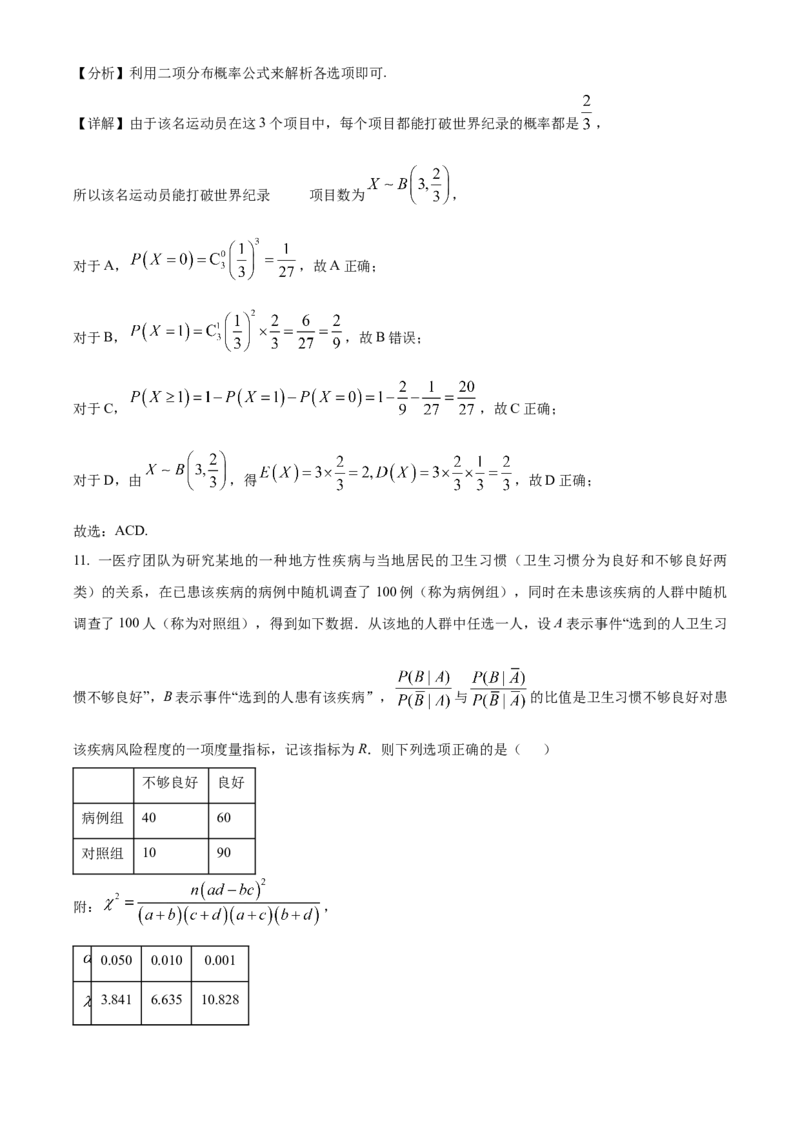文档内容
2024-2025 学年下学期高二年级
数学 学科阶段验收考试试卷
考试时间:90分钟 满分:120分
命题人:杨志勇 付盼盼 审题人:杨志勇 付盼盼
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一个选项是符合题目要求的.
1. 已知数列 的通项公式为 ,则146是该数列的( )
A. 第10项 B. 第11项 C. 第12项 D. 第13项
【答案】C
【解析】
【分析】根据给定的通项公式,列式求出 值即可.
【详解】依题意, ,而 ,解得 ,
所以146是该数列的第12项.
故选:C
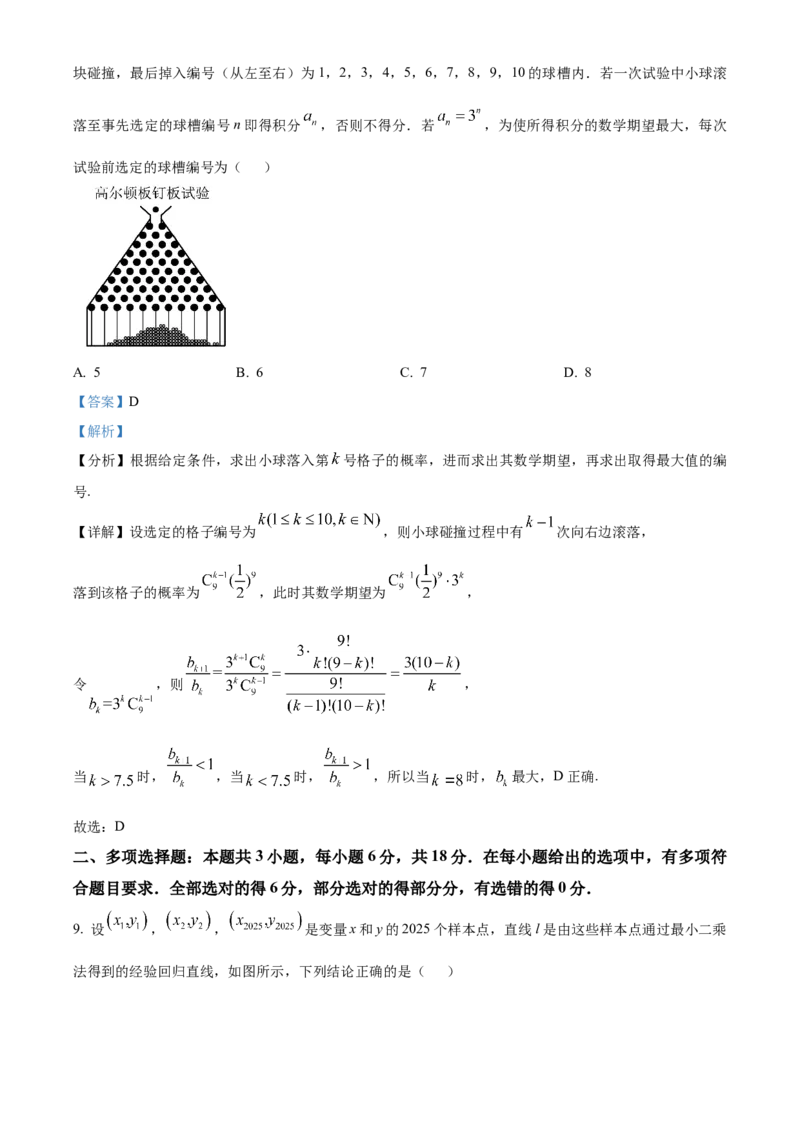
2. 对变量x,y由观测数据 得散点图1;对变量u,v由观测数据 得散点图
2. 表示变量x,y之间的线性相关系数, 表示变量u,v之间的线性相关系数,则下列说法正确的是(
)
A. 变量x与y呈现正相关,且 B. 变量x与y呈现负相关,且
C. 变量u与v呈现正相关,且 D. 变量u与v呈现负相关,且
【答案】A【解析】
【分析】利用散点图,结合相关系数的知识可得答案.
【详解】观察散点图,得变量x与y呈现正相关,变量u与v呈现负相关,BC错误;
图1中各点比图2中各点更加集中,相关性更好,因此 ,A正确,D错误.
故选:A
3. 若随机变量 服从两点分布, ,则 为( )
A. 0.3 B. 0.35 C. 0.6 D. 0.65
【答案】B
【解析】
【分析】根据题意,得到 ,结合 ,列出方程,
求得 ,进而求得 的值,即可求解.
【详解】由随机变量 服从两点分布,则 ,
因为 ,可得 ,解得 ,
.
所以
故选:B.
4. 已知随机变量 ,且 ,则 ( )
A. 0.2 B. 0.3 C. 0.7 D. 0.8
【答案】B
【解析】
【分析】根据给定条件,利用正态分布的对称性求出概率.
【详解】随机变量 ,且 ,
则 .
故选:B
5. 已知盒子中有6个大小相同的球,分别标有数字1,2,3,4,5,6,从中不放回地随机取两球,每次取一球,记第一次取出的球的数字是 ,第二次取出的球的数字是 .若事件 “ 为偶数”,事件
“ , 中有偶数”,则 ( )
A. B. C. D.
【答案】C
【解析】
【分析】先根据题意求出 ,然后利用条件概率公式求解即可.
【详解】由题意得 ,
所以 .
故选:C
6. 数学老师从6道题中随机抽3道让同学检测,规定至少要解答正确2道题才能及格.某同学只能正确求
解其中的4道题,则该同学能及格的概率为( )
A. B. C. D.
【答案】A
【解析】
【分析】利用超几何分布的概率公式计算即可.
【详解】由题意知抽取3道题该同学不及格的情况只有:只对一道题一种情况,
则只答对一道题的概率为 ,所以该同学及格的概率为 .
故选:A
7. 云计算是信息技术发展的集中体现,近年来,我国云计算市场规模持续增长. 已知某科技公司2018年至
2022年云计算市场规模数据,且市场规模 与年份代码 的关系可以用模型 (其中 为自然对数的底数)拟合,设 ,得到数据统计表如下:
年份 2018年 2019年 2020年 2021年 2022年
年份代码 1 2 3 4 5
2 2.4 3 3.6 4
由上表可得经验回归方程 ,则2026年该科技公司云计算市场规模 的估计值为( )
(参考公式: )
A. B. C. D.
【答案】C
【解析】
【分析】根据 可得线性回归方程,再由回归方程求出2026年z的预测值,代入 即可得
解.
【详解】因为
所以
即经验回归方程
当 时,
所以
即2026年该科技公司云计算市场规模y的估计值为 .
故选:C.
8. 高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型.在一块木板上钉着若干排相互平行
但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃.每次试验时,让
一个小球从高尔顿板上方的通道口落下,小球在下落过程中与层层小木块碰撞,且等可能向左或向右滚下,
最后掉入高尔顿板下方的某一球槽内,在如图所示的小木块中,上面10层为高尔顿板,最下面为球槽.小
球从通道口落下,第一次与第2层中间的小木块碰撞,以 的概率向左或向右滚下,依次经过9次与小木块碰撞,最后掉入编号(从左至右)为1,2,3,4,5,6,7,8,9,10的球槽内.若一次试验中小球滚
落至事先选定的球槽编号n即得积分 ,否则不得分.若 ,为使所得积分的数学期望最大,每次
试验前选定的球槽编号为( )
A. 5 B. 6 C. 7 D. 8
【答案】D
【解析】
【分析】根据给定条件,求出小球落入第 号格子的概率,进而求出其数学期望,再求出取得最大值的编
号.
【详解】设选定的格子编号为 ,则小球碰撞过程中有 次向右边滚落,
落到该格子的概率为 ,此时其数学期望为 ,
令 ,则 ,
当 时, ,当 时, ,所以当 时, 最大,D正确.
故选:D
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符
合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 设 , , 是变量x和y的2025个样本点,直线l是由这些样本点通过最小二乘
法得到的经验回归直线,如图所示,下列结论正确的是( )A. 直线l一定过点
B. 直线l一定过点
C. x和y的样本相关系数在区间 上
D. 因为2025是奇数,所以分布在直线l两侧的样本点的个数一定不相同
【答案】AC
【解析】
【分析】经验回归方程一定过样本中心点,但不一定过某个样本点,可判断A B,根据图象特点可判断
CD.
【详解】对于A、B,经验回归方程一定过样本中心点,但不一定过某个样本点,故A正确,B错误;
对于C,由题图可知x和y是负相关,则样本相关系数在区间 上,故C正确;
对于D,不能因为2025是奇数就断定分布在直线l两侧的样本点的个数不相同,故D错误.
故选:AC
10. 在一次国际大型体育运动会上,某运动员报名参加了其中3个项目的比赛.已知该运动员在这3个项目
中,每个项目能打破世界纪录的概率都是 ,设该运动员能打破世界纪录的项目数为X,那么在本次运动
会上( )
A. B.
C. D. ,
【答案】ACD
【解析】【分析】利用二项分布概率公式来解析各选项即可.
【详解】由于该名运动员在这3个项目中,每个项目都能打破世界纪录的概率都是 ,
所以该名运动员能打破世界纪录 的项目数为 ,
对于A, ,故A正确;
对于B, ,故B错误;
对于C, ,故C正确;
对于D,由 ,得 ,故D正确;
故选:ACD.
11. 一医疗团队为研究某地的一种地方性疾病与当地居民的卫生习惯(卫生习惯分为良好和不够良好两
类)的关系,在已患该疾病的病例中随机调查了100例(称为病例组),同时在未患该疾病的人群中随机
调查了100人(称为对照组),得到如下数据.从该地的人群中任选一人,设A表示事件“选到的人卫生习
惯不够良好”,B表示事件“选到的人患有该疾病”, 与 的比值是卫生习惯不够良好对患
该疾病风险程度的一项度量指标,记该指标为R.则下列选项正确的是( )
不够良好 良好
病例组 40 60
对照组 10 90
附: ,
0.050 0.010 0.001
3.841 6.635 10.828A. 依据 的独立性检验,可推断患该疾病群体与未患该疾病群体的卫生习惯有差异
B. 利用该调查数据,可得到 的估计值为0.4, 的估计值为0.1
C. .
D. 利用该调查数据,可得到R的估计值为5
【答案】ABC
【解析】
【分析】对于选项A,可由列联表,结合所给公式,求出 的值,根据小概率值的独立性检验,即可判
断;对于选项B,由已知条件,可直接求得 的值,即可判断;对于选项C,可利用公式
证 明 ; 对 于 选 项 D , 由 已 知 条 件 , 分 别 求 出
的值,即可求出R的值,即可判断.
【详解】对于选项A,由列联表得
所以根据小概率值 的独立性检验,认为患该疾病群体与未患该疾病群体的卫生习惯有差异,故选
项A正确;
对于选项B,由已知得 故选项B正确;
对于选项C,由题意得 ,
又所以 ,故选项C正确;
对于选项D,由已知得 ,
所以 ,故选项D错误.
故答案选:ABC.
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知数列 的前n项和 ,则通项 ______.
【答案】
【解析】
【分析】根据给定条件,利用前n项与第 项的关系求出通项公式.
【详解】数列 的前n项和 ,
当 时, ,而 ,满足上式,
所以 .
故答案为:
13. 设某批产品中,甲、乙、丙三厂生产的产品分别占55%,25%,20%,各厂的产品的次品率分别为
2%,4%,5%.现从中任取一件,则取到的是次品的概率是______.
【答案】
【解析】
【分析】根据题意,结合全概率公式 ,代入计
算,即可求解.
【详解】设 表示“取到一件次品”, 表示“取到的产品由甲乙丙三厂生产的,其中 ”,
则 ,且 ,
由全概率公式,可得
,
即取到的是次品的概率是 .
故答案为: .
14. 对一个物理量做n次测量,并以测量结果的平均值作为该物理值的最后结果.已知最后结果的误差
,为使误差 在 的概率不小于 0.9973、至少要测量______次.(若
,则 )
【答案】48
【解析】
【分析】利用正态分布的三段区间概率公式及性质计算即可.
【详解】由误差 ,得 ,
由误差 在 的概率不小于0.9973,得 ,
因此 ,解得 ,于是 ,解得 ,
所以至少要测量48次.
故答案为:48
四、解答题:本题共4小题,共47分.解答应写出文字说明、证明过程或演算步骤.
15. 袋中装有5个乒乓球,其中2个旧球,现在无放回地每次取一球检验.
(1)若直到取到新球为止,求抽取次数X的概率分布及其均值;
(2)若将题设中的“无放回”改为“有放回”,求检验5次取到新球个数X的均值.
【答案】(1)概率分布见解析,(2)3
【解析】
【分析】(1)由分布列及均值定义计算即可得;
(2)由二项分布均值公式计算即可得.
【小问1详解】
X的可能取值为1,2,3, ,
故抽取次数X的概率分布为:
X 1 2 3
P
;
【
小问2详解】
每次检验取到新球的概率均为 ,故 ,所以 .
16. 近几年我国新能源汽车产业快速发展,据行业数据显示,新能源汽车的数量在不断增加.下表为某城市
统计的近5年新能源汽车的新增数量,其中 为年份代号, (单位:万辆)代表新增新能源汽车的数量.
年份 2020 2021 2022 2023 2024
年份代号 1 2 3 4 5
新增新能源汽车 万
1.2 1.8 2.5 3.2 3.8
辆
(1)计算样本相关系数 ,判断是否可以用线性回归模型拟合 与 的关系,当 时,可以认
为两个变量有很强的线性相关性;否则,没有很强的线性相关性.
(2)求 关于 的经验回归方程,并据此估计该城市2026年的新增新能源汽车的数量;
参考数据: .参考公式:.
【答案】(1)可以用线性回归模型拟合 与 的关系.
(2) ,估计该市2026年新增燃油车5.14万辆.
【解析】
的
【分析】(1)根据题意求相关系数r,结合相关系数 性质分析理解;
(2)根据题意求得回归方程为 ,令 ,代入运算即可得结果.
【小问1详解】
由题意可得: ,
则
,
因为 ,故可以用线性回归模型拟合 与 的关系.
【小问2详解】
由题意可得: , ,
则 ,当 时, ,
所以估计该市2026年新增燃油车5.14万辆.
17. 椭圆 的左、右焦点分别是 、 ,离心率为 ,过 且垂直于x轴的直线被椭圆C截得的线段长为3.
(1)求椭圆C的方程;
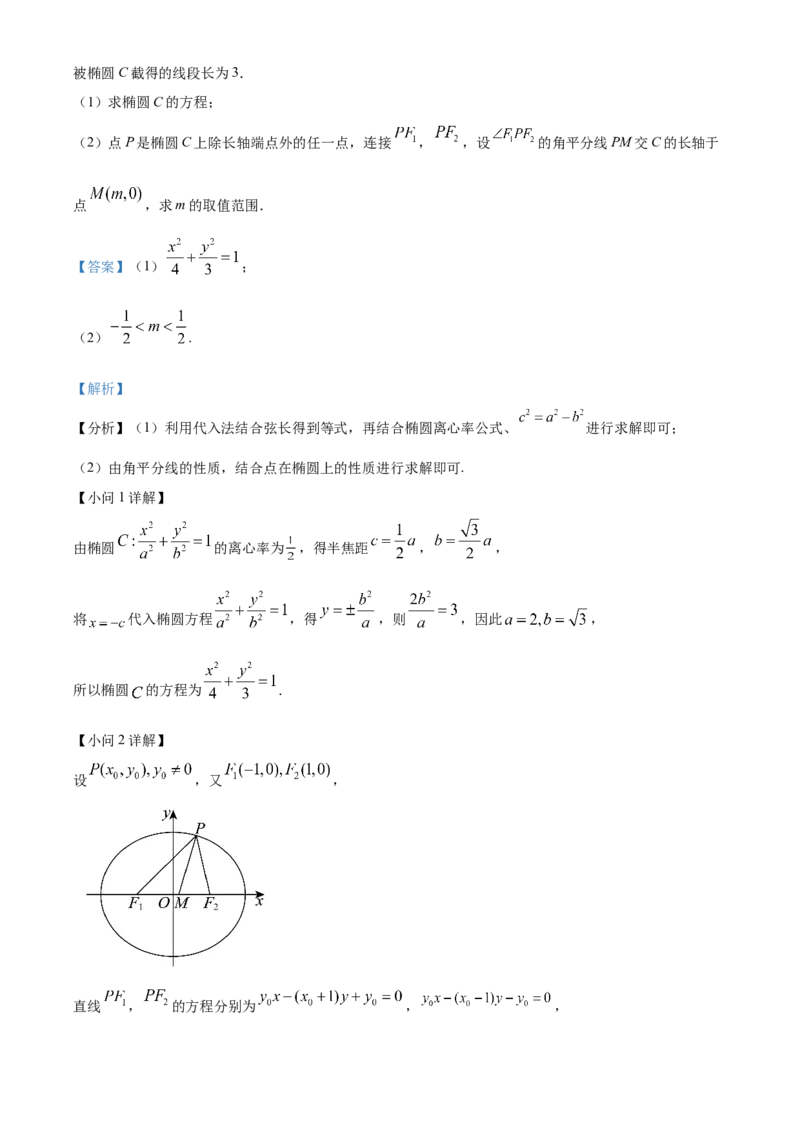
(2)点P是椭圆C上除长轴端点外的任一点,连接 , ,设 的角平分线PM交C的长轴于
点 ,求m的取值范围.
【答案】(1) ;
(2) .
【解析】
【分析】(1)利用代入法结合弦长得到等式,再结合椭圆离心率公式、 进行求解即可;
(2)由角平分线的性质,结合点在椭圆上的性质进行求解即可.
【小问1详解】
由椭圆 的离心率为 ,得半焦距 , ,
将 代入椭圆方程 ,得 ,则 ,因此 ,
所以椭圆 的方程为 .
【小问2详解】
设 ,又 ,
直线 , 的方程分别为 , ,由 的角平分线PM交C的长轴于点 ,得 ,
由点 在椭圆上,得 ,即 ,则 ,
又 , ,于是 , ,
所以m的取值范围是 .
18. 甲参加某多轮趣味游戏,在A,B两个不透明的盒内摸球,规定在一轮游戏中甲先在A盒内随机取出1
个小球放入B盒,再在B盒内随机取出2个小球.若每轮游戏的结果相互独立,且每轮游戏开始前,两盒
内小球的数量始终如下表(小球除颜色外大小质地完全相同):
红球 蓝球 白球
A
2 2 1
盒
B
2 2 1
盒
(1)求在一轮游戏中甲从A,B两盒内取出的小球均为白球的概率:
(2)已知每轮游戏的得分规则为:若从B盒内取出的小球均为红球,则甲获得5分;若从B盒内取出的
小球中只有1个红球,则甲获得3分;若从B盒内取出的小球没有红球,则甲获得1分.
(i)记甲在一轮游戏中的得分为X,求X的分布列:
(ii)在 的条件下,从A盒取出放入B盒的球最有可能是什么颜色?
【答案】(1) ;
(2)(i)分布列见解析;(ii)红球
【解析】
【分析】(1)记“在一轮游戏中甲从 两盒内取出的小球均为白球”为事件 ,利用概率的乘法公式求得 ,即可求解;
(2)(i)由题意得到随机变量 可以取 ,利用全概率的概率公式求得相应的概率,列出分布列;
(ii)利用全概率公式计算即可.
【小问1详解】
记“在一轮游戏中甲从 两盒内取出的小球均为白球”为事件 ,
所以由条件概率可知 ,
所以在一轮游戏中甲从 两盒内取出的小球均为白球的概率为 .
【小问2详解】
(i)由题意,可知随机变量 可以取 ,
可得 ,
,
,
所以随机变量 的分布列为
(ii)在 的条件下,从A盒取出红球的概率为 ,在 的条件下,从A盒取出蓝球的概率为 ,
在 的条件下,从A盒取出白球的概率为 ,
因 ,故在 的条件下,从A盒取出放入B盒的球最有可能是红球.