2025年新高考地区数学名校地市选填压轴题好题汇编（六）（学生版）_2024-2025高三（6-6月题库）_2024年11月试卷_11272025年新高考地区数学名校地市选填压轴题好题汇编（六）

年新高考地区数学名校地市选填压轴题好题汇编（六） 2025 lnx,x0  1．（广东省五校2023-2024学年高三10月联考（二）数学试题）设函数 f x 1 ，若方程 f xxb x ,x0  x 有3个不同的实根，则b的取值范围为（ ） A．,1 B．1,0 C．0,1 D．1, π 2．（广东省七校2024届高三第二次联考数学试卷）在直四棱柱ABCD ABCD 中，BAD ， 1 1 1 1 3 ABADAA 2，点Q在侧面DCCD 内，且AQ 7，则点Q轨迹的长度为（ ） 1 1 1 1 π π 2π 4π A． B． C． D． 6 3 3 3  1 3．（广东省七校2024届高三第二次联考数学试卷）已知a0，f xaex lnxb，当x0时，f x0，  x 则a1b3的最大值为（ ） 1 2 A． B． e2 e2 3 4 C． D． e2 e2 x2 4．（广东省（上进联考）2024届高三10月阶段检测考数学试题）已知D为双曲线C:  y2 1右支上一点， 4 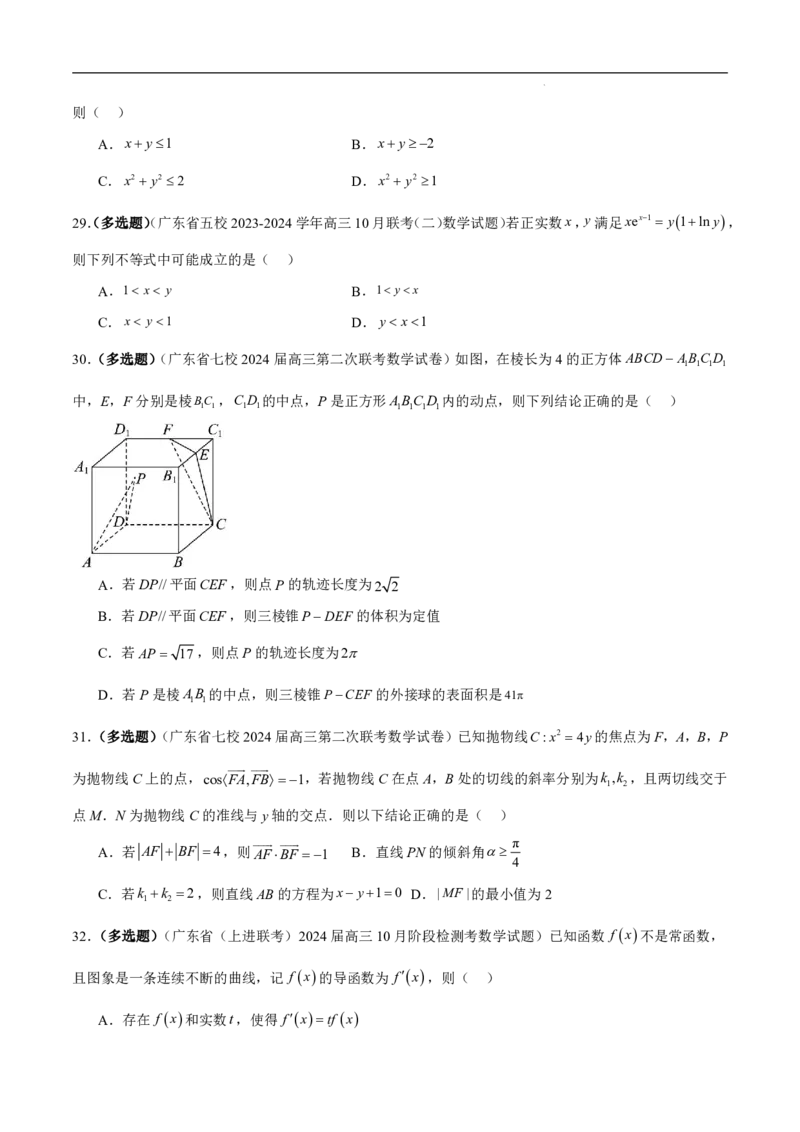过点D分别作C的两条渐近线的平行线，与另外一条渐近线分别交于点A,B，则 DA DB （ ） 5 5 A．2 B． 5 C． D． 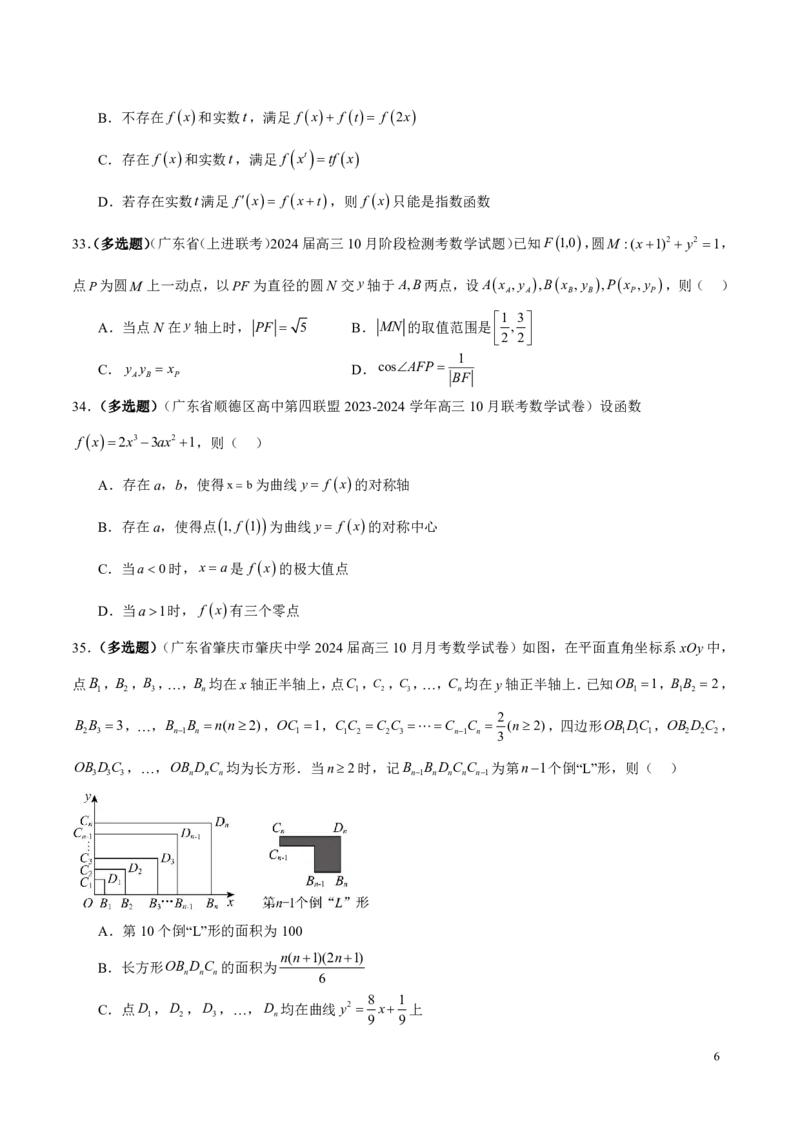4 2  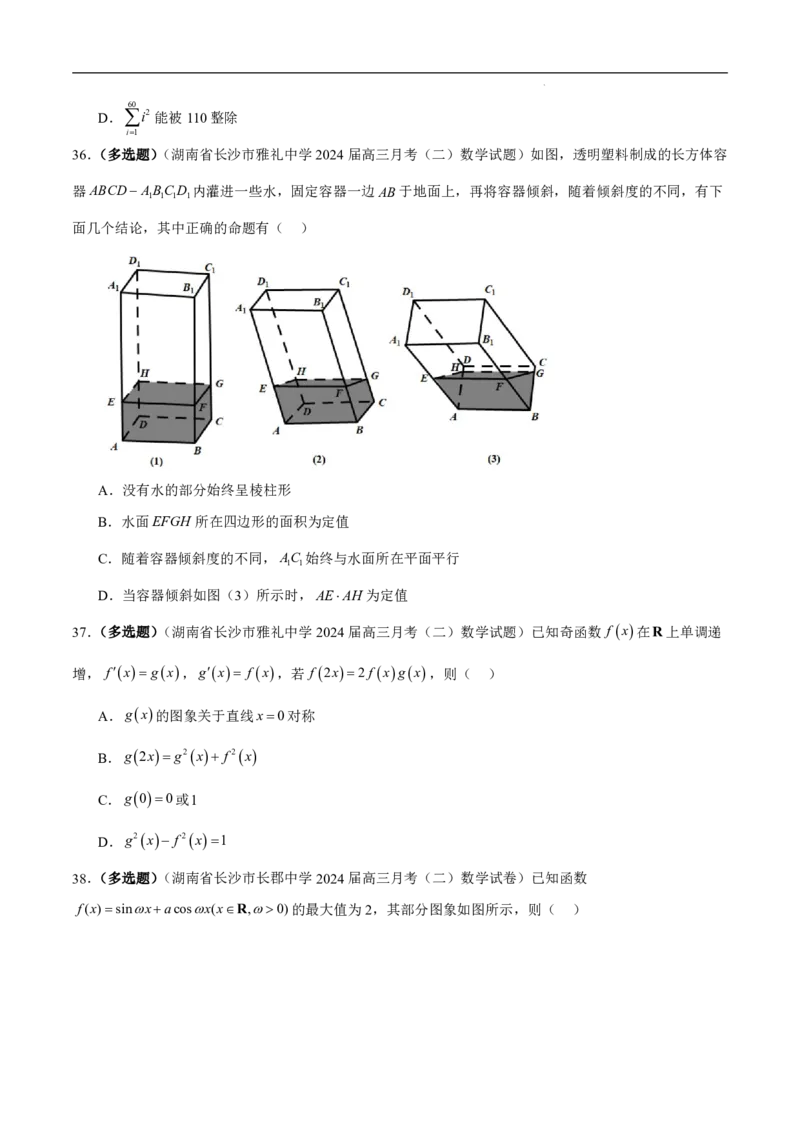lnx ,x0 5．（广东省顺德区高中第四联盟2023-2024学年高三10月联考数学试卷）设函数 f(x) ，若 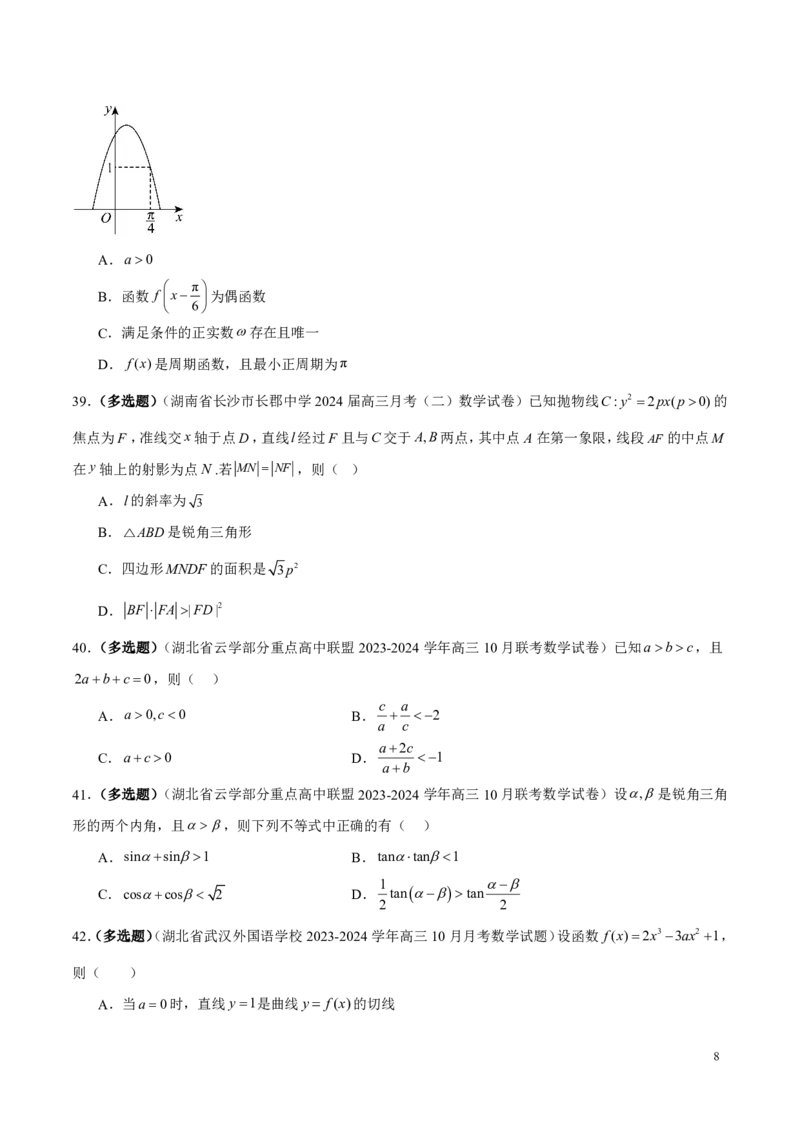ex(x1),x0 1 方程[f(x)]2af(x) 0有六个不等的实数根，则实数a可取的值可能是（ ） 16 2 2 2 A． B． 或1 C．1 D． 或2 3 3 3 x2 y2 6．（广东省顺德区高中第四联盟2023-2024学年高三10月联考数学试卷）已知椭圆E：  1的左右 16 4 2  3 1 顶点分别为A，A ，圆O 的方程为x12y   ，动点P在曲线E上运动，动点Q在圆O 上运动， 1 2 1   1  2  4 若△AA P的面积为4 3，记 PQ 的最大值和最小值分别为m和n，则mn的值为（ ） 1 2 A． 7 B．2 7 C．3 7 D．4 7 学科网（北京）股份有限公司7．（广东省肇庆市肇庆中学2024届高三10月月考数学试卷）已知函数 f xasin2xcos2x0图 π a  象的对称轴方程为xkπ ，kZ．则 f  π（ ） 4 4  2 2 A． B． C． 2 D． 2 2 2 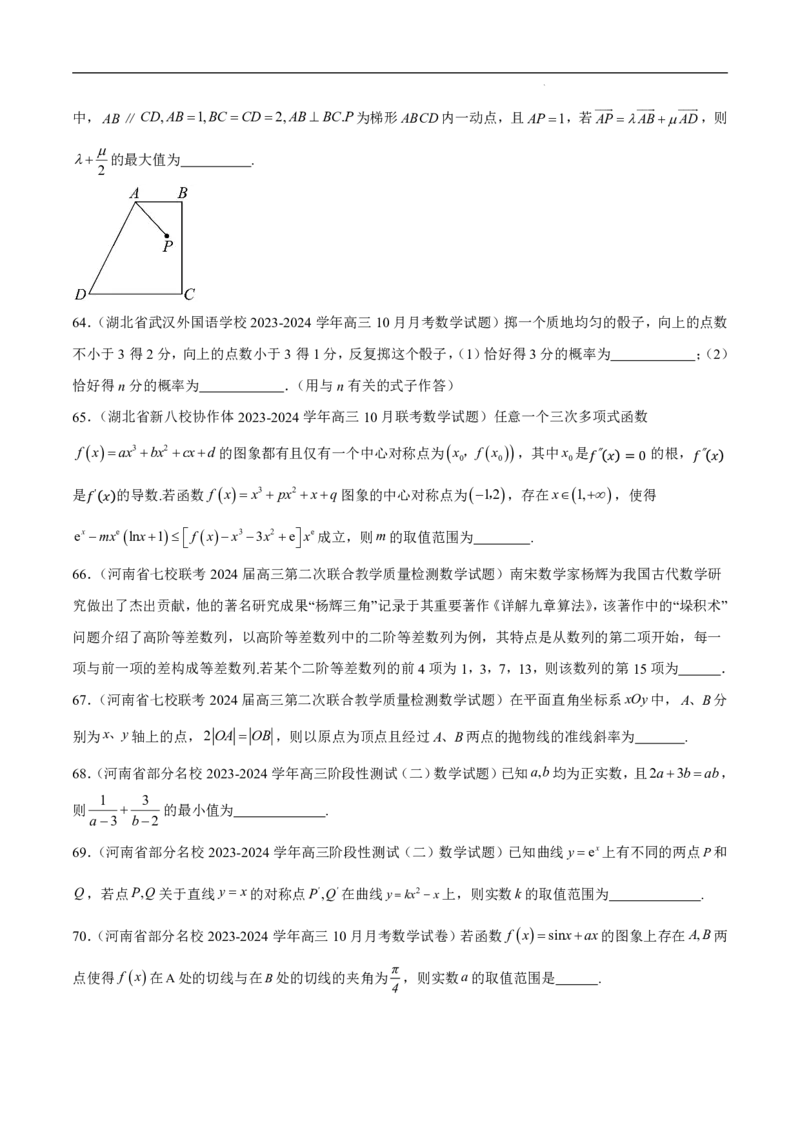8．（湖南省长沙市雅礼中学2024届高三月考（二）数学试题）若x，y0，x y1，则 3x y的取值 范围为（ ） A．  1, 3  B．1,2 C．  3,2  D．   1 , 3   2  9．（湖南省长沙市雅礼中学2024届高三月考（二）数学试题）已知抛物线C：x2 4y的焦点为F ，过点F 1 的直线与C相交于M ，N 两点，则2 MF  NF 的最小值为（ ） 2 9 7 A． B．4 C． D．3 2 2 10．（湖南省长沙市雅礼中学2024届高三月考（二）数学试题）从重量分别为1，2，3，4，…，10克的砝 码（每种砝码各2个）中选出若干个，使其总重量恰为9克的方法总数为m，下列各式的展开式中x9的系 数为m的选项是（ ） A．1x 1x2 1x3   1x10 B．1x12x13x  110x C．1x2 1x22 1x32 1x42   1x102 D．1x2 1xx22 1xx2x32   1xx2x102 11．（湖南省长沙市长郡中学2024届高三月考（二）数学试卷）在平面直角坐标系xOy中，已知直线 1 l:ykx 与圆C:x2 y2 1交于A,B两点，则VAOB的面积的最大值为（ ） 2 1 3 3 A．1 B． C． D． 2 2 4 12．（湖南省长沙市长郡中学2024届高三月考（二）数学试卷）设函数 f x  x2axb  lnx，若 f x0， 则a的最小值为（ ） A．2 B．1 C．2 D．1 13．（湖北省云学部分重点高中联盟2023-2024学年高三10月联考数学试卷）在平面直角坐标系中，双曲线 x2 y2 C:  1  a0,b0 的左､右焦点分别为F,F ,A为双曲线右支上一点，连接AF 交y轴于点B，若 a2 b2 1 2 1 2AB  AF ，且AF  AF ，则双曲线的离心率为（ ） 2 1 2 A． 1 2 B． 2 2 C． 5 D． 6 14．（湖北省云学部分重点高中联盟2023-2024学年高三10月联考数学试卷）已知函数 f xcosxax在  π 区间 0, 单调递增，则实数a的取值范围是（ ）    6  1  3 1   3  A．,  B．  ,  C．  , D． ,   2  2  2   2   1 15．（湖北省云学部分重点高中联盟2023-2024学年高三10月联考数学试卷）已知函数 f xlnxax   x 有两个极值点x ,x ，则 f x x 的取值范围是（ ） 1 2 1 2  3  3   3  3  A．0,ln2  B．ln2 , C．0,2ln2  D．ln2 ,  4  2   2  4  16．（湖北省武汉外国语学校2023-2024学年高三10月月考数学试题）已知aR，设函数 x22ax2a, x1, f(x) 若关于x的不等式 f(x)0在R上恒成立，则a的取值范围为 xalnx, x1, A．0,1 B． 0,2  C．  0,e  D．1,e 17．（湖北省武汉外国语学校2023-2024学年高三10月月考数学试题）已知函数 f x f x,xR， f 5.51，函数gxx1 f x，若gx1为偶函数，则g0.5的值为（ ） A．3 B．2.5 C．2 D．1.5 18．（湖北省新八校协作体2023-2024学年高三10月联考数学试题）已知函数 f x的定义域为R， y f x2ex是偶函数，y f x4ex是奇函数，则 f x的最小值为（ ） A．e B．2 2 C．2 3 D．2e lnx  ,x0 19．（湖北省新八校协作体2023-2024学年高三10月联考数学试题）已知函数 f x   x ，若函数  ex  ,x0  x xk gx f x 恰有2个零点，则实数k的取值范围是（ ） x A．1,e B．，1 e， C．[1,1) D．，11， 学科网（北京）股份有限公司22．（河南省七校联考2024届高三第二次联合教学质量检测数学试题）如图所示，直线ykxm与曲线 相切于  x, f x  ,  x , f x  两点，其中x x ．若当x0,x 时，fxk，则函数 f xkx在 = 1 1 2 2 1 2 1 上的极大值点个数为（ ） 0,+ ∞ A．0 B．1 C．2 D．3  π 23．（河南省部分名校2023-2024学年高三阶段性测试（二）数学试题）将函数 f(x)cosx (06)  6 π 的图象向右平移 个单位长度得到函数g(x)的图象，若g(x)是奇函数，则 f(x)在区间(0,π)内的极值点个 6 数为（ ） A．1 B．2 C．3 D．4 24．（河南省部分名校2023-2024学年高三阶段性测试（二）数学试题）已知函数 f x的定义域为R, f x1 为奇函数， f x2为偶函数，则 f 1 f 2L f 16（ ） A．0 B．16 C．22 D．32 25．（河南省部分名校2023-2024学年高三10月月考数学试卷）已知函数 f x及其导函数 的定义域均 ' 20 为 ，若 f x f x2x, f x的图象关于直线x1对称，且 f 20，则 f(20)f(i)（ ） i1 A．10 B．20 C．10 D．20 26．（河南省部分名校2024届高三月考（一）数学试题）VABC与△ABD都是边长为2的正三角形，沿公 共边AB折叠成三棱锥且CD长为 3 ，若点A，B，C，D在同一球O的球面上，则球O的表面积为（ ） 13 208π 112π 52 A． π B． C． D． π 9 9 3 9 27．（河南省部分名校2024届高三月考（一）数学试题）已知函数 f x及其导函数 fx在定义域均为R且 Fxex2f x2是偶函数，其函数图象为不间断曲线且x2 fx f x  0，则不等式 xf lnxe3f 3的解集为（ ） A．  0,e3 B．  1,e3 C．  e,e3 D．  e3,  28．（多选题）（广东省五校2023-2024学年高三10月联考（二）数学试题）若x，y满足x2  y2 xy1， 4则（ ） A．xy1 B．xy2 C．x2 y2 2 D．x2 y2 1 29．（多选题）（广东省五校2023-2024学年高三10月联考（二）数学试题）若正实数x，y满足xex1  y1lny， 则下列不等式中可能成立的是（ ） A．1 x y B．1 yx C．x y 1 D．y x1 30．（多选题）（广东省七校2024届高三第二次联考数学试卷）如图，在棱长为4的正方体ABCD ABCD 1 1 1 1 中，E，F分别是棱BC ，C D 的中点，P是正方形ABCD 内的动点，则下列结论正确的是（ ） 1 1 1 1 1 1 1 1 A．若DP//平面CEF，则点P的轨迹长度为2 2 B．若DP//平面CEF，则三棱锥PDEF的体积为定值 C．若AP 17，则点P的轨迹长度为2 D．若P是棱AB 的中点，则三棱锥PCEF 的外接球的表面积是 1 1 31．（多选题）（广东省七校2024届高三第二次联考数学试卷）已知抛物线C:x2 4y的焦点为F，A，B，P   为抛物线C上的点，cosFA,FB1，若抛物线C在点A，B处的切线的斜率分别为k ,k ，且两切线交于 1 2 点M．N为抛物线C的准线与y轴的交点．则以下结论正确的是（ ）   π A．若 AF  BF 4，则 AFBF 1 B．直线PN的倾斜角 4 C．若k k 2，则直线AB的方程为xy10 D．|MF |的最小值为2 1 2 32．（多选题）（广东省（上进联考）2024届高三10月阶段检测考数学试题）已知函数 f x不是常函数， 且图象是一条连续不断的曲线，记 f x的导函数为 fx，则（ ） A．存在 f x和实数t，使得 fxtf x 学科网（北京）股份有限公司B．不存在 f x和实数t，满足 f x f t f 2x C．存在 f x和实数t，满足 f  xt tf x D．若存在实数t满足 fx f xt，则 f x只能是指数函数 33．（多选题）（广东省（上进联考）2024届高三10月阶段检测考数学试题）已知F1,0，圆M :(x1)2 y2 1， 点P为圆M 上一动点，以PF 为直径的圆N 交y轴于A,B两点，设Ax ,y ,Bx ,y ,Px ,y ，则（ ） A A B B P P 1 3 A．当点N 在y轴上时， PF  5 B． MN 的取值范围是  ,  2 2 1 C．y y  x D．cosAFP A B P BF 34．（多选题）（广东省顺德区高中第四联盟2023-2024学年高三10月联考数学试卷）设函数 f x2x33ax21，则（ ） A．存在a，b，使得xb为曲线y f x的对称轴 B．存在a，使得点  1, f 1 为曲线y f x的对称中心 C．当a0时，xa是 f x的极大值点 D．当a1时， f x有三个零点 35．（多选题）（广东省肇庆市肇庆中学2024届高三10月月考数学试卷）如图，在平面直角坐标系xOy中， 点B ，B ，B ，…，B 均在x轴正半轴上，点C ，C ，C ，…，C 均在y轴正半轴上．已知OB 1，BB 2， 1 2 3 n 1 2 3 n 1 1 2 2 B B 3，…，B B n(n2)，OC 1，CC C C C C  (n2)，四边形OBDC ，OB DC ， 2 3 n1 n 1 1 2 2 3 n1 n 3 1 1 1 2 2 2 OB DC ，…，OB DC 均为长方形．当n2时，记B B DC C 为第n1个倒“L”形，则（ ） 3 3 3 n n n n1 n n n n1 A．第10个倒“L”形的面积为100 n(n1)(2n1) B．长方形OB DC 的面积为 n n n 6 8 1 C．点D ，D ，D ，…，D 均在曲线y2  x 上 1 2 3 n 9 9 660 D．i2 能被110整除 i1 36．（多选题）（湖南省长沙市雅礼中学2024届高三月考（二）数学试题）如图，透明塑料制成的长方体容 器ABCD ABCD 内灌进一些水，固定容器一边AB于地面上，再将容器倾斜，随着倾斜度的不同，有下 1 1 1 1 面几个结论，其中正确的命题有（ ） A．没有水的部分始终呈棱柱形 B．水面EFGH 所在四边形的面积为定值 C．随着容器倾斜度的不同，AC 始终与水面所在平面平行 1 1 D．当容器倾斜如图（3）所示时，AEAH为定值 37．（多选题）（湖南省长沙市雅礼中学2024届高三月考（二）数学试题）已知奇函数 f x在R上单调递 增， fx gx，gx f x，若 f 2x2f xgx，则（ ） A．gx的图象关于直线x0对称 B．g2xg2x f2x C．g00或1 D．g2x f2x1 38．（多选题）（湖南省长沙市长郡中学2024届高三月考（二）数学试卷）已知函数 f(x)sinxacosx(xR,0)的最大值为2，其部分图象如图所示，则（ ） 学科网（北京）股份有限公司A．a0  π B．函数 f x 为偶函数  6 C．满足条件的正实数存在且唯一 D． f(x)是周期函数，且最小正周期为π 39．（多选题）（湖南省长沙市长郡中学2024届高三月考（二）数学试卷）已知抛物线C:y2 2px(p0)的 焦点为F ，准线交x轴于点D，直线l经过F 且与C交于A,B两点，其中点A在第一象限，线段AF的中点M 在y轴上的射影为点N .若 MN  NF ，则（ ） A．l的斜率为 3 B．△ABD是锐角三角形 C．四边形MNDF的面积是 3p2 D． BF  FA |FD|2 40．（多选题）（湖北省云学部分重点高中联盟2023-2024学年高三10月联考数学试卷）已知abc，且 2abc0，则（ ） c a A．a0,c0 B．  2 a c a2c C．ac0 D． 1 ab 41．（多选题）（湖北省云学部分重点高中联盟2023-2024学年高三10月联考数学试卷）设,是锐角三角 形的两个内角，且，则下列不等式中正确的有（ ） A．sinsin1 B．tantan1 1  C．coscos 2 D． tantan 2 2 42．（多选题）（湖北省武汉外国语学校2023-2024学年高三10月月考数学试题）设函数 f(x)2x33ax21， 则（ ） A．当a0时，直线y1是曲线y f(x)的切线 81 B．若 f(x)有三个不同的零点x,x ,x ，则x x x  1 2 3 1 2 3 2 C．存在a,b，使得xb为曲线y f(x)的对称轴 a D．当x  时， f x在xx 处的切线与函数y f x的图象有且仅有两个交点 0 2 0 43．（多选题）（湖北省新八校协作体2023-2024学年高三10月联考数学试题）设函数 f x的定义域为R，  π f x 为奇函数， f xπ为偶函数．当x0,π时， f xcosx，则下列结论正确的有（ ）  2 7π A． f x在3π,4π上单调递减 B． f  0  2   5  C．点 π,0是函数 f x的一个对称中心 D．方程 f xlgx0有5个实数解  2  44．（多选题）（湖北省新八校协作体2023-2024学年高三10月联考数学试题） 表示不超过x的最大整数， 例如，[0.5]1， 1.1 1，已知函数 f x x ，下列结论正确的有（ ） 1  1 A．若x0,1，则 f x   f x  4  4 B． f xy f x f y C．设gx f  2 5x   f   x2  ，则 20 gk401 20 k1   14 40 D．所有满足 f m fn m,n  0, 的点m,n组成的区域的面积和为   3  9 45．（多选题）（河南省七校联考2024届高三第二次联合教学质量检测数学试题）已知函数 f x的定义域 为R，且满足 f x f y f x y2xy1, f 13，则下列结论正确的是（ ） A． f 421 B．方程 f xx有整数解 C． f x1是偶函数 D． f x1是偶函数 46．（多选题）（河南省七校联考2024届高三第二次联合教学质量检测数学试题）如图，在长方体 1 ABCDABCD中，ABBC2，AA4，N 为棱CD中点，DM  ，P为线段AB上一动点，下列结 2 论正确的是（ ） 学科网（北京）股份有限公司6 5 A．线段DP长度的最小值为 5 B．存在点P，使APPC 2 3 C．存在点P，使AC平面MNP 17 D．以B为球心， 为半径的球体被平面ABC所截的截面面积为6π 6 47．（多选题）（河南省部分名校2023-2024学年高三阶段性测试（二）数学试题）已知函数 1 f(x)sin2x ，则（ ） sinxcosx A． f(x)为奇函数 B． f(x)的值域为(,2 2][2 2,) 3π C． f(x)的图象关于直线x 对称 4 D． f(x)以π为周期 48．（多选题）（河南省部分名校2023-2024学年高三阶段性测试（二）数学试题）已知对任意x0，不等 式exax32ax2lnx0恒成立，则实数a的可能取值为（ ） e A．1 B． C．e D．e2 2 1 49．（多选题）（河南省部分名校2023-2024学年高三10月月考数学试卷）已知函数 f x 1，则下列 lnx 说法正确的是（ ） A． f x的图象无对称中心 1 B． f x f   2 x 1 C． f x的图象与gx 1的图象关于原点对称 lnx D． f x的图象与hxex1的图象关于直线y x对称 101 50．（多选题）（河南省部分名校2023-2024学年高三10月月考数学试卷）记函数 f xex  的零点为x ， x 0 则下列说法正确的是（ ） A．x lnx 0 0 0 1 3 B．x  ,  0 2 4 3 C．当x 时， f x x1 2 1 D．x 0 为函数 gx ex xlnx的极值点 x1 51．（多选题）（河南省部分名校2024届高三月考（一）数学试题）已知定义在实数集R上的函数 f x， 1 其导函数为 fx，且满足 f x y f x f yxy， f 10, f1 ，则（ ） 2 A． f x的图像关于点1,0成中心对称 3 B． f2 2 C． f 202410122023 2024 D．  f(k)10122024 k1 π 52．（多选题）（河南省部分名校2024届高三月考（一）数学试题）设函数 f(x)的定义域为R， f(x )为 4 π π π 4 奇函数， f(x )为偶函数，当x( , ]时， f(x)cos x，则（ ） 4 4 4 3 3π A． f(x4π) f(x) B． f(x)的图象关于直线x 对称 4 3π C． f(x)在区间( ,2π)上为增函数 D．方程 f(x)lgx0仅有4个实数解 2 53．（广东省五校2023-2024学年高三10月联考（二）数学试题）已知函数 f(x)的定义域为(0,)，其导 函数为 f(x)，若xf(x)10. f(e)2，则关于x的不等式 f(ex) x1的解集为 . 54．（广东省七校2024届高三第二次联考数学试卷）已知函数 f(x) 3x1 ，数列a 满足a 1，a 2， 3x1 n 1 2 a a  nN* ， f a  f a a 0，则 2  024 a  . n3 n 2 3 4 i i1  π 55．（广东省七校2024届高三第二次联考数学试卷）函数 f x8lnsinxsin22x在区间0, 上的零点个  2 数为 个． 学科网（北京）股份有限公司56．（广东省（上进联考）2024届高三10月阶段检测考数学试题）已知正数a,b满足2a1b14，则ab 的最小值为 ． sinacos cos3 57．（广东省（上进联考）2024届高三10月阶段检测考数学试题）若关于的方程  在 cosasin sin3  π 区间0, 上有且仅有一个实数解，则实数a ．  4 x2 y2 58．（广东省顺德区高中第四联盟2023-2024学年高三10月联考数学试卷）椭圆  1ab0的离 a2 b2 51 x2 y2 心率e满足e ，则称该椭圆为“黄金椭圆”．若  110m0是“黄金椭圆”，则m ； 2 10 m “黄金椭圆”C: x2  y2 1ab0两个焦点分别为Fc,0、F c,0（c0），P为椭圆C上的异于顶点 a2 b2 1 2 PM 的任意一点，点M是PFF 的内心，连接PM并延长交FF 于N，则  ． 1 2 1 2 MN 59．（广东省肇庆市肇庆中学2024届高三10月月考数学试卷）若存在实数t，对任意的x∈(0，s]，不等式(lnx －x＋2－t)(1－t－x)≤0成立，则整数s的最大值为 ．(ln3≈1.099，ln4≈1.386) 60．（湖南省长沙市雅礼中学2024届高三月考（二）数学试题）如图，VABC中，AB6，AC2BC，D 为AB中点，则tanBDC的取值范围为 . 61．（湖南省长沙市雅礼中学2024届高三月考（二）数学试题）小军和小方两人先后在装有若干黑球的黑 盒子与装有若干白球的白盒子（黑球数少于白球数）轮流取球，规定每次取球可以从某一盒子中取出任意 多颗（至少取1颗），或者在两个盒子中取出相同颗数的球（至少各取1颗），最后不能按规则取的人输.已知 两盒中共有11个球，且两人掷硬币后决定由小军先手取球.小方看了眼黑盒中的球，对小军说：“你输了！” 若已知小方有必胜策略，则黑盒中球数为 . 62．（湖南省长沙市长郡中学2024届高三月考（二）数学试卷）小澄玩一个游戏：一开始她在2个盒子A,B 中分别放入3颗糖，然后在游戏的每一轮她投掷一个质地均匀的骰子，如果结果小于3她就将B中的1颗糖 放入A中，否则将A中的1颗糖放入B中，直到无法继续游戏．那么游戏结束时B中没有糖的概率 是 ． 63．（湖北省云学部分重点高中联盟2023-2024学年高三10月联考数学试卷）在如图所示的直角梯形ABCD 12   中，AB∥CD,AB1,BCCD2,ABBC.P为梯形ABCD内一动点，且AP1，若APABAD，则   的最大值为 . 2 64．（湖北省武汉外国语学校2023-2024学年高三10月月考数学试题）掷一个质地均匀的骰子，向上的点数 不小于3得2分，向上的点数小于3得1分，反复掷这个骰子，（1）恰好得3分的概率为 ；（2） 恰好得n分的概率为 ．（用与n有关的式子作答） 65．（湖北省新八校协作体2023-2024学年高三10月联考数学试题）任意一个三次多项式函数 f xax3bx2cxd的图象都有且仅有一个中心对称点为  x，f x  ，其中x 是 的根， 0 0 0 ″ ″ =0 是 的导数.若函数 f xx3 px2xq图象的中心对称点为1，2，存在x1,，使得 ' ex mxelnx1  f xx33x2e  xe成立，则m的取值范围为 . 66．（河南省七校联考2024届高三第二次联合教学质量检测数学试题）南宋数学家杨辉为我国古代数学研 究做出了杰出贡献，他的著名研究成果“杨辉三角”记录于其重要著作《详解九章算法》，该著作中的“垛积术” 问题介绍了高阶等差数列，以高阶等差数列中的二阶等差数列为例，其特点是从数列的第二项开始，每一 项与前一项的差构成等差数列.若某个二阶等差数列的前4项为1，3，7，13，则该数列的第15项为 ． 67．（河南省七校联考2024届高三第二次联合教学质量检测数学试题）在平面直角坐标系xOy中，A、B分 别为x、y轴上的点，2OA  OB ，则以原点为顶点且经过A、B两点的抛物线的准线斜率为 . 68．（河南省部分名校2023-2024学年高三阶段性测试（二）数学试题）已知a,b均为正实数，且2a3bab， 1 3 则  的最小值为 . a3 b2 69．（河南省部分名校2023-2024学年高三阶段性测试（二）数学试题）已知曲线yex上有不同的两点P和 Q，若点P,Q关于直线y x的对称点P,Q在曲线y=kx2-x上，则实数k的取值范围为 . 70．（河南省部分名校2023-2024学年高三10月月考数学试卷）若函数 f xsinxax的图象上存在A,B两 π 点使得 f x在A处的切线与在B处的切线的夹角为 ，则实数a的取值范围是 . 4 学科网（北京）股份有限公司a2b2 71．（河南省部分名校2023-2024学年高三10月月考数学试卷）已知ab0，则 的最小值为 . abb2 x2 y2 72．（河南省部分名校2024届高三月考（一）数学试题）已知双曲线  1(a,b0)的左焦点为F ，过 a2 b2   2π 坐标原点O作直线与双曲线的左右两支分别交于A,B两点，且 FB 4FA,AFB ，则双曲线的渐近线 3 方程为 ． 14